Opgave: Eulerlinjen

Den linje, der går gennem midtnormalernes, højdernes og medianernes skæringspunkter i en vilkårlig trekant, kaldes Eulerlinjen.

Du skal tegne Eulerlinjen i GeoGebra og undersøge disse fire påstande:

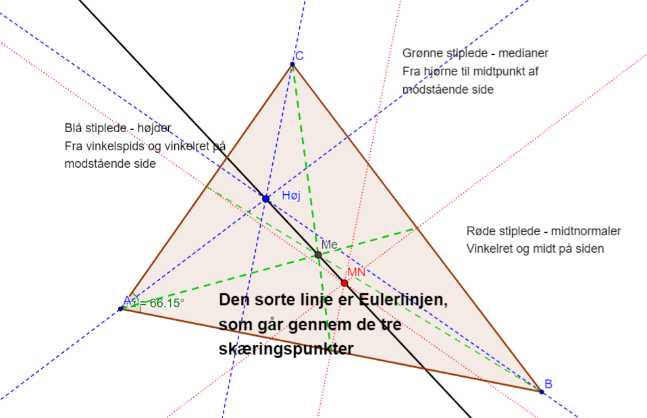
1. Eulerlinjen kan kun tegnes i spidsvinklede trekanter.
2. Det kan ske, at de tre punkter, der definerer Eulerlinjen, falder sammen i et punkt.
3. Vinkel ­halverings­ linjens skæringspunkt ligger også på Eulerlinjen.
4. Der er et fast forhold mellem de linjestykker på Eulerlinjen, der afgrænses af midt­normalernes, højdernes og medianernes skæringspunkter.

Resultaterne af undersøgelserne skal dokumenteres ved hjælp af skærmbilleder med tilhørende forklaringer eller ved et screencast, der viser hele processen.

Eulerlinjen kan også hentes som applet på GeogebraTube.

Konstrueret episode, hvor to elever arbejder i GeoGebra med påstandene omkring Eulerlinjen:

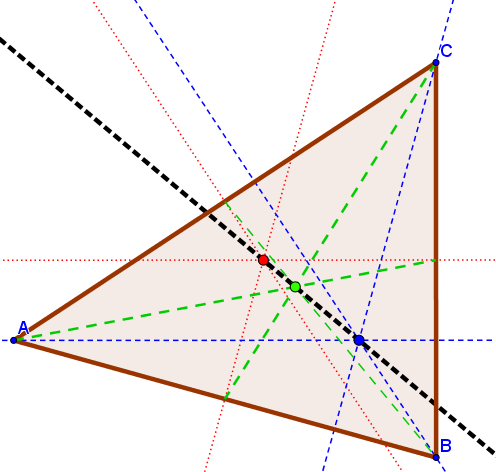
Jesper: "Nu har vi tegnet trekanten og de tre slags linjer i GeoGebra. Vi har givet dem forskellige farver, så højderne er blå, medianerne grønne og midtnormalerne røde."

Katrine: "Det ser ud som om, at lige meget hvordan jeg trækker i hjørnerne, bliver skæringspunkterne ved med at ligge på den samme stiplede linje?"                               

Jesper: "Hvad hvis nu vi gør en af vinklerne rette?"

Katrine: "Så falder højdernes skæringspunkt sammen med punktet med den rette vinkel – men det gør de to andre ikke?"

Jesper: "Kan vi mon få dem alle sammen til at ligge oven i hinanden?"

Læreren: "Det ser rigtig godt ud. I har fået lavet en figur, der er dynamisk, så I kan undersøge trekantens linjer og deres skæringspunkter. Men hvad med vinkelhalveringslinjen – den er jo også en af trekantens linjer?"

Jesper: "Vi har prøvet at tegne to af dem, men det ser ud som om, de falder ved siden af?"

Læreren: "Ja?"

Katrine: "Men måske kan vi få det til at passe, hvis vi trækker i hjørnerne?"

Læreren: "Hvad tænker I der skal til, for at de falder sammen – alle tre eller alle fire slags linjer?"

Fællesgørelse

Læreren kan fx vælge at lade et par elever gennemgå deres løsningsforslag for hele klassen med en elevstyret gennemgang og diskussion.