Instrumentel orkestrering

Begrebet instrumentel orkestrering beskriver lærerens systematiske organisering af en undervisningssituation, hvor det digitale værktøj og den matematiske viden begge betragtes som instrumenter til læring. Formålet med at arbejde med instrumentel orkestrering i matematikundervisningen er at støtte, vejlede og udvikle elevernes brug af udvalgte digitale værktøjer. Læs om begrebet og om scenarier, hvor den instrumentelle orkestrering kan udfoldes.

1. udvælger digitale værktøjer til den aktuelle undervisningssituation,
2. tager beslutning om, hvordan det digitale værktøj præsenteres og udnyttes og
3. er parat til at justere forløbet undervejs i forhold til opståede spørgsmål – enten af matematisk karakter eller hvad angår brug og funktion af værktøjet.

Et konkret eksempel på denne proces kan fx ses i Eulerlinjen, hvor læreren har valgt GeoGebra som det digitale værktøj, der skal sættes i spil. Læreren har taget stilling til, om eleverne selv skal konstruere Eulerlinjen i en vilkårlig trekant, eller om de kan arbejde med den konstruktion, der er lagt ud til dem. Afhængigt af elevernes reaktioner på opgaven kan læreren justere på det planlagte forløb – enten for at behandle nogle af de matematiske begreber eller for at sikre sig, at trekant og linjer er konstruerede, så de leder frem mod den ønskede matematiske indsigt.

Instrumentel orkestrering

Begrebet orchestration instrumentale dækker over matematiklærerens systematiske organisering af en undervisningssituation. (Kilde 1)

Formålet med begrebet er at støtte, vejlede og udvikle elevernes brug af udvalgte digitale værktøjer.
Ordet instrument har her også en særlig betydning. Det skal her opfattes som kombinationen af værktøj og matematisk viden. At understøtte elevernes udvikling af et instrument er derfor relateret til både matematik og til brug af værktøjet.

Bemærk, at lærere og elever på den måde har hver deres eget instrument. Instrumentel orkestrering drejer sig altså om at få eleverne til at 'spille hensigtsmæssigt' – og det er lærerens opgave og ansvar at facilitere det.

Fællesgørelsen ved instrumentel orkestrering

I en undervisningssituation skal læreren beslutte hvilke værktøjer, der skal være mulige at anvende for eleverne i sammenhæng med den matematiske problemstilling. Det kan ske på baggrund af overvejelser om, hvordan de enkelte værktøjer kan bidrage til løsning af særlige opgaver, samt hvordan den instrumentelle orkestrering skal organiseres.

Seks forskellige scenarier for den instrumentelle orkestrering:

• I. Teknisk demonstration
  Læreren demonstrerer, hvordan det digitale værktøj skal anvendes for hele klassen på den fælles skærm.
• II. Fælles faglig demonstration
  Læreren forklarer, hvordan en opgave kan løses for hele klassen samlet på den fælles skærm.
• III. Skærm/tavledemonstration
  Læreren demonstrerer og understreger sammenhængen mellem de digitale løsningsmuligheder i en opgave på skærmen og de mere traditionelle på tavlen.
• IV. Fælles diskussion
  Læreren styrer en klassesamtale, hvor målet er at opnå en fælles viden og forståelse for de digitale aktioner, der foregår på den fælles skærm.
• V. Elevbesvarelse til diskussion
  Læreren bringer en elevs aktuelle løsningsforslag til fælles diskussion i klassen på den fælles skærm.
• VI. Elevstyret gennemgang og diskussion
  Styringen af løsningsforslag overlades til en af eleverne og er synlig for hele klassen på den fælles skærm i den fælles diskussion. (Kilde 1)  

I de tre første scenarier er det læreren, der styrer og bestemmer både indhold og måden, det digitale værktøj bringes i anvendelse på, mens eleverne i de tre efterfølgende scenarier inddrages stadig mere.

Værktøjets begrænsninger

Værktøjets begrænsninger er vigtige af have for øje i instrumentel orkestrering. De digitale matematikværktøjer kan have begrænsninger, fx i forhold til hvor godt de kan repræsentere matematiske objekter eller løse bestemte matematikopgaver.

Undertiden kan værktøjerne endda give svar, som eleverne ikke umiddelbart forstår, eller værktøjerne kan lave direkte misvisende repræsentationer. Det er altså vigtigt, at læreren både kender værktøjets muligheder og værktøjets begrænsninger og bruger sin viden om det til at lade eleverne erfare netop mulighederne og begrænsningerne. Det vil dels gøre elevens brug af værktøjer mere sikker, og dels hjælpe eleven med at undgå blind autoritetstro i forhold til det, som værktøjet producerer.

Udover værktøjets begrænsninger kan de svar, som de digitale værktøjer giver, også være vanskelige at afkode for nogle elever.

I dette eksempel er det fx vigtigt, at eleverne er fortrolige med det aktuelle programs syntakser og udtryk:

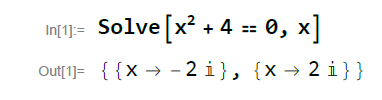
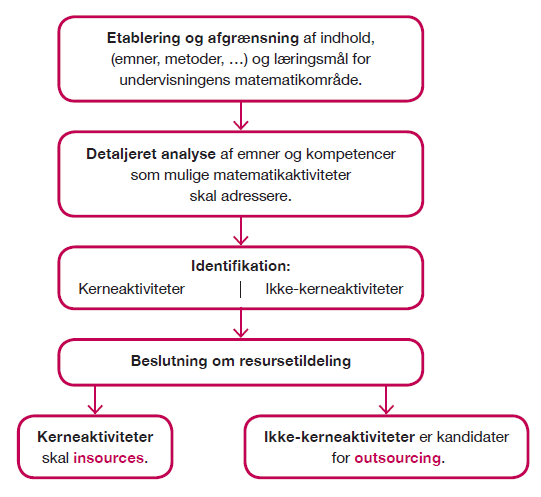
Insourcing eller outsourcing – en model

I en artikel: 'Matematik med it' præsenteres overvejelserne omkring en opgave som indgang til at formulere den generelle problematik, om aktiviteten skal insources eller outsources – om det, der skal læres, skal opnås med matematik-interne ressourcer, eller om det kan eller skal overlades til digitale værktøjer. (Kilde 2) 

De digitale værktøjer fungerer som udgangspunkt ikke af sig selv, men repræsenterer en række muligheder, som brugeren kan sætte i spil i forbindelse med at løse en opgave eller arbejde med en problemstilling.

I artiklen anvendes en metafor for underviseren som en virksomhedsleder, der har ansvaret for, om de enkelte matematiske aktiviteter er af en karakter, som kan overlades til såkaldt eksterne aktører – her digitale værktøjer, – eller om aktiviteten er så vigtig for læringsprocessen, at den skal holdes inden for virksomhedens egne rammer. Det er der selvsagt ikke endegyldige svar på, men det er afgørende vigtigt, at underviseren foretager sig disse overvejelser.

Når digitale værktøjer anvendes til at løse matematiske problemer indgår de ofte som erstatning for mere klassiske matematiske aktiviteter som fx håndtegning af figurer eller løsning af ligninger i hånden. Ofte vælges digitale værktøjer, fordi de er hurtigere og mere effektive. Men i undervisningsmæssige sammenhænge kan det være vigtigere, hvad man kan lære af en løsningsmetode. Her skal underviseren være opmærksom på, at den viden, som en mere klassisk metode kræver eller udvikler, ikke automatisk følger med, når man bruger et digitalt værktøj.

Instrumentel orkestrering handler derfor også om at styre brugen af værktøjer sådan, at eleverne ikke bare bliver i stand til at løse opgaver hurtigt og effektivt, men også opnår indsigt i betydningen af og begrundelsen for de matematiske metoder og objekter, som indgår.

Det kan bl.a. ske gennem bevidst og varieret brug af insourcing og outsourcing.
Hvis målet er, at eleverne skal opdage eller konsolidere regler vedrørende ligningsløsning, så vil det være oplagt at insource, mens det vil være oplagt at outsource ligningsløsningen til et digitalt værktøj, hvis de arbejder med fx Regnmåleren, hvor ligningsløsning er den del af problemløsningen.

Opgaver, der inkluderer digitale værktøjer som en væsentlig faktor i arbejdet med problemløsning, kan hjælpe eleverne til at forstå værdien af at anvende digitale værktøjer i matematikundervisningen.

Det er derfor også lærerens opgave at vurdere elevernes digitale kompetencer sammen med deres matematiske viden, og netop det kan være en udfordring pga. den komplekse relation mellem værktøj og matematik.

Denne kompleksitet kan der arbejdes med i undervisningssituationer med forskellige fokuspunkter. Hvert fokuspunkt indeholder et konkret eksempel, som hver relaterer til en mulig undervisningssituation, hvor et eller flere af de seks scenarier af orkestreringer kan sættes i spil.  

Se de 6 opgaver med forskellige fokuspunkter.