Hvad er mønster og symmetri?
I dette tema vil vi fokusere på, hvad vi i matematik forstår ved mønster og symmetri. Vi vil også give eksempler på, hvordan vi kan give børn i børnehaven erfaringer med mønster og symmetri gennem matematiske aktiviteter.
Forskellige mønstre findes overalt i vores omgivelser. Vi kan fx finde forskellige mønstre i arkitektur, tæpper, duge, tøj, kunst og naturen. I matematik er det interessant at klassificere forskellige mønstre, der findes i miljøet – både naturlige og menneskeskabte. Vi har f.eks. både numeriske mønstre og geometriske mønstre. Talmønstre kan være 1, 3, 5, ... og 2, 4, 6, ..., men i dette tema vil vi fokusere på geometriske mønstre.
Gentagelser og rækkefølge
Vi kan lave et mønster på mange måder. To vigtige begreber, der er relateret til og kan beskrive et mønster, er gentagelse og rækkefølge. Når vi vil tale om et mønster – uanset om det er med børn eller voksne – på et billede, en bygning, en børnetegning eller en blomst, skal vi tale om, at der er noget, der går igen eller gentager sig i en bestemt rækkefølge. Hvis det er et geometrisk mønster, vi ønsker at tale om, vil dette mønster indeholde en geometrisk form eller flere geometriske former, der gentager sig selv i en bestemt rækkefølge. Det er netop denne gentagelse og rækkefølge, der også danner grundlaget for det, vi kalder et mønster eller et gentagende mønster (Kilde 2). Der er meget forskning om sådanne gentagende mønstre i matematikundervisningen. Sådanne gentagende mønstre hævdes at være vigtige i matematik og for børns første rejse ind i matematikkens verden. De er særligt vigtige, da de kan danne udgangspunkt for læring om generalisering – en central proces i matematik. Læs mere om udviklingen af børns forståelse for mønstre i teksten ”Børns udvikling af forståelse for mønstre”.

Eksempler på gentagende mønstre kan være hvide og røde legoklodser, en rød - en hvid - en rød - en hvid osv. Et andet eksempel kunne være et klap - to tramp - et klap - to tramp osv. Et tredje eksempel kunne være, at børnene selv laver mønstre ved hjælp af ting fra naturen.
Aktiviteter med mønstre i børnehaven

Her ser vi et eksempel på en aktivitet, som fint kan bruges i en børnehave. I en samtale med børnene kan vi spørge:
- Hvordan er mønstret i de forskellige rækker bygget op?
- Kan I prøve at fortælle, hvad I ser?
Mønsteret er ganske enkelt lavet ved hjælp af fire forskellige ting fra naturen: sten, kogler, pinde og blade. På billedet kan vi se, at der er lavet tre mønstre. Dette er kun nogle ganske få af de mønstre, som det er muligt at lave med de fire ting.
Vi kan se, at mønstrene dannes på følgende måde:
Første række: 1 kogle | 1 blad | 1 pind | 1 sten | 1 kogle | 1 blad | 1 pind | 1 sten osv.
Anden række: 2 kogler | 1 sten | 1 pind | 2 blade | 2 kogler | 1 sten | 1 pind | 2 blade osv.
Tredje række: 1 blad | 2 pinde | 3 sten | 4 kogler | 1 blad | 2 pinde | 3 sten | 4 kogler osv.
Det er disse "og så videre", der er en del af hemmeligheden ved mønstre. Vi skal tale med børnene om, at vi kan se for os, hvordan mønsteret fortsætter på denne måde. Forskellige mønstre kan således være gode udgangspunkter for matematiske samtaler med børn. Et mere generelt spørgsmål, man som pædagog kan stille sig selv, er: Hvordan kan vi arbejde med sådanne og lignende mønstre i børnehaven?
I børnehaven kan en aktivitet med at lave mønstre med ting fra naturen være aktuelt på en turdag, afhængigt af børnehavens udeområde. Som pædagog kan du bede børnene om at finde et bestemt antal sten, kogler, pinde og blade og derefter lade dem prøve at lave mønstre selv. Børnenes forskellige mønstre bliver så et grundlag for en matematisk samtale med børnene, hvor nogen kan fortælle, hvordan mønstret er opbygget. Det barn, der har lavet mønsteret, kan så afgøre, om de andre børn har opdaget mønsteret. Som pædagog kan du flette begreberne gentagelse og rækkefølge ind, så børnene får mulighed for at tilegne sig dem og bruge dem i deres egne fortællinger om mønsteret. En sådan aktivitet kan udvides ved at bruge fx muslingeskaller og/eller græsstrå. Læs flere eksempler på aktiviteter i teksten ’Aktiviteter og lege’.
Forskellige typer mønstre
I matematikken opdeler vi mønstre i to forskellige typer af afbildninger:
- formbevarende afbildninger, hvor formen, men ikke nødvendigvis størrelses, bevares. Det kan være ved at forstørre og formindske.
- kongruensafbildninger, hvor både form og størrelse bevares. Det kan være ved at dreje, spejle og parallelforskyde.
En afbildning er en proces, hvor en "grundform" ændres/flyttes. Resultatet kaldes "billedet". Hvis vi ser på os selv i et almindeligt spejl, er vores ansigt grundformen, og spejlbilledet bliver til billedet.
Der er mange forskellige måder, hvorpå børn kan få erfaringer med mønstre, både de formbevarende og de kongruensbevarende. Det er jo faktisk sådan, at hvis børn går rundt med en lup og kigger efter insekter i naturen eller bruger en kikkert til at se på fugle, så får de erfaring med forstørrelse. På samme måde kan børn opleve formbevarende afbildninger, når de zoomer ind på en mobiltelefon ved at "trække billedet ud” med fingrene, dvs. forstørre, og formindske ved at zoome ud ved at "trække billedet sammen” med fingrene.
I dette tema fokuserer vi på kongruensafbildninger. Hvis mønsteret er lavet på en speciel måde ud fra kongruensafbildninger, siger vi i matematik, at mønsteret er symmetrisk. Begrebet symmetri er tæt knyttet til mønsteret, fordi opbygningen af mønstret i nogle tilfælde kan beskrives ved hjælp af forskellige symmetrier (Kilde 3). I en strikket uldtrøje kan vi fx ofte se eksempler på spejlingssymmetri og parallelforskydningssymmetri.
Drejning, spejling og parallelforskydning
I matematik deler vi begrebet symmetri op i tre forskellige symmetrier, nemlig drejning, spejling og parallelforskydning. Børn i børnehaven kan få erfaringer med alle tre.
Spejling
Figuren spejles i en spejlingsakse.

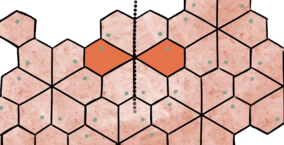
Drejning
Figuren drejes omkring et punkt.

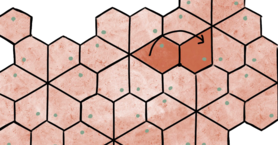
Parallelforskydning
Figuren flyttes en bestemt afstand i en given retning.
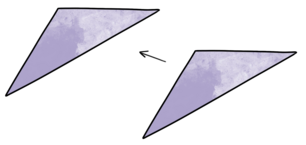
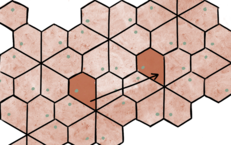
Drejningssymmetri kan opleves i vindmøller og svingdøre. Det er noget, der kører rundt. Kan noget drejes (vendes rundt), så det bagefter ser ud på samme måde, som før det blev drejet? Se på en blomst med fire kronblade (se også filmen "Malthes solsikke"). Hvis vi drejer den en kvart omgang, ser den ud, som da vi begyndte. Solsikkefrøene sidder i spiraler, så de danner et mønster med drejningssymmetri. Du kan også folde et ark papir, klippe nogle huller i det og derefter folde arket ud igen. Du kan tale med børn om det mønster, der opstår: Kan du dreje papiret nogle gange, så det ser ud på samme måde bagefter? Matematisk set er drejningssymmetri entydigt bestemt af mønsterets drejningscentrum og drejningsvinklen (hvor meget man drejer).
Spejlingssymmetri er entydigt bestemt af dens spejlingslinje. Børn kan få erfaringer med spejling ved at tegne en streg på et stykke papir og lave en tegning på den ene side af stregen. Hvordan vil tegningen på den anden side se ud, når den er spejlet? Børn kan også være hinandens spejlbilleder. Det ene barn spejler sig selv (grundformen), og det andet barn er spejlbilledet (billedet), som skal gøre nøjagtig det samme som det barn, der spejles. Spejlingssymmetri kan også findes i naturen og inde i børnehaven.
Parallelforskydning kan vi se på et tapetmønster eller en dug. En parallelforskydningssymmetri er entydigt bestemt af den retning, vi bevæger grundformen, og hvor langt vi bevæger den. Tre børn kan stå på gulvet med armene udstrakt, så de rører hinanden og danner en trekant. Så kan børnene få til opgave at flytte sig med fem museskridt hen mod vinduet. Når de har gjort det, er trekanten den samme (samme form og størrelse), men den er blevet flyttet.
Hvis man spejler, drejer og/eller parallelforskyder en eller flere figurer på en måde, så de kan dække en flade uden at overlappe hinanden eller ’lave huller’, kalder vi det for tesselering. Se eksempler på det i teksten 'Flisemønstre'.
Til overvejelse i teamet
- Hvilke eksempler har vi på, at børn laver mønstre i børnehaven?
- På hvilke måder er vi opmærksomme på, hvordan vi taler med børnene om de erfaringer, de gør sig?
- På hvilke måder kan vi tilrettelægge situationer, hvor børn kan gøre sig (yderligere) erfaringer med mønstre i dagligdagssituationer og i planlagte, styrede aktiviteter?
til: DAGTILBUD
emne: MØNSTRE OG SYMMETRIER
UDGIVET: 2023
Forfatter
Martin Carlsen
Professor
Institutt for matematiske fag, UiA
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Carlsen, M., Wathne, U., & Blomgren, G. (2017). Matematikk for barnehagelærere (3. utg). Oslo: Cappelen Damm Akademisk.
- Clements, D. H. & Sarama, J. (2014): Learning and teaching early math. The learning trajectories approach (2. utg.). New York og London: Routledge.
- Størksen, I., ten Braak, D., Breive, S., Lenes, R., Lunde, S., Carlsen, M., Erfjord, I., Hundeland, P. S., & Rege, M. (2018). Lekbasert læring – et forskningsbasert førskoleopplegg fra Agderprosjektet. Oslo: Gan Aschehoug.