Hvorfor er funktionsbegrebet så svært?
Det er der mange grunde til! Vi ser her på nogle af de årsager til læringsvanskeligheder ved funktioner, som er belyst i forskningen. Det drejer sig især om følgende fire generelle forhold, som også gør sig gældende inden for andre områder af matematikken.
For det første kræver det algebraisk indsigt at fortolke og arbejde med funktionsudtryk. Elever, der ikke mestrer algebra på det givne niveau, kan derfor have svært ved funktioner.
For det andet spiller de forskellige repræsentationer og navnlig forbindelserne mellem dem en hovedrolle i arbejdet med funktioner. Repræsentation af funktioner sprogligt, som tabel, symbolsk algebraisk og som grafer - samt omformning og skift imellem dem kan volde eleverne vanskeligheder. Det er nærmere belyst i: Hvordan kan man arbejde med funktionsbegrebet?
For det tredje vil de eksempler på funktioner, som eleverne især arbejder med på de forskellige trin i uddannelsessystemet, ikke altid udspænde begrebet i forhold til, hvordan en funktion defineres på det pågældende trin. Fra forskning ved man, at eleverne skaber mentale billeder, såkaldte begrebsbilleder, af de matematiske begreber ud fra, hvordan begrebet optræder i de konkrete eksempler, de arbejder med. Elevernes begrebsbilleder stemmer derfor ikke altid overens med de definitioner af begrebet, som de er blevet præsenteret for i deres matematikundervisning. En uoverensstemmelse mellem begrebsdefinitioner og begrebsbilleder kan føre til matematikvanskeligheder. Ydermere kan elevernes begrebsbilleder rumme selvmodsigelser, som eleven først bliver klar over, hvis disse aktiveres samtidig i konkrete sammenhænge. Begge dele kan man læse mere om i afsnittet Begrebsdefinitioner og begrebsbilleder (Kilde 1).
For det fjerde er der ved mange matematiske begreber og specielt ved funktionsbegrebet en grundlæggende dobbelthed (dualitet) mellem forståelse af begrebet som en proces og som et objekt – funktionen opfattet som en ting i sig selv. Det kan man læse om i temaet Algebra på tværs. Proces-objekt-dualiteten er fremtrædende ved funktionsbegrebet og giver ofte anledning til læringsvanskeligheder. Til at begynde med arbejder man med funktioner som en proces, men på et tidspunkt er det nødvendigt også at kunne forstå en funktion som et objekt - noget som man kan karakterisere og gøre noget ved (Kilde 2). Det ses der nærmere på i afsnittet Proces- og objektdualiteten.
Det matematiske begreb og dets repræsentationer
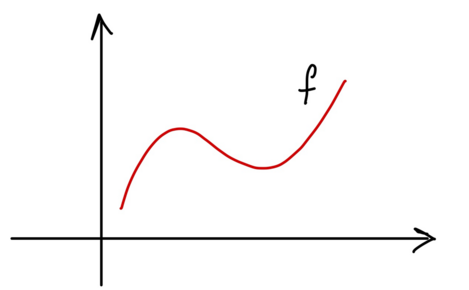
At forstå og at skabe mening i et begreb er tæt forbundet med de repræsentationer af begrebet, som man har mødt og arbejdet med (Kilde 3). Det kan være fristende, at man som lærer ofte benytter en ”standardfunktion”, som fx en lineær funktion eller funktionen vist på figur 1, når man taler med sine elever om funktioner og deres egenskaber. Men det kan gøre det svært for eleverne at se, at alle graferne på figur 2 viser funktioner. Med andre ord: Det er af stor betydning, at eleverne møder et bredt udvalg af funktioner, for at få en bred forståelse af begrebet. Ligeledes er det vigtigt, at de forholder sig til ikke-eksempler, der ved første øjekast, men ikke ved nærmere eftersyn, er graf for funktioner, som i figur 2b.
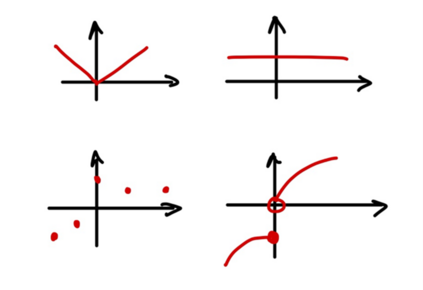
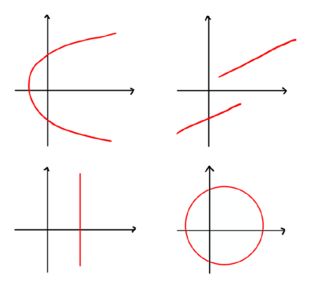
Elever skaber mening i abstrakte begreber som f.eks. funktionsbegrebet gennem aktivitet: opgaveregning, problemløsning, undersøgelser og modellering. Under aktiviteten arbejdes med forskellige aspekter af det abstrakte begreb blandt andet ved at benytte forskellige repræsentationer, og her er det vigtigt at skelne mellem repræsentation og begreb. Repræsentationerne er ikke begrebet, men de er en måde at tilgå det på (Kilde 4).
Den epistemologiske trekant er en didaktisk model, som også kan belyse funktionsbegrebet.
På figur 3 ses en model for relationen mellem den matematiske genstand (objektet) og den kontekst den lever i, de symboler man bruger til at beskrive objektet med og det bagvedliggende abstrakte begreb (Kilde 5). Man kalder modellen for den epistemologiske trekant, og den kan anvendes på alle matematiske begreber.
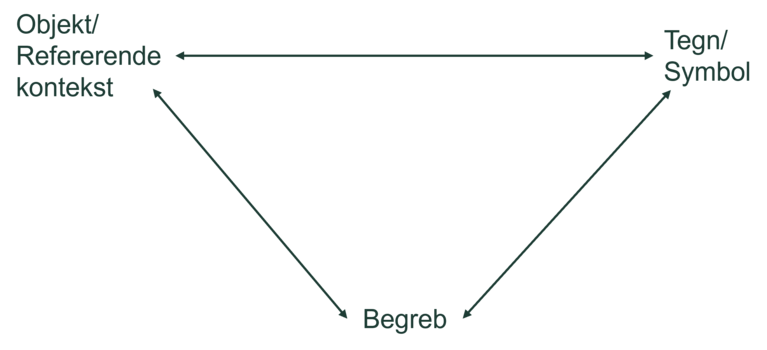
I eksemplet med Ella og Klara i brusebadet arbejder man med at skabe mening i, hvordan man kan lave nye funktioner ved at lægge allerede kendte funktioner sammen ved hjælp af funktionsgrafer. Dette kan anskueliggøres med en epistemologisk trekant som vist på figur 4.
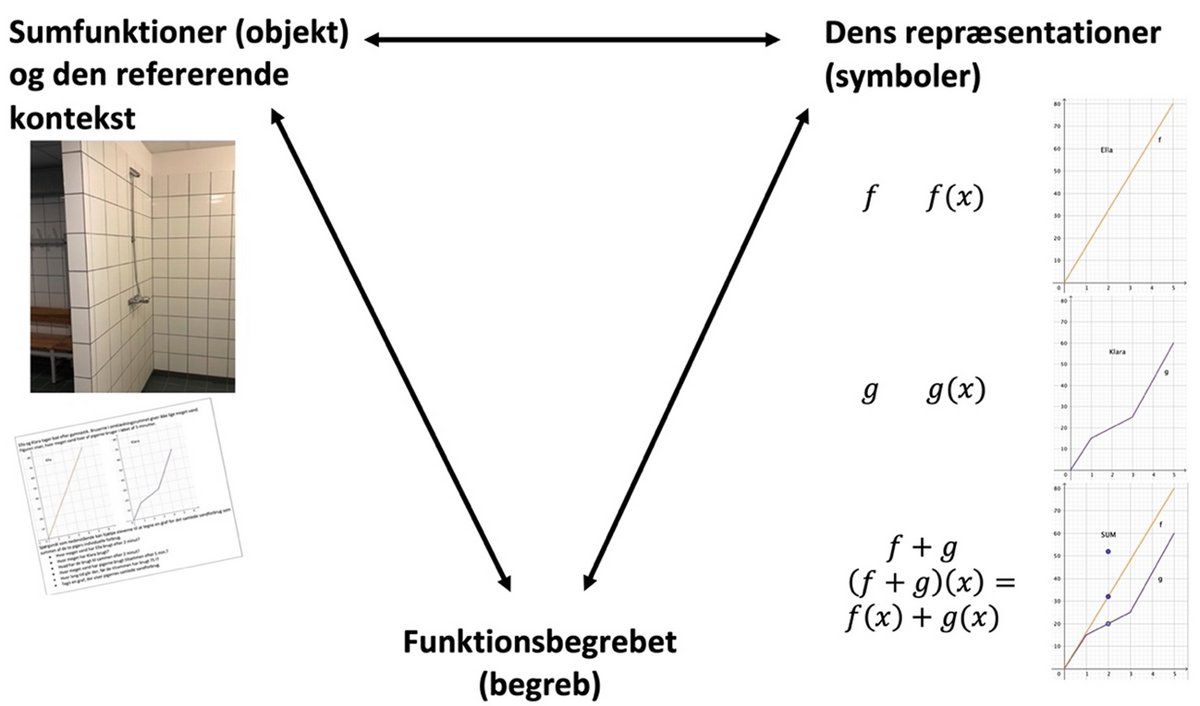
For at lære om sumfunktioner og skabe mening i den tilhørende algebraiske notation, arbejder eleverne med en helt konkret kontekst, et brusebad efter en gymnastiktime. Den mængde vand, pigerne Ella og Klara hver især bruger, er beskrevet som en tekst og skal afsættes som grafer i et koordinatsystem, og ud fra graferne kan eleverne uddrage forskellige oplysninger om situationen (den refererende kontekst) og man kan tegne grafen for pigernes samlede vandforbrug. Det samlede vandforbrug, der kan repræsenteres som summen af funktionerne for hver af de to pigers vandforbrug, er den egentlige genstand for aktiviteten. Denne sumfunktion kan få mening i konteksten, og eleverne kan arbejde med at repræsentere den i alle fire former ud fra de tilsvarende repræsentationer af funktionerne for Ella og Klaras vandforbrug.
Relationen mellem genstand og dens repræsentation er angivet som den øverste vandrette dobbeltpil i modellen. Gennem arbejdet med graferne kan funktionen undersøges og forstås. Det abstrakte funktionsbegreb forstås gennem konkrete eksempler som fx funktionen for det samlede vandforbrug, og det er gennem sådanne forskellige eksempler, der etableres viden om begrebet. Dette er vist med den venstre dobbeltpil. Samtidig er det gennem arbejdet med funktionens repræsentationer, at eleverne erkender strukturelle og generelle egenskaber ved begrebet (den højre dobbeltpil).
Hvis man undlader at arbejde med et af de tre hjørner i modellen, eller hvis man identificerer objektet med en af repræsentationerne, vil trekanten kollapse, og eleverne vil ikke opnå den viden og forståelse af begrebet, som er nødvendig.
For at imødegå læringsvanskeligheder, er det vigtigt at arbejde med sammenhængen mellem forskellige repræsentationer. Det betyder, at det er vigtigt at være opmærksom på og italesætte strukturelle egenskaber ved funktioner. Det er ikke tilstrækkeligt ”bare” at regne mange opgaver, hverken i eller uden konkrete kontekster. Og man skal inddrage alle fire repræsentationsformer og ikke blot en enkelt for at give eleverne et bredt funktionsbegreb. Også inden for den enkelte repræsentation skal man tænke på at anvende mange forskellige typer som fx grafer for forskellige funktionstyper vist på figur 1 og figur 2.
I afsnittet Hvordan kan man arbejde med funktionsbegrebet?, kan man se mange eksempler på, hvordan man i undervisningen kan arbejde med at oversætte og veksle mellem forskellige repræsentationer.
Først når man har denne brede forståelse, bliver det muligt at håndtere funktioner som abstrakte genstande eller objekter: ’funktionen, f’, uden som udgangspunkt at kende f nærmere gennem en af de fire repræsentationer. Det har man brug for i gymnasiet og i videregående matematikbaserede uddannelser for at kunne give mening til:
- Den afledte af en differentiabel funktion $f$ er en ny funktion $f'$.
- Ud fra to reelle funktioner $f$ og $g$, som begge er defineret på samme interval, kan man definere en ny funktion $h=f+g$, som er defineret på dette interval med funktionsforskriften $h(x)=f(x)+g(x)$.
- Differentialligninger. For eksempel $f'=f$, funktionen $f$ er løsningen til $f'=f$ og $f(1)=1$.
- To funktioner $f$ og $g$ er ens, $f=g$, hvis de
- har samme input- og outputmængde
- $f(x)=g(x)$ for alle $x$ i inputmængden.
Begrebsdefinitioner og begrebsbilleder
Den forståelse og mening, elever tillægger matematiske begreber, afhænger af de erfaringer, de har gjort sig gennem konkrete oplevelser. Alle de forståelser og opfattelser, en elev får af en funktion gennem problemløsning, modellering osv., og gennem brugen af forskellige repræsentationer, kalder man tilsammen for elevens begrebsbillede. Forskning viser, at uanset hvilken formel definition af en funktion, der undervises i, danner eleverne deres forståelse ud fra de personlige og konkrete erfaringer, de har med funktioner. Derfor kan man heller ikke forvente, at eleverne selvstændigt kan anvende funktionsbegrebet på nye måder og i ukendte situationer (Kilde 1).
Der er tale om et generelt vilkår for tilegnelse af matematiske begreber, som er særlig vigtigt i forbindelse med funktionsbegrebet, fordi det er et grundlæggende og centralt for fortsat matematiklæring og fordi dets betydning udvides mange gange gennem uddannelsessystemet.
En formel definition af funktionsbegrebet som f.eks.:
”En funktion eller en afbildning, kaldet f, er en regel eller forskrift, der til ethvert element x i en mængde A, kaldet definitionsmængden, entydigt bestemmer et element y i en mængde B, kaldet billedmængden; man udtrykker denne entydige sammenhæng ved at skrive $y = f (x)$”
er vigtig ved læring af funktionsbegrebet. Formuleringen og graden af formalisering må naturligvis tilpasses det aktuelle niveau. Den afgørende erkendelse fra matematikdidaktisk forskning er imidlertid, at en sådan definition alene støtter elevernes læring af funktionsbegrebet, hvis den forbindes til elevernes oplevelser og erfaringer med eksempler på funktioner.
Undervejs i læreprocessen danner eleverne sig mange forskellige billeder af, hvad en funktion er og kan være, og det er helt almindeligt, at de kan være fejlagtige, mangelfulde og endda selvmodsigende. Eleven behøver slet ikke at opdage, er der er problemer med nogle af begrebsbillederne, da hun ofte kun vil bruge et enkelt eller få billeder i en given situation. Først i det øjeblik, to begrebsbilleder, der er i modstrid med hinanden, bliver fremkaldt på samme tid, vil eleven opleve eller opdage, at der er et problem. Det er helt almindeligt at elever omkring overgangen mellem grundskole og gymnasie mener, at input til en funktion er de hele tal. Bliver eleven bedt om at finde den værdi af den uafhængige variabel, som resulterer i et bestemt tal, og denne værdi IKKE er et heltal, vil nogle elever reagere ved at mene, at der slet ikke er tale om en funktion, eller der er noget galt med den.
Der findes mange misopfattelser af funktioner. For eksempel mener mange elever at:
- en funktion altid har en forskrift - en ligning, hvor y står på venstre side af lighedstegnet
- en funktion angiver en årsagssammenhæng
- en funktion har en sammenhængende graf.
Man har afdækket forskellige almindelige begrebsbilleder af funktioner (Kilde 6), heriblandt nedenstående.
En funktion er:
- enhver korrespondance mellem to mængder A og B, hvor der for hvert element i A er et og kun et element i B
- en afhængighedsrelation mellem to variable, hvor den ene afhænger af den anden men ikke nødvendigvis efter et bestemt mønster
- en regel, hvor man ved en regel forventer, at noget opfører sig regelmæssigt
- en operation eller en omformning vha. algebraiske operationer
- en formel, en forskrift eller en ligning
- en repræsentation. Ofte identificeres funktionen med dens grafiske eller symbolske repræsentation.
Hvor nogle af disse begrebsbilleder stemmer helt overens med begrebsdefinitionen, er andre mangelfulde eller ligger langt fra denne. En manglende overensstemmelse mellem begrebsdefinitioner og begrebsbilleder resulterer ofte i læringsvanskeligheder.
Hvis eleverne har svage begrebsbilleder, vil de have svært ved at generalisere fra kendte til nye situationer. De vil have vanskeligheder ved at bruge matematikken i ukendte situationer, fx vil Ohms lov $U = R \cdot I$, måske nok ses som en opskrift på at udregne spændingsforskellen ud fra kendskab til modstand og strømstyrke, men ikke som en lineær sammenhæng mellem strømstyrke og spændingsforskel med R konstant, fordi de variable ikke hedder x og y. Tilsvarende vil omskrivningen af Ohms lov til $I = \frac{U}{R}$ opfattes som et helt andet udtryk. Ligeledes kan svage begrebsdefinitioner føre til, at eleverne overgeneraliserer ved f.eks. at lave deres egne regler, såsom at symbolet a altid står for hældningskoefficienten, og derfor også i 2.gradspolynomiet $f(x)=ax^2+bx+c$ angiver hældning. Det er derfor nødvendigt at styrke begrebsdannelsen gennem arbejde med forskellige repræsentationer og at involvere begrebsdefinitionerne i konkrete situationer for at forbinde dem til elevernes begrebsbilleder og dermed tydeliggøre dem.
Proces-objekt-dualiteten
Matematiske begreber som ”tal” og ”funktioner” kan defineres og forstås på to måder (kilde 2): Operationelt, som processer og algoritmer, hvor en handling fører til et resultat, og strukturelt, hvor begrebet er blevet til et statisk objekt, der kan behandles og manipuleres med, og som kan indgå som en del af en anden sammenhæng. Se eksempel her.
I tilfældet med funktioner kan den operationelle forståelse eksemplificeres ved funktionen som en anvisning eller ”opskrift”, hvor funktionsværdierne beregnes et tal ad gangen ved indsættelse i en funktionsforskrift. Denne egenskab er dynamisk. I modsætning hertil kan en funktion også forstås som en statisk struktur f.eks. som en mængde af talpar, der ses som punkter i planen, når man tegner grafen for en funktion. Her opfattes funktionen som et objekt, og denne forståelse er nødvendig, når man for eksempel vil lægge to funktioner sammen, eller man vil differentiere en funktion eller løse en differentialligning. Man skal være opmærksom på, at en funktionsforskrift både kan give anledning til en proces- og en objektforståelse. Benytter man den til at beregne funktionsværdier, fungerer den som proces, men ser man forskriften som en beskrivelse af en bestemt klasse af funktioner med bestemte egenskaber og karakteristika, såsom lineære funktioner, forstås den som objekt.
Eleverne skal i løbet af skolesystemet nå til begge erkendelser og skal kunne betragte og behandle en funktion på begge måder, og i undervisningen skal man derfor arbejde med både det dynamiske og det statiske funktionsbegreb og med at forbinde de to. Forskningen viser, at nogle elever kan udvikle en dynamisk og en statisk funktionsforståelse uden at kunne forbinde dem. (Kilde 7).
En model for læring, som bygger på disse to måder at forstå et begreb på, er beskrevet af matematikdidaktikeren Anna Sfard. (Kilde 2) Modellen indeholder tre stadier i dannelsen af matematiske begreber:
(1) Det første niveau kaldes internalisering (’indregørelse’). Her er begrebet endnu ikke helt klart for eleven. Det består af processer, der kan udføres og senere genkendes og benyttes sammen med allerede kendte begreber og processer. (2) Når man har udført disse processer igen og igen, og man bliver bedre og bedre til dem, vil man begynde at se på disse processer som et overordnet hele (måske i mindre dele), og det er ikke længere nødvendigt at gå i detaljer med, hvordan man udfører dem. Det er her, man begynder at se begrebet i sig selv, og dette kaldes kondenseringsfasen. (3) Sidste skridt i forståelsen af begrebet er, når eleven kan bruge det eller de dele, det består af, som en selvstændig ”ting” og ikke som en proces; dette kaldet reifikation (’tingsliggørelse’).
Under de første to stadier har eleven en operationel forståelse af begrebet, hvorimod det kræver en strukturel forståelse at nå op på det sidste stadium. Sagt med andre ord: ”Operationel forståelse er den eneste måde, hvorpå man kan komme i kontakt med de abstrakte begreber”. Dette er en pointe, der er meget væsentlig, i forbindelse med undervisningsplanlægning.
Morten Blomhøj har illustreret de forskellige faser i arbejdet med funktioner (Kilde 8). Her er mange af ovenstående pointer konkretiseret og uddybet.
Mogens Niss (Kilde 9) giver et overblik over den didaktiske viden om funktioner og udfordringerne. Centrale overblik kan også fås i (Kilde 10) og (Kilde 11).
emne: FUNKTIONER
UDGIVET: 2023
Forfatter
Lisbeth Fajstrup
Lektor, ph.d.
Institut for Matematiske Fag, AAU
Marit Hvalsøe Schou
Gymnasielærer, ph.d.
Odense Tekniske Gymnasium
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational studies in mathematics, 12(2), 151-169.
- Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational studies in mathematics, 22(1), 1-36.
- Steinbring, H. (2006). What makes a sign a mathematical sign? – An epistemological perspective on mathematical interaction. Educational studies in mathematics, 61, 133-162.
- Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational studies in mathematics, 61(1-2), 103-131.
- Steinbring, H. (1999). How do Mathematical Symbols acquire their Meaning? -The Methodology of the Epistemology-based Interaction Research. In Trabajo presentado en Annual Meeting of the GDM, Bern.
- Vinner, S., & Dreyfus, T. (1989). Images and definitions for the concept of function. Journal for research in mathematics education, 20(4), 356-366.
- Niss, M. A. (1999). Aspects of the nature and state of research in mathematics education. Educational Studies in Mathematics 40: 1-24, 1999.
- Blomhøj, M. (2016) ”Fagdidaktik i matematik”. Frydenlund.
- Niss, M. A. (2014). Functions. Learning and Teaching. Lerman, S. (eds.) Encyclopedia of Mathematics Education. Springer, Dordrecht. doi.org/10.1007/978-94-007-4978-8_96
- Carlson M., Oehrtman, M. (2005), Key Aspects of Knowing and Learning the Concept of Function. Mathematical Association of America, MAA Research Sampler 9.
- Dubinsky, E., Harel, G. (eds) (1992). The concept of function. Aspects of epistemology and pedagogy, vol 25, MAA notes, Mathematical Association of America, Washington DC.