Hvad er funktioner? Og hvorfor er funktionsbegrebet så vigtigt?

Igen bruges ordene ’sammenhæng’ og ’afhængighed’. Især ordet ’sammenhæng’ benyttes mange gange, og det er måske ikke helt klart, hvad ’en sammenhæng’ er. Det kan give vanskeligheder. I denne definition pointeres det også, at der kun kan være én y-værdi til hver x-værdi; en meget væsentlig egenskab for funktioner. Til gengæld indskrænker definitionen sig til at handle om tal. Senere må begrebet udvides.

Det er først i den mere abstrakte formulering som fx i Den Store Danske, at denne egenskab får sit eget ord: entydighed:

En definition af denne type, svarer til de definitioner, man også ser i gymnasiet. Selvom definitionen er mere abstrakt, genkender man sammenhæng og afhængighed i ordet ’regel’, og som nævnt bliver egenskaben at ”der kun kan høre én y-værdi til en x-værdi” nu beskrevet som entydighed. Endelig kan det være en pointe at bemærke for eleverne, at mængderne A og B ikke nødvendigvis er talmængder.

Den symbolske repræsentation af en funktion, $y = f(x)$, indkapsler den essentielle funktionsegenskab, nemlig at outputtet af funktionen - funktionsværdien - er entydigt bestemt af inputtet, x. Man kalder x for den uafhængige og y den afhængige variabel for at understrege denne egenskab. Definitionen af en funktion siger intet om, hvad der skaber sammenhængen mellem input og output - blot at den er entydig. Det kan imidlertid være vanskeligt for en elev at forstå en sådan definition, og det er helt naturligt. Entydighed er nemlig et begreb, som er krævende at forstå.

I definitionen oven for tales der om en forskrift eller regel. Her kan reglen bare være en sammenkædning af værdier af en uafhængig variabel x og en afhængig variabel y i en mængde af ordnede par (x, y), en (ofte uendelig) tabel, hvori alle x fra definitionsmængden A optræder. Funktionsegenskaben at ”der kun kan høre én y-værdi til en x-værdi” kræver alene, at der i mængden af ordnede par ikke findes forskellige par med samme førstekomponent, altså at hvert x fra A optræder præcis én gang.

På de videregående uddannelser har man ofte brug for en endnu bredere definition, som inkluderer flere typer af funktioner, end dem man har brug for i skolen, i erhvervsuddannelserne og på gymnasiet. Derfor arbejder man her med en definition af funktionsbegrebet, der er endnu mere abstrakt:

Hvis A og B er delmængder af de reelle tal, er $A×B$ punkter i planen, og definitionen siger altså, at en funktion er givet ved en graf. Betingelsen ”præcis” er netop entydigheden.

Det gør funktionsbegrebet til et meget generelt begreb. Definitionen siger for eksempel ikke noget om, hvad mængderne A og B er. I grundskolen og gymnasierne møder eleverne typisk en definition af en funktion som en variabelsammenhæng mellem en uafhængig og en afhængig variabel – der alene antager værdier fra talmængder – typisk $\mathbb{N}$, $\mathbb{Q}$ eller $\mathbb{R}$.

Hvorfor er funktioner så vigtige? Både i grundskolen og især i gymnasiet bruger man rigtig meget tid på at arbejde med funktioner, og det er der især to grunde til. Den ene er det matematikteoretiske aspekt: I de matematiktunge videregående uddannelser fylder funktionsbegrebet meget, og det er derfor vigtigt, at de kommende studerende har en solid forståelse af funktioner. Det er imidlertid kun en mindre del af en ungdomsårgang, som fortsætter på denne type uddannelse, så for mange elever er det den anden grund, som betyder mest: Funktioner er essentielle i praktiske anvendelser. Funktioner er fantastiske til at beskrive den hverdag vi lever i. Fra lineære funktioner, der beskriver vandforbrug i brusebadet efter gymnastiktimen over profitfunktioner i økonomi, til det helt spritmoderne: Et kunstigt neuralt netværk kan betragtes som en funktion, som har data som input og som output giver ja eller nej til, eksempelvis, om data er billedet af en kat. Det er yderst effektivt at tænke på netværket som en funktion, faktisk en funktion, der er sammensat af flere funktioner, også selvom vi ikke kender funktionsudtrykket.
Et andet eksempel er den ”bedste rette linje”, som eleverne ser i både grundskole og gymnasie. Her er input punkter i planen og output er en ret linje.

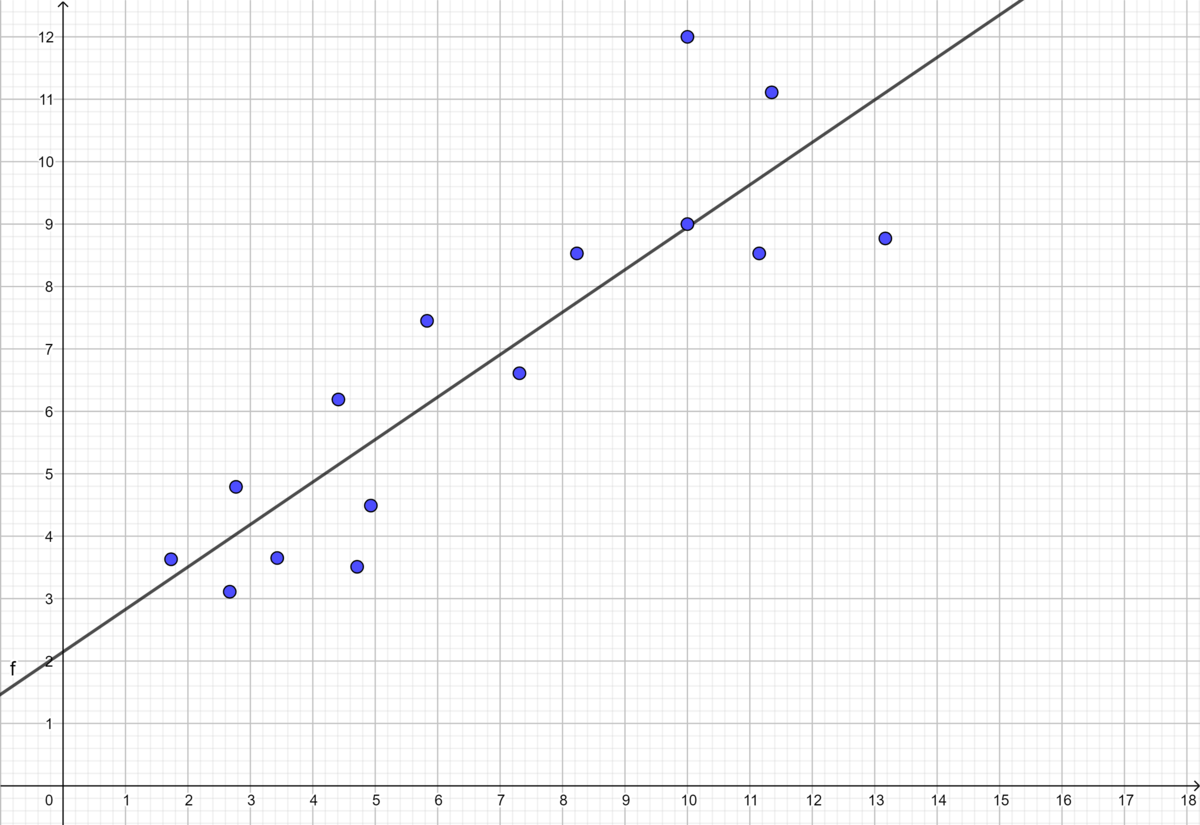
Funktioner er gode eksempler på, at en god definition og effektiv notation frigør tankerne. I eksemplet med bedste rette linje, er spørgsmål om, hvordan linjen afhænger af punkterne lettere at stille, når man indser, at der er en funktion i spil. Hvordan varierer linjen, når punkterne flyttes? Kan man tilføje punkter, som ikke ændrer på linjen? Og meget andet.

Funktioner er vigtige og bruges på alle niveauer både i modellering og internt matematisk. Funktionsbegrebet udvikler sig fra at være specielle sammenhænge mellem tal til meget mere generelle sammenhænge, som kan være mere mellem helt andre mængder end tal.