Hvordan kan man arbejde med funktionsbegrebet?
I matematikundervisningen arbejder man traditionelt med fire forskellige repræsentationer af funktioner:
- Sproglig beskrivelse
- Tabel
- Funktionsudtryk
- Graf
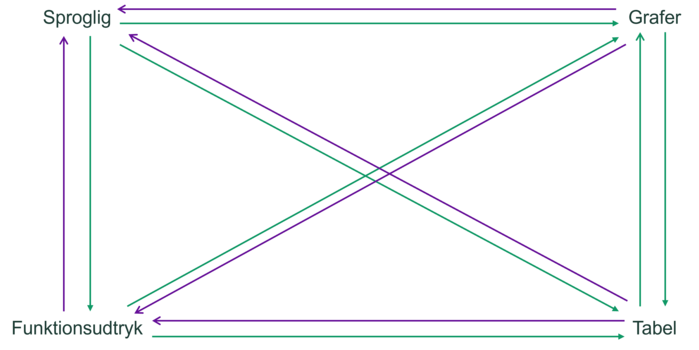
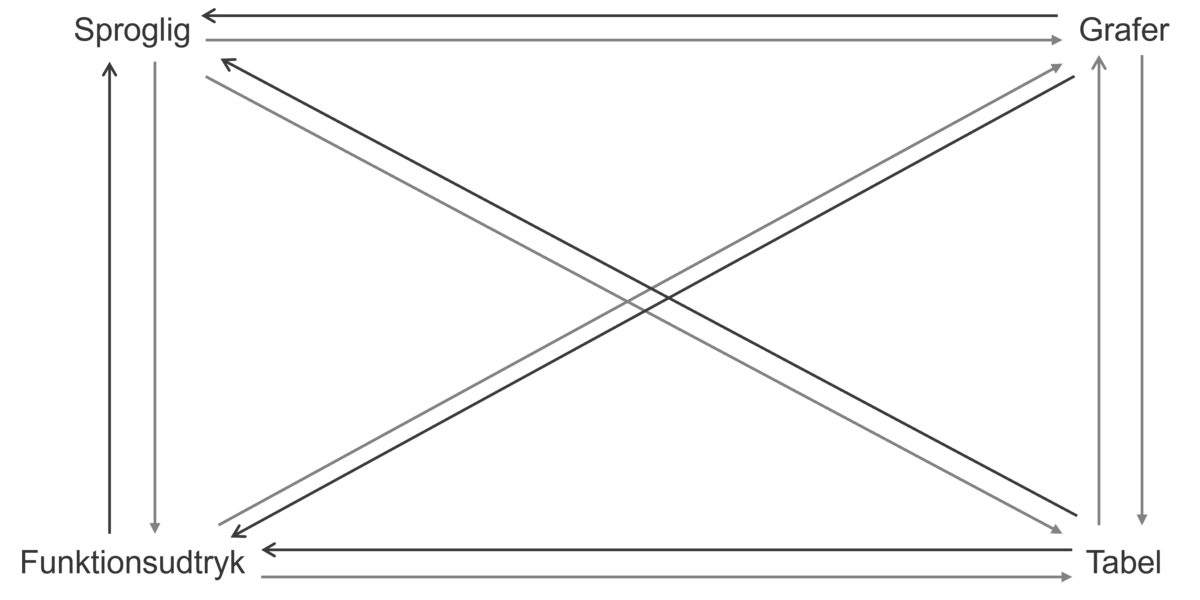
I dele af undervisningen vil man arbejde inden for den enkelte repræsentationsform, der har sine egne karakteristika og anvendelsesområder, men ofte vil man få brug for at kunne veksle imellem dem. Det er derfor vigtigt, at eleverne får mulighed for at bevæge sig langs pilene mellem de enkelte repræsentationsformer som vist på figur 1. Her symboliserer de grønne pile, de omformninger fra en repræsentationsform til en anden, der forekommer ofte i undervisningen, hvorimod de lilla pile forekommer mere sjældent. Nedenfor er nogle af pilene eksemplificeret.
Sproglig beskrivelse
Såvel modelleringsopgaver som problemløsningsopgaver begynder ofte med en sproglig beskrivelse af en variabelsammenhæng. Her må arbejdet starte med en undersøgelse af, om det overhovedet er en funktion, som beskrives? Hvad er den uafhængige og den afhængige variabel? For hvilke værdier er funktionen defineret?
Et eksempel er: ”Vi fylder vand i en spand i en konstant strøm. Der er to liter vand i spanden, når vi starter, og der er 4 liter vand, når der er gået 3 minutter. Vi vil beskrive sammenhængen mellem hvor lang tid, der er gået, og hvor meget vand, der er i spanden.” Formuleringen giver en direkte forbindelse til det, der modelleres, men kræver først en matematisering, altså en oversættelse til matematikkens mere præcise sprog, hvis man skal kunne konkludere noget ved brug af matematik. Når først denne matematisering er foretaget, kan mange elever komme frem til svaret, når de har en sproglig og symbolsk eller grafisk repræsentation. (Grøn pil).
En sproglig beskrivelse som ”Den lineære funktion, hvis graf går gennem (0,2) og (5,4)” er mere abstrakt, men er stadig sproglig og kræver bearbejdning, hvis der skal konkluderes noget. Dette kan gøres vha. et funktionsudtryk eller en graf. En anden sproglig beskrivelse kunne være ”Den lineære funktion, som har hældning $\frac{2}{5}$ og rammer y-aksen i (0,2)”. I gymnasiet vil man møde sproglige beskrivelser som ”Den funktion f, hvis afledte er konstant $\frac{2}{5}$, og som opfylder, at $f(5)=4$”. (Grøn pil).
Eksemplerne viser, hvordan man kan bevæge sig fra den sproglige repræsentation til andre repræsentationsformer. Et eksempel på den modsatte problemstilling, altså hvor eleverne skal bevæge sig mod en sproglig beskrivelse er følgende, hvor et funktionsudtryk skal fortolkes i en konkret kontekst. (Lilla pil).
- Fortæl en kort historie, der handler om prisen på en isvaffel, som kan beskrives ved den lineære funktion $f(x)=18+8\cdot x$.
- Forklar også betydningen af tallene 18 and 8 i formlen.

Et andet eksempel, hvor man bevæger sig mod den sproglige beskrivelse, ses her.
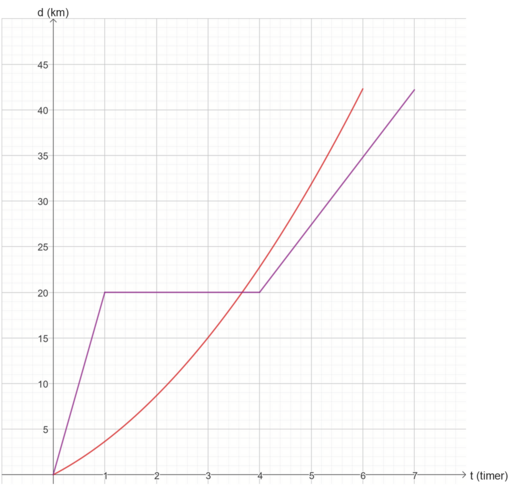
De to venner Morten og Malene løber et maraton. Graferne viser, hvor langt de er nået som funktion af tiden. Mortens løb er beskrevet ved den lilla graf og Malenes ved den røde. Lav en historie om de to venners maratonløb. I historien skal der (mindst) indgå oplysninger om:
- Hvor langt løber Morten den første time? Og med hvilken fart?
- Hvad laver han efter der er gået en time? Og hvor længe gør han det?!
- Hvem kommer først i mål?
- Hvad er Malenes gennemsnitsfart?
- Løber Morten hurtigere eller langsommere de sidste 3 timer i forhold til den første time?
- Er Malenes fart voksende eller aftagende? (Man kan også spørge, om hun løber hurtigere og hurtigere, eller om hun løber langsommere og langsommere.)
- Hvem af de to kommer først i mål?
Tabeller
Har man et funktionsudtryk eller en graf, kan man nemt lave en tabel. Den anden vej er straks værre:
Lige som ved den sproglige repræsentation vil mange modelleringsopgaver starte med en tabel. Her finder man de data, som skal modelleres. I nogle situationer, er det eleverne selv, der har fremskaffet data i tabellen. Modelleringen kan gå ud på at finde en funktion, som passer til data. Altså at nå fra tabel til funktionsudtryk eller graf. I modelleringen må man overveje, hvilke typer funktioner, man vil bruge – ofte ud fra viden om det, der modelleres.
Tabellens data kan nemt indtegnes i et koordinatsystem. Men for at kunne lave en sammenhængende graf, er der brug for yderligere oplysninger: er funktionen overhovedet kontinuert, eller ER der ikke andet end de indtegnede punkter? Hvilken type funktion er der tale om?

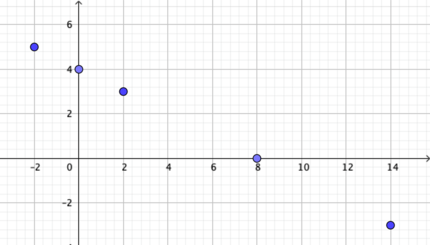
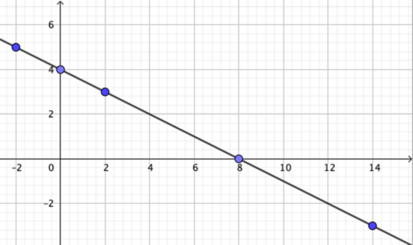
Ovenstående tabel beskriver en funktion, som er defineret i -2, 0, 2, 8 og 14 og sammen med funktionsværdierne giver punkterne (-2 , 5), (0 , 4), (2 , 3), (8 , 0) og (14 , -3). I koordinatsystemet på figur 2 er punkterne indtegnet i et koordinatsystem. Først når man tilføjer, at det for eksempel er en lineær funktion fra de reelle tal til de reelle tal, kan man udlede et funktionsudtryk eller tegne en (sammenhængende) graf for denne funktion ud fra oplysningerne i tabellen som vist på figur 3.
Der findes imidlertid uendelig mange funktioner, defineret på de reelle tal, med funktionsværdier som vist i tabellen. Det indser man måske bedst ved at tegne grafer, som passerer igennem alle punkter som vist på nedenstående figur 4.
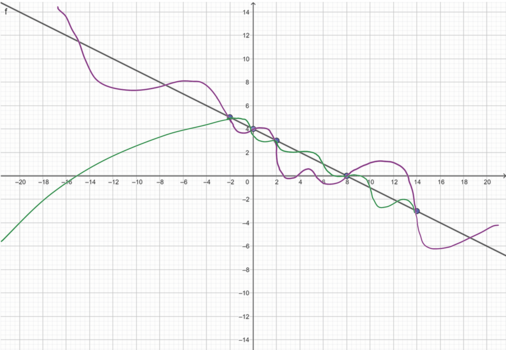
En tabel for en reel funktion er altså ufuldstændig information, hvis ikke den enten tabellægger $(x, f(x))$ for alle $x$ i definitionsmængden eller har yderligere information – såsom at funktionen er lineær eller et 5.gradspolynomium.
Den abstrakte definition af en funktion $f: A \rightarrow B$ siger, at f er en mængde af par $(a,b)$ med $a\in A$ og $b\in B$ sådan at ethvert $a\in A$ er i præcis ét par. Funktionen er således defineret som en tabel. Men, hvis $A$ er en uendelig mængde, er det en uendelig stor tabel!
Når data fra tabellen ikke ligger på en ret linje, kan man alligevel lave en lineær model, nemlig ved at bestemme den bedste rette linje. For at få en fornemmelse af linjens beliggenhed, kan man tegne punkterne ind på papir og benytte en lineal, der flyttes rundt, til man skønner at have den ´bedste´ rette linje. Denne linje kan sammenlignes med det resultat, man får, ved at anvende lineær regression på data. Det kan lyde gammeldags at bruge lineal! Men der er faktisk en pointe i at lade eleverne selv forsøge sig med at finde den bedste rette linje, og opdage, at det ikke er helt nemt. Samtidig er det en god anledning til få talt om, hvad ordet ”bedst” betyder.
En problemstilling som nedenstående kan give eleverne mulighed for at se, forskellen på at inddrage ALLE datapunkter som ved lineær regression, eller kun et udvalgt par af punkter til at finde den lineære funktion. (Grøn pil).

Jonathan og hans familie skal på ferie og kører gennem Tyskland. I bilen er det muligt at følge med i, hvor meget benzin, der er tilbage i tanken. Tabellen viser samhørende værdier af den afstand familien har kørt, x, og mængden af benzin, y, i tanken.

- Indtegn de 5 punkter i et koordinatsystem.
- Opstil en forskrift for den lineære funktion, der går gennem de to grønne punkter og tegn grafen.
- Opstil en forskrift for den lineære funktion, der går gennem de to blå punkter og tegn grafen.
- Tegn ‘den bedste rette linje’ gennem alle 5 punkter og benyt dit IT-redskab til at beregne forskriften for den lineære model, der bedst beskriver data i tabellen.
- Kommentér resultatet. Hvad har du vist?
Funktionsudtryk eller forskrift
Et funktionsudtryk er en algebraisk beskrivelse af sammenhængen mellem input – den uafhængige variabel – og output. I grundskolen er der fokus på lineære funktioner, hvor $f(x)=a \cdot x +b$, men der arbejdes også med andre typer af funktioner herunder stykkevis lineære funktioner. I gymnasiet fortsætter arbejdet med funktioner, og der introduceres nye typer: potensfunktioner, polynomier, eksponentialfunktioner osv.
Ikke alle funktioner har et simpelt funktionsudtryk, fx normalfordelingens fordelingsfunktion, selvom frekvensfunktionen har et algebraisk/analytisk udtryk.
Grafer
Grafer giver en visuelt appellerende fremstilling, og mange egenskaber ved funktionen springer i øjnene: største- og mindsteværdi, spring i funktionsværdier (diskontinuitet), som vel at mærke ligger i det område, man har valgt at tegne grafen for – det kan give fejlslutninger, hvis man forsøger at konkludere for inputværdier, der ikke er med. Man kan ikke ”regne” direkte ud fra en graf, men mange egenskaber ved funktioner kan illustreres med grafer. Arbejdet med grafer uddybes i afsnittet Meget mere om grafer.
Vekslen mellem repræsentationsformerne
Mestring af funktionsbegrebet kræver, at eleven kan skifte mellem disse repræsentationer og vælge den bedste i givne situationer (Kilde 1). Eksempelvis når resultatet af en modellering skal præsenteres. Følgende eksempel viser, hvordan eleverne kan få øjnene op for styrker og svagheder ved de fire repræsentationsformer.
Find en funktion i klasselokalet/på skolen/derhjemme, som er givet ved en af de fire repræsentationer.
- Angiv din funktion i så mange forskellige repræsentationer, som du kan.
- Hvilke fordele/ulemper er der ved hver repræsentationsform?
- Hvilken af pilene viser den sværeste omformning?
Og den letteste? - Hvornår bruger vi typisk de forskellige repræsentationsformer? Og hvorfor?
Til lærerteamet:
- Diskuter hvordan I arbejder med de forskellige repræsentationsformer. Er der nogle, der bliver brugt mere end andre? Er der nogle, der næsten bliver glemt?
- Og hvordan støtter I eleverne i at veksle mellem de forskellige repræsentationsformer?
- Er I enige i, hvilke pile på figur 1, der er grønne, og hvilke der er lilla?
- Find og del egne erfaringer med forskellige aktiviteter, der kan støtte eleverne i at veksle mellem repræsentationsformerne.
- Evaluer jeres egen praksis og giv eksempler på de grønne pile og de lilla pile.
Meget mere om grafer
Grafer er en meget visuel måde at repræsentere funktioner på, og derfor er de også velegnede til at synliggøre vigtige pointer ved funktionsbegrebet. Imidlertid kan man nemt komme til at overse nogle af de matematiske forhold som gælder for grafer, og som ofte er skjulte, (Kilde 2). Det kan for eksempel være forståelsen af, at et punkt på en graf er et talpar, der angiver forbindelsen mellem to størrelser, eller det kan være det konstante forhold, der er imellem inddelingerne på akserne. Også den måde vi forbinder hældningen af en graf med, om funktionen er voksende, aftagende eller konstant er ofte skjult for eleverne. For nogle elever er denne sammenhæng helt uden mening, på samme måde som en elev kan fortælle at: ”forskriften for en lineær funktion er $f(x)=a \cdot x + b$, hvor a er hældningen og b er skæring med y-aksen”, men uden eleven har nogen som helst forståelse for, hvorfor dette er opfyldt!
Her kommer derfor et eksempel (fra kilde 2), som viser hvordan man kan lade elever undersøge og opdage, hvordan man kan bruge grafer til at analysere sammenhængen mellem to variable.
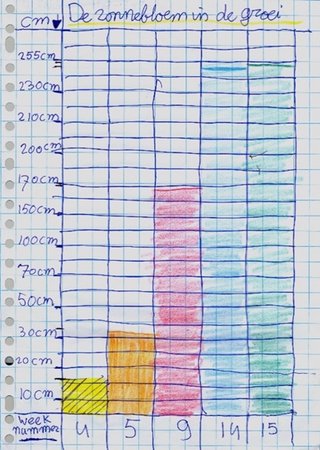
Allerede i 3.-4. klasse kan elever måle sammenhørende værdier fx tiden, der går og højden af en solsikke. Her opfattes højden som en egenskab ved solsikken, og eleverne måler højden hver dag i en periode. Men hvordan kan man vise, hvordan blomsten er vokset? Nogle elever vil måske tage billeder af solsikken sammen med en tommestok, andre vil tegne blomsterne med den målte højde indtil de bliver for store. Måske får de herefter den idé, at det er nok at vise højden - uden blomst - og mere skematisk som på figur 5. Gennem fælles klassediskussion kan man komme frem til en første måde at vise, hvordan blomsten er vokset på. Det kan være en ”søjlegraf” hvor eleverne tegner solsikkens højde ud for den dag, de har målt denne højde.
På mellemtrinnet, dvs. 4.-6. klasse, er det vigtigt at eleverne opdager pointer som:
- At de har glemt de dage eller uger, hvor der ikke er målt – weekenderne. Det giver pludselige og store ændringer.
- At solsikker vokser, selvom man ikke måler på dem, så der må være værdier på ”tidsaksen”, der ikke er med.
- At det giver et bedre billede, når ”højde-aksen” også er proportional.
Det næste skridt er at forbedre ”søjlegrafen” ud fra de opdagelser, eleverne har gjort: behovet for proportionalitet på begge akser, og at der er højder (funktionsværdier) imellem dem, der er målt. Måske har eleverne brug for at tegne søjler igen, men denne gang med proportionale akser. For også at få alle de højder, man IKKE har målt, med, kan søjlernes øverste endepunkter forbindes.

For at kunne ræsonnere om sammenhængen mellem tid og højde, skal eleverne gå fra at opfatte målene som en fast egenskab ved solsikken, til at højderne er et udvalg af værdier for en variabel, der kan variere over et bestemt interval. Tiden kan variere mellem f.eks. 0 dage og 15 dage og blomstens højde kan variere mellem 5 cm og 250 cm. Derfor er næste skridt, at søjlerne ikke længere er nødvendige. Man har bare brug for at vide, hvor høj blomsten er til et bestemt tidspunkt. I stedet for hele søjlen har vi kun brug for endepunktet, og endepunkterne kan forbindes med linjestykker for at få de manglende højder med. Det fører til en graf som vist på figur 6, og den skal gerne føre til en ny diskussion af, at de knæk, der opstår, nok ikke er realistiske – så man må glatte grafen ud.
Eleverne er nu nået frem til en sammenhængende graf, og den er på den ene side statisk men viser samtidig, at data ændrer sig dynamisk.
Til lærerteamet:
- Hvilke andre spørgsmål og konventioner for grafer kan eleverne udforske i denne aktivitet?
- Hvilken indsigt i funktionsbegrebet kan de opnå gennem aktiviteten?
- Hvis eleverne har målt på mange solsikker, kan I overveje, om de er klar til at se på spørgsmål om, hvordan solsikker generelt vokser. I gennemsnit for eksempel.
Ved at arbejde med at tegne og undersøge grafer, der beskriver sammenhænge givet ved en konkret kontekst, understøtter man primært opfattelsen af en funktion som en proces. Denne tænkning er vigtig og kræver tid og mange eksempler. Senere kan man støtte eleverne i at forstå funktioner som objekter, og her kan aktiviteter med grafer være en god måde at arbejde på. Man kan grafisk lægge funktioner sammen, trække dem fra hinanden, gange dem med en konstant, osv. som i følgende aktivitet, der benytter en genkendelig kontekst. Aktiviteten kan anvendes i 8.-9. klasse.
Ella og Klara tager bad efter gymnastik. Bruserne i omklædningsrummet giver ikke lige meget vand. Figuren viser, hvor meget vand hver af pigerne bruger i løbet af 5 minutter
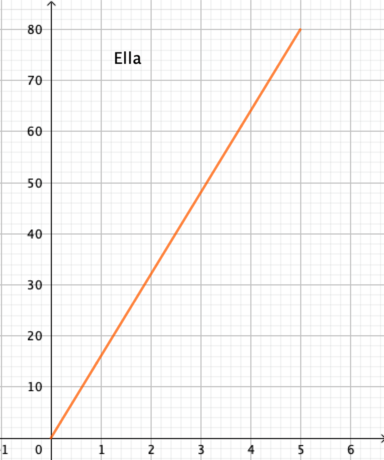
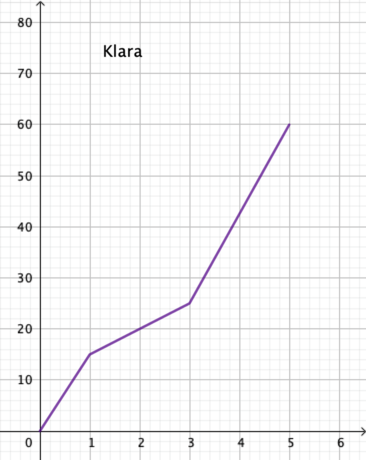
Spørgsmål som nedenstående kan hjælpe eleverne til at tegne en graf for det samlede vandforbrug som summen af de to pigers individuelle forbrug.
- Hvor meget vand har Ella brugt efter 1 minut?
- Hvor meget har Klara brugt?
- Hvad har de brugt tilsammen?
- Hvor meget vand har pigerne brugt tilsammen efter 5 min.?
- Hvor lang tid går der, før de tilsammen har brugt 75 l?
For at lære om sumfunktioner og skabe mening i den tilhørende algebraiske notation, arbejder eleverne med en helt konkret kontekst, et brusebad efter en gymnastiktime. Den mængde vand, pigerne Ella og Klara hver især bruger, er beskrevet som en tekst og skal afsættes som grafer i et koordinatsystem, og ud fra graferne kan eleverne uddrage forskellige oplysninger om situationen, og de kan tegne grafen for pigernes samlede vandforbrug. Sumfunktionen, der er den egentlige genstand for aktiviteten, har også en symbolsk repræsentation, som eleverne kan komme frem til ved hjælp af graferne evt. i samspil med den sproglige beskrivelse. Gennem arbejdet med graferne kan funktionen undersøges og forstås. Det samlede funktionsbegreb bygger på mange konkrete eksempler som f.eks. de sumfunktioner, der arbejdes med her, og det er gennem sådanne eksempler, at eleverne opnår viden om begrebet. Specielt er det gennem arbejdet med funktionens symbolske repræsentation, at eleverne kan erkende strukturelle og generelle egenskaber ved funktionsbegrebet.
Tilsvarende problemstillinger kan støtte eleverne i at undersøge, hvad der sker, når man trækker to funktioner fra hinanden, ganger dem med hinanden eller ganger med et tal. Altså egenskaber ved funktionerne
$h=f-g$ altså $h(x)=f(x)-g(x)$
$p=f \cdot g$ altså $p(x)=f(x) \cdot g(x)$
$q=k \cdot f$, hvor k er et reelt tal altså $q(x)=k \cdot f(x)$
ud fra deres grafer. I ovenstående kontekst kan man fx tale om hvor meget badet koster, ved at gange vandforbruget med prisen på en liter vand.
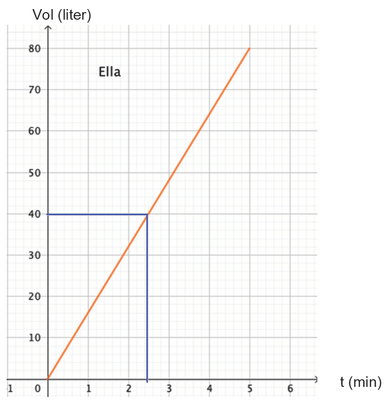
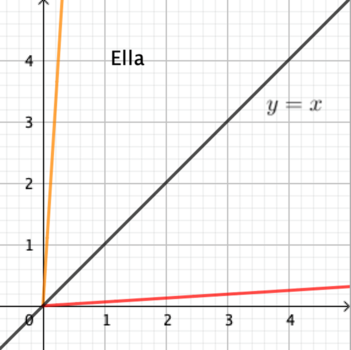
Man kan også se på omvendte (inverse) funktioner. Vi kigger på grafen, Figur 7a, der viser Ellas vandforbrug. Den omvendte funktion beskriver hvor lang tid, der er gået i badet som funktion af, hvor meget vand, Ella har brugt. Det kan elever aflæse på vandforbrugsgrafen ved at se, hvordan en værdi på y-aksen svarer til en værdi på x-aksen. Det svarer til at gå vandret og så lodret langs de blå linjer, hvor aflæsning af vand som funktion af tid går lodret og så vandret. Man kan f.eks. spørge: ”Hvor lang tid går der, før Ella har brugt 40 liter vand?” Eller mere generelt: Den omvendte funktion er ”undo”. De to funktioner er hinandens omvendte. Grafen for den omvendte funktion er Figur 7b.
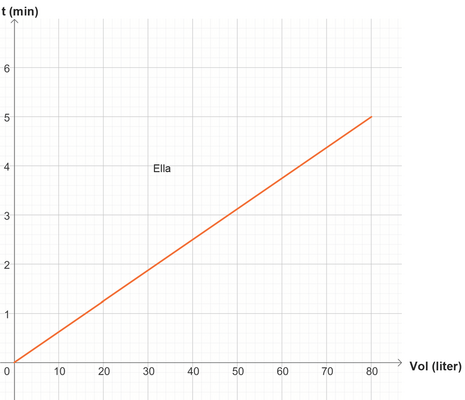
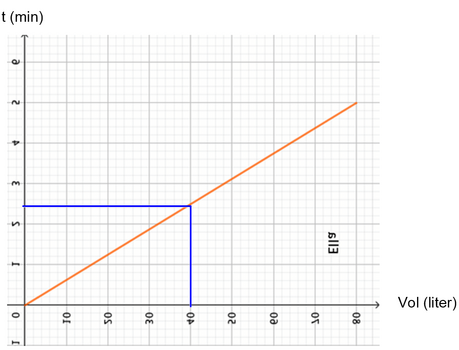
Man bemærker, se Figur 8a, at grafen for den inverse funktion netop svarer til at spejle grafen for funktionen i linjen y = x, og hvis man arbejder med tabeller, svarer det til at bytte om på tabellens to rækker. I anvendelser som her, giver det ikke mening at tegne begge grafer i samme koordinatsystem som i 8b. Der er forskellige enheder. Det er således vigtigt, at eleverne ikke kun har denne geometriske opskrift, men også forstår, at den omvendte funktion ”går den anden vej” – fra vandforbrug til tid. Og at ikke alle funktioner har en omvendt funktion. (Kilde 3 og 4).
I gymnasiet kan ovenstående egenskaber tages op igen ud fra grafer, og undersøgelserne kan udvides til også at omfatte funktioner givet ved deres forskrift. Dette er et vigtigt forarbejde i forhold til introduktion af differentialkvotienten (og den afledte funktion), som hældningen af funktionens graf. Når man senere vil bevise sætninger om differentiabilitet af sum, differens osv. af funktioner, er det af stor betydning, at eleverne kan tillægge disse mening, så det ikke blot bliver ”symbolgymnastik”.
Til fagteamet:
- Hvilke andre spørgsmål med udgangspunkt i grafer kan eleverne udforske i denne aktivitet?
- Hvilke indsigter i funktionsbegrebet kan de opnå gennem aktiviteten?
- Der lægges oftest op til at arbejde med funktioner som en proces. Men det er også vigtigt at eleverne opnår forståelse for funktioner som et objekt. Hvordan arbejder I med objektforståelsen af funktioner? Giv gerne eksempler.
Grafen for en funktion er et billede af hele funktionen på én gang, et helhedsindtryk om man vil, men kun på en begrænset definitionsmængde. Eleverne kan arbejde med grafer uden at kende hverken funktionsudtryk eller tabeller. Det giver mulighed for, at man allerede i grundskolen kan veksle mellem proces-synspunktet, hvor en funktion evalueres i en værdi ad gangen, og objekt-synspunktet.
Her ses eksempler på spørgsmål, man kan stille om grafer såvel i udskolingen som på gymnasiet.
Her ses grafen for en funktion f.
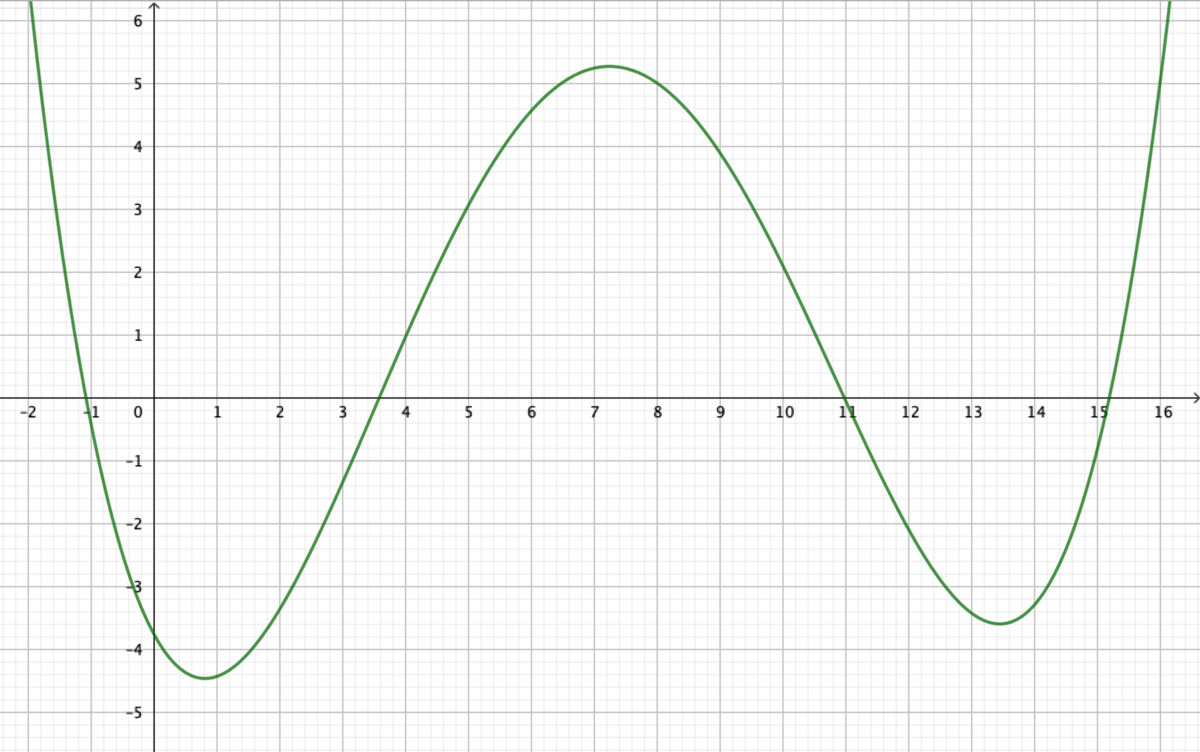
- Hvordan kan man aflæse $f(4)$?
- Hvor ligger punktet $(8,f(8))$?
- Kan man aflæse løsning(er) til ligningen $f(x)=3$?
- Hvor mange løsninger er der til ligningen $f(x)=2$? $f(x)=6$??
- Hvordan ser grafen ud for en funktion, hvor ligningen $f(x)=k$ altid har præcis én løsning, uanset hvad $k$ er?
- Er der tal $x$, hvor $f(x)=x$? (Her må læreren evt. illustrere, hvordan man kan bruge skæring af grafen for $f$ med linjen $y=x$ til at svare på spørgsmålet.)
En funktion beskriver en sammenhæng mellem variable. I stedet for at fokusere på funktionsværdier én ad gangen, som man gør i et proces-perspektiv, kan man undersøge, hvordan funktionsværdierne varierer, når man varierer input. På denne måde kombineres de to perspektiver (proces- og objektforståelsen), idet aflæsning af funktionsværdier kan være med til at afgøre, om funktionen vokser eller aftager samt oplevelsen af, at man kan se på grafens forløb, uden det er nødvendigt at se på funktionsværdierne.
Her ses grafen for en funktion f.

[Indsæt selv grafen for en passende funktion. Sværhedsgraden kan tilpasses eleverne ved valg af f.]
- Hvad kan I sige om, hvordan funktionen varierer – brug for eksempel ord som, at den stiger (vokser), falder (aftager), er uændret (konstant), er stejl, osv.
- Hvor stor kan f(x) maksimalt blive? Hvordan ser man det på grafen?
- Tegn grafer, hvor der ikke er grænser for, hvor stor f(x) kan blive.
Og for gymnasiet:
- Prøv at tegne en graf for en funktion g, der beskriver variationen af f:
- g(x) skal være positiv, når f vokser
- g(x) er negativ, når f falder/aftager.
- Jo mere (stejlere) f vokser, jo større skal g(x) være.
Til lærerteamet:
- Hvad kan eleverne få ud af at arbejde med en kontekstfri situation som i denne opgave?
For nogle funktioner findes der kun grafen. Det er ikke muligt at finde nogle af de andre repræsentationsformer på fornuftig vis. Et eksempel på sådan en graf med tilhørende opgave er:
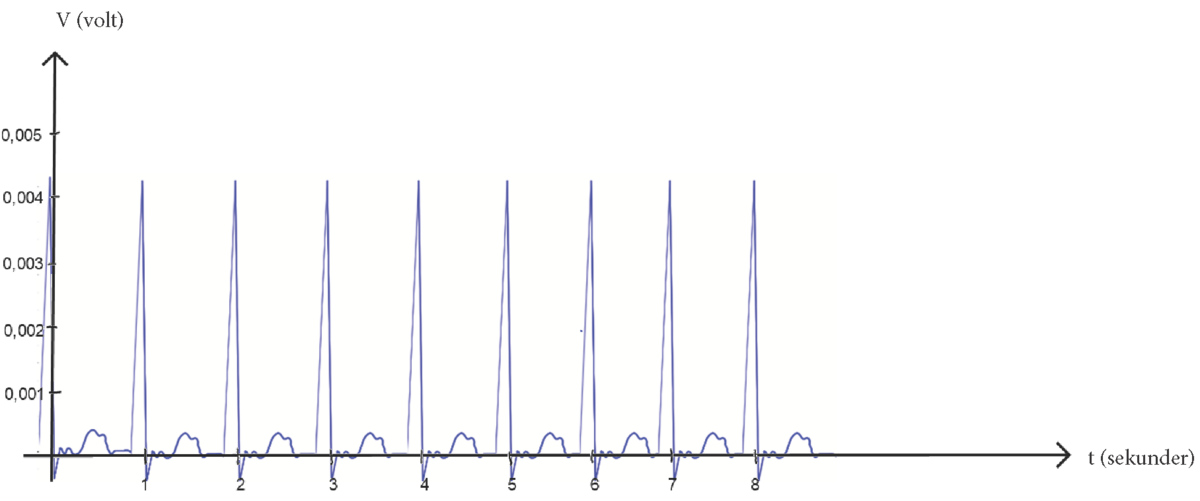
Et relevant spørgsmål kunne være:
Et EKG, ElektroKardioGram, viser de elektriske impulser, der sendes gennem hjertet og sørger for, at hjertet slår regelmæssigt. Grafen viser den elektriske aktivitet i Volt som funktion af tiden målt i sekunder. Hver top svarer til et hjerteslag.
- Hvad er hjerterytmen (hjerteslag i minuttet) for denne patient?
emne: FUNKTIONER
UDGIVET: 2023
Forfatter
Lisbeth Fajstrup
Lektor, ph.d.
Institut for Matematiske Fag, AAU
Marit Hvalsøe Schou
Gymnasielærer, ph.d.
Odense Tekniske Gymnasium
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational studies in mathematics, 61(1-2), 103-131.
- Gravemeijer, K. (2020) Emergent Modeling: an RME Design Heuristic Elaborated in a Series of Examples.
- Wilson, F.C., Adamson, S., Cox, T., and O’Bryan, A. (March 2011). Inverse functions: What our teachers didn’t tell us. Mathematics Teacher. 104, pp. 500-507.
- Stevens, I.E., Ko, I., Paoletti, T., Boileau, N., Herbst, P. Introducing inverse functions to high school students: Relating Convention and reasoning. Algebra, Algebraic Thinking and Number Concepts. Proceedings of the 42nd Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education.