Idéer til undervisningsaktiviteter med funktioner på forskellige klassetrin
Begrebet funktioner omfatter rigtig mange ting, og der findes rigtig mange forskellige funktionstyper. Nogle funktioner har ikke tal som input og output, nogle funktioner har ingen forskrift osv. Her vil vi præsentere nogle funktioner, der er helt anderledes end dem, vi er vant til at arbejde med, og vi vil beskrive aktiviteter, der fokuserer på andre aspekter af arbejdet med funktioner end man sædvanligvis beskæftiger sig med i undervisningen.
“Anderledes funktioner”
Nedenstående eksempler viser funktioner, hvor input- og/eller outputmængderne ikke er tal, som vi er vant til.
QR-koder (Quick Response)

Til en QR-kode hører oftest en web-adresse, men det kan også være for eksempel kreditkortinformation, information til Mobile Pay eller togbilletter. Mobiltelefonens QR-læsnings-app kender funktionen fra QR-kode til web-adresse eller andet.
Stregkoder
Til en stregkode på en vare i et bestemt supermarked hører en pris. Man kan her tale med eleverne om, hvordan denne funktion også afhænger af dato og muligvis også af tidspunkt på dagen, samt at evt. mængderabat ikke ændrer på, at det en funktion – input til den samlede pris er jo flere stregkoder eller flere gange den samme stregkode og mængderabat kan udtrykkes som f(3xStregkode) er mindre end 3xf(Stregkode). Kasseapparatet har denne funktion indbygget. (Det er faktisk en sammensat funktion: Der er en stribe tal på sådan en stregkode. De indeholder samme information som stregerne. Det udnytter kassemedarbejderen, som indtaster tallene, hvis stregkoden er ødelagt. Scanneren på kasseapparatet kan læse stregerne, kasseapparatet har en funktion fra streger til tal, og der er så endnu en funktion fra tal til pris.) https://www.gs1.dk/gs1-standarder/maerkning-stregkoder-og-rfid/ean-og-upc/
Spørger man gymnasieelever, om prisen på et indkøb i det lokale supermarked er en funktion af stregkoderne på varerne, siger de allerfleste elever klart nej. Man kan jo ikke udregne prisen fra stregkoderne. De tænker ikke på, at præcis det samme indkøb netop ikke må give forskellig samlet pris.
CPR-nummeret
Funktionen, der har danske statsborgere som inputmængde og som output giver CPR-nummer.
Kunstige Neurale Netværk
Et kunstigt neuralt netværk kan, når det er trænet, behandle input i form af eksempelvis et billede og give som output, om der er en kat på billedet. Det er en funktion. Billede ind, ja/nej ud.
Når netværket trænes, er det funktionen, der skal justeres ind. Her er input træningsdata og output er funktionen, der derefter bruges til at finde katte. Se mere om neurale netværk på https://aalborg-intelligence.ai/
For nogle funktioner er input- og/eller output ikke blot ét men flere tal.
Den bedste rette linje i et nyt perspektiv
Et andet eksempel ligger gemt i ”den bedste rette linje”. Når man benytter regression enten i grundskolen eller i gymnasiet, kan man diskutere denne problemstilling:
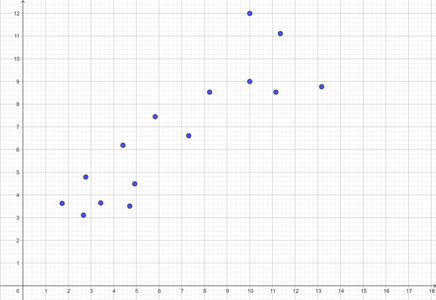
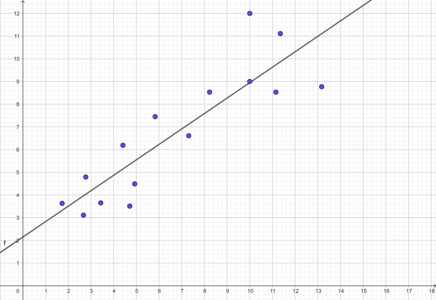
Punkterne i planen på figur 1 giver anledning til en lineær funktion. Den er bestemt ved de to tal, a og b i forskriften $f(x)=a \cdot x + b$ , som her er a = 0,68, b = 2,15 vist på figur 2.
Vi har altså en funktion, der med disse 15 punkter som input: (1.73,3.63), (3.43,3.65), (4.41,6.19), (7.31,6.61), (5.83,7.45), (10,9), (8.23,8.53), (11.35, 11,11), (13.17, 8.77), (2.77, 4.79), (4.93, 4.49), (4.71, 3.51), (2.67, 3.11), (11.15, 8.53), (10,12), giver et talpar (0.68, 2.15) af reelle tal som output.
Eksemplet kan give anledning til spørgsmål som:
- Hvad er inputmængden for sådan en funktion? Der er ikke altid 15 punkter, det må nok være noget med mængden af endelige mængder af talpar.
- Kan man nøjes med ét punkt?
- Hvad nu, hvis man har to punkter (x, y1) og (x, y2) med samme førstekoordinat?
- Er det ok med en ret linje parallelt med y-aksen? I så fald er det ikke hældningen og skæring med y-aksen, der karakteriserer linjen, så måske vil vi begrænse de mulige input eller ændre de mulige output.
- Hvordan varierer linjen, når punkterne flyttes? Kan man tilføje punkter, som ikke ændrer på linjen?
Funktioner er gode eksempler på, at en god definition og effektiv notation frigør tankerne. I eksemplet her med bedste rette linje, er spørgsmålet om, hvordan linjen afhænger af punkterne lettere at stille, når man indser, at der er en funktion i spil.
BMI
Funktionen, der til en persons højde og vægt giver BMI, er givet ved forskriften $BMI(h,v)=\frac{v}{h^2}$ . Med højden h målt i m og vægten v i kg er enheden kg/m2. Her har man en funktion af to variable. Se mere om BMI i temaet
Funktioner uden en forskrift
Der findes rigtig mange funktioner, som man ikke har en forskrift på. Nogle er givet ved en sproglig beskrivelse, andre ved en graf eller ved en tabel. Et hverdagseksempel herpå er prisen på en vare som funktion af stregkoden.
Trekanttal
Trekanttal har en fin geometrisk beskrivelse, som kan ses på figuren
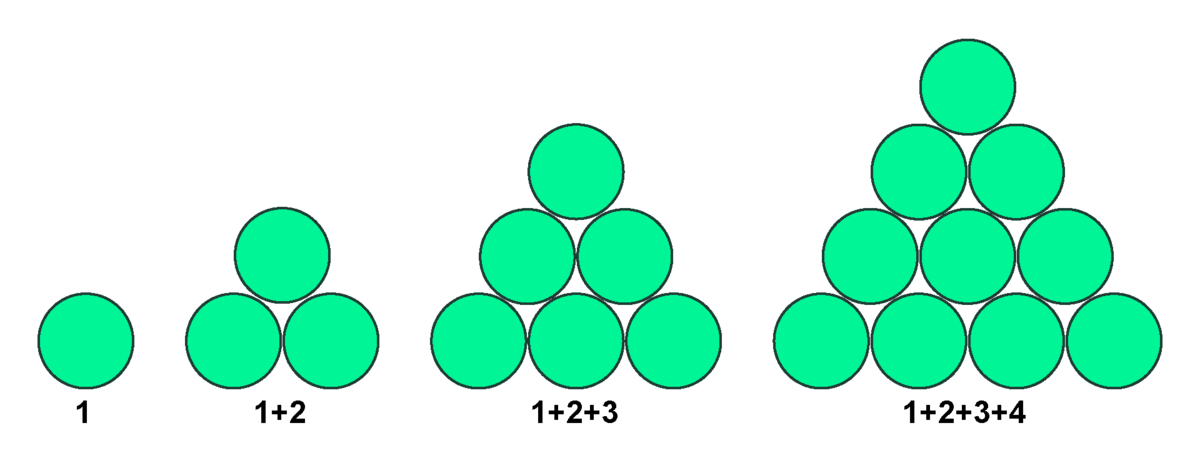
Trekanttallene er tallene 1, 1+2, 1+2+3, 1+2+3+4, … og beskriver en funktion fra naturlige tal til naturlige tal.
Funktionen kan også beskrives rekursivt
$T(n)=T(n-1)+n$, med $T(0)=0$
Eller med summationstegn $T(n)=\sum_{k=1}^nk$ og man kan faktisk vise, at $T(n)=\frac{n(n+1)}{2}$, så funktionen har et funktionsudtryk.
Den rekursive beskrivelse fremkommer fra den geometriske beskrivelse, og den giver en anden indsigt end funktionsudtrykket. Til gengæld giver funktionsudtrykket mulighed for at udregne eksempelvis T(100) direkte. Den rekursive beskrivelse kræver udregning af T(99), som kræver udregning af T(98) osv.
Fakultetsfunktionen
For et naturligt tal n er $n!=n \cdot (n-1) \cdot (n-2) \dots 1$.
Det giver en funktion fra de naturlige tal til de naturlige tal, F(n). Den kaldes fakultetsfunktion, og den kan defineres rekursivt:
$F(n)=F(n-1) \cdot n$ med $F(0)=1$.
Der findes ikke et kort og enkelt funktionsudtryk, der direkte giver F(n) ved indsættelse af n, som det er tilfældet for T(n). Udregning af n! kræver multiplikation af n tal. Fakultetsfunktionen bruges i forskellige matematiske områder og i mange anvendelser. Det er derfor praktisk, at den har fået sit eget symbol i form af udråbstegnet, så man helt kort kan skrive $F(n) = n!$
Den rekursive ligning beskriver fakultetsfunktionen fuldstændigt for de naturlige tal.
Der findes en funktion $\Gamma$ , som er defineret for alle positive reelle tal og opfylder $\Gamma(x+1)=(x+1)\Gamma(x)$ og $\Gamma(1)=1$ . Og altså for de naturlige tal: $n!=\Gamma(n+1)$
De danske matematikere Harald Bohr og Johannes Mollerup viste i 1922, at Gammafunktionen er den eneste funktion, der opfylder de to betingelser og en tredje, nemlig at $\ln \circ \Gamma$ er konveks (grafen er opad hul). Gammafunktionen kan udtrykkes som et ubestemt integrale
$\Gamma(x)=\int_0^\infty t^{x-1}e^{- t}dt$
Nu har vi altså fundet et udtryk for n! som et integrale. Det er stadig ikke et simpelt udtryk. Gamma er simpelthen et navn for dette integrale.
Decimaler i $\pi$
Funktionen givet sprogligt ved, at f(n) er den n’te decimal i $\pi$ , er en funktion fra de naturlige tal til de naturlige tal. Den har ikke noget kendt funktionsudtryk med elementære funktioner, men det er alligevel en funktion.
Transcendent ligning
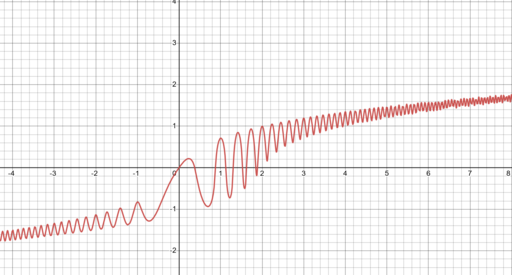
Til slut ser vi på et eksempel på en variabelsammenhæng, en såkaldt transcendent ligning $y^3+2^y=\cos(2\pi x^2)+x$ mellem de variable x og y. Man kan vise, at denne ligning har præcis en løsning y for hvert x. Det giver altså y som en funktion af x, som er defineret for alle reelle tal. Denne funktion har dog ikke et funktionsudtryk på analytisk form, altså med brug af elementære funktioner såsom polynomier, n’te rødder, trigonometriske funktioner, inverse trigonometriske funktioner, eksponentialfunktioner og logaritmefunktioner. Der er ikke en ”regneforskrift”, hvor man kan indsætte værdier af x og som giver den tilhørende y, men det er en glimrende funktion alligevel! Grafen er på Figur 4
“Anderledes aktiviteter”
Cykelruter
(Gymnasie)
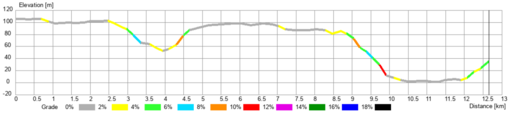
Eleverne får en profil af en cykelrute indtegnet i et koordinatsystem med højden som funktion af den vandrette afstand. De skal herefter skitsere cyklistens hastighed som funktion af den vandrette afstand. På Figur 5 er et eksempel uden akser og enheder.
Man kan bede eleverne overveje følgende:
- Hvad skal man vide om cyklisten for at lave denne skitse? (Bliver hun træt undervejs? Har hun en tophastighed på en vandret strækning? Skal hun stå af og trække, hvis det bliver meget stejlt?)
- Læreren kan give disse rammer først og derefter lade eleverne overveje, om der er andre muligheder, og om de vil ændre på skitsen.
- Kan man lave cykelrutens profil som funktion af den afstand, man har kørt? Hvordan vil det ændre grafen?
- Gymnasieelever med fysik A-niveau: Accelerationen afhænger af, hvor stejl ruten er, altså tangenthældningen. Find sammenhængen mellem tangenthældning og acceleration. Man kan begynde med en rute, hvor profilen er stykvis lineær.
Funktionsfabrikken.
(Grundskole, EUD, gymnasie)
Eleverne deles i grupper. Grupperne fabrikerer funktioner og bestiller funktioner hos de andre grupper. Læreren kan vælge selv at bestille funktioner for at illustrere pointer.
Bestillinger kunne være
- En funktion, der er lineær og hvis graf ikke skærer x-aksen
- En funktion, der skærer x-aksen i 3 forskellige punkter og y-aksen i ét punkt. Eleverne kan specificere, hvilke punkter, det drejer sig om.
- En funktion, der vokser mellem x = 2 og x = 6, aftager mellem x = 6 og x = 8.
- En funktion f, der vokser og opfylder f(0) = 2, f(3) = -2 (Det er ok med umulige funktioner.)
- En funktion, der har funktionsværdi 0 når -2 < x < 2 og funktionsværdi 7 ellers. (Hvis funktionsfabrikken ikke kan producere den, gøres eleverne opmærksomme på diskontinuerte funktioner.)
- En funktion f, der er konstant mellem x = -2 og x = 2.
Gruppen, der får bestillingen, kan
- Vælge at lave en graf for en funktion, der er som ønsket.
- Svare, at der ikke findes sådan en funktion.
- Overveje, om der er flere funktioner, der passer til kravene.
- Lave en forskrift
Grupperne, der bestiller, kan overveje
- Hvordan sikrer man sig, at fabrikken leverer det, man vil have – måske har gruppen selv tegnet grafen for det, der ønskes?
- Hvilke ord kan man bruge, når man bestiller – det vil afhænge af elevernes niveau.
Funktionsbyggeren
Denne aktivitet er hentet på https://undergroundmathematics.org/combining-functions/function-builder-i og https://undergroundmathematics.org/polynomials/function-builder-ii
Der er løsninger og mulighed for at printe et ark med mulige grafer, som eleverne kan matche til de forskellige felter.
Opgaverne omformer funktionsudtryk. Hvis man vil fremhæve at funktioner kan forstås som objekter, kan man skrive (a + b)(x) i stedet for a(x) + b(x) etc. Man kan anvende begge skrivemåder og lade eleverne overveje forskellen, måske er der ingen forskel for eleverne! Er det udfordrende for dem, at funktionerne ikke hedder, f, g, h?


Funktionsbyggeklodser
(Gymnasie)
Man vælger sig et antal funktioner af forskellig type som eleverne kender (konstante, lineære, 2.gradspolynomium, eksponentialfunktioner osv. Funktionerne kan været givet som grafer eller som forskrifter, og de kan være konkrete eller generelle.
Ud fra disse funktioner kan man nu bygge nye funktioner ved at addere, subtrahere, multiplicere etc. Eleverne skal opstille regler for, hvad der gælder for de nye funktioner som f.eks.:
- Hvis f og g er lineære, er f+g så lineær? Hvad med f·g?
- Hvad kan man sige om skæring med x-aksen for den nye funktion?
- Hvordan afhænger fortegnet for den nye funktion af fortegnet for funktionsbyggeklodserne?
- Kan man sige noget om f·g, hvis f er konstant? Hvis f og g er lineære?
- Kan man tage to lineære funktionsbyggeklodser, så f·g ikke har nogen rødder? Så toppunktet er et bestemt givet punkt?
emne: FUNKTIONER
UDGIVET: 2023