Eksempler på matematisk tankegangskompetence i gymnasiet
Disclaimer
På denne side er der opgaver, der gør brug af Ti-nspire. Ti-nspire filerne kan ikke findes på siden, men man er velkommen til at sende en mail til Mathilde (mkpedersen@ind.ku.dk), hvis man gerne vil have adgang til filerne.
De følgende eksempler stammer fra et forskningsstudie om matematisk tankegangskompetence i danske gymnasier, hvor det indholdsmæssige omdrejningspunkt var differentialregning og i særdeleshed definitionen af differentiabilitet, som introduceret i 2.g (Pedersen, 2024).
De fire aspekter af tankegangskompetencen og hvordan de kommer til udtryk hos eleverne er, som også nævnt i 'Hvad er matematisk tankegangskompetence?', ikke altid tydeligt opdelt. Det vil sige, flere af aspekterne kan godt komme i spil i samme opgave.
Opgaver om rækkevidden af rette linjer og hældning som introduktion til differentialregning
Opgaverne 1.1-1.4 nedenfor er designet med henblik på at rette elevernes opmærksomhed mod tankegangs-aspektet om begrebers rækkevidde (se Hvad er matematisk tankegangskompetence?) i forhold til hældningsbegrebet. Ideen var at bringe et velkendt begreb som hældning i spil med det formål at introducere eleverne til et nyt begreb om differentiabilitet. Dermed var hensigten, at eleverne kunne genkende begrebet hældning fra lineære funktioner og gøre brug af denne viden i en kontekst af ikke-lineære funktioner (Pedersen, 2024).
Opgave 1.1-1.4
-
Opgave 1.1)
Beskriv, hvad I forstår ved det matematiske begreb hældning. -
Opgave 1.2)
Vil I mene, at vi kan tale om hældning for ikke-lineære funktioner? I så fald hvorfor/hvorfor ikke og hvordan? -
Opgave 1.3)
Nedenfor ses grafen for en ikke-lineær funktion. Prøv på bedst tænkelig måde at bestemme hældningen til grafen for $x=5$.
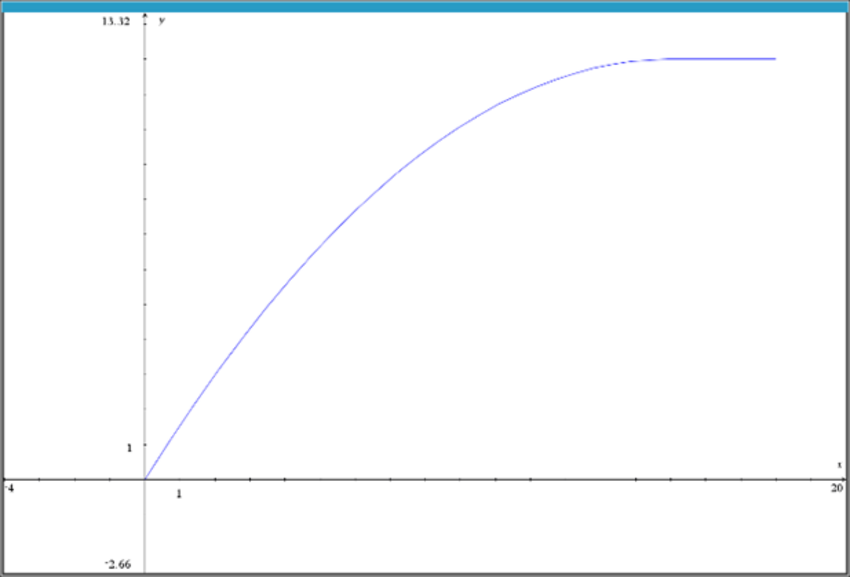
-
Opgave 1.4)
Nedenfor ses grafen for funktionen fra forrige opgave igen. Nu med en sekant, der går gennem to punkter $(x_0,f(x_0))$ og $(x_0+\Delta x,f(x_0+\Delta x))$.
Værdien for $x_0$ på $x$-aksen kan ændres ved at flytte på den tilhørende skyder x0.
Værdien $\Delta x$ kan ændres ved at flytte på den tilhørende skyder dx.-
Prøv nu med dette værktøj at bestemme hældningen for $x_0=5$.
-
Sæt $\Delta x = 0$ ved hjælp af den tilhørende skyder dx og giv et bud på, hvorfor sekanten forsvinder.
-
Overvej, hvorfor sekantens hældning kan skrives som $\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$.
-
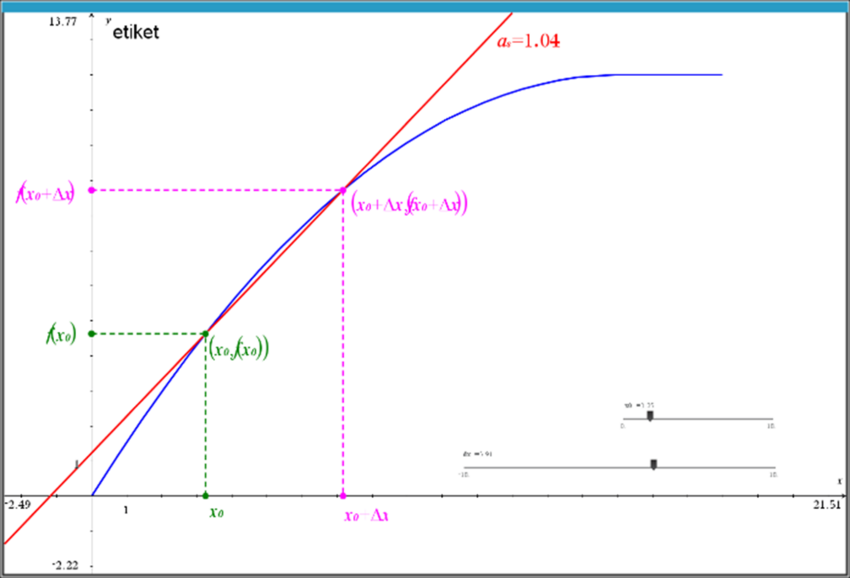
I ovenstående opgavesekvens begyndte mange af eleverne at diskutere begrebet hældning ved at repetere to-punktsformlen $\left(a=\frac{y_2-y_1}{x_2-x_1} \right)$, stille spørgsmål til hvorvidt en vandret linje har en hældning, og hvorvidt man kan finde hældningen til stykker af grafen og dermed dele grafen op i stykker eller intervaller, som de kendte det fra monotoniforhold. De undersøgte TI-nspire’s muligheder ved at indsætte en ret linje omkring $x=5$ eller indsætte en tangent, vha. tangentlinje-funktionen. Alt sammen bevægelser mod at bruge det, som de kendte om rette linjer og hældningsbegrebet til at undersøge denne ikke-lineære funktion. I Opgave 1.4 tog eleverne sig tid til at udforske de mange grafiske repræsentationer og oversætte mellem disse og opgaveformuleringen. Stort set alle elever fik ved hjælp af værktøjet estimeret sig frem til en hældning omkring $x=1,06$ og sammenlignet med den forrige opgave, hvilket gav mulighed for refleksion og diskussioner om, at jo tættere de to punkter er på hinanden, jo mere præcis kan man få hældningen.
Udover aspektet om begrebers rækkevidde som var intentionen, udviste eleverne også aspektet af spørgsmål og svar, i form af spørgsmål til hældningsbegrebet omkring lineære såvel som ikke-lineære funktioner, herunder hvilke svar der kan forventes i de to kontekster, samt en udvidelse af begrebet hældning fra konteksten om lineære funktioner til konteksten af ikke-lineære funktioner med brug af sekantbegrebet. På den måde kan opgaverne være med til at rette fokus mod aspektet omkring spørgsmål og svar til hældningsbegrebet og aspektet omkring hældningsbegrebets rækkevidde og udvidelsen til ideen bag differentiabilitetsbegrebet.
Opgaver om differentiabilitetsbegrebet med aspekter af tankegangskompetencen
Nedenfor præsenteres en række opgaver som inspiration til, hvordan man som underviser kan tænke tankegang ind i emnet om differentialregning, evt. med brug af dynamisk geometri og CAS.
Opgaverne er designet til, at elever kan arbejde med forskellige eksempler og ikke-eksempler af differentiabilitet. Ved at generalisere på baggrund af disse eksempler kan eleverne stille spørgsmål ved og overveje egenskaber og betingelser for, at en funktion er differentiabel i et givent punkt og i et interval (Pedersen, 2024).
De følgende opgaver går ud på, at eleverne undersøger sekanthældninger fra henholdsvis højre og venstre side af et punkt på grafen for en given funktion og dermed kan estimere en eventuel tangenthældning (i tilfælde af, at den eksisterer). Det vigtige er her, at eleverne kan overveje, hvornår det er muligt at give et bud på en tangenthældning, og hvornår det ikke er, samt hvornår hele funktionen har egenskaben ”at være differentiabel”. Hermed er det hensigten, at eleverne kan arbejde med spørgsmål og svar om differentiabilitet, betingelser for differentiabilitet samt med definitionen af differentiabilitet og dennes matematiske opbygning.
Disse opgaver gør alene ikke, at eleverne arbejder med ”eksistens” og ”for alle” eller begynder at udvide deres begreb om differentiabilitet. Står opgaven alene, kan den derimod give nogle forkerte opfattelser, som at tangenthældningen er noget man konstruerer, frem for undersøger eksistensen af. Opgaven er tænkt som en del af en sekvens, hvor arbejdet med definitionen af differentiabilitet er i fokus. Dette kan ses fx i modsætning til en eventuel algoritmisk introduktion af tretrinsreglen som en guide til, hvordan man beviser sætninger for bestemmelse af differentialkvotienter af elementære funktioner. (Pedersen, 2024).
Opgave 2 – differentiabilitet og tankegangskompetence
I denne opgave er tanken, at eleverne arbejder med de grafiske repræsentationer af, at differenskvotienten går mod differentialkvotienten, når afstanden mellem $x$-værdierne går mod $0$. Her angivet ved en type notation:
$\frac{f(x_0+ \Delta x)-f(x_0)}{\Delta x} \to A \text{ for } \Delta x \to 0$
Opgave og løsning
- Nedenfor ses grafen for funktionen $f$, som er givet ved forskriften:
$f(x) = \begin{cases} \frac{1}{15}x^3-2x^2+5,4x+1,8 \quad -0,5 \leq x \leq 9 \\ \qquad \qquad \qquad \qquad \quad 1,8 \qquad \text{ }9 < x \leq 15 \end{cases}$
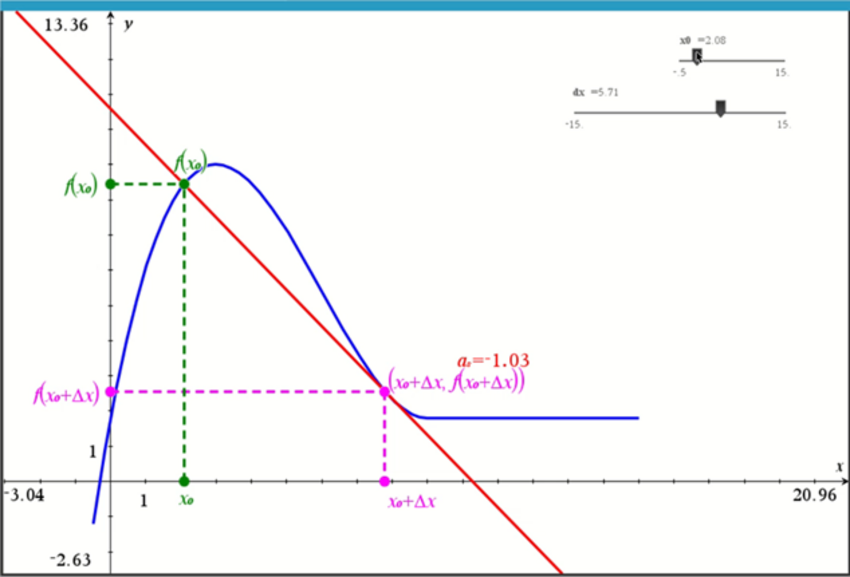
-
Undersøg ved hjælp af sekanten om funktionen er differentiabel i $x_0=1$, $x_0=3$ og $x_0=9$.
-
Vurder om funktionen er differentiabel i hele intervallet $]-0,5;15[$.
Løsning: Funktionen er differentiabel for alle tre værdier $x_0=1$, $x_0=3$ og $x_0=9$, og eftersom den er differentiabel i $x_0=9$, er den også differentiabel i hele intervallet.
Elevdiskussioner i forbindelse med opgave 2
I følgende elevdiskussion har to elever (L og K) løst opgave 2.a) og fundet, at funktionen er differentiabel i alle tre angivne værdier. De går herefter til opgave 2.b), hvoraf følgende er et uddrag af deres diskussion af at løse denne opgave.
Elevdiskussion 1
L: Altså, når det er en gaffelfunktion, så tror jeg ikke den er differentiabel i hele intervallet.
ㅤ
K: Jaa... Så er der et knæk. […] Men hvordan skal vi undersøge, om den er differentiabel i hele intervallet? Skal vi så sætte alle tallene ind?
Tegn på tankegangskompetence
- Elev L har en formodning om, at egenskaben ”at være en gaffelfunktion” er en tilstrækkelig betingelse for ikke-differentiabilitet, hvilket viser aspekterne om begrebers rækkevidde og matematiske udsagn.
- Elev K omsætter egenskaben ”at være en gaffel-funktion” i den symbolske repræsentation til egenskaben ”at have et knæk” i den grafiske repræsentation, hvilket er en del af aspektet om begrebers rækkevidde.
Derudover ses det, at elev K fortolker den implicitte universal-kvantor i udtrykket ”hele funktionen” til handlingen ”at sætte alle tallene ind.” Dette viser aspektet om matematiske udsagn.
ㅤ
Eftersom L og K godt kan se umuligheden af den handling, spørger de deres underviser om hjælp. De forklarer, at de tror, at funktionen ikke er differentiabel, fordi det er en gaffelfunktion, og at der derfor også må være et knæk, men samtidig at de i deres tidligere undersøgelse har fundet ud af, at den givne funktion er differentiabel i $x=9$, hvor de ellers ville forvente et knæk.
U: Ja, den er stadig differentiabel i knækket […] der er så glidende en overgang fra den første del til den anden, at der faktisk ikke er noget knæk, på trods af ændringen i funktionsudtrykket.
ㅤ
L: Okay. Så den er differentiabel... eller den er differentiabel, fordi overgangen i knækket er så god... eller noget.
- Underviseren bekræfter hermed differentiabilitet i det kritiske punkt, men afviser samtidig K’s formodning om ikke-differentiabilitet. Underviseren forklarer sammenhængen mellem funktionsudtryk, det grafiske knæk og hvorfor egenskaben ”at være en gaffelfunktion” ikke er en tilstrækkelig betingelse for at udlede ikke-differentiabilitet.
- Tøvende ændrer Elev L sin formodning om ikke-differentiabilitet og gør plads til at udvide begrebet om differentiabilitet som en egenskab også for gaffelfunktioner. Dette viser aspektet om begrebers rækkevidde.
I det følgende har to andre elever (E og F) også løst opgave 2.1 a) og fundet, at funktionen er differentiabel i alle tre værdier. Da de går til opgave 2.1 b) bliver de udfordret på, hvordan de skal betragte differentiabilitet af en funktion.
Elevdiskussion 2
F: ...Så kan vi bare sætte alle ind [begynder at grine]
ㅤ
E: Okay, med alle punkter? Alle uendelige punkter [griner].
F: Nej, ej, jeg ved ikke. […] Men jeg forstår det ikke. Vil der ikke altid være mindst et punkt som er differentiabel?
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
ㅤ
E: Jo, det tror jeg. Så man kan ikke sige, om en funktion er differentiabelㅤ
ㅤ
ㅤ
F: Men så igen. Det tror jeg altså, man kan. Jeg forstår det ikke, om hele funktionen er differentiabel.ㅤ
Tegn på tankegangskompetence
- Som i de forrige eksempler, ses her, hvordan elev F fortolker ”alle”-kvantoren til handlingen ”at sætte alle tallene ind”, hvilket igen er aspektet om matematiske udsagn.
- Elev E gør her opmærksom på absurditeten i denne umulige handling.
- Dette kan elev F godt følge, hvilket leder frem til, at hun udtrykker sin forvirring omkring, hvordan de kan tale om, at en funktion er differentiabel.
Elev F’s spørgsmål ”Vil der ikke altid være mindst et punkt som er differentiabel?” tyder på, at hun ser differentiabilitet som en egenskab for et punkt på en funktion, og ikke som en egenskab for hele funktionen, hvilket primært er aspektet om begrebers rækkevidde, men det indeholder også aspekterne om spørgsmål og svar, samt matematiske udsagn. Derudover indikerer spørgsmålet også, at elev F forsøger at generalisere på baggrund af de eksempler, de har arbejdet med, hvilket er en del af aspektet om abstraktion og generalisering.
Eleverne har i denne opgavesekvens kun arbejdet med differentiable og stykvis-differentiable funktioner, som netop alle indeholder mindst et punkt, der vil være differentiabelt. - Elev E understøtter F’s undren med formodningen om, at differentiabilitet ikke er en egenskab tilknyttet funktionsbegrebet, hvilket igen er tilknyttet aspektet om begrebers rækkevidde, men også aspekterne om matematiske udsagn og spørgsmål og svar.
- Vi ser altså, at eleverne E og F har svært ved at udvide begrebet om differentiabilitet fra at beskrive enkelte punkter til at beskrive en hel funktion, hvilket hører under aspektet om begrebers rækkevidde.
Fordele og ulemper ved opgave 2
Opgaven giver mulighed for at tale om eksistensbegrebet af tangenthældningen og dermed også af differentialkvotienten. Derudover arbejder den med udvidelsen af at afgøre, om en funktion er differentiabel i et enkelt punkt til at se det som en egenskab for hele funktionen. Dette er et ret abstrakt og vigtigt skridt, når vi arbejder med beviser for differentiabilitet af elementærfunktioner. Denne udfordring ses også hos de to elevpar, som begge stiller spørgsmålet om, hvordan man undersøger en hel funktion. Her vil det være en god idé at udvikle på den samtale underviseren her har med L og K og tale videre om, hvordan man undersøger hele funktionen.
Modsat forsvinder grænseværdibegrebet i denne opgave. Selv om eleverne kan arbejde med variablen $\Delta x$ og dermed undersøge, hvad der sker, når $\Delta x$ går mod 0, så tastede flere af eleverne blot to værdier ind (som fx $\Delta x = -0,001$ og $\Delta x =0,001$) og aflæste, om sekanthældningen gav det samme i de to tilfælde. Hermed bliver tangenthældningen i højere grad noget man konstruerer, fremfor undersøger eksistensen af. Dette prøver næste opgave at tage højde for, hvor eleverne skal udfylde et skema med sekanthældninger for forskellige værdier af $\Delta x$ og derfra vurdere, om tangenthældningen eksisterer.
Opgave 3 – ikke-differentiabilitet og tankegangskompetence
Som nævnt, idéen med den følgende opgave er at få eleverne til at arbejde med konvergens mod en (eventuelt eksisterende) tangenthældning (altså mod en grænseværdi). Ideen er, at eleverne ved små skridt nærmer sig det pågældende punkt og betragter, hvordan sekanthældningen ændrer sig for hvert lille skridt. På denne baggrund skal de så vurdere, hvilket tal disse sekanthældninger nærmer sig, og om dette er det samme tal, når de nærmer sig fra henholdsvis højre og venstre. Hensigten med opgaven er at få eleverne til at undre sig og stille spørgsmål til hvilke betingelser, der skal være opfyldt, for at en funktion er differentiabel i et givent punkt. Derudover er det på længere sigt hensigten at udvide begrebet til differentiabilitet af en samlet funktion.
Opgave og løsning
Nedenfor ses grafen for funktionen $f$, som er givet ved
$f(x)= \begin{cases} ㅤㅤㅤㅤㅤㅤㅤㅤ(x+3)^2-2,4 \quad -6 < x \leq -4 \\ -0,1 \cdot (x+5) \cdot (x+2) \cdot (x-3) \quad -4 < x \leq 1 \\ ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ\quad 3,6 \qquad 1 < x < 6 \end{cases}$
Derudover ses en sekant, der skærer grafen i de to punkter $(x_0,f(x_0))$ og $(x_0+\Delta x,f(x_0+ \Delta x))$ samt sekanthældningen $a_s$.
Værdien for $x_0$ på $x$-aksen kan ændres ved at flytte på den tilhørende skyder x0, og værdien $\Delta x$ kan ændres ved at flytte på den tilhørende skyder dx.
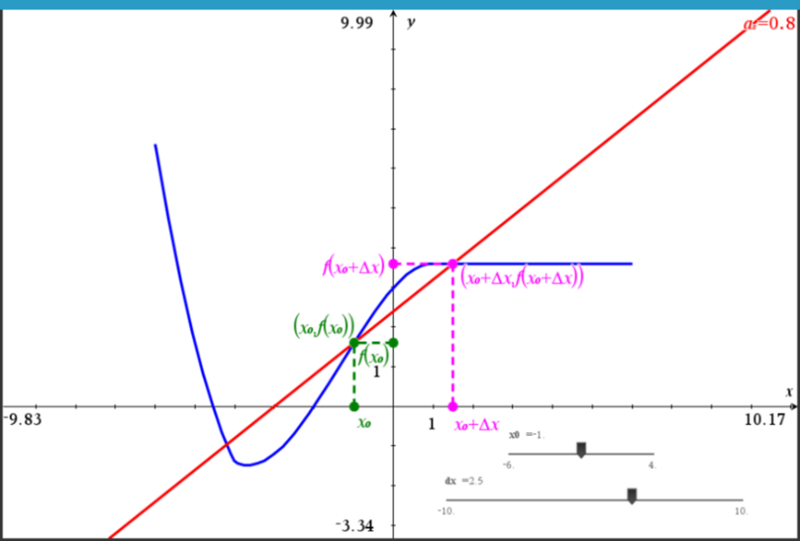
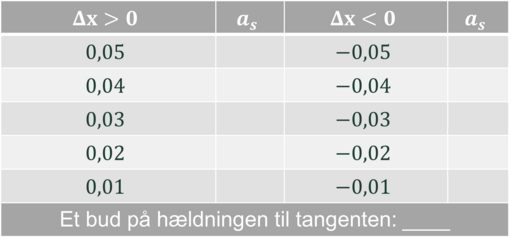
a) Udfyld tabellen til højre for $x_0=-1,5$ og giv et bud på, hvad hældningen til tangenten i $x_0$ kunne være.
b) Lav en tilsvarende tabel for $x_0=1$ og $x_0=-4$, hvor I selv bestemmer værdierne for $\Delta x$ og giv et bud på, hvad hældningen til tangenten kunne være i disse tilfælde.
Løsning:
I opgave a) er funktionen differentiabel for $x=-1,5$ og har en tangenthældning i punktet på $1,625$. I opgave b) er funktionen differentiabel for $x=1$, hvor tangenthældningen er $0$. Derimod er funktionen ikke differentiabel for $x=-4$, hvor sekanthældningen går mod $-2$ fra venstre og $-0,5$ fra højre.
Særligt eksemplet af ikke-differentiabilitet i et punkt får eleverne til at opstille små hypoteser omkring, hvornår noget er differentiabelt og hvornår det ikke er, før de er blevet præsenteret for en formel definition af differentiabilitet.
Elevbesvarelse af opgave 3

I tabellen til højre ses to elevers (O og P) besvarelse af opgave b) for $x_0=-4$.
Besvarelsen i tabellen er skrevet over flere omgange. Først indtastede de alle sekanthældningerne for $\Delta x > 0$ og vurderede, at det gik mod $-0,5$.
Dernæst indtastede de sekanthældninger for $\Delta x < 0$ og vurderede, at det gik mod $-2$. Hvortil de opstillede følgende hypotese:
"Det, der sker er, at det ene går mod én ting, og det andet går mod noget andet. Så jeg tror meget nemt, vi kan sige, at den ikke er differentiabel."
Derefter skrev de nede i nederste celle:
"Hældningen til tangenten kan både være $0$ og $-2$. Derfor er vores funktion ikke differentiabel i alle punkter og har ikke en tangent i det pågældende punkt. Hele funktionen er kontinuert”
(I deres snak havde de diskuteret, at sekanthældningerne gik mod $-0,5$, men skrev kun $0$ i deres besvarelse.)
Senere blev de introduceret til eksistensen af tangenthældingen og den symbolske notation, hvorefter de gik tilbage til denne opgave og skrev:
"$a_0$ eksisterer ikke."
Elevdiskussion i forlængelse af opgave 3
Efterfølgende, som en gennemgang og generalisering af deres arbejde (se Matematisk tankegang i forskellige faser af matematisk arbejde), forsøgte særligt eleven P at opstille hypoteser for ikke-differentiable funktioner og dermed udvide sit begreb om ikke-differentiable funktioner.
Da de havde løst opgave 3 og ville formulere et svar, spurgte eleven P underviseren, om de havde forstået det rigtigt, hvorefter samtalen med underviseren yderligere udviklede sig:
Elevdiskussion med underviseren
P: Så ved en ikke-differentiabel funktion kan man finde tangenten til nogle punkter. Det er bare ikke altid, man kan det.
U: Så hvis du har en funktion, der ikke er differentiabel, kan den være stykvis differentiabel. Der kan være punkter, hvor den er differentiabel, men der vil være ét punkt, hvor den ikke er differentiabel.
P: Det vil sige, du kan faktisk altid, for enhver funktion vil der være et eller andet sted, hvor den er differentiabel?
ㅤ
U: Faktisk er der funktioner, der er alle steder kontinuerte, men ingen steder differentiable.
P: Som er totalt hakket. Men skal den så ikke være uendeligt hakket?
ㅤ
ㅤ
U: Jo. […] Prøv at google det.
De to elever P og O prøver at google det, men får kun resultater, der viser stykvist differentiable funktioner. Da dette ikke var, hvad de ledte efter, hjalp underviseren dem ved at slå Weierstrassfunktionen op.
Tegn på tankegangskompetence
- Elev P’s forsøg på at generalisere, hvad en ikke-differentiabel funktion er på baggrund af eksemplet, hvilket hører under aspektet om abstraktion og generalisering.
ㅤ - Underviseren uddyber her begrebet stykvis differentiabel og understreger eksistensen af et punkt, der ikke er differentiabelt.
ㅤ
ㅤ
ㅤ - Elev P formulerer en general hypotese over alle funktioner på baggrund af underviserens udlægning, og forsøger hermed at formulere et universal-udsagn. Dette hører under aspekterne abstraktion og generalisering samt matematiske udsagn.
- Underviseren afviser denne hypotese ved at påpege, at der findes et modeksempel til, at alle funktioner er stykvis differentiable.
- Elev P kæder ikke-differentiabilitet sammen den grafiske repræsentation af en funktion er hakket og kan på den måde forestille sig den ingen-steder differentiable funktion, hvilket er den del af begrebers rækkevidde inden for forskellige kontekster.
- Hermed udvidede eleverne deres begreb om differentiabilitet, fra differentiabilitet i et enkelt punkt, til at en funktion kan være stykvis differentiabel, og til sidst til at den kan være ingen steder differentiabel, hvilket hører under aspektet om begrebers rækkevidde. Denne proces og diskussion inddrog også andre elever og pirrede deres nysgerrighed.
Fordele og ulemper ved opgave 3
Opgaven kan fungere som introduktion til eksistensbegrebet i relation til differentialkvotienten i et punkt, samt til en diskussion om for alle i relation til differentiabilitet af en funktion, før definitionen af differentiabilitet og differentialkvotienten introduceres.
Den givne funktion er ikke differentiabel for $x=-4$, hvilket kan give eleverne en idé om forskellen på, hvornår differentialkvotienten i et punkt eksisterer, og hvornår den ikke gør. Derudover kan denne funktion sammen med en funktion, der er alle steder differentiabel, initierer diskussioner om ”for alle $x$ i domænet”, så som hvordan man undersøger ”for alle $x$” og negationen af ”for alle” og sammenhængen med eksistensen af et modeksempel.
Andre relevante spørgsmål til en funktion som $f$ er: For hvilke værdier er det interessant at undersøge funktionen, og hvorfor? Hvilke typer funktioner består den samlede funktion af? Hvad betyder domænet og sammensætningen af domænet for funktionsudtrykket?
I opgaven er de to variable punkter angivet ved de generelle udtryk $(x_0,f(x_0))$ og $(x_0+\Delta x,f(x_0 + \Delta x))$. Det er dog vigtigt at bemærke, at i opgaven arbejder eleverne med disse to udtryk i form af konkrete eksempler. De to variable $x_0$ og $\Delta x$ kan justeres og dermed eksemplificeres. Det kan være en god idé at arbejde med disse eksempler i flere skridt ved fx først at holde $x_0$ fast og kun ændre på tilvæksten $\Delta x$, som det også ses i opgaveformuleringen.
Overgangen fra at arbejde med konkrete eksempler til en forståelse af de generelle begreber som sekant og sekanthældning er ofte vanskelig for eleverne. Derfor er det vigtigt at underviseren giver eleverne et godt erfaringsgrundlag at bygge deres begrebsdannelse på (Se også At eksemplificere og generalisere i forbindelse med matematiske begreber).
Derudover er det vigtigt at tage højde for antallet af decimaler, der angives i sekanthældningen. Med for få decimaler kan det være svært at se en forskel på sekanthældningerne for de forskellige værdier af tilvæksten $\Delta x$ og dermed svært at give et kvalificeret bud på en eventuel tangenthældning. Prøv fx at løse opgave a) for henholdsvis to decimaler og seks decimaler.
For eksempel var der også elever, der tog gennemsnittet af den sidste sekanthældning fra henholdsvis højre og venstre, hvilket ikke virker. Denne fejl kan være med til at give en opfattelse af, at vi konstruerer tangenthældningen frem for, at vi undersøger, om den eksisterer, ligesom vi så det i den forrige opgave.
Et alternativ til computeropgaver
Funktionerne i de forrige opgaver er meget grimme og svære at gå til uden en computer. Hermed er det computerens svar, der bliver afgørende for, om eleverne kan udlede differentiabilitet eller ikke-differentiabilitet.
Som alternativ kan eleverne arbejde med mere velkendte funktionsudtryk, som pæne lineære funktioner og andengradspolynomier, der er sat sammen til nemmere tilgængelige gaffelfunktioner, som eleverne har bedre mulighed for at regne på uden brug af computer.
til: GYMNASIER
emne: MATEMATISK TANKEGANG
UDGIVET: 2025