Hvad er matematisk tankegang?
Begrebet matematisk tankegang defineres sjældent eksplicit, og hvad det dækker over varierer i matematikdidaktisk forskningslitteratur, om end det ofte har udgangspunkt i forskellige sammensætninger af matematiske praksisser, såsom matematisk ræsonnement, problemløsning, modellering, abstraktion, symbolmanipulation samt at håndtere repræsentationer (fx Drijvers et al., 2019, National Research Council, 1989).
Matematisk tankegang i forskellige faser af matematisk arbejde
En måde at karakterisere matematisk tankegang på er som en samling af de arbejdsprocesser, der er nødvendige for at håndtere matematiske spørgsmål og problemer. Dette indbefatter dualiteterne:
-
at specialisere og generalisere
-
at formode/opstille formodninger og overbevise sig selv og andre
-
at forestille sig og udtrykke sig
-
at udvide og at afgrænse et begreb
-
at klassificere og at karakterisere situationer og begreber (Mason et al., 2010).
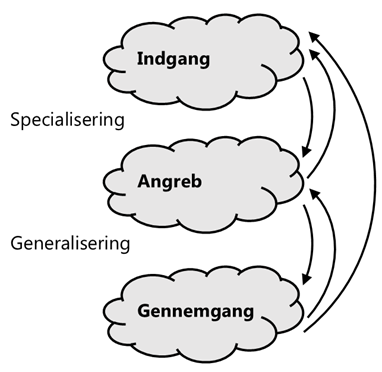
Disse processer kommer i spil under tre faser af matematisk arbejde illustreret i Figur 1, som her er oversat til indgang (entry), angreb (attack), og gennemgang (review).
-
Indgangsfasen handler om at forstå spørgsmålet, gøre det til sit eget og overveje arten af det svar, der kræves for at besvare spørgsmålet eller løse problemet. Spørgsmål, der indgår som en del af indgangsfasen, er: Hvad får jeg at vide? Hvad vil jeg gerne finde ud af? Hvad vil jeg gerne gøre? Og hvilken viden kan jeg benytte mig af?
-
Angrebsfasen begynder, når udøveren annammer spørgsmålet, og det dermed er blevet ens eget. Fasen indeholder løsningsforsøg og udøvelse, og dermed at implementere strategier, afprøve eksempler, ændre på betingelserne, mønstergenkendelse, opsætte formodninger og prøve dem af, samt overbevise sig selv og andre om sine strategier, løsninger og generaliseringer. Fasen slutter, når problemet er løst eller opgivet.
-
Gennemgangsfasen er at se tilbage og reflektere over løsningen og de strategier, der er brugt i angrebsfasen, samt at udvide spørgsmålet til nye sammenhænge eller domæner. Elementer i denne fase er at kontrollere, om svar og spørgsmål stemmer overens, at reflektere over nøgleideer og nøgleøjeblikke i løsningsprocessen, samt at udvide spørgsmål og svar til nye eller bredere sammenhænge.
Ovenstående beskrivelse af matematisk tankegang kan opfattes ret konkret, fordi faserne giver mulighed for at opdele arbejdet og gøre det mere håndgribeligt. Gennemgangsfasen bliver dog tit udeladt eller glemt, da opgaven ofte er løst forud for denne fase. Dog er gennemgangsfasen et vigtigt element i matematisk tankegang og for forståelsen af matematisk arbejde og undersøgelse (Mason et al., 2010). En måde at fastholde vigtigheden af gennemgangsfasen på er at lægge vægt på abstraktion og generalisering og dermed på udvidelsen af det givne problem samt af den løsning, der blev fundet i angrebsfasen.
Ved at lave forskellige aktiviteter, der har fokus på de forskellige faser og fremhæve de spørgsmål, der hører til hver fase, kan man som underviser tydeliggøre de tre faser for eleverne. For eksempel kan eleverne diskutere i grupper og i klassen de fire hv-spørgsmål, der hører til indgangsfasen. Dette kan ses som en isoleret aktivitet uden fokus på angrebsfasen. Tilsvarende kan man i gennemgangsfasen bede eleverne dele deres strategier fra angrebsfasen. Således kan de diskutere hvilke strategier, der fører til hvilke resultater. Derudover kan eleverne drøfte opgavens form og resultat, hvis de skulle stramme, slække, fjerne eller tilføje betingelser for den givne opgave.
Avanceret matematisk tankegang
En anden måde at karakterisere matematisk tankegang er ved at præcisere det til avanceret matematisk tankegang (Tall, 2002). Dette består også af en lignende række aktiviteter, der går fra at betragte et problem til at formulere formodninger og til slut forfine og bevise disse. Avanceret matematisk tankegang har også tilknyttet en række arbejdsprocesser såsom at repræsentere og håndtere repræsentationer af matematiske begreber samt modellering, generalisering og abstraktion. Avanceret matematisk tankegang forbindes ofte også til ”the big ideas” i matematikken, som fx infinitesimalregningen. Derudover hører det også til avanceret matematisk tankegang at kunne forene og organisere fakta, definitioner, regneregler, sætninger, eksempler og opgaver m.m., som hører til et givent område og dermed danne et samlet billede af et matematisk emne (Dreyfus, 2002).
Forskellen på avanceret matematisk tankegang i forhold til det forrige perspektiv—der kan kaldes elementær matematisk tankegang— består i, at avanceret matematisk tankegang i højere grad angår at formalisere aspekter af matematikken. Det kan være ved at definere begreber frem for at beskrive dem, og ved at bevise på en logisk måde baseret på definitioner frem for at overbevise (Tall, 2002). Præcis denne skelnen er essentiel for gymnasiets tre niveauer af matematik (hhv. A, B og C-niveau). For eksempel, jo højere niveau, jo mere fylder beviser og matematisk ræsonnement, struktur og opbygning. Tydeligt bliver det også i forbindelse med introduktionen til differentialregning, hvor der ofte bliver gjort mere ud af definitionen af differentialkvotient med henvisning til begreberne kontinuitet og grænseværdi på A-niveau i forhold til på B-niveau.
Formalisering som en del af matematisk tankegang
Både i såkaldt elementær og avanceret matematisk tankegang er generalisering og abstraktion vigtige elementer. Dette genfindes også i andre opfattelser af matematisk tankegang. For eksempel, en tredje definition af matematisk tankegang er at se det som en triade bestående af problemløsning, modellering og abstraktion. En vigtig pointe i denne triade er, at matematisk tankegang ikke kan reduceres til en af disse alene. Alligevel er abstraktion helt central for dette syn på matematisk tankegang, fordi det handler om at generalisere og finde mønstre og lighedspunkter på tværs af eksempler, som ofte behandlet gennem problemløsning og modellering (Drijvers et al., 2019).
Når vi i matematik generaliserer over en samling eksempler, kan det ofte formuleres som konkrete formodninger eller nye spørgsmål. Undervejs i arbejdet med matematik skal det oprindelige spørgsmål og de involverede begreber ofte relateres til relevante definitioner og andre matematiske udsagn. I den forbindelse kan det være nødvendigt at navigere med logiske operatorer (implicitte såvel som eksplicitte) (Mason et al., 2010).
Matematik er karakteriseret ved sin opbygning med aksiomer, definitioner, sætninger, beviser, formodninger, og eksempler, samt ved sammenspillet mellem dem. Disse forskellige typer udsagn omhandler matematisk definerede begreber. Arbejdet med disse udsagn i detaljer giver mulighed for at beskæftige sig med essentielle operatorer, såsom entydighed, eksistens og universale påstande. Disse betyder meget for måden vi tænker på i matematik—og dermed også for hvordan vi i matematik undersøger, ræsonnerer, beviser og gør brug af eksempler og repræsentationer.
Matematisk tankegang dækker meget bredt og er ofte beskrevet ud fra problemløsning, ræsonnement, modellering, håndtering af symboler og repræsentationer, generalisering og formalisme. I modsætning hertil er tankegangskompetencen, som den er beskrevet i KOM-rapporten (se Hvad er matematisk tankegangskompetence?), adskilt fra ræsonnement, problembehandling, modellering, formalisme og symbolbehandling, samt fra håndtering af repræsentationer.
til: GYMNASIER
emne: MATEMATISK TANKEGANG
UDGIVET: 2025