Aktivitet og forløb: At folde en kasse af papir
Dette forløb benyttes som brobygningsaktivitet i gymnasiet for elever fra 8.-10. klassetrin. Når forløbet bruges i grundskolen, kan fokus være på opstilling af regneudtryk for et konkret rumfang og generalisering til opstilling af en formel fra en kontekst. I gymnasiet kan man fokusere på opstilling af formler for fx rumfang og overfladeareal fra konteksten, og hvordan disse kan opfattes som variabelsammenhænge.
Forløb
Dette forløb er en beskrivelse af et brobygningsforløb afholdt i en 9.-klasse.
Varighed: 1 modul
Materialer: saks, papir/karton, tape, tegneprogram som fx GeoGebra.
- Iscenesættelse: Eleverne fik flere stykker papir/karton i A4-format (21cm x 29,7 cm), og blev bedt om at folde en kasse. For de elever, der havde svært ved at forstå hvordan det kunne lade sig gøre, havde læreren et GeoGebra-dokument, som kunne vise foldning af kassen i forskellige stadier.
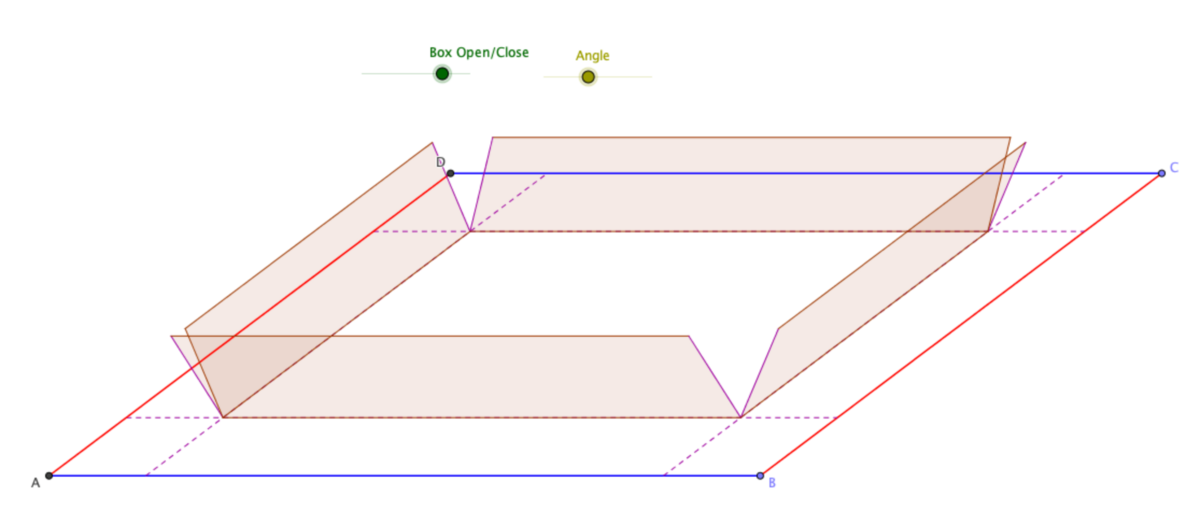

- Lærerens indledende spørgsmål:
Hvor stort er rumfanget af den kasse, I har foldet?
Fold en anden kasse. Hvor stort er rumfanget nu? - Elevernes selvstændige arbejde:
Eleverne gik i gang med at klippe og folde kasser. De arbejdede i grupper og fordelte de forskellige kasser mellem sig. Herefter beregnede de rumfanget af de foldede kasser, hvor de havde foldet siderne, fx 1, 2, 3, … cm op.
Hurtigt opdagede nogle af eleverne, at man ikke kan folde en side mere end halvvejs op, så det (heldigvis!) var begrænset, hvor mange kasser der skulle foldes.
Alle grupper fik af egen drift skrevet regneudtryk op til bestemmelse af rumfanget, så de nemt kunne beregne det for forskellige kasser ved bare at indsætte forskellige værdier af kantens højde. Et par grupper benyttede regneark til at finde rumfanget for alle kasser med heltallig højde. - Næste fase og flere mulige problemstillinger: Da grupperne arbejdede med meget forskellig hastighed, var det nødvendigt at bruge tid på at hjælpe nogle grupper og give andre flere udfordringer. Læreren fik sat gang i undersøgelser af optimering af kassens rumfang: "Hvilken af jeres kasser kan rumme mest?", og bestemmelse af deres overfladeareal. En enkelt gruppe fandt på at undersøge forholdet mellem overfladeareal og rumfang.
- Afslutning: Timen sluttede af med en diskussion af, hvordan man finder det største rumfang. De fleste grupper havde tegnet sammenhørende værdier af kassernes højde og deres rumfang ind og kunne tilnærmelsesvist aflæse det maksimale rumfang ved punkt D (se figuren nedenfor).
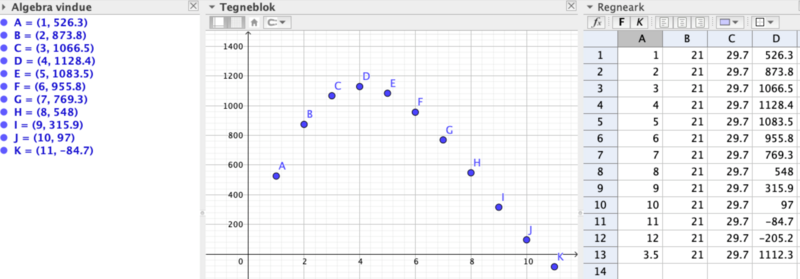
En gruppe foreslog, at man også skulle tegne "grafen for formlen $V= x(21-2x)(29,7-2x)$". Denne formel var det regneudtryk, eleverne havde formuleret tidligere, og spørgsmålet førte til en diskussion af forskellen på en formel og en funktion, hvor også definitionsmængde blev inddraget. Bestod den af heltal eller af reelle tal? Og hvilke?
Ved at tegne funktionen $f(x) = x·(21-2x)·(29,7-2x) = 623,7·x – 101,4·x^2 + 4·x^3$ ind sammen med punkterne, blev det klart, at $D$ ikke var den helt rigtige værdi.
Ved hjælp af GeoGebra kunne det største rumfang aflæses ved punktet $L$. Endelig blev eleverne bedt om at beskrive, hvad der gjorde punktet $L$ til noget særligt. Hvordan adskiller det sig fra de andre punkter på grafen? Her kom mange bud, og en gruppe bemærkede, at hvis man tegnede en vandret linje over grafen, og lod den bevæge sig nedad, ville det være i $L$, at den første gang ramte grafen. Dette er en måde at formulere, at der er en vandret tangent i $L$, og hermed er vejen for indførelsen af differentialregning åbnet, men nok ikke brobygning!
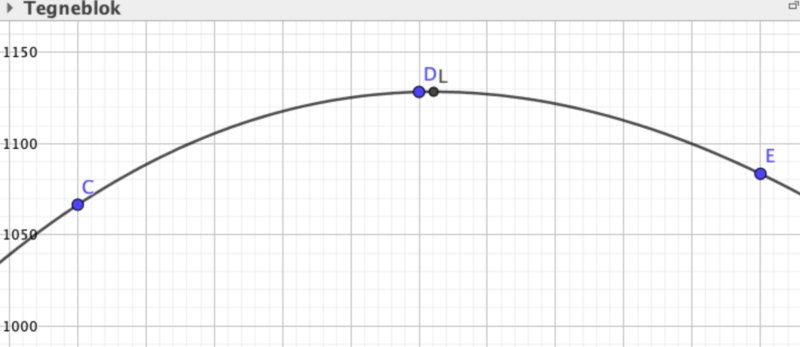
-
Læringsudbytte: Som ovenstående beskrivelse antyder, kan selv et meget kort forløb, der nok synes enkelt og lige til, føre til inddragelse af mange af algebraens aspekter:
-
Fra beregninger på konkrete tal til opstilling af et generelt udtryk (formel) herunder at indføre symboler for ukendte størrelser.
-
Sammenhæng mellem formel og funktion herunder beregning/omformning af algebraisk udtryk, nemlig $x·(21-2x)·(29,7-2x) = 623,7·x – 101,4·x^2 + 4·x^3$ for at få en 'rigtig' funktionsforskrift $f(x) = 623,7·x – 101,4·x^2 + 4·x^3$.
-
Definitionsmængde for funktioner og forskellen på hele og reelle tal.
-
Påbegynde arbejdet med at finde største og mindsteværdier for funktioner (vandret tangent) som grundlag for senere at indføre differentialregning.
-
TIL OVERVEJELSE I FAGGRUPPEN
- Diskutér hvad eleverne får mulighed for at lære ved et forløb som dette?
- Hvordan kan forløbet udbygges med flere aktiviteter for at forøge læringsudbyttet på det niveau, I underviser på?
til: GRUNDSKOLE & GYMNASIE
emne: ALGEBRA
UDGIVET: 2021