Hvad er skolealgebra?
Hvor man i aritmetikken regner på tal, kan algebra meget kort beskrives som "bogstavregning". Oprindelig blev algebra betragtet som generaliserede beregninger, og dermed følger alle de grundlæggende regneregler, som vi kender fra regning med tal. Fx er faktorernes orden ligegyldig ved multiplikation, og man kan gange ind i parenteser – den distributive lov – når man regner med bogstaver. Læs her om algebraens mange ansigter, illustreret med konkrete eksempler.
Algebra er mere end regning med bogstaver
Men algebra er meget mere end bogstavregning. For det første giver algebra os nemlig værktøjet til at udtrykke sammenhænge på en præcis og håndterbar måde. Sådanne sammenhænge kan være et resultat af matematisk modellering, hvor de fx beskriver situationer fra den virkelige verden. Det kan også være en abstrakt matematisk sammenhæng, som er repræsenteret ved et symbolsk udtryk, et mønster, en tabel eller en graf. Med algebra bliver det muligt at udforske egenskaber ved sådanne sammenhænge, som ofte kun er gennemskuelige i den symbolske repræsentationsform.
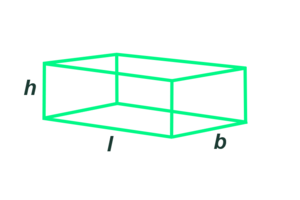
For det andet bruger vi algebra til at generalisere beregninger, når vi indfører formler. Tænk på en kasse med længden $l$, bredden $b$ og højden $h$. Kassen har rumfanget $V = l \cdot b \cdot h$. Uden denne formel må vi ved hver kasse, som vi ønsker at finde rumfanget for, argumentere for beregningen. Men når vi én gang for alle har argumenteret for formlens rigtighed, kan vi blot sætte tal ind for længde, bredde og højde i alle nye kasser, vi skal finde rumfanget for. (Kilde 1)
Men selvom algebra indgår i mange områder af matematikundervisningen, er det svært at finde en præcis definition af, hvad man mener, når man taler om algebra i grundskole og gymnasiet. Elementer som omformninger af bogstavudtryk, generalisering af numeriske og geometriske mønstre, opstilling af formler, der beskriver forholdet mellem variable størrelser, samt at ræsonnere matematisk indgår dog tit. I nogle beskrivelser går man endnu længere og medtager også arbejdet med funktioner og deres repræsentationer, ja sommetider medtager man også mere generel problemløsning og modellering af matematiske og virkelighedsnære fænomener. (Kilde 1)
Se også afsnittet om 'algebraisk tænkning' i temaet om Algebra på de yngste klassetrin.
Eksempler
Der er mange forskellige formål med at lave algebra (doing algebra), de kan bedst illustreres med en række eksempler:
1. At generalisere
Når man taler om at udtrykke generaliseringer, handler det om at finde et bestemt mønster eller en sammenhæng ud fra de specialtilfælde, man har. Herefter skal man indføre bogstavsymboler, som står for de ubekendte tal eller objekter, der indgår i mønsteret eller sammenhængen. Ved hjælp af disse kan man opstille et udtryk, der gengiver relationen mellem de ubekendte på generel form. Et eksempel er mønsteret med tændstikker, der ses herunder.
Figuren viser tre tændstikfigurer, der indgår i et mønster, hvor man fra én figur til den næste tilføjer to tændstikker, så der dannes en ny trekant.
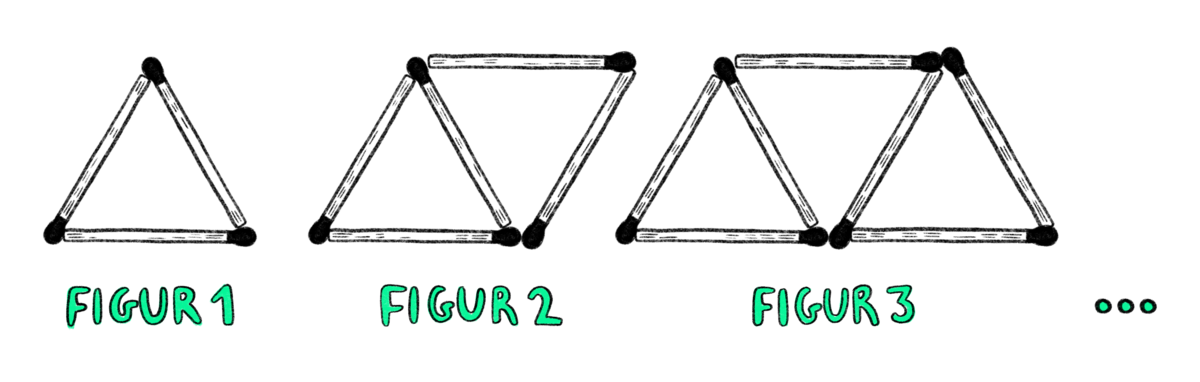
Ved hjælp af algebra kan man udtrykke, hvor mange tændstikker der skal til for at lave en vilkårlig tændstikfigur i mønsteret.
I dette eksempel har man:
• $3$ tændstikker i figur 1
• $3 + 2 = 5$ tændstikker i figur 2
• $5 + 2 = 7$ i figur 3Helt generelt kan man bestemme antallet af tændstikker i figur $n$, hvor $n$ er et naturligt tal, som:
$2\cdot (n-1) + 3$ tændstikker
Vi vælger her at skrive udtrykket på denne måde, så man tydeligt kan se, at man begynder med 3 tændstikker.
2. At beskrive sammenhænge
Verden omkring os er fuld af talsammenhænge, der kan beskrives vha. ord, figurer, tabeller og formler. Vi benytter algebra, når vi opstiller en formel, der kan beskrive sådan en sammenhæng.
Man kan for eksempel se på sammenhængen mellem, hvor meget det koster at køre på et lejet el-løbehjul, når man ved, hvad det koster at leje det pr. minut. Måske er der et startgebyr som i nedenstående tilfælde.

Eksempel: Beskrivelse af beregning af leje af løbehjul fra mobilsiden.dk (Kilde 2)
"Når du har fundet hen til dit udvalgte løbehjul, skal du låse det op, og herefter skal du connectes med løbehjulet. Så snart at du er "paired", starter din tur.
Hos selskabet er der lige nu en startpris på 10,5 kr.
Herefter betaler du per minut, du bruger løbehjulet. Prisen kan variere fra 1-3 kr i minuttet, alt efter udbud og efterspørgel.
Jeg har dog på min testtur betalt 1,5 kr per minut."
Ud fra oplysningerne i teksten kan man opstille en formel, der fortæller, hvor meget det koster at leje et el løbehjul i $m$ minutter, hvis minutprisen er den samme som på testturen.
Når først formlen er opstillet, kan den bruges til at løse konkrete problemer. Fx kan man bestemme, hvor meget det koster at leje et el-løbehjul i 14 minutter hos selskabet. Eller man kan sammenligne med et andet selskab, hvor der ikke er startgebyr, men hvor prisen pr. minut til gengæld er højere, fx 1,75 kr. Så algebraen hjælper os med at besvare spørgsmålet om, hvornår man skal vælge det ene selskab frem for det andet, hvis man vil betale så lidt som muligt.
3. Ved bevisførelse
Vi benytter ofte algebra til at bevise matematiske påstande og sætninger. Det gælder fx, at:
For ethvert tocifret tal, der ender på 5, vil kvadratet på tallet ende på 25.
Foran 25 står produktet af første ciffer og det tal, der er 1 større.
Med denne regel får vi at $35^2$ bliver $3 \cdot 4 = 12$ efterfulgt af 25, dvs. 1225, og $95^2$ bliver $9 \cdot10 = 90$ efterfulgt af 25, altså 9025.
Med algebra kan man gennemskue, HVORFOR det er sådan. Det ser vi nærmere på nu.
Da reglen handler om tocifrede tal, der ender på 5, så kan tallet skrives som n·10+5, hvor n er antallet af 10’ere i tallet. Fx kan 45 skrives som $4 \cdot10+5$, da der er 4 tiere. For at få alle de relevante tocifrede tal med skal $n$ antage værdierne $n = 1, 2, 3, …,9$.
Tager vi kvadratet på tallet, får vi:
$(n \cdot 10+5) \cdot (n \cdot 10+5) = 10 \cdot 10 \cdot n \cdot n + 2 \cdot 5 \cdot 10 \cdot n + 25 = 100 \cdot n \cdot (n + 1) + 25$.
Man kan nu se, at kvadratet er summen af de to tal: $100 \cdot n \cdot (n + 1)$ og 25.
Det sidste tal er 25, præcis som reglen siger, dvs. at vi har 2 tiere og 5 ettere.
Vi mangler derfor kun at fortolke det første tal. Hvis vi lige bytter om på rækkefølgen, står der $n \cdot (n + 1) \cdot 100$, og så er det nemmere at se, at dette tal angiver antallet af 100’ere, og dem er der $n \cdot (n+1)$ af. Antallet af 100’er er altså netop produktet af $n$ og det tal, der kommer efter $n$. (Kilde 1)
Ikke blot kan algebraen vise os, hvorfor en påstand gælder, men samtidig kan den give os indsigt i de metoder, man benytter til forskellige beregninger
4. At beregne og omforme
Talmysterier kan pirre elevers nysgerrighed: Hvordan kan det være, at læreren ved, hvad svaret er, når man selv vælger sit begyndelsestal?
Et talmysterium kan være:
- Tænk på et tal (og skriv det ned).
- Læg 2 til dit tal.
- Gang resultatet med 2.
- Træk 4 fra det, du fik.
- Dividér resultatet med det tal, du tænkte på.
- Nu har du tallet 2.
Herunder kan man se, hvordan dette simple talmysterium involverer både beregninger og omformninger. Efter at have prøvet med forskellige begyndelsesværdier, kan eleverne argumentere for, hvorfor de algebraiske formuleringer herunder viser, at man altid må komme frem til svaret 2. (Kilde 3)
| Trin | Instruks | Algebraisk formulering |
|---|---|---|
| 1. | Tænk på et tal (og skriv det ned) | $a$ |
| 2. | Læg 2 til dit tal | $a + 2$ |
| 3. | Gang resultatet med 2 | $(a + 2) \cdot 2 = 2a + 4$ |
| 4. | Træk 4 fra det du fik | $2a + 4 – 4 = 2a$ |
| 5. | Dividér resultatet med det tal, du tænkte på | $2a/a = 2$ |
| 6. | Nu har du tallet 2 | ☺️ |
Talmysteriet herunder stiller lidt større krav til behandlingen af de symbolske udtryk, der dukker op undervejs.
| Trin | Instruks | Algebraisk formulering |
|---|---|---|
| 1. | Tænk på et tal (og skriv det ned) | $a$ |
| 2. | Gang tallet med 2 | $2 \cdot a$ |
| 3. | Gang resultatet med det tal du tænkte på | $2 \cdot a \cdot a =2a^2$ |
| 4. | Gang det nye resultat med 4 | $2 \cdot a^2 \cdot 4 = 8 \cdot a^2$ |
| 5. | Træk 2 gange dit oprindelig tal fra | $8a^2 - 2 \cdot a$ |
| 6. | Dividér med dit oprindelige tal | $(8a^2 - 2 \cdot a)/ a = 8 \cdot a - 2$ |
| 7. | Læg 2 til | $8 \cdot a - 2 + 2 = 8 \cdot a$ |
| 8. | Dividér det du får med dit oprindelige tal | $8 \cdot a/a = 8$ |
| 9. | Nu har du 8 | ☺️ |
Man kan selv konstruere talmysterier, der lader eleverne arbejde med de typer omformninger eller regneregler, man ønsker. Eleverne kan selv lave den tilhørende algebraiske formulering, og man kan også lade eleverne selv formulere deres egne talmysterier.
Handlinger i algebra
Mens man i aritmetik udfører beregninger med tal, indgår der altså i algebra også bogstavsymboler, der kan stå for mange forskellige tal.
Læs også: Hvorfor er algebra så svært?
For at støtte elevers tilegnelse af algebraens mange elementer må man i undervisningen arbejde med mange forskellige former for algebraiske handlinger. (Kilde 1)
Man kan fx lave undervisningsaktiviteter, hvor eleverne skal:
- Bemærke, beskrive, benævne og repræsentere ift. en given kontekst
- Udtrykke og opstille symbolske udtryk
- Behandle symbolske udtryk
- Læse og fortolke symbolske udtryk
- Forbinde forskellige repræsentationer af samme fænomen.
Ofte vil aktiviteterne kombinere de nævnte handlinger, hvis aktiviteten skal være meningsfuld for eleverne. Herunder kan du finde eksempler på mindre aktiviteter, der illustrerer, hvordan eleverne kan arbejde med forskellige elementer af algebra.
1. Bemærke, beskrive, benævne og repræsentere
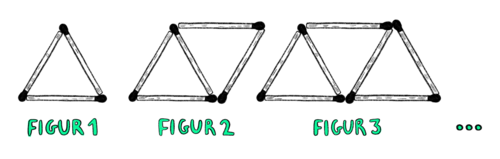
Man kan arbejde med tændstikmønsteret fra generaliseringseksemplet ovenfor og bede eleverne udtrykke antallet af tændstikker i en vilkårlig figur. De bemærker måske først, at hver gang man går fra en figur til den næste, bliver der lagt to tændstikker ekstra til, og at der derved dannes en ny trekant.
Mønsteret kan altså beskrives ved, at der i første figur er 1 trekant, i den næste 2 trekanter, derefter 3 trekanter osv.
Hvis den første figur kaldes figur 1, den næste figur 2, så figur 3, 4 osv., kan man helt generelt kalde den $n$’te figur for "figur $n$", hvor $n$ er et naturligt tal 1, 2, 3, 4 osv. Herefter kan antallet af tændstikker i den $n$’te figur benævnes med $y_n$, og sammenhængen mellem figurnummer og antal tændstikker kan repræsenteres i en tabel:
| Figurnummer | Antal tændstikker |
|---|---|
| $n$ | $y_n$ |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| - | - |
| - | - |
2. Udtrykke og opstille symbolske udtryk

I eksemplet "Bemærke, beskrive, benævne og repræsentere" har eleverne arbejdet med et tændstikmønster.
Efter indførelsen af de nødvendige symboler, kan eleverne udtrykke, hvordan antallet af tændstikker, udvikler sig i figurfølgen.
I den første figur er der 3 tændstikker, i den næste 5 og dernæst 7 tændstikker. Da man tilføjer 2 ekstra tændstikker, til den næste figur i rækken, bliver det til 9, 11, 13 osv. tændstikker.
Dernæst kan eleverne opstille et symbolsk udtryk, der fortæller, hvordan man finder antal tændstikker i den næste figur, $y_{n+1} = y_n+2$. I hvert trin har man altså brug for at kende det antal, man havde i det foregående trin, for at kunne finde det antal, man får.
Denne metode kaldes rekursion, og det udtryk, man kommer frem til, kaldes et rekursivt udtryk. I dette tilfælde fortæller det, at der i hvert trin skal tilføjes to tændstikker til den forrige figur for at få den næste, som vist i tabellen herunder.
| Figurnummer | Antal tændstikker | Forskel |
|---|---|---|
| $n$ | $y_n$ | $y_{n+1}$ - $y_n$ |
| 1 | 3 | |
| 2 | ||
| 2 | 5 | |
| 2 | ||
| 3 | 7 | |
| 2 | ||
| 4 | 9 | |
| 2 |
Måske kan eleverne også argumentere for, at når antallet af tændstikker i hvert trin vokser med 2, så vil antallet i den $n$’te figur kunne udtrykkes som en lineær funktion: $f(n) = 2 \cdot n +1$.
3. Behandle symbolske udtryk
At behandle symbolske udtryk kan involvere mange ting. Her viser vi et eksempel på, at algebraen kan hjælpe med at løse et problem ved at omskrive et udtryk og benytte substitutionsmetoden.
De fleste elever i udskolingen og i gymnasiet kender løsningsformlen for en generel andengradsligning: $a \cdot x^2 + b \cdot x + c = 0$.
Men hvad gør man, hvis man skal løse en fjerdegradsligning: $a \cdot x^4 + b \cdot x^3 + c \cdot x^2 + d \cdot x + e = 0$?
Det er komplekst at løse en generel fjerdegradsligning, men i de tilfælde, hvor det tilhørende 4. gradspolynomium er symmetrisk om en lodret akse (ligesom andengradspolynomiet jo altid er), er det noget nemmere.
Vi ser på den særlig simple udgave, hvor alle koefficienterne til de ulige potenser af $x$ er $0$. I dette tilfælde kommer fjerdegradsligningen (med nye symboler) til at se sådan ud: $a \cdot x^4 + b \cdot x^2 + c = 0$.
Med algebra kan vi indføre en ny variabel, $t$, som har den egenskab, at $t = x^2$. Man lægger mærke til, at $t$ må være et positivt tal. Først omskriver vi fjerdegradsligningen, så den kommer til at se ud som: $a \cdot (x^2)^2 + b \cdot x^2 + c = 0$. Dernæst substituerer (erstatter) vi med t, de steder, hvor der står $x^2$ og får: $a \cdot t^2 + b \cdot t + c = 0$. Nu har vi pludselig en helt almindelig andengradsligning, hvor vi kan finde løsningen for $t$ med den kendte løsningsformel. For at finde $x$, skal vi tage kvadratroden af $t$, da $t = x^2$, så $x =$ +/- $\sqrt{t}$.
4. Læse og fortolke symbolske udtryk

Når elever bliver bedt om at bestemme, hvor mange tern, der
er i den grå kant af et generelt $n$×$n$ gitter, som vist på billedet til højre, kan der fremkomme flere mulige udtryk, fordi eleverne har 'talt' ternene på forskellige måder.
Man kan også give eleverne nedenstående tre udtryk:
$2n + 2(n – 2)$
$4(n – 1)$
$4(n – 2) + 4$
Nu skal eleverne så fortolke og forklare, hvordan de hver især udtrykker relationen mellem kvadratets sidelængde og antallet af tern i den grå kant. (Kilde 1)
Man kan også opnå indsigter om forhold uden for matematikken ved at læse og fortolke algebraiske udtryk. Tænk bare på Ohms lov fra fysikken, der siger, at spændingsforskellen i et kredsløb $U$ er lig med produktet af modstanden $R$ og strømstyrken $I$. Eller udtrykt med symboler: $U = R·I$. Herfra kan man se, at spændingen vokser lineært (proportionalt) med både modstand og strømstyrke, og man kan se, at for fastholdt spænding vil en øget modstand give en mindre strømstyrke, en såkaldt omvendt proportionalitet.
5. Forbinde forskellige repræsentationer af samme fænomen
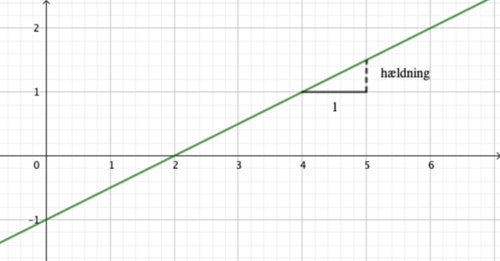
Når man forbinder forskellige repræsentationer, kan man udforske idéer, egenskaber og begreber ved et matematisk fænomen. Her ser vi på den vigtige egenskab 'hældning' ved lineære funktioner, som angiver funktionens konstante ændring pr. enhed.
De fleste elever i udskolingen kan fortælle, at en lineær funktion har forskriften
$f(x) = a·x + b$,
hvor $a$ er hældningen, og $b$ er skæringen med y-aksen. De ved også, at grafens hældning udtrykker dens stejlhed, dvs. "hvor meget man skal gå op (eller ned), når man går 1 hen?"
I en tabel kan hældningen ses som forskellen i $y$-værdierne, når forskellen i $x$-værdierne er 1.
Med algebra kan disse forskellige forståelser bringes sammen.
For hvorfor er $a$ det samme som grafens stejlhed? Hvorfor vil hældningen være forskellen på to $y$-værdier, som kommer efter hinanden i tabellen? Og hvad er sammenhængen mellem $a$ og brøken forskellen i $y$ delt med forskellen i $x$? Man kan stille mange flere undrende spørgsmål, og besvare dem med algebra!
Ser man på den særlige funktion $f(x) = a·x + a$ kan man spørge, hvad graferne for denne funktion for forskellige værdier af $a$ har tilfælles? En omskrivning af forskriften viser, at $f(x) = a·(x+1)$, dvs. uanset a’s værdi, så vil $f(-1) = 0$, og alle graferne går gennem punktet $(-1, 0)$.
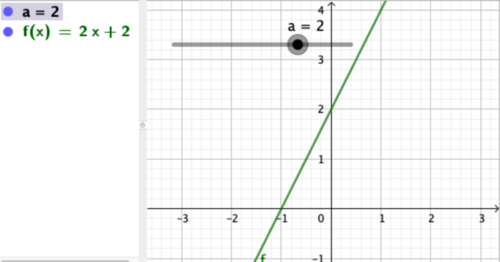
Dette kan også undersøges grafisk med en skyder. Lige meget hvilken værdi af a man vælger, vil grafen altid gå igennem $(-1, 0)$.

Ved at argumentere grafisk, kan eleverne opdage, at omskrivningen har en betydning, der går ud over det rent tekniske: I forskriften $f(x) = a·x + a$ er det første $a$ hældningen, og det andet $a$ er skæringen med $y$-aksen. Så hvis man går 1 til venstre (når $a > 0$) fra skæringspunktet på $y$-aksen, skal man gå $a$ ned, og så må man ende på $x$-aksen. Alle grafer skærer derfor $x$-aksen i $-1$, dvs. går gennem punktet $(-1, 0)$.
TIL OVERVEJELSE I FAGGRUPPEN
- Diskutér, hvad I forstår ved 'algebra'. Er listen i dette afsnit udtømmende, eller mangler der noget? Lav gerne jeres egen liste og definition på hvad algebra omfatter.
- Underviser I med (dvs. algebra inddrages og tydeliggøres i andre emner) eller i algebra? Eller måske begge dele?!
- Hvornår underviser I hhv. i og med algebra, og hvorfor?
- Formulér forskellige løsninger til tændstikproblemet ovenfor. Lav selv nogle lignende mønstre, hvis løsninger kan formuleres på forskellige måder. Hvordan vil I støtte eleverne til at indse, at de forskellige løsninger giver samme resultat?
til: GRUNDSKOLE & GYMNASIE
emne: ALGEBRA
UDGIVET: 2021
Forfatter
Marit Hvalsøe Schou
Gymnasielærer, ph.d.
Odense Tekniske Gymnasium
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Arcavi, A., Drijvers, P., & Stacey, K. (2016). The learning and teaching of algebra: Ideas, insights and activities. By:Routledge.
- Så let lejer du et el-løbehjul i København og Aarhus. mobilsiden.dk Lokaliseret d. 7.12.21 på: https://mobilsiden.dk/nyheder/mobilabonnement-telefoni/saa-let-lejer-du-et-el-loebehjul-i-koebenhavn-og-aarhus/
- Henriksen, A. (2016). Pattern Analysis as Entrance to Algebraic Proof Situations at C-level. Master thesis. INDs studenterserie nr. 48. https://www.ind.ku.dk/publikationer/studenterserien/
Yderligere materialer
- Jessen, B. E., Holm, C., & Winsløw, C. (2017) MatematikBroen – Fra grundskole til Gymnasium. IND’s skriftserie nr. 49. https://www.ind.ku.dk/publikationer/inds_skriftserie/nr.-492017-matematikbroen/Matbro_rapport_idunn.pdf
- Poulsen, C. S. (2015). Basic algebra in the transition from lower secondary school to high school. Master thesis. INDs studenterserie nr. 44. https://www.ind.ku.dk/publikationer/studenterserien/