Aktivitet og forløb: Kvadrat-sætningerne
Dette forløb handler om de tre klassiske identiteter, vi kalder kvadratsætningerne. De fleste elever har i grundskolen set arealmodeller for kvadratsætningerne. Ved at kombinere den geometriske tilgang med indførelse af algebra, får eleverne mulighed for at generalisere de resultater, de kender, og ræsonnere sig frem til nye sammenhænge. Forløbet er primært tiltænkt gymnasiet, men nogle aktiviteter kan anvendes i udskolingen, evt. som afslutning på lignende undersøgelser med tal, hvor eleverne efter at have eksperimenteret med tal og beregninger får mulighed for at udlede de generelle identiteter.
Undervisningsaktiviteterne viser en alternativ måde at indføre og vise kvadratsætningerne på (i særlig grad i gymnasiet). Her arbejder man videre med kendte billeder og modeller i stedet for at indføre symbolske udtryk, der ofte ikke giver mening for eleverne.
I gymnasiet benytter man ofte kvadratsætningerne og lignende omskrivninger ved bevisførelse. De er derfor en del af den algebraiske værktøjskasse, man præsenterer nye gymnasielever for (sammen med fx potensregneregler og manipulation af bogstavudtryk).
Kombination af algebraisk og geometrisk tilgang
Aktiviteter som dem, der præsenteres her, har imidlertid et større potentiale end at lære eleverne de tre klassiske kvadratsætninger. Når man kombinerer den algebraiske og den geometriske tilgang, får eleverne mulighed for at opleve, at de ligheder, som de ofte vil have mødt konkrete eksempler på tidligere, ikke blot er 'magi med bogstaver'. Eleverne får indblik i, at kvadratsætningerne ikke skal læses i en bestemt retning, de kan både læses fra venstre mod højre og omvendt. Det gør man ved at anskueliggøre, at symbolerne har en betydning, der går ud over at udføre grundlæggende beregninger som fx at gange ind i en parentes. Symbolerne kan give mening, når man ser på dem som en repræsentation af nogle arealer. De er ligheder eller identiteter.
Forløbet viser, hvordan man kan arbejde med kvadratsætningerne ved at inddrage både en geometrisk og en symbolsk repræsentationsform. Aktiviteterne er udviklet på Freudenthal Instituttet i Holland, der er et stærkt fagdidaktisk miljø. De kan udvides efter behov, og man kan vælge at bruge flere af dem i et samlet forløb eller inddrage dem enkeltvis i løbet af andre undervisningsforløb.
Aktiviteterne trækker på flere af de elementer som skolealgebraen indeholder nemlig at udtrykke generaliseringer, at beskrive og opstille sammenhænge og at udføre beregninger og omformninger.
Læs også Hvad er skolealgebra?
Mange elever har nok allerede i grundskolen mødt flere af aktiviteterne i en udgave, hvor der er benyttet konkrete tal frem for generelle symboler. Afhængigt af elevernes behov kan man lade klassen eller enkelte grupper af elever starte aktiviteterne på denne konkrete måde. Det kan også være en god idé at lade eleverne selv tegne figurer (eller udlevere kopiark med figurerne) og klippe og flytte rundt med brikkerne, så de beskrevne ligheder bliver tydelige. Nogle af aktiviteterne er illustreret med et GeoGebra-dokument, hvor eleverne selv kan vælge værdier for a og b, og som viser, at sætningerne gælder uafhængigt af dette valg.
Forløb
- Iscenesættelse: Eleverne får at vide, at de nu skal bevise nogle ligheder, der kaldes for kvadratsætningerne, fordi nogle af leddene er sat i anden. Man kan både vise dem ved at regne og ved at bruge figurer, og her skal begge metoder benyttes.
- Elevernes selvstændige arbejde: Eleverne arbejder sammen i grupper. Man kan fx vælge at udlevere hver aktivitet som et arbejdsark, som de får en afgrænset tid til at arbejde med.
- Fælles samtale: Mellem hver aktivitet gør eleverne rede for, hvordan de har arbejdet med problemstillingerne, og hvad de har svaret på spørgsmålene i en fælles klassesamtale. Lærerens rolle er at få eleverne til at argumentere, og at gøre det tydeligt, hvilke argumenter der er nødvendige og hvorfor. Desuden skal der i samtalen være fokus på hvordan denne type argumenter formuleres, og de generelle resultater skal trækkes frem.
- Læringsudbytte: Gennem arbejdet med aktiviteterne i dette forløb får eleverne mulighed for at opleve, at der er sammenhæng mellem konkrete talberegninger og symbolske udtryk, og at symbolerne kan stå for mange forskellige tal. Eleverne oplever styrken af et algebraisk argument, og de bliver selv i stand til at benytte og formulere sådanne algebraiske argumenter i en kontekst, hvor det hele tiden er muligt at illustrere omformningerne i en anden repræsentationsform.
Mange elever har problemer med variabelbegrebet i algebra, hvor de indgående symboler kan antage mange forskellige værdier. Det gælder også i kvadratsætningerne. Her kan man lade eleverne eksperimentere med et GeoGebra-dokument som dette, hvor eleverne vha. skydere tydeligt kan forvisse sig om, at betydningen af symbolerne i 1. kvadratsætning er uafhængige af deres størrelse.
Aktivitet 1 – Første kvadratsætning
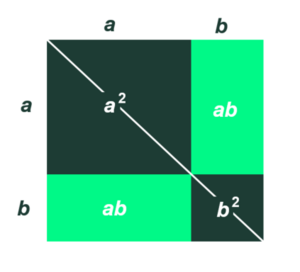
Den 1. kvadratsætning handler om kvadratet på en sum af to reelle tal: $(a + b)^2 = a^2 + b^2 + 2 \cdot a \cdot b$. Sætningen kan også tolkes som arealet af et kvadrat med sidelængden a + b som vist på figuren.
Eksempler på spørgsmål:
- Forklar ud fra figuren hvorfor $(a +b)^2$ er det samme som $a^2 + b^2 + 2 \cdot a \cdot b$.
- Kan du også ud fra figuren argumentere for at $a^2 + b^2 + 2 \cdot a \cdot b = (a + b)^2$?
En pointe eleverne gerne skulle frem til er, at sætningen er en identitet. Det er altså ligegyldigt hvilken vej, man læser ligheden.
1. kvadratsætning kan bruges til hurtigt at beregne visse regnestykker. Sætningen giver fx, at $11^2 = (10 + 1)^2 = 10^2 + 1^2 + 2 \cdot 10 \cdot 1$, hvor det sidste udtryk er nemt at udregne: $100 + 1 + 20 = 121$. Følgende opgaver kan man stille eleverne:
- Beregn følgende regnestykke uden lommeregner: $37^2 + 63^2 + 2 \cdot 37 \cdot 63$
- Antag at $b = a$. Vis, at $(a + a)^2 = a^2 + a^2 + 2 \cdot a \cdot a$, og at det er det samme som, at $4a^2 = 4a^2$, som jo helt tydeligt er sandt!
- Passer dette med den grafiske fortolkning?
- Antag, at $b = 2 \cdot a$, og tjek, at kvadratsætningen gælder.
I den efterfølgende fælles samtale i klassen, kan læreren spørge til, hvorfor det er relevant at beskæftige sig med en kvadratsætning som denne?
Aktivitet 2 – Kvadratet af en sum af tre reelle tal
I den sædvanlige udgave af 1. kvadratsætning lægger man to reelle tal sammen.
Men hvad sker der, hvis man lægger tre reelle tal sammen? Eller 4 tal? Eller …
Her kan man igen drage nytte af kombinationen af algebra og en grafisk fremstilling.
Eksempler på spørgsmål:
(Brug figuren nedenfor, eller lad eleverne tegne den selv til at forklare, hvorfor følgende lighed gælder):
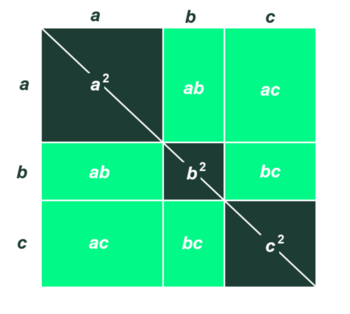
- $(a +b + c)^2 = a^2 + b^2 + c^2 + 2 \cdot a \cdot b + 2 \cdot a \cdot c + 2 \cdot b \cdot c$
- Lad $c = 0$ på begge sider. Hvilken formel får man så?
- Antag, at $a = b = c$. Man kan nu skrive begge sider, ved hjælp af et enkelt bogstav. Tjek ved beregning, at de to sider er ens.
- Kvadratet af $111$ har et sjovt resultat: $12321$. Prøv at skrive $111$, som en sum af tre tal, der gør det muligt for dig, nemt at tjekke resultatet! (Hint: $100$, $10$ og $1$).
- Brug figurer som ovenstående til at finde tilsvarende ligheder, når man tager kvadratet på summen af 4 eller 5 tal. Tjek resultatet ved beregning.
- Undersøg, om $1111^2 = 1234321$ og $11111^2 = 123454321$.
Argumentér for din påstand ved hjælp af algebra.
Aktivitet 3 – Kvadratet på differensen mellem to reelle tal
Den anden kvadratsætning lyder: $(a - b)^2 = a^2 + b^2 - 2 \cdot a \cdot b$
- Lav en figur, der svarer til den, du brugte i 1. kvadratsætning, som kan bruges til at argumentere for 2. kvadratsætning. Alternativt kan man give eleverne figuren nedenfor og lade dem forklare ligheden ud fra billedet.
- Er formlen rigtig, når $a = b$? Forklar.
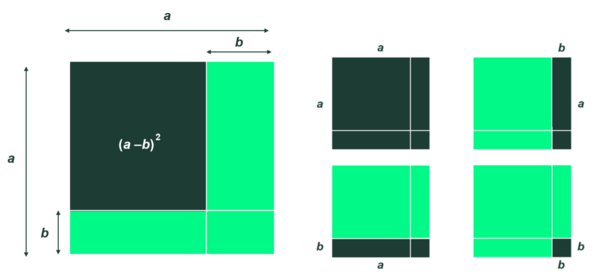
Aktivitet 4 – At kombinere 1. og 2. kvadratsætning
- Forklar formlen nederst på billedet ud fra figuren.
- Tjek ud fra de to ligheder, at resultatet passer.
- Beregn uden brug af lommeregner: $99^2 + 101^2$ og $49^2 + 50^2 + 51^2$
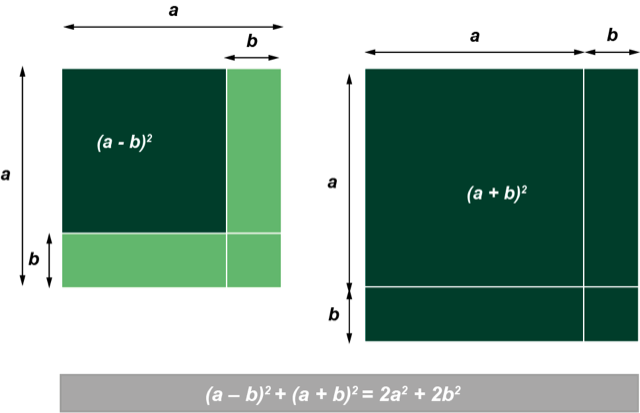
Vi kan også trække de to udtryk fra hinanden:
- Forklar formlen nederst på billedet ud fra figuren, og eftervis den ved beregning
- Tjek, at formlen gælder, når $a = b$.

Aktivitet 5 – To tals sum gange deres differens
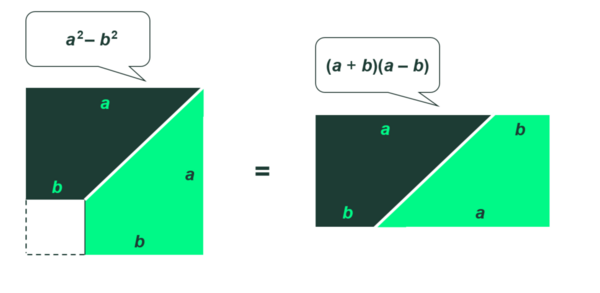
Den tredje og sidste kvadratsætning hedder $(a + b) \cdot (a – b) = a^2 – b^2$
- Forklar, hvad figuren viser, og benyt den til at argumentere for rigtigheden af den 3. kvadratsætning.
- Tjek ligheden ved beregning.
Man kan benytte 3. kvadratsætning til at beregne $54^2 – 46^2 = (54 + 46) \cdot (54 – 46) = 100 \cdot 8 = 800$
- Beregn på samme måde og uden lommeregner:
$52^2 – 48^2 =$ ___________________
$67^2 – 33^2 =$ ___________________
$501^2 – 499^2 =$ _________________
Lav selv nogle lignende stykker.
Mads mener, at $100$ – $k$ ganget med $100 + k$ må være lig med $100^2$, for $100$ – $k$ er jo $k$ mindre end $100$, og $100 + k$ er $k$ større, så de to må gå ud med hinanden.
- Benyt algebra til at argumentere for, at Mads ikke har ret. $100^2$ er større end produktet af $100$ – $k$ og $100 + k$. Hvor meget større?
- Undersøg også, hvor meget $ n^2$ er større end produktet af $n + 10$ og $n$ – $10$.
TIL OVERVEJELSE I FAGGRUPPEN
- Planlæg i samarbejde et kort forløb, hvor ovenstående aktiviteter indgår. I hvilken sammenhæng (fx hvilket matematisk indhold?) vil forløbet passe ind?
- Hvor nogle elever har nemt ved at udføre symbolske manipulationer, kæmper andre med konkrete talberegninger. Hvordan kan man formulere aktiviteterne, så der bliver udfordringer for alle elever, og så alle elever opnår forståelse for algebra?
til: GRUNDSKOLE & GYMNASIE
emne: ALGEBRA
UDGIVET: 2021