Taltricks og design af undervisning
Som et led i at styrke elevernes algebraiske færdigheder, uden at de bliver kvalt i utallige træningsopgaver, kan opgavedesigns som taltricks inddrages i undervisningen. Taltricks er ikke kun gavnlige for at styrke allerede kendte algebraiske fænomener, men kan ligeledes designes til at udvikle nye algebraiske færdigheder og teknikker. Taltricks kan tilrettelægges til at behandle lige netop den udfordring eller teknik, man ønsker, samt kun optage den tid man har til rådighed i undervisningen (Kilde 1).
Hvad er et taltrick?
Et taltrick, som de har været implementeret i dansk grundskole og gymnasiekontekst, består af én A4-side, som er inddelt i overskrifterne Kommando, Tal og Bogstavsudtryk. Kolonnen med Kommando vil typisk være udfyldt af læreren med kommandoer, som eleverne følger med konkrete selvvalgte taleksempler i Tal-kolonnen. De konkrete taleksempler skal motivere og hjælpe eleven med først at opdage et mønster, der kan pirre en nysgerrighed ift. at opklare mysteriet eller afsløre tricket. Det skal gerne give motivation hos eleven at udtrykke kommandoerne generelt med bogstaver under Bogstavudtryk for at skabe overblik og afsløre pointen med tricket. Ofte vil eleverne have valgt forskellige konkrete tal, hvilket giver forskellige beregninger. Så når eleverne skal dele deres arbejde og dele gode idéer for at komme videre i opklaringen af mysteriet, skabes der yderligere behov for en generalisering, der naturligt vil tage form af bogstaver som pladsholdere.
Måden der i denne tekst arbejdes med taltricks trækker på Teorien om Didaktiske Situationer og dialektikken mellem elevers selvstændige arbejde, gruppearbejde og fællesgørelse af viden gennem validering og institutionalisering af elevernes arbejde. Ydermere er det en måde at arbejde undersøgende i faget og med faget, jf. Undersøgelsesbaseret Matematikundervisning på gymnasialt niveau.
Taltricks har til formål at imødekomme den arbejdsgang, som eleverne kender fra grundskolens matematikundervisning, som tager udgangspunkt i konkrete tal (Kilde 2), og taltricks kan med fordel inddrages for at lette overgangen mellem grundskolen og gymnasiet.
Eksempler på taltricks
Her præsenteres eksempler på tre taltricks. De kan indgå som en samlet undervisningssekvens, men kan også fint bruges enkeltvist. I nogle klasser har de været brugt som den daglige opvarmning, som eleverne helst ikke ville undvære.
De tre taltricks kan downloades her
Som det fremgår af eksemplerne, kan et taltrick ramme præcist de algebraiske regler og manipulationer, man ønsker, at eleverne skal arbejde med, konstruere viden om eller eksplicit italesætte. De kan altså varieres i det uendelige, hvor eleverne fortsat kan have en oplevelse af, at de laver noget nyt. Det er ikke den samme metode eller strategi i 10 lignende opgaver, der kan give eleverne en oplevelse af, at hvis man ikke kan den første, så kan man heller ikke resten. Der er med andre ord mulighed for en lav indgangstærskel (alle kan følge kommandoerne og regne med tallene), samtidig med at der sikres et højt abstraktionsniveau, hvor man ender med mere eller mindre teoretiske begrundelser.
Opgave 1 – Den distributive lov og brøker

De tre taltricks er opbygget således, at opgave 1 har til formål at introducere taltricks som opgavetype for eleven. Derfor er opgavens algebraiske indhold mindre kompliceret for at kunne imødekomme udfordringer med selve opgavens format. Bruges den i grundskolen, vil den kunne tjene det formål, at arbejde med den distributive lov og brøkregneregler. Bogstavudtrykket, der opbygges, bliver således:
$\frac{(a+5)\cdot 2 -2}{2}-4$
Eleverne ved fra taleksemplerne, at dette kan reduceres til det tal, de startede med at tænke på, $a$. Herefter kan de vælge flere strategier til reduktion: divider igennem med 2 (hvor man husker ikke at dividere ind i parentesen), eller man kan benytte den distributive lov først. At formulere de forskellige strategier og teknikker for hinanden vil styrke elevernes autonomi ift. algebra. Desuden vil lærerens orkestrering af valideringen – altså at sammenholde de forskellige tilgange, kunne styrke elevernes indsigt i regnereglernes generelle værdi, fordi reduktionen kan laves på forskellige måder med anvendelse af samme teknikker i forskellig rækkefølge, samt at nogle fremgangsmåder kan være smartere end andre
Så ikke nok med at introducere taltrick som opgavetype, så kan aktiviteter som denne også være en måde for eleverne at genopfriske grundskoleviden, uden at det bliver en endeløs række af træningsopgaver. Det kan give læreren et indblik i hvilke algebraiske teknikker eleverne er i stand til at aktivere og bruge autonomt uden en klassisk form for stilladsering. Dermed er denne type aktivitet velegnet til opstarten af grundforløbet.
Hvis man tænker de tre tricks som en sekvens, så har opgave 2 til formål at gøre eleven bekendt med første kvadratsætning, der skal benyttes i opgave 3. Alternativt kan opgave 2 bruges som en screening til, hvorvidt eleverne kan aktivere første kvadratsætning eller ligefrem lære den. Yderligere kan taltricks med fordel bruges som en trædesten til det mere teoretiske arbejde med differentialregningen, som allerede indikeret i 'Hvorfor algebra i gymnasiet?'. Her vil nedenstående taltrick være en relevant opvarmningsaktivitet, inden eleverne påbegynder bevisarbejdet vha. tretrinsreglen for at bevise, at hvis funktionen $f(x)=ax^2$, så er den afledte $f'(x)=2ax$. Eller måske endnu vigtigere, når eleverne skal bevise løsningsformlen for rødderne i andengradspolynomier, hvor de netop skal kunne genkende leddene, der fremkommer af kvadratet på en toleddet størrelse og trække dette sammen i en parentes.
Opgave 2 – Første kvadratsætning
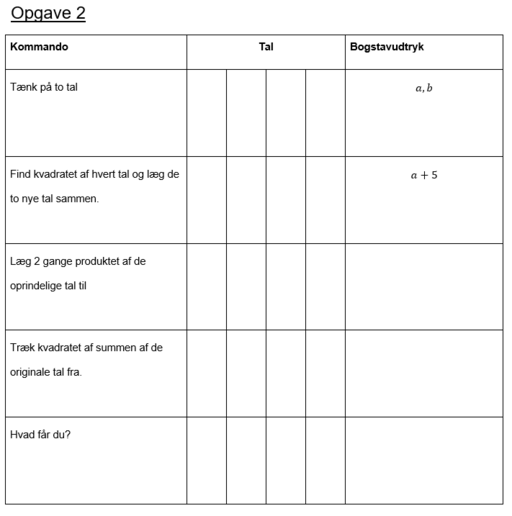
Skriver man i opgave 2 kommandoerne op med bogstavudtryk (og har valgt at tallene skal hedde a og b) får man:
$a^2+b^2+2ab-(a+b)^2$
Gennem taleksemplerne vil eleverne have opdaget, at dette altid giver $0$. Dvs. at opklaringen eller afsløringen af tricket handler om at finde et argument for, at
$a^2+b^2+2ab-(a+b)^2=0$
Her er der tale om et mere lukket trick, hvor der ikke er mange andre strategier end at udregne:
$(a+b)^2=(a+b)\cdot(a+b)=a\cdot(a+b)+b\cdot(a+b)=a\cdot a+a\cdot b+b\cdot a+b\cdot b$
Det sidste lighedstegn og brugen af den distributive lov vil helt sikkert volde nogle af eleverne problemer. Vi kan gætte eller håbe på, at de kan støttes af at kende det ønskede resultat. Omvendt vil dette afgjort være en anledning til at genbesøge, hvad den distributive lov siger. Endelig får eleverne brug for den kommutative lov for at se, at $a\cdot b=b\cdot a$, så $a\cdot b+b\cdot a=2ab$.
Hvis pointen med taltricket eller en række af dem er at lære første kvadratsætning, vil flere trick med flere mulige løsningsstrategier, der giver mulighed for sammenligninger som i den første, være et stærkere redskab.
Det skal bemærkes, at opgave 2 yderligere kan tænkes som en indføring i fagsproget på gymnasialt niveau. For hvad betyder det at ”finde kvadratet af hvert tal” eller ”læg to gange produktet til”? Det kan gøres til en selvstændig pointe, når eleverne er fortrolige med taltricks at udfordre dem sprogligt og lade dem undersøge, hvad disse vendinger kan betyde i matematik. Igen giver formatet et utal af variationsmuligheder, der kan understøtte elevernes læsning af lærebogen.
I den sidste opgave skal eleven sammensætte sin tilegnede viden om den distributive lov og første kvadratsætning i et længere algebraisk udtryk, som skal reduceres. Udgangspunktet er en tidligere eksamensopgave, der gav eleverne en del vanskeligheder, se 'Hvorfor algebra i gymnasiet'.
Opgave 3 – fra læringsvanskelighed til læringsmulighed
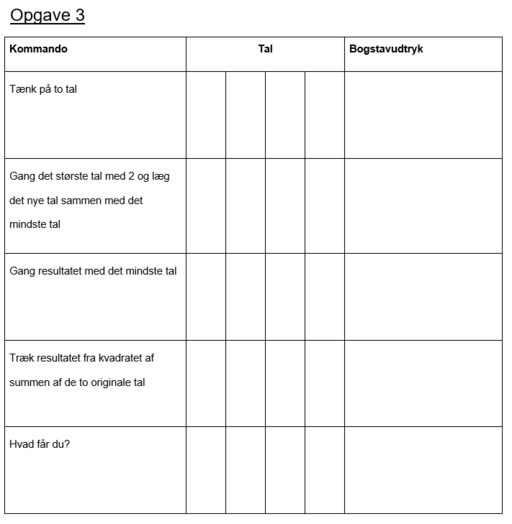
Udgangspunktet for dette taltrick er en reduktionsopgave, der gav eleverne store udfordringer til den skriftlige prøve uden hjælpemidler ved studentereksamen i 2019 på B-niveau.
Bogstavudtrykket, der skal reduceres i denne opgave, og svarer til den svære opgave ved B-niveau eksamen, er følgende:
$(a+b)^2-(2a+b)\cdot b$
I taltricksversionen her ved eleverne fra taleksemplerne, at svaret skal være $a^2$. Hypotesen er, at i denne form vil eleverne bruge den distributive lov og første kvadratsætning til at overkomme udfordringen med at reducere udtrykket – om ikke andet, så ved fælles hjælp og inspiration i valideringen af elevernes arbejde. Stilladseringen i taltricks betyder, at de anvendte regler og lovmæssigheder bliver til teknikker eleverne aktivt kan bruge i stedet for blot et navn eller en vending, de kender til.
Det er værd at bemærke, at en variation af taltricks kan øve den mundtlige dimension, ved at eleverne får de algebraiske udtryk og skal forklare dem i ord efter at have sat konkrete tal ind. Det giver særligt en mulighed for at arbejde med elevernes fagsprog og talte sprog – hvilke formuleringer er mest præcise?
Endelig kan man ind i mellem lade eleverne selv designe taltricks, prøve dem af på hinanden, og lade dem forklare, hvilken matematik der kommer i spil både i de andres og deres egne designs. Dette vil være med til at variere undervisningen og brugen af taltricks.
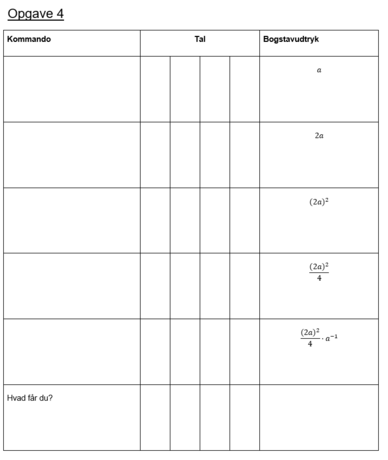
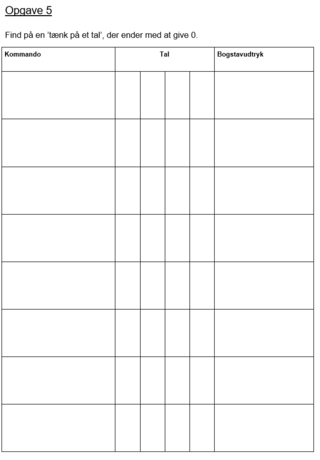
Taltricks i undervisningen
For at overskueliggøre arbejdet med taltricks i undervisningen indeholder denne boks en gennemgang af forløbene med
Teorien om Didaktiske Situationer
som ramme. Opgaverne er designet således, at alle fem faser skal gennemgås for én opgave før klassen samlet, kan gå videre til den næste. Forløbet af de enkelte opgaver vil dermed minde meget om hinanden, blot med forskellige udregninger og algebraiske udtryk, og dermed være forskellige aktioner og opfattes forskellige i elevernes optik.Opstart af undervisningen og dermed den første devolution vil bestå af at læreren læser kommandoerne højt og eleverne følger instruktionerne. Måske læreren har medbragt dem på slides og lader eleverne prøve at følge instruktionerne et par gange, så flest mulige får en aha oplevelse. Herefter spørger læreren hvad eleverne ser? Hvilket kan være at svaret altid er 0, 5 eller det tal de tænkte på, afhængigt af hvilket taltrick de arbejder med. Hvorefter læreren spørger, gælder det altid? Hvordan kan det være? Hermed har læreren overleveret problemet med at finde et mønster og forklare det. Samtidig er miljøet blevet overleveret som almindelige regneregler, anvendelse af heltal samt evt. generalisering med bogstaver. Eleverne har allerede påtaget sig, at forstå problemet og mønsteret, samt at kunne forklare det. Vi kalder denne fase for devolutionen. Herefter udleveres arbejdsarket, der kan støtte elevernes videre arbejde.
De fleste elever vil have set mønsteret, men har måske brug for at gentage beregningerne et par gange mere for at blive overbevist om, at der faktisk er et mønster. Nogle vil måske gå tilbage og rette tidligere (fejl)beregninger for mønsteret fremkommer for alle valgte starttal. Her vil arbejdsarket være en god stilladsering. Ikke mindst at oversætte instruktionerne til generelle udtryk ved brug af bogstaver. Det vil være forskelligt, hvor langt eleverne kommer med at reducere bogstavudtrykket. Her vil det for nogle være en hjælp at bruge taleksemplerne til at opdage eller indse brugen af fx den distributive lov. Vi kalder dette for handlingsfasen, hvor læreren lader eleverne arbejde uden hints eller indblanding. Derimod skal læreren observere de strategier og metoder eleverne trækker på og udvikler.
Når alle har haft tid til at arbejde sig ind på problemet, skal eleverne dele deres svar – helst gerne på skrift – ved at præsentere ved tavlen, mega post-its eller A3 ark hængt på væggene, eller fx en padlet, hvor elever skriver eller deler billeder af deres notepapir. Læreren organiserer herefter formuleringsfasen ved at bede elever eller elevgrupper præsentere deres arbejde fx ved at starte med konkrete taleksempler til at slutte med mere generelle og algebraisk velstrukturerede svar. Denne fase vil naturligt glide over valideringsfasen, hvor elevernes argumenter sammenholdes og evt. misforståelser rettes, og mere avancerede svar forstås gennem de konkrete eksempler giver. Jo mere eleverne kan deltage i dette arbejde, desto bedre – også gerne med opklarende spørgsmål. Endelig institutionaliserer læreren, hvordan instruktionerne kan oversættes til et algebraisk udtryk, samt hvordan dette reduceres til det forventede svar.
Læs mere i det tværgående tema om planlægning af undervisningen, hvordan undervisning designet med afsæt i Teorien om Didaktiske Situationer understøtter elevernes læring og deres mulighed for at konstruere viden selv.
Andre opgaver af samme natur
Det er værd at bemærke, at der findes en lang række andre opgaver, der er designet med samme intention om at lade eleverne arbejde undersøgende og udvikle deres evner til algebraisk manipulation samt lære algebraiske teknikker. For eksempel kan man læse mere om undersøgende opgaver omhandlende mønstre i udvalgte tabeller i Aske Henriksens speciale. De første opgaver handler om mønstergenkendelse og mere basal skolealgebra. Opgaverne kan udvides til at omhandle determinanten, som kan indgå i et forløb om vektorregning.



En anden opgavetype, som træner specifikke regneoperationer, kan findes i MERIA (Kilde 4). Her beder en hollandsk lærer sine elever udfylde det resterende af en halvfyldt pyramide, hvilket ligeledes træner mønstergenkendelse og regneteknik.
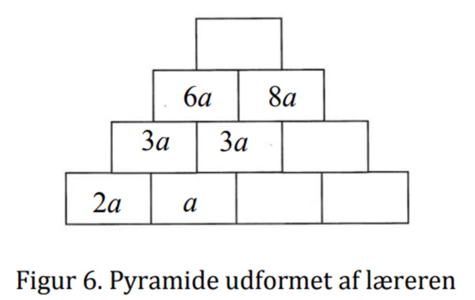
Alternativt kan man bede sine elever opstille deres egen pyramide med selvvalgte regneregler. Dette giver mulighed for at få et overblik over elevernes evne til selv at producere og konstruere algebraiske udtryk (Kilde 4, s. 28). Disse pyramider kan desuden bruges til at udfordre eleverne på tværs af klasserne ved at lade dem først designe og derefter løse hinandens pyramider med et på forhånd fastsat sæt af regneregler og lovmæssigheder.
til: GYMNASIER
emne: ALGEBRA I GYMNASIET
UDGIVET: 2023
Forfattere
Milla Mandrup Fogt
Stud.Scient
IND og MATH på KU
Britta Eyrich Jessen
Adjunkt
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Kilde 1: Jensen, A. B. (2015). Number tricks as a didactical tool for teaching elementary algebra (Specialerapport). Københavns Universitet, https://www.ind.ku.dk/publikationer/studenterserien/studenterserien- alle/studenterserie41/Thesis.Asger.Brix.pdf.
- Kilde 2: Schou, M. H. (2018). Actors at the scene of mathematics (Ph.D.-afhandling). Laboratory for Coherent Education and Learning.
- Kilde 3: Henriksen, A. (2016). Pattern Analysis ad Entrance to Algebraic Proof Situations at C-level (Specialerapport). Københavns Universitet, https://www.ind.ku.dk/publikationer/studenterserien/studenterserien-alle/studenterserie48/ASKE_speciale_m._forside.pdf
- Kilde 4: Winslöw, C., Jessen B., Doorman M., Bos R. (2017). Meria håndbog i undersøgelsesbaseret matematikundervisning. Project MERIA, https://meria-project.math.hr/sites/default/files/2018-02/MERIA%20Practical%20Guide%20to%20IBMT_DEN.pdf