Tilgang – At subtrahere flercifrede tal
Læringssporet tager udgangspunkt i problemer fra elevernes hverdag, som kan løses med addition og/eller subtraktion. Man kalder dem også for additive situationer (se læringsspor ”At addere etcifrede tal” og tema ”At regne med etcifrede tal”). Der er fire sådanne situationer:
Læg til-situation:
Der er $17$ børn i svømmehallen. Efter en time er der $32$. Hvor mange børn kom i løbet af den time?
Træk fra-situation:
Der er $32$ børn i svømmehallen. Efter en halv time går $11$ af dem hjem. Hvor mange børn er tilbage i svømmehallen?
Del-helhed-situation:
Der er $32$ børn i svømmehallen. $17$ børn er i vandet, og resten sidder på kanten. Hvor mange børn sidder på kanten?
Sammenlign-situation:
Der er $32$ børn i svømmehallen. Der er $2$ børn flere i vandet end på kanten. Hvor mange børn er i vandet?
En additiv situation er et problem fra elevernes hverdag, der kræver brug af addition eller subtraktion (Carpenter et al., 1999).
Disse hverdagsproblemer kan løses med subtraktion, når helheden – her antal børn i svømmehallen – er kendt. For hver situation kan der stilles tre forskellige spørgsmål ved at lade to tal være kendte og det sidste tal være ukendt. I træk fra-situationen spørges til resultatet, men man kan også spørge til en ukendt ændring, fx ”Der var $32$ børn i svømmehallen, og nu er der $21$ børn tilbage. Hvor mange børn er gået hjem?” eller en ukendt startværdi, fx ”Nu er der $21$ børn i svømmehallen. $11$ børn er gået hjem. Hvor mange børn var der i svømmehallen til at starte med?”. Generelt bliver situationerne sværere at løse, når ændringen eller startværdien er ukendt (se Grundlag i læringsspor "At addere etcifrede tal" og tema "At regne med etcifrede tal" for flere detaljer). Det er en pointe, at addition og subtraktion er tæt knyttede, da de er hinandens modsatte regningsarter, og at de begge kan være i spil (mere eller mindre direkte), når elever subtraherer flercifrede tal.
De to vigtigste idéer i læringssporet er:
- De strategier til subtraktion af flercifrede tal, som en klasse i fællesskab kan udvikle.
- De repræsentationer, der kan støtte eleverne i at udvikle deres tænkning om subtraktion.
Udvikling af strategier til subtraktion
Læringssporet bygger videre på elevernes erfaringer med addition af naturlige tal og subtraktion af tallene op til $20$. For subtraktion af tal op til $20$ findes en progression i elevers udvikling af strategier, men det gør der ikke for subtraktion af flercifrede tal (se Grundlag). Når elever skal lære at subtrahere flercifrede tal, anbefaler forskning, at eleverne opbygger et bredt repertoire af strategier, hvorfra de kan vælge og tilpasse en (eller flere) strategier til en bestemt situation eller subtraktionsstykke. Anbefalingen er altså, at eleverne lærer at subtrahere fleksibelt. Et for ensidigt fokus på bestemte strategier eller en for tidlig introduktion af cifferbaserede strategier kan gøre det vanskeligt for eleverne at forstå de matematiske begreber, der indgår, og at udvikle fleksibilitet i deres strategibrug. Eleverne vil være tilbøjelige til at benytte den introducerede strategi eller algoritme.
I læringssporet er der fokus på tre overordnede strategier til subtraktion af flercifrede tal:
- Sekventielle strategier (eller hoppe-strategier): Her bruger eleverne tallene på en tallinje og subtraherer ved at bevæge sig – eller hoppe – langs tallinjen enten fremad (addition) eller bagud (subtraktion).
- Opdelingsstrategier: Her bruger eleverne deres kendskab til positionssystemet og subtraherer ved at dele op og samle i enere, tiere, hundrede osv.
- Kompensationsstrategier: Her laver eleverne situationen eller stykket om til et, de kender, regner det og retter det derefter til, så det passer til den oprindelige situation eller stykke.
Til hver af de tre strategier kan eleverne tænke om subtraktion på tre forskellige måder, der ligger i forlængelse af deres tidligere erfaringer med at addere og subtrahere tal op til $20$ (se Grundlag):
- Direkte subtraktion, der ligger i forlængelse af elevernes første erfaringer med at tage væk med støtte i konkrete materialer.
- Indirekte addition (eller fyld op), der ligger i forlængelse af at tænke op til 10.
- Indirekte subtraktion, der ligger i forlængelse af at tænke ned til 10.
I skemaet er de tre strategier og de tre tænkemåder eksemplificeret ud fra $47-16$. Det er ikke meningen, at klassen nødvendigvis skal lære alle 9 kombinationer, fx er det ikke intuitivt at tænke opdeling, som indirekte addition eller indirekte subtraktion.

I cifferbaserede strategier deler man fx 83 op i 8 og 3 uden at tænke på, at 8 repræsenterer antal tiere. I talbaserede strategier ser man derimod på den værdi cifrene repræsenterer, fx ses 8 i 83 som 80. (Hickendorff et al., 2019, s. 544).
I læringssporets første tre faser er fokus på at støtte en klasse i at udvikle de tre strategier og tænkemåder. Det er en fordel, hvis klassen lærer navnene på de tre strategier, men ikke nødvendigvis på tænkemåderne. Strategierne (og tænkemåderne) kan eventuelt kaldes noget andet fx hoppe-strategier, dele op-strategier og lav om og ret til-strategier i stedet for sekventielle, opdelings- og kompensationsstrategier. Hvis klassen kan subtrahere fleksibelt sidst i læringssporet, kan læreren overveje at introducere en såkaldt kolonne-metode, der kan indgå i klassens repertoire af strategier.
Kolonne-metoden er en talbaseret metode ligesom de strategier, klassen hidtil har arbejdet med i læringssporet, men den skrives typisk op lodret på samme måde som cifferbaserede strategier. Når man regner fx $87 - 35$ med kolonne-metoden, skriver man tallene lodret som i Figur 2 og regner fra venstre mod højre. Det vil sige, at man subtraherer $30$ fra $80$ og $5$ fra $7$. Det giver $50$ og $2$, altså $52$. I fase 4 (se fase 4 i Praksis) vises, hvordan metoden kan bruges ved tierovergang.
Cifferbaserede strategier til subtraktion indgår ikke i læringssporet.
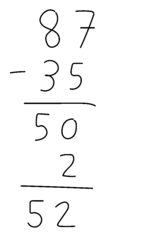
Udvikling i brug af repræsentationer
Det er hensigten, at eleverne gradvist udvikler deres måder at repræsentere deres strategier og tænkning om subtraktion. Særligt to repræsentationer er vigtige. Den første, den åbne tallinje, er god at bruge, når en klasse skal udvikle sekventielle strategier, mens den anden, veksle-pladen, er god til at støtte deres udvikling af opdelingsstrategier. I læringssporets første to faser er klassens udvikling af sekventielle strategier derfor adskilt fra deres udvikling af opdelingsstrategier.
Den åbne tallinje
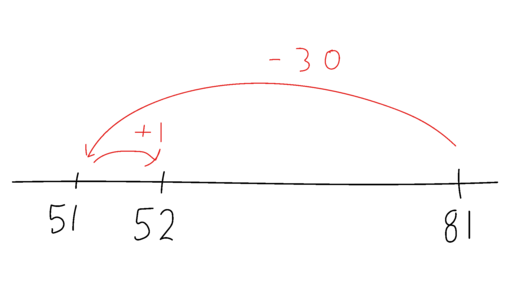
Den åbne tallinje er en vandret linje, hvorpå elever afsætter tal og handlinger på en uformel og tilnærmet måde. I figuren har en elev regnet $81 - 29$ ved at lave det om til $81 - 30$ og hoppe $30$ baglæns fra $81$ på tallinjen til $51$. Dernæst har eleven kompenseret og hoppet $1$ frem til $52$. Eleven har brugt en sekventiel og kompensationsstrategi og har tænkt direkte subtraktion.
Veksle-pladen
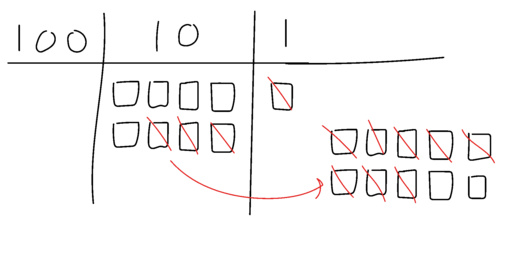
Veksle-pladen er et skema med kolonner for enere, tiere, hundrede osv., hvori elever kan repræsentere tal med fx centicubes, tegnede streger eller firkanter, eller tal. I figuren har en elev regnet $81-29$ ved at dele $81$ op i $8$ tiere og $1$ ener og tage $29$ væk: fjernet $2$ tiere, vekslet $1$ tier til $10$ enere og fjernet $9$ af disse. Resultatet står tilbage, dvs. $52$. Eleven har brugt en opdelingsstrategi og tænkt direkte subtraktion.
For at støtte en klasse i senere at kunne forstå og bruge de to repræsentationer kan klassen i begyndelsen af læringssporet bruge ikke-standardiserede måleenheder, fx stænger af centicubes eller perler på en snor, og base 10 materialer, fx centicubes og tierstænger. Når klassen er blevet fortrolige med disse repræsentationer og kan bruge dem i hverdagsproblemer, kan læreren introducere den åbne tallinje og veksle-pladen.
En klasse kan udvikle de tre strategier og tænkemåder i deres arbejde med hverdagsproblemer med støtte i den åbne tallinje og veksle-pladen og med støtte fra læreren. Når klassen har udviklet et bredt repertoire af strategier og tænkemåder og er blevet fortrolig med at tænke subtraktion ud fra den åbne tallinje og veksle-pladen, er det hensigten, at klassen begynder at tænke subtraktion ud fra tal og regneudtryk og gradvist løsriver sig fra den åbne tallinje og veksle-pladen. I den proces kan de problemer, som klassen arbejder med, med fordel skifte fra hverdagsproblemer til regneudtryk, og eleverne kan opfordres til at bruge tal og regneudtryk, når de selv regner. Idéen er, at klassen sidst i læringssporet kan tænke på og udvikle strategierne og tænkemåderne uden at støtte sig til den åbne tallinje og veksle-pladen, men kan gøre det ud fra tal og regneudtryk.
Der kan være forskelle i, hvornår eleverne er klar til at skifte repræsentationer, og nogle elever kan med fordel trække på den åbne tallinje eller veksle-pladen (eller skitser heraf) i længere tid. Når hverdagsproblemer, den åbne tallinje og veksle-pladen træder i baggrunden, påvirker de ikke længere elevernes valg af strategier, og eleverne kan derfor vælge mere fleksibelt. I sporets sidste faser er der derfor ikke en adskillelse mellem klassens udvikling af sekventielle og opdelingsstrategier.
Fase 1
Fase 1 tager udgangspunkt i klassens erfaringer med addition og subtraktion af tal op til 20 og deres tidligere tænkestrategier, såsom tag væk, op til 10 og ned til 10 (se Grundlag). I fasen støtter læreren klassen i at videreudvikle disse tre til de tre tænkemåder: direkte subtraktion, indirekte addition og indirekte subtraktion. Klassen kan med fordel arbejde med en bred vifte af hverdagsproblemer, der bl.a. har fokus på at måle og inddrage konkrete materialer, som fx ikke-standardiserede måleenheder, tierstænger og centicubes. Fasen er opdelt ift. klassens udvikling af sekventielle strategier og opdelingsstrategier. Hensigten med fasen er, at klassen udvikler de tre tænkemåder i tilknytning til sekventielle strategier og direkte subtraktion i tilknytning til opdelingsstrategier.
Med henblik på at udvikle sekventielle strategier kan klassen arbejde med målingsaktiviteter i enten sammenlign-, træk fra- eller del-helhed-situationer. Det er vigtigt, at eleverne måler i situationer, de kender, og at de oplever det som meningsfuldt at subtrahere resultaterne fra deres målinger. Klassen kan bruge ikke-standardiserede måleenheder, hvor 10’erne er angivet, fx antalskæder, perler på en snor (hvor perlerne skifter farver for hver 10. perle) eller stænger af centicubes (hvor centicubes skrifter farve for hver 10. perle), som de kan bruge til at finde forskelle mellem deres måleresultater ved at tælle eller hoppe op eller ned ad snoren eller stængerne. Eleverne kan derved bygge videre på deres tidligere strategier, og samtidig lægger brugen af snor eller centicubes-stænger op til at subtrahere med støtte i den åbne tallinje, der er fokus i fase 2.
Med henblik på at udvikle opdelingsstrategier kan klassen arbejde med træk fra- og del-helhed-situationer uden tierovergang, fx træk fra-situationen fra svømmehallen. Eleverne kan modellere situationerne med centicubes og tierstænger, hvilket kan støtte dem i at tænke om subtraktion som at tage $11$ væk fra $32$ (direkte subtraktion). Det er vigtigt, at klassen begynder at tænke subtraktion ud fra opdeling i tiere og enere.
Fase 1
At løse hverdagsproblemer med subtraktion med støtte i konkrete materialer og tegninger.
At modellere en situation vil sige at gengive dens handlinger eller relationer (National Research Council, 2001). Fx kan træk fra situationen fra svømmehallen modelleres ved at tælle en centicube op for hvert af de $32$ børn i svømmehallen og finde, hvor mange børn der er tilbage ved at fjerne en centicube for hvert af de $11$ børn, der er gået hjem.”
Fase 2
I fase 2 arbejder klassen med hverdagsproblemer for forsat at give eleverne mulighed for at tænke om subtraktion i relation til noget, de kender og kan forestille sig. Det kan støtte deres tænkning og inspirere til nye måder at løse problemerne på. Læreren kan introducere de to nye repræsentationer, den åbne tallinje og veksle-pladen ud fra klassens tidligere arbejde med ikke-standardiserede måleenheder og med centicubes og tierstænger. Fase 2 er også opdelt i forhold til klassens udvikling af sekventielle strategier og opdelingsstrategier, og klassen arbejder med hverdagsproblemer både med og uden tierovergang. I forhold til opdelingsstrategier er det centralt, at klassen udvikler forståelse af at opdele tal i tiere og enere og at veksle med støtte i veksle-pladen.
Fase 2
At løse hverdagsproblemer med subtraktion med støtte i tegninger og regneudtryk.
Fase 3
I fase 3 arbejder klassen med subtraktion mest som regnestykker og i mindre grad som hverdagsproblemer. I arbejdet med regnestykkerne kan eleverne forsat støtte sig til den åbne tallinje og veksle-pladen, men det er hensigten, at de – i denne og den næste fase – gradvist løsriver sig fra disse repræsentationer og i højre grad bruger tal og regneudtryk. Læreren kan støtte eleverne i at skrive og bruge tal i veksle-pladen fremfor streger og/eller firkanter. Elevernes valg og tilpasning af strategier er således i mindre grad påvirket af hverdagsproblemer og deres kontekster, men relaterer sig til tallene i et regnestykke og elevernes personlige valg. Elevernes valg af strategi vil derfor være mere fleksibelt, og eleverne kan i højere grad trække på både sekventielle og opdelingsstrategier. Det er centralt i fasen, at klassen deler, forklarer, sammenligner og taler om deres strategier, så eleverne opbygger et stort repertoire af forskellige strategier og en rutine i at overveje, hvilken strategi der er smartest til at regne et stykke og at tilpasse denne strategi.
Fase 3
At subtrahere fleksibelt med støtte i tegninger og regneudtryk.
Elevernes valg af strategier afhænger bl.a. af (1) regnestykket, fx hvad er ukendt, og hvilke tal indgår, (2) elevens karakteristika, fx alder og sikkerhed i én strategi og (3) sociokulturel kontekst, fx type af undervisningstilgang (Sunde, 2022).
Fase 4
I fase 4 er det hensigten, at klassen (så vidt muligt) slipper repræsentationerne fra de forrige faser og tænker i tal og regneudtryk. Hvis læreren vurderer, at de fleste elever i klassen kan subtrahere fleksibelt – det vil sige, at de har et bredt repertoire af strategier, og at de kan vælge og tilpasse en af disse strategier til et hverdagsproblem eller subtraktionsstykke – kan læreren vælge at introducere kolonne-metoden. Denne metode bygger på de erfaringer klassen har med sekventielle og opdelingsstrategier fra læringssporet. Det er vigtigt, at læreren introducerer metoden i tæt tilknytning til elevernes tænkning og deres hidtidige strategier, og at den ikke ses som et mål i sig selv. Metoden kan siges at være endnu en strategi i klassens repertoire, som eleverne kan bruge til at subtrahere flercifrede tal fleksibelt.
I alle faser er der forskelle i, hvornår eleverne udvikler de forskellige strategier, og hvornår de er klar til at bruge nye repræsentationer. Læreren skal derfor være opmærksom på disse forskelle og lade eleverne arbejde med strategier og repræsentationer, som falder dem naturlige. Omvendt vil der være elever, der ikke skifter til andre strategier eller repræsentationer på egen hånd, og læreren må derfor vurdere, hvornår det er hensigtsmæssigt at skifte for klassen og for den enkelte elev.
Det videre arbejde
Efter læringssporet er det oplagt, at en klasse arbejder videre med at udvikle deres strategier, så de også kan subtrahere $3$- og $4$-cifrede tal (eller større tal).
Læringssporet kan også danne overgang til indledende division, da eleverne kan bruge deres tænkning fra dette spor til at tænke om division som gentagen subtraktion. Klassen kan fx arbejde med målingsproblemer såsom ”Hvor mange $2$-liters flasker skal vi bruge til $10$ liter saft?”. Problemet kan løse med at trække $2$ fra $10$ så mange gange som muligt og tælle antallet af gange.
Fase 4
At subtrahere fleksibelt med brug af regneudtryk.