Grundlag – At addere etcifrede tal

Elevers regning med etcifrede tal er et af de mest udforskede områder i matematikkens didaktik (Fuson, 2003). I dag ses det at regne ikke kun som et middel til at producere et resultat, men i stadig højere grad som elevers vej til at forstå egenskaber ved tallene og regningsarterne (National Research Council, 2001). To resultater fra denne forskning udgør grundlaget for læringssporet.

Det første resultat udspringer af kvalitative studier i en række forskellige lande. Resultatet er, at selv om elever bliver undervist på forskellige måder, så lærer de typisk at regne med etcifrede tal ved at udvikle en række af stadig mere avancerede strategier, når de løser ofte simple aritmetiske problemer (National Research Council, 2001). Dette gælder specielt for elevers læring af addition med etcifrede tal. Her går progressionen fra uformelle tællestrategier til fleksibel brug af tænkestrategier (Fuson, 2003). Denne forskning viser altså, at eleverne ikke lærer at addere etcifrede tal ved at huske resultaterne udenad eller ved at træne brug af bestemte metoder. Det har man ellers troet og praktiseret i mange lande, fx USA og Canada (Fuson, 2003; National Research Council, 2001), og til dels også i Danmark.

Det andet resultat er, at problemer fra elevernes hverdag, som kan løses ved at bruge addition eller subtraktion – de såkaldte additive situationer – er vigtige, når eleverne skal udvikle strategier til addition, der giver mening for dem (Carpenter et al., 1999; Fuson, 2003).

Et andet eksempel på en del-helhed situation er den med Sofie: Sofie har 8 lakridser og 4 bolcher. Hvor meget slik har Sofie? Her er hver del kendt (8 lakridser og 4 bolcher), mens resultatet (helheden) er ukendt, og fokus er på relationen mellem de to dele og helheden. Situationen ville også handle om denne relation, hvis en del var ukendt, men problemet ville i så fald være et andet og langt sværere for yngre elever at løse. Relationen mellem delene og helheden er statisk i den forstand, at Sofie ikke får slik foræret eller selv giver noget slik væk. Der er altså ikke en forandring involveret i eksemplet. I modsat fald, hvis Sofie fx fik 6 bolcher af sin ven Jonas, ville der være tale om en læg til-situation.

Situationer med et ukendt resultat er nemmest for yngre elever at løse, og generelt er det sådan, at jo længere til højre et problem er i Figur 5, jo vanskeligere er det at løse. Af de fire typer af situationer er sammenlign-situationer typisk sværest for yngre elever at løse. De 11 problemer i Figur 5 er altså af forskellig sværhedsgrad. Desuden lægger de op til brug af forskellige repræsentationer og løsningstilgange, og de fejl, eleverne laver, er ofte også forskellige på tværs af problemerne (Verschaffel et al., 2007). Af disse grunde, og fordi de 11 problemer repræsenterer den vifte af situationer, der kan løses med addition eller subtraktion, som eleverne kan møde i deres omverden, er det vigtigt, at elevernes læring af addition og subtraktion af et- og flercifrede tal involverer dem alle.

Når yngre elever løser hverdagsproblemer, gør de det oftest ved at gengive de konkrete aktiviteter eller relationer i problemet og derigennem finde (nye) løsningsstrategier. Dette kaldes direkte modellering (National Research Council, 2001). Når elever modellerer en situation, vil de typisk udvikle strategier, der giver mening for dem ud fra problemets kontekst, og som lægger sig op af deres begrebsmæssige forståelse og matematiske tænkning (National Research Council, 2001). Det er derfor vigtigt, at eleverne ikke for tidligt afkræves en bestemt repræsentation i deres talarbejde, da det kan begrænse dem i at udvikle forståelser af både det egentlige problem og dets faglige indhold (Fuson, 2003). Det er helt afgørende for elevernes læring på både kort og lang sigt, at de udvikler for dem meningsfulde strategier til at løse overskuelige hverdagsproblemer, mens det er mindre vigtigt, om de regner hurtigt eller kan bruge standardmetoder tidligt. Forskning viser, at elever kan løse alle 11 problemer ved hjælp af modellering, så derfor er modellering en vigtigt tilgang (Fuson, 2003).

Udover at eleverne kan lære at genkende situationer i deres hverdag, der kan løses med addition og/eller subtraktion, så giver forskningen også tre andre væsentlige begrundelser for at tage udgangspunkt i additive situationer (Beishuizen & Anghileri, 1998; Council, 2001; Fuson, 2003; Verschaffel et al., 2007):

1. Eleverne kan leve sig ind i et hverdagsproblem og kan dermed tillægge dets matematikfaglige indhold en konkret og – for eleven – meningsfuld betydning. Dette er vigtigt, når elever skal udvikle nye strategier.

2. Eleverne kan modellere problemets aktiviteter eller relationer og derved finde (nye) måder at løse det på.

3. Eleverne kan udvikle deres tilgang til problemløsning, fordi de er nødt til at forstå det egentlige problem for at kunne løse det.

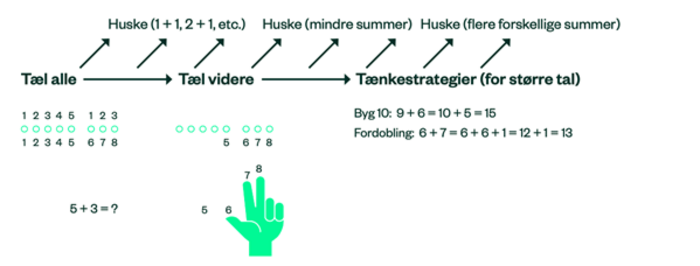
De tre strategier i progressionen er:

1. Tæl alle (engelsk: counting all):
   Elever tæller først den ene addend, fx ved at tælle (evt. tegne) et tilsvarende antal figurer, ting eller fingre, og dernæst den anden addend, for til sidst at tælle alle. I Figur 6 tegner eleven fx først fem små cirkler for 5 (den første addend) og dernæst tre små cirkler for 3 (den anden addend) og finder det samlede antal ved at tælle alle de små cirkler.  

2. Tæl videre (engelsk: counting on): 
   Elever tæller videre fra den ene addend og tæller den anden. Som Figur 6 viser, kan tæl videre ligge i umiddelbart forlængelse af tæl alle. I det øverste eksempel har eleven også talt addenderne op, men finder det samlede antal ved at tælle videre fra de fem første små cirkler ”5, 6, 7, 8” og tælle de næste tre cirkler, frem for at tælle alle cirklerne forfra. I det nederste eksempel kan eleven se 5 som et objekt, som eleven ikke længere behøver at tælle sig frem til, og eleven kan tælle videre fra 5 ved at bruge fingrene til at holde styr på antallet i den anden addend.

3. Tænkestrategier (engelsk: derived-fact strategies):
   Elever udvikler tænkestrategier ved at omskrive ukendte additionsstykker til stykker, de kender eller kan huske. De fleste elever husker let fordoblinger (fx 4 + 4, 7 + 7), addition med 1 (fx 4 + 1, 8 + 1) og addition med små tal (fx 2 + 3, 4 + 2). Det, eleverne husker, påvirker ofte den tænkestrategi, de udvikler i en given situation (Fuson, 2003). De mest hyppige og effektive tænkestrategier for etcifret addition er (Fuson, 2003; National Research Council, 2001):

   • Byg 10: Eleven bygger 10 af den ene addend ved at opdele den anden addend i en sum, hvor den første addends tier-ven indgår. I eksemplet med byg 10 i Figur 6 ved eleven, at det er smart og let at addere med 10. Eleven ved også, at tier-vennen til 9 er 1, og at 6 kan opdeles i 5 + 1. Eleven bruger denne viden til at omskrive stykket til et kendt additionsstykke 10 + 5.

   • Brug fordobling: Eleven kender det dobbelte af den ene addend og bruger dette til at omskrive additionsstykket til et velkendt stykke. I eksemplet med brug fordoblinger kan eleven både huske det dobbelte af 6 og en opdeling af 7 i 6 + 1. Ud fra dette omskriver eleven stykket til et kendt 6 + 6 + 1. 

At gå fra tæl alle til tæl videre kræver et stort spring. Det kræver, at eleven ikke kun kan se et tal som noget, man tæller med, men også kan se et tal som et objekt, der kan tælles og handles på. Det kræver også, at eleven kan se kardinaliteten af begge addender og holde regnskab med tællingen af den anden addend, fx ved brug af sine fingre (Baroody & Porpura, 2017) – se også Figur 6. Der er flere varianter af begge strategier, fx kan elever tælle videre fra den mindste eller største addend eller vælge én af dem tilfældigt, og de kan udvikle avancerede måder at holde regnskab på.

Tæl videre er en kraftfuld strategi. Studier viser, at 1. klasseelever – inklusiv elever med læringsvanskeligheder og ringe modersmålskundskaber – kan klare alle hverdagsproblemer knyttet til addition med etcifrede tal ved at tælle videre, hvis de vel at mærke er blevet undervist i strategien på en begrebsorienteret måde; altså med fokus på tal som et objekt (Fuson, 2003). Eleverne kan også lære at bruge strategien tilstrækkeligt hurtigt og præcist til at kunne anvende den ved alle slags beregninger med flercifrede tal (Fuson, 2003). Det er imidlertid vigtigt at understrege, at elever, der bliver ved med at tælle – også når tallene bliver større – formodentligt har problemer, der skal adresseres (Sunde, 2022).

Byg 10 er en vigtig strategi. Det er den, fordi strategien har fokus på tierovergange, som spiller en central rolle i beregninger med flercifrede tal for alle fire regnearter. Samtidig støtter strategien på en direkte måde elever i at udvikle en generel forståelse af vores positionssystem.

I praksis udvikler eleverne ikke først én strategi og så den næste, og de følger heller ikke læringsporet i samme rækkefølge med præcist de samme strategier eller i samme tempo. Elevernes brug af forskellige strategier er ofte overlappende, og brugen afhænger af flere ting fx regnestykket, elevens karakteristika og den sociokulturelle kontekst (Sunde, 2022). Det ses ofte, at elever har udviklet tænkestrategier til løsning af en bestemt type hverdagsproblemer, men bruger tællestrategier i nye problemer.

På trods af elevers overlappende udvikling af strategier viser forskning som sagt, at alle elever udvikler midlertidige og mellemliggende strategier, som minder om dem i læringssporet, og at de gør det uafhængigt af den undervisning, de modtager (Fuson, 2003). Elever, der ikke støttes i at udvikle tænkestrategier, vil dog ofte udvikle flere fejlagtige strategier, og der kan gå flere år, før de udvikler de mere sofistikerede tænkestrategier sammenlignet med elever, der får støtte (Fuson, 2003). Det er derfor vigtigt, at eleverne deltager i udvikling af regnestrategier, og at de støttes i deres udvikling af mere avancerede strategier og i deres forståelse af tallenes egenskaber og regnearterne (National Research Council, 2001). Det kan fx gøres gennem disse aktiviteter, der har inspireret læringssporet:

• At give eleverne muligheder for at bruge konkrete materialer og tegninger til at forklare strategier.
• At designe hverdagsproblemer, der understøtter brug af bestemte strategier.
• At designe hverdagsproblemer med store tal, så fx tællestrategier bliver vanskelige at bruge, og eleverne er nødt til at tænke i andre baner.
• At udvælge forskellige strategier, som eleverne har udviklet til løsning af hverdagsproblemer og drøfte fælles i klassen, hvordan og hvorfor de enkelte strategier virker.
• At sammenligne forskellige elevstrategier og diskutere deres forskelle og ligheder fælles i klassen (National Research Council, 2001).