Praksis – At addere etcifrede tal
De tidsmæssige rammer
Dette læringsspor kan anvendes tidligt i skoleforløbet. For nogle klasser kan det påbegyndes allerede i 0. klasse. For 1. klasser, der har erfaringer med at addere med brug af tællestrategier, kan fase 1 springes helt eller delvist over. Når læreren vurderer disse forhold, er det vigtigt at være opmærksom på, at elever, der er begyndt at udvikle tænkestrategier, skal have mulighed for at bygge videre på disse strategier – eleverne skal ikke begynde at addere ved at tælle igen.
Det kan være en god idé at strække læringssporet over 2-3 forløb af 1-2 ugers varighed frem til slutningen af 1. klasse eller starten af 2. klasse. I hvert forløb kan det være en fordel at supplere indholdet med fx lege og spil, der giver eleverne mulighed for fortsat at få rutine i at addere tal og i at samle og dele tal op. Det kan også være en fordel at supplere med andre repræsentationer end de foreslåede, såsom perler, kugler og billeder af ting, da det er vigtigt for klassens udvikling af talforståelse og strategier, at de møder forskellige repræsentationer og kan skifte og oversætte mellem dem. Mellem forløbene kan det være en god idé at holde klassens additionsstrategier vedlige og spørge ind til og lade eleverne sprogliggøre deres strategier og give dem mulighed for at kommentere hinandens strategier.
Det faglige udgangspunkt
Læringssporet tager udgangspunkt i de forståelser af tallene og erfaringer med at tælle og addere, som eleverne har fra børnehaven, 0. klasse og deres hverdag. Som vist i oversigten forudsætter læringssporet, at klassen har erfaringer med tal på tre niveauer.
Den første forudsætning er, at klassen kender tallenes navne fra 1 til 20 og kan skrive de fleste af disse tal. Det er en fordel, hvis eleverne har erfaringer med tælleremser, fx 2, 4, 6, … eller 10, 20, 30, … som de kan bruge til at huske talnavnene. Det er en god idé, hvis klassen – sideløbende med læringssporet – lærer tallenes navne efter 20 og at skrive disse tal.
Den anden forudsætning er, at klassen har erfaringer med at tælle ting og bestemme antal, bl.a. ved at samle i bunker og tælle. Det vil sige, at eleverne:
- kan tælle ting i en mængde ved at knytte ét tal – det næste i talrækken – til hver ting og lave en 1-1 korrespondance
- ved, at det sidste talte tal fortæller, hvor mange ting der er i mængden (se tema ”At tælle”).
Den tredje forudsætning er, at klassen kan genkende små antal uden at tælle – at de kan subitize. Denne forudsætning er mindre vigtig end de to andre, og den kan også styrkes i elevernes arbejde med læringssporet.
Fase 1
I fase 1 arbejder klassen med hverdagsproblemer, som de kan modellere og løse med støtte i konkrete materialer, såsom deres fingre, agern, kastanjer og centicubes. Hensigten med fasen er, at klassen får konkrete erfaringer med at addere ved at tælle og udvikler strategier, især tæl videre. Det er derfor vigtigt, at klassen ser forskellige strategier til at løse hverdagsproblemerne, og at de får mulighed for at sammenligne og tale om deres strategier med hinanden og med læreren. Det kan være en god idé at starte med additioner uden tierovergang og løbende øge problemernes sværhedsgrad. Læreren kan med fordel støtte eleverne i at formulere det regneudtryk, som hører til problemet – enten før eller efter klassen har løst det. Da de fleste elever endnu ikke kan læse, kan læreren iscenesætte hverdagsproblemerne via en fortælling eller dramatisering.
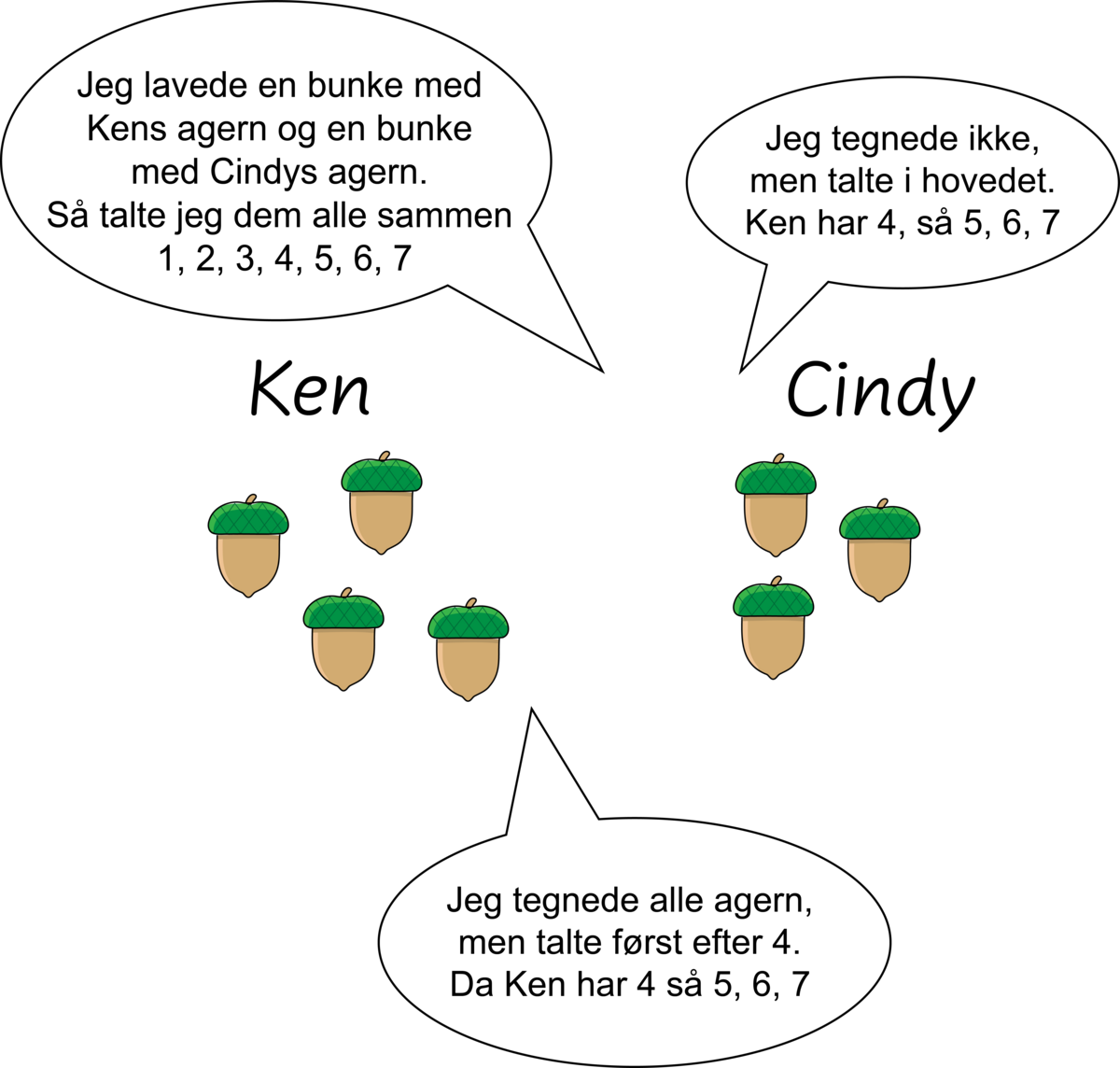
Den opdigtede dialog omkring Ken og Cindys agern skal illustrere, hvordan læreren opmuntrer eleverne til at forklare de strategier, de har brugt, og at få øje på forskelle og ligheder mellem dem. Dialogen er inspireret af Takahashi (2021):
Fase 1
At løse hverdagsproblemer med addition med brug af tællestrategier og støtte i konkrete materialer.
Ken og Cindys agern
Læreren præsenterer denne læg til-situation mundtligt for eleverne:
Ken samler 4 agern, og Cindy samler 3 agern. Hvor mange agern har de samlet tilsammen? Forklar, hvordan du har fundet ud af det.
Eleverne bruger konkrete materialer, tegner og noterer i deres kladdehæfter. Læreren udvælger tre elevforslag (se Figur 2), som eleverne præsenterer i en klassesamtale:
Lærer: Hvad er det for et regnestykke vi skal løse for at finde ud af, hvor mange agern Ken og Cindy har samlet?
Clara: Han har 4 … Cindy 3 … lægge dem sammen?
Lærer: Ja, vi skal lægge deres agern sammen. Det skriver vi som 3 + 4 [skriver på tavlen]. Vi bruger plustegnet [peger på tegnet] til at vise, at vi skal lægge sammen. Hvordan kan vi regne 3 + 4? Emil, hvad tænker du?
Emil: Jeg lavede Kens agern her [peger på en bunke af 4 agern] og Cindys her [peger på en anden bunke med 3 agern]. Og så 1, 2, 3, 4, 5, 6, 7 [tæller højt, mens han peger på agernene en efter en].
Lærer: Du talte først Kens agern [tegner 4 prikker på tavlen og skriver Ken ovenover] og derefter Cindys agern [tegner 3 prikker på tavlen og skriver Cindy ovenover]. Og så talte du alle deres agern [1, 2, … tæller, mens han peger på prikkerne]. Er I enige i, at man kan gøre som Emil?
Sofie: Ja, Emil talte dem alle … så det er rigtigt.
Lærer: Du siger, at Emils metode kan bruges, fordi Emil først finder både Kens og Cindys agern og dernæst tæller alle deres agern. Er der nogen, der har brugt samme metode som Emil? Ræk hånden op [tæller 1, 2, 3, 4, 5, 6 elever].
Lærer: Ok, der er flere, der har gjort som Emil, men der er også nogle, der har løst stykket på en anden måde? Ja, Laura.
Laura: Jeg tegnede deres agern [peger på tavlen], men talte kun Cindys … vidste Ken har 4, så 5, 6, 7 [tæller prikkerne for Cindys agern].
Lærer: Ok, så Laura siger, at hun vidste, at Ken havde 4 agern uden at tælle – og så tæller hun videre fra Kens 4 agern, når hun lægger Cindys 3 agern til [peger på hver af de 3 prikker, mens læreren tæller]. Det var smart, at Laura ved, hvor mange agern Ken har uden at tælle. Er der nogen, der har løst opgaven på en tredje måde?
Muhammed: Jeg gad ikke tegne. Ken har 4, så jeg talte i hovedet, 5, 6, 7 [viser med fingrene, hvordan han holdt styr på Cindys 3 agern].
Lærer: Ok, så Muhammed gjorde det på en helt tredje måde. Er der nogle, der vil forklare, hvad Muhammed gjorde?
Rahat: Han kan … ligesom se Kens agern … inde i sit hoved ... så tæller han Cindys agern med fingrene, 5, 6, 7 [tæller på sine fingre].
Lærer: Ok. Nu har vi set tre tællemåder til at regne 4 plus 3. Der var Emils, der var Lauras, og der var Muhammeds. Vi skal sammen prøve de tre måder med et nyt stykke. Hvad hvis Ken havde 5 agern og Cindy havde 7 agern? Bagefter spørger jeg jer, hvad der er ens, og hvad der er forskelligt ved de tre måder. Og hvilken måde, I synes, er smartest.
Dialogen fremhæver fire pointer.
For det første viser den, hvordan læreren kan støtte klassen i at genkende og opskrive situationen som et additionsstykke.
For det andet udvælger læreren tre elevforslag, der repræsenterer tre stadig mere sofistikerede måder at tælle på. Stort set alle elever i 1. klasse vil kunne finde resultatet ved at tælle alle ligesom Emil. Det er sværere at tælle videre, som Laura og Muhammed gør – og særligt at løsrive sig fra konteksten som Muhammed. Tæl videre er sværere, fordi eleverne skal kunne se Kens 4 agern som noget, de ikke behøver tælle op, men kan handle direkte på, og samtidig skal de holde styr på det antal, som de tæller videre (3 agern) (se Grundlag). Læreren skal være opmærksom herpå og støtte eleverne fx ved – som læreren i dialogen – at gentage eller bede andre elever om at gentage hver enkelt strategi, fremhæve kendetegn ved de tre strategier, bede eleverne om at afprøve dem på et nyt stykke og efterfølgende tale med dem om, hvilke forskelle og ligheder de ser ved strategierne. De fleste elever vil med en sådan lærerstøtte kunne udvikle tæl videre uden store problemer.
For det tredje tæller både Laura og Muhammed videre fra det første tal 4, som også er det største. Det giver færre tælleoperationer og er derfor hurtigere, end hvis de var startet med 3. Det er imidlertid ikke klart, om de valgte at starte med 4 af denne grund, eller om det var, fordi 4 stod først i stykket. Læreren kan vælge at fremhæve denne pointe, når eleverne skal addere 5 + 7 ved hjælp af de tre strategier og her prøve at finde mening i, at 5 + 7 og 7 + 5 giver samme resultat. Det er generelt sværere for elever at tælle alle i situationer, hvor det mindste tal nævnes først, fordi elever typisk tæller videre fra det første tal, og derfor skal de holde styr på et større antal, når de tæller videre.
For det fjerde er der i en klasse ofte en bred variation af tællestrategier: tæl alle, som Emil og ca. ¼ af eleverne brugte i dialogen, tæl videre fra det mindste eller største tal, tæl videre fra et tilfældigt tal. Der vil også være elever, der begynder at bruge fordoblinger eller at opdele og samle tallene og bruge byg 10. De kan fx have tænkt 5 + 7 = 5 + 5 + 2 = 10 + 2 = 12. Disse elever skal naturligvis ikke bremses i deres udvikling samtidig med, at elever der ikke er lige så langt skal have mulighed for i denne fase at få erfaringer med tællestrategier som dem beskrevet i dialogen. Som inspiration til at differentiere undervisningen eller støtte udvalgte elever i at udvikle tæl videre kan læreren overveje:
- at give elever, der har vanskeligt ved at udvikle tællestrategier, mulighed for at modellere situationen med de ting, den handler om, fx agern som i dialogen. Det vil gøre det lettere for eleverne at leve sig ind i situationen.
- at fokusere på små tal i starten af fase 1, så eleverne kan koncentrere sig om udfordringer knyttet til selve additionen. Senere – eller for udvalgte elever – kan tallene gøres større og aktivitetens sværhedsgrad øges.
- at udvælge aktiviteter som Hvor mange har jeg i hånden?, der kan støtte alle eller udvalgte elever med at udvikle tæl videre.
- at lade elever, der har brug for ekstra udfordringer, arbejde med sammenlign-situationer (evt. inden for samme kontekst), da disse situationer generelt er sværere at løse.
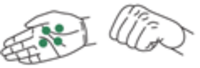
Hvor mange har jeg i hånden?
En læg til-situation med en ukendt addend kan – som præsenteret på tegningen – støtte elever i at tælle videre. Hvis en elev fx får at vide, at der er 7 perler i alt, så støttes eleven i at tælle videre fra de 4 i hånden og op til 7. Inspireret af Caldwell et al. (2014, s. 32).
Fase 2
I fase 2 arbejder klassen videre med hverdagsproblemer. Hensigten er, at klassen udvikler de tre forudsætninger, der er nødvendige for, at de kan udvikle tænkestrategier: at dele tal op i summer, at finde tier-venner og at addere 10 og etcifrede tal. Især den første forudsætning er vigtig. For at støtte klassen i at udvikle denne kan læreren introducere tier-rammen (se Tilgang), fx ved at vise, hvordan klassen kan bruge den til at løse et hverdagsproblem, som de kender og lige har arbejdet med.
I fase 2 kan klassen med fordel arbejde med del-helhed-situationer, der lægger op til en naturlig opdeling af et tal. Det kan være situationer med passagerer i et tog i to etager – et dobbeltdækkertog – hvor togets samlede antal passagerer kan opdeles i dem på det nederste dæk og dem på det øverste dæk. Det kan også være situationer med passagerer i en dobbeltdækkerbus, sovepladser i køjesenge, beboere i toetageshuse og marsvin i to forskellige bure. Eksemplet med dobbeltdækkertoget er inspireret af Gravemeijer et al. (2000) og skal vise, hvordan eleverne ved hjælp af tier-rammen udvikler forskellige og for dem meningsfulde løsninger, og at nogle elever også kan se en systematik i løsningerne.
Fase 2
At løse hverdagsproblemer med addition ved at dele tal op og med støtte i tegninger.
Dobbeltdækkertoget
Eleverne starter med at bruge tier-rammen til at modellere situationer, hvor resultatet er ukendt (se Grundlag), fx:
Der er 4 personer på togets øverste dæk og 5 personer på dets nederste dæk. Hvor mange personer er der med toget?
Når klassen har modelleret problemet med tier-rammen og er blevet enige om, at der er 9 passagerer med toget, kan læreren følge op med det egentlige problem, hvor kun resultatet er kendt:
Hvordan kan I vise, at der er 9 personer med dobbeltdækkertoget?
Eleverne arbejder alene eller i små grupper med at modellere og løse denne situation med støtte i tier-rammen. Læreren samler op på elevernes arbejde i en fælles klassesamtale:
Lærer: Hvem vil starte med at vise, hvordan de har brugt tier-rammen til at vise, at der er 9 personer med dobbeltdækkertoget?
Emil: Byttede bare rundt på 4 og 5.
Lærer: Prøv at vise, hvad du har tænkt på en af de tier-rammer, jeg har tegnet på tavlen [lærere har tegnet 10 tier-rammer på tavlen].
Emil: Først var der 4 personer over [udfylder 4 felter i den første tier-ramme] og 5 under [udfylder 5 felter]. Så byttede jeg dem bare rundt [udfylder på lærerens opfordring en ny tier-ramme: 5 felter øverst og 4 felter nederst].
Lærer: Ok, det ser smart ud. Men hvordan kan vi vide, om der stadig er 9 personer med bussen? Silas?
Silas: Der er 1 mindre end 10.
Lærer: Er der nogle, der er enig med Silas og vil forklare med deres egne ord? Ja, Sofus?
Sofus: I den første del … er der 5 og 5, det er 10, men der mangler en, så 9.
Lærer: OK, hvis I ser på den første del af tier-rammen, så er der 5 øverst og 5 nederst, det er 10, men nederst har vi ikke farvet den sidste, så derfor er der 9 personer. Er I andre enige?
Flere elever: Ja!
Laura: Der var 9 før, og vi har jo ikke fjernet nogle, så …
Lærer: Ja. Så vi ved nu, at 9 personer kan sidde, så der er 5 øverst og 4 nederst, men de kan også bytte plads, så der er 5 personer nederst og 4 øverst. Det var smart. Andre måder, der kan være 9 personer med bussen?
Josefine: De kan alle sammen sidde foroven.
Lærer: Prøv lige at tegne det [Josefine udfylder den tredje tier-ramme]. Kan du komme i tanke om en anden måde? Prøv at tænke i det, som Emil sagde med at bytte rundt.
Josefine: Nåee. De kan også alle være forneden [udfylder den fjerde tier-ramme].
Andreas: Der kan også være 6 over og 3 under [udfylder den femte tier-ramme].
Lærer: Hvordan ved du det?
Andreas: Du kan flytte en herned [peger på en af de 6 og ’flytter’ den ned til de 3], så er det lige som den [peger på anden tier-ramme med 5 øverst og 4 nederst].
Lærer: Er der nogle, der kan forklare, hvad Andreas gjorde for at få 6 og 3?
Muhammed: Han flyttede en herfra [peger på den nederste række i den anden tier-ramme] og op [peger på den øverste række] … uden at fjerne nogen.
Laura (ivrig): Man kan også flytte to, så bliver der 7 og … og 2.
Rahat: Der kan også sidde 1 person foroven, og …
Der er to centrale pointer med dialogen.
For det første viser dialogen, at tier-rammen kan støtte eleverne på forskellige måder: 1) Det giver mening for eleverne at opdele 9 på forskellige måder, da de kan relatere situationen og tier-rammen til noget, de kender fra deres hverdag. 2) Tier-rammen kan støtte eleverne i at forklare deres opdelinger af 9 og i at begrunde, at opdelingerne er korrekte. 3) Tier-rammen kan inspirere til nye opdelinger, fx når Andreas laver 6 og 3 ved at flytte en passager fra nederste til øverste række i en tidligere tier-ramme med 5 og 4 – et system som Laura hurtigt fanger.
For det andet viser dialogen, at der kan opstå muligheder for, at eleverne kan få erfaringer med vigtige regler for addition, særligt den kommutative lov, fx $5+4=4+5$. Læreren omtaler den med elevernes egne ord som at ”bytte rundt” på passagerne på de to dæk og støtter deres begyndende forståelse af reglen ved at bede eleverne om at begrunde den og at opmuntre, fx Josefine, til at bruge den. Det er essentielt, at elever får erfaringer med netop denne regel for at kunne udvikle tænkestrategier.
I fase 2 er det vigtigt, at klassen får erfaringer med at opdele etcifrede tal i summer af to tal, fx 8 = 4 + 4 og 8 = 7 + 1, i stil med dem beskrevet i eksemplet med dobbeltdækkertoget. Derudover er det også vigtigt, at klassen får erfaringer med de to andre forudsætninger for at udvikle tænkestrategier, nemlig at eleverne kan:
-
finde tier-venner, fx 6 + 4 = 10 og 5 + 5 = 10.
-
finde summen af 10 og et etcifret tal, fx 10 + 4 = 14, 10 + 7 = 17.
Læreren kan støtte klassen i at udvikle de tre forudsætninger gennem aktiviteter som:
-
At undersøge, hvordan 10 personer kan sidde i dobbeltdækkertoget:
Klassen kan undersøge det samme problem som i eksemplet med dobbeltdækkertoget. Det kan støtte eleverne i at kunne forstå, finde og huske tier-venner. -
At undersøge, hvor mange måder et tal, fx 9, kan deles op i summen af to tal:
Denne aktivitet er en oplagt forsættelse af eksemplet med dobbeltdækkertoget. I dialogen er der ved at udvikle sig en systematik i elevernes løsningsforslag, som kan bruges som argument. Elevernes løsningsforslag kan fx skrives op i rækkefølge efter antallet af passagerer på det øverste dæk. Ud fra skemaet kan læreren og eleverne argumentere for, at de har fundet alle opdelingerne. -
At undersøge, hvordan ?? personer kan sidde i dobbeltdækkertoget:
Klassen kan undersøge det samme problem som i eksemplet med dobbeltdækkertoget, men med andet etcifret antal personer. Det kan støtte eleverne i at dele etcifrede tal op. Hvis antal personer er et tocifret tal, kan eleverne støttes i at finde tier-venner og summen af 10 og et etcifret tal. I så fald kan en tyver-ramme bruges, som består af to rammer med 10 felter i hver. -
At undersøge, hvad der sker, når etcifrede tal adderes med 10:
Klassens forskellige løsninger kan skrives på tavlen, og sammen med læreren kan klassen opdage en regel for addition med 10, som de kan formulere sammen. -
At lave opdelinger og tier-venner med konkrete materialer:
Særligt elever, der er udfordrede, kan støttes ved at lave opdelinger og finde tier-venner med konkrete materialer såsom Numicon, Base 10 eller penge.
Numicon er små plader af plastik eller mosgummi med fra 1 til 10 huller. Hullerne sidder to og to over hinanden, og de ulige tal har et ekstra hul.
Fase 3
I fase 3 arbejder klassen også med hverdagsproblemer, men nu med fokus på at udvikle tænkestrategier, særligt byg 10 og brug fordoblinger (se Grundlag). Hensigten er, at klassen opbygger et bredt repertoire af sådanne tænkestrategier. Klassen kan støtte sig til tier-rammen i deres arbejde, men for at støtte dem i at løsrive sig fra tier-rammen i næste fase kan læreren bruge tal og regneudtryk sammen med den og opfordre eleverne til at gøre det samme.
Klassen skal se forskellige måder at tænke addition og forklare deres tænkning og strategier. Ofte opstår strategierne, når eleverne arbejder ud fra deres egne idéer, og det bliver en opgave for læreren at gribe de idéer, som kan føre klassens tænkning fremad, og gøre dem til genstand for klassens drøftelser og refleksioner.Det skal eksemplet med forsættelsen af dobbeltdækkertoget vise, der er inspireret af Gravemeijer et al. (2000).
Fase 3
At addere to etcifrede tal fleksibelt med brug af tænkestrategier og støtte i tegninger og regneudtryk.
Fortsættelse af dobbeltdækkertoget
Klassen arbejder med denne læg til-situation:
Der er 8 personer med dobbeltdækkertoget og 7 personer mere stiger på. Hvor mange er der med toget?
Eleverne har brugt tier-rammen, og de fleste har lagt 8 i dens øverste række og 7 i dens nederste. Læreren har udvalgt tre forskellige elevforslag til en fælles klassesamtale:
Lærer: Hvad er det for et regnestykke, I skal regne for at finde ud af, hvor mange personer der er i toget. Først er der 8 med og, senere kommer der 7 mere?
Andrea: Det er 8 og så … lægge 7 til.
Lærer: Hvordan kan jeg skrive det?
Andrea: 8 og så … plus … 7 og så, hvor meget det er.
Lærer: Så 8 plus 7 er lig med [skriver på tavlen: 8 + 7 = __]. Hvordan har I tænkt?
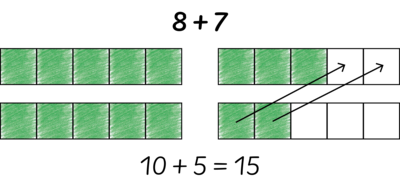
Donald: Jeg så 15 [tegner 8 øverst og 7 nederst i en tier-ramme på tavlen], fordi jeg så 5 plus 5 [peger på tier-rammen], og jeg ved, det giver 10 … og så 3 mere her [peger på de sidste tre farvede felter i øverste række] og 2 mere [peger de to sidste i nederste række]. Så 11, 12, 13 [tæller de tre øverste] og 14, 15 [tæller de to nederste].
Lærer: Ok, Donald siger, at han så 15. Han så først 2 grupper af 5 [peger på de 5 første felter i hver ramme], og han vidste, at 5 plus 5 er 10. Så så han, at der her var 3 mere [peger på de sidste 3 farvede felter øverst] og 2 mere her [peger på de 2 forneden], og det gav 5. Så 5 + 5 + 3 + 2 = 15 (se Figur 3). Hvad skal vi kalde Donalds idé?
Andrea: 5. Donald fandt 5 og 5 og til sidst 3 og 2 og 5 mere.
Lærer: Godt set, Andrea. Vi kalder Donalds idé for byg 5. Sofus, hvad har du tænkt?
Sofus: Jeg lagde 2 til 8, så 10, og så var der 5 tilbage, så 15.
Lærer: OK, så Sofus har også samlet i grupper, men med 10 i hver. Sofus så, at der manglede 2 i øverste række for at få 10, så han tog 2 fra den nederste række og lavede 10. Så var der 5 tilbage i nederste række. Den lagde han til 10 og fik 15 (se Figur 4). Hvordan fik du den idé, Sofus?
Sofus: Jeg så bare … nemt at lave 10, bare 2 mere.
Lærer: Ok, hvad skal vi kalde Sofus’ idé?
Donald: Byg 10? Sofus gør næsten det samme som mig.
Lærer: Godt forslag, Donald. Er der nogen, der har gjort det på en anden måde? Ea?
Ea: Jeg sagde 8 og 8. Det er 16 og så én mindre.
Lærer: Ok, så Ea vidste, at hvis der var 8 personer med toget, og der kom 8 nye, så ville der være 8 plus 8, altså 16 personer med toget. Men der kom jo ikke 8, men 7 nye personer på, så Ea fik talt en person for meget med. Derfor træk hun én fra. Hvordan fik du den idé, Ea?
Ea: Jeg kunne bare huske, at 8 plus 8 er 16, og så tænkte jeg, at det lignede.
Lærer: Hvad skal vi kalde Eas idé?
Rahat: Plus sig selv.
Lærer: Super, Rahat – vi kalder Eas idé for Plus sig selv. Ok. Nu har vi set tre måder til at regne 8 plus 7. Der var Donalds, som vi kaldte byg 5. Der var Sofus’, som vi kaldte byg 10, og så var der Emmas, som vi kaldte plus sig selv. I skal nu bruge hver af de tre måder til at regne et nyt stykke. Hvor mange personer er med toget, hvis der var 7, og der kom 6 mere? Bagefter spørger jeg jer, hvad der er ens, og hvad der er forskelligt ved de tre måder.
Dialogen fremhæver to pointer. For det første viser den, at elevernes idéer til at samle i grupper kommer fra deres brug af tier-rammen. Det støttes af rammens opdeling i to rækker af fem foroven og forneden og dens muligheder for at flytte rundt på tallene. Læreren støtter det også ved at udvælge de to elevstrategier, der handler om at gruppere, og at tydeliggøre deres forskelle.
For det andet viser dialogen, at tænkestrategier kan opstå, når elever arbejder undersøgende ud fra deres egne idéer. Læreren i dialogen vælger at fokusere på tre af de strategier, som opstod – at bygge 5 eller 10 og bruge fordobling – da de er særligt vigtige for klassens udvikling af additionsstrategier. Læreren fremhæver kendetegn ved strategierne, gentager elevernes forklaringer mundtligt, navngiver strategierne sammen med klassen og skriver dem i en blanding af tier-rammen, tal og regneudtryk på tavlen. Klassen gives således muligheder for at se og tale om de tre strategier og at afprøve og sammenligne dem. Hvis ingen elever havde foreslået byg 10 eller brug fordobling, kunne læreren havde foreslået dem som sine egne strategier.

Udover at udvikle tænkestrategier, særligt byg 10, er det i fase 3 vigtigt, at klassen får erfaringer med at bruge, tale om og sammenligne deres strategier, som vist i eksemplet. Klassen kan med fordel arbejde med dobbeltdækkertog-problemet (eller et lignende problem), men kan senere udfordres med andre problemer, da det kan føre til at klassen udvikler andre tænkestrategier. Klassen (eller udvalgte elever) kan udfordres ved at bruge større tal (evt. tocifrede tal) i problemerne, at arbejde med regneudtryk frem for hverdagsproblemer og at addere uden støtte i tier-rammen.
Fase 4
I fase 4 arbejder klassen mest med additionsstykker, der er skrevet som regneudtryk. Der er fokus på, at klassen fortsat opbygger deres repertoire af tænkestrategier, men særligt på at de kan vælge en strategi fra deres repertoire og tilpasse den til et additionsstykke. Hensigten er altså, at klassen kan addere fleksibelt med brug af tænkestrategier og støtte i regneudtryk. Klassen skal derfor have mulighed for at vise, forklare, sammenligne og tale om deres strategier – særligt med fokus på, hvilke strategier der er smarte at bruge til bestemte stykker og begrunde hvorfor.
For at give klassen mulighed for dette kan læreren på baggrund af deres arbejde med additionsstykker stille spørgsmål i stil med disse (strategier kan evt. skiftes ud med regnemåder):
-
Er nogle strategier nemmere at bruge end andre? Og hvorfor?
-
Ligner nogle strategier andre strategier, I kender?
-
Hvordan ligner de hinanden?
-
Hvordan er strategierne forskellige fra hinanden?
-
Hvilke strategier passer bedre til dette additionsstykke end andre strategier? Hvorfor?
Nedenfor gives fire eksempler på, hvordan læreren kan stille disse spørgsmål, og hvilke pointer der kan fremdrages.
Fase 4
At addere to etcifrede tal fleksibelt med brug af tænkestrategier og støtte i regneudtryk.
Eksempel 1: Hvornår er det smart at bruge fordoblinger?
Klassen har arbejdet med 8 + 7. Emma har bygget 10, mens Ismal har brugt fordobling. Læreren kan sige noget i stil med:
Lærer: Prøv at se på Emmas og Ismals løsninger. Emma har bygget 10 ved at tage 2 fra 7 og lægge til 8, så hun får 10 + 5 [peger på Emmas løsning]. Ismal har brugt fordoblinger. Han ved, at 8 + 8 er 16, og så har han trukket én fra, fordi det var 8 + 7. Begge måder er smarte, når I skal regne 8 + 7. Nu skal I prøve at regne et nyt stykke 4 + 8. Først med Emmas måde og derefter med Ismals måde. Så drøfter vi bagefter, hvilken måde der er smartest, og I skal prøve at forklare, hvorfor den ene er smartere end den anden.
Eksempel 2: Hvorfor giver brug af fordoblinger samme resultat?
Klassen har arbejdet med 8 + 9. Både Bo og Else har brugt fordobling, men på forskellige måder: Bo har fordoblet 8, mens Else har fordoblet 9. Læreren kan sige noget i stil med:
Lærer: Prøv at se på Bos og Elses løsninger. Bo og Else har tænkt på samme måde – de har begge brugt fordoblinger eller ”plus sig selv”, som vi kaldte den sidst – men de har gjort det lidt forskelligt. Bo har regnet 8 + 8 og lagt 1 til, mens Emma har regnet 9 + 9 og trukket 1 fra. De får begge 17, så begge måder må kunne bruges. I skal nu bruge hver af deres måder på et nyt stykke 5 + 4. Hvis I også får samme resultat, skal I prøve at forklare, hvorfor I kan regne det på begge måder.
Eksempel 3: Skriv det som et regneudtryk
Klassen har arbejdet med 8 + 9. Muhammed forklarer, hvordan han regnede: ”jeg havde … jeg tog 9 væk. Jeg mener, jeg tog 2 væk fra 9 og lagde dem til de 8, og det gav 10. Så havde jeg 7 mere”. For at støtte oversættelsen til et regneudtryk kan læreren fx sige:
Lærer: Emma, vil du prøve at gentage, hvad Muhammed sagde? Så skriver jeg det op som et regneudtryk på tavlen samtidig med, at du siger det [skriver 9 + 8 = 7 + 2 + 8 = 7 + 10 = 17 på tavlen]. Muhammed gjorde noget smart: han byggede 10, fordi det er nemt at regne med [peger på udtrykket]. I skal nu regne 8 + 5 på samme måde som Muhammed, og beskriv derefter det, I gjorde, med et regneudtryk.
Eksempel 4: Kan man bygge 10 på flere måder?
Klassen har arbejdet med 8 + 4. Sofie og Mikkel har begge bygget 10, men på forskellige måder. Læreren kan sige noget i stil med:
Lærer: Prøv at se på Sofies og Mikkels løsninger. Jeg skriver dem op med regneudtryk, så I nemmere kan sammenligne dem [skriver Sofies løsning: 8 + 4 = 8 + 2 + 2 = 10 + 2 = 12 og Mikkels løsning: 8 + 4 = 2 + 6 + 4 = 2 + 10 = 12]. Prøv at tale med jeres sidemakker om, hvordan de to løsninger ligner hinanden, og hvordan de er forskellige. Det ser ud til, at man kan bruge begge måder, da de giver samme resultat. Kan I prøve at forklare hvorfor?
I fase 4 er det vigtigt, at klassen kan bruge en bred vifte af strategier, forklaringer og begrundelser. I eksemplerne nævnes kun tænkestrategier, men det er også oplagt at sammenligne tællestrategier og tænkestrategier og tale om, hvilke der er smartest. Det bør fremgå klart, at tænkestrategier er smartest, og at læreren via sådanne sammenligninger og drøftelse kan støtte flere og flere elever i at udvikle tænkestrategier og bruge dem frem for tællestrategier. Som sagt er det vigtigt, at elever ikke bliver ved med at tælle, da det kan være tegn på vanskeligheder. Hvis nogle elever har svært ved at regne additionsstykker skrevet som regneudtryk, kan læreren reformulere dem som hverdagsproblemer, og/eller de kan støtte sig til tier-rammen, når de regner stykkerne. Det er vigtigere, at eleverne udvikler tænkestrategierne (evt. lidt langsommere end deres kammerater), end at de bliver ved med at tælle på regneudtryk.