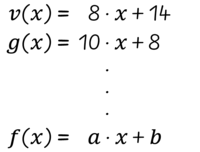Tilgang – At sammenligne lineære funktioner

De tre vigtigste idéer i læringssporet er:

1. Funktionssituationer
2. Repræsentationer af funktioner
3. Korrespondancesammenhæng og samvariation.

I faserne 1-3 arbejder klassen med udgangspunkt i funktionssituationer. Læreren udvælger funktionssituationer, som eleverne kan forestille sig og leve sig ind i på en meningsfuld måde. Funktionssituationerne skal også give et godt grundlag for, at klassen kan arbejde med centrale aspekter ved lineære funktioner. Det kan derfor være en god idé at vælge funktionssituationer, der er renset for ’støj’, fx måleusikkerhed, for ikke at aflede elevernes opmærksomhed fra det matematikfaglige indhold. En funktionssituation kan være både et hverdagsproblem og en matematisk problemstilling. Læreren kan også bruge funktionssituationer, som klassen tidligere har arbejdet med. Her er eksempler på fire mulige funktionssituationer.

I de fire eksempler øges sværhedsgraden gradvist. Eksemplet 1, Isvafler, er det letteste, da det kun involverer addition af naturlige tal. De øvrige eksempler involverer heltal (Lodsedler), rationale og reelle tal (Afstand og Omkreds) og subtraktion af tallene (Lodsedler) eller af den uafhængige variabel (Afstand og Omkreds). Det er tanken, at funktionssituationernes sværhedsgrad øges gradvist på denne måde efter hvert gennemløb af faserne 1-3, men samtidig skal den også være afstemt med klassens faglige niveau.

Det er vigtigt, at klassen i flere af gennemløbene arbejder med lineære sammenhænge, hvor den uafhængige variabel er et reelt tal, og graferne derfor er rette linjer og ikke punktgrafer (som i Afstand og Omkreds). Det kan også være sammenhænge, hvor noget udvikler sig over tid.

I fase 3 arbejder klassen med at sammenligne to lineære sammenhænge, der referer til den samme kontekst, fx at købe isvafler. I Afstand og Omkreds er der ikke formuleret en sammenlignelig situation, men for Afstand kan det være et andet sted i Danmark, hvor afstanden mellem fyret og havet samt havets ’hastighed’ fx begge er mindre, og for Omkreds kan det være en anden type figur, fx en trekant.

I læringssporet arbejder klassen med to forskellige sammenhænge mellem den uafhængige variabel $x$ og den afhængige variabel $y$. I korrespondancesammenhæng er fokus på, hvordan $y$ afhænger af $x$, mens fokus i den anden sammenhæng – samvariation – er på, hvordan $x$ og $y$ varierer sammen.

I fase 1 arbejder klassen med lineære sammenhænge ud fra funktionssituationer, som de oversætter til tabeller og regneudtryk og videre til punktgrafer. Isvafler er et eksempel på en funktionssituation, som klassen måske kender:

I iskiosken Vaflen skal man betale $8$ kr. for en kugle is og $14$ kr. for en vaffel. I iskiosken Gammeldaws skal man betale $10$ kr. for en kugle is og $8$ kr. for en vaffel. Beskriv ved hjælp af tabeller, regneudtryk og grafer, hvad en is med $1, 2, 3, 4, …$ kugler koster hos Vaflen og hos Gammeldaws.

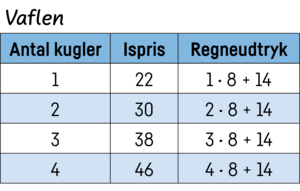
Klassen arbejder med at udfylde tabeller, der viser, hvor meget isvafler med forskellige antal kugler koster hos én af kioskerne, her Vaflen (se Figur 5). Eleverne vil formodentlig regne sig frem til prisen for én kugle og to kugler. Dernæst kan man forestille sig, at nogle elever ud fra disse erfaringer kan argumentere for, at man skal lægge $8$ kr. til for at få $1$ kugle mere. Her fokuserer eleverne på, hvordan de to variable udvikler sig sammen (samvariation): Når der lægges $1$ kugle mere i vaflen, så vokser dens pris med $8$ kr. På den måde kan eleverne udfylde tabellen kugle for kugle.

Læreren kan også spørge til, hvordan eleverne har regnet prisen ud. Nogle elever vil formodentlig fortælle, at de har ganget antal kugler med prisen per kugle og lagt prisen for en vaffel til, og læreren kan skrive deres regneudtryk op i en tredje kolonne i tabellen som i Figur 5. På den måde kan læreren støtte eleverne i at tænke i en korrespondancesammenhæng. Det er vigtigt, at læreren støtter både denne sammenhæng og samvariation.

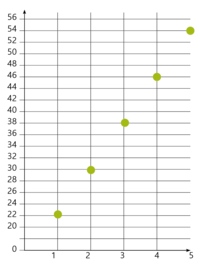
Ud fra tabellen kan eleverne tegne en punktgraf for sammenhængen mellem pris og antal kugler – enten i hånden eller i et Dynamisk Geometri System (se Figur 6) – og sammenligne grafen med tallene i tabellen. Dernæst kan eleverne gøre det samme for køb af is hos Gammeldaws.

I fase 1 er der fokus på at skabe sammenhæng for eleverne mellem de fire typer af repræsentationer: sproglige beskrivelser, tabeller, regneudtryk og grafer.

I fase 2 oversætter klassen deres regneudtryk fra fase 1 til en forskrift for en lineær funktion. Hvis klassen ikke tidligere har arbejdet med sådanne oversættelser, er der brug for, at læreren støtter og forklarer. Udgangspunktet er en samling af elevernes regneudtryk, fx som i Figur 5. Klassen taler om, hvilke mønstre de ser i regneudtrykkene, hvad det er, man regner ud, og hvordan mønstret fortsætter. På den baggrund kan læreren introducere en beskrivelse af sammenhængen som $v(x) = x\cdot 8 + 14$, hvor $x$ er antal kugler, og $v(x)$ er prisen for en is hos Vaflen. Det er vigtigt, at klassen taler om, hvad $x$ og $v(x)$ står for, hvad $v(2)$ betyder, hvad $8$ og $14$ står for, og hvordan forskriften ville se ud med andre priser for en kugle is og for en vaffel. Eleverne kan dernæst selv finde forskriften for den anden iskiosk Gammeldaws, som passende kan kaldes $g(x)$.

Notationen $v(x)$ og $g(x)$ introduceres i denne fase for at navngive funktionerne, så eleverne kan adskille dem fra hinanden. Andre navne kan selvfølgelig også vælges, og læreren kan bruge lejligheden til at tale om navngivning af funktioner og variable mere generelt. Det er dog vigtigt, at læreren fremhæver, at funktionen afhænger af x, og at læreren taler med klassen om, hvordan $v(1)$, $v(2)$, $v(3)$ osv. skal forstås.  

Det er vigtigt, at læreren skaber koblinger mellem forskriften og de andre repræsentationer – tabel og graf – som eleverne brugte i fase 1. Læreren kan fx spørge klassen til betydningen af $8$ og $14$: Hvor kan I se $8$ på grafen? Og $14$? Hvor finder vi $8$ og $14$ i tabellen?

Som afslutning på fase 2 producerer eleverne en plakat, hvor de beskriver de forskrifter, som de er kommet frem til i fase 2. Disse plakater danner udgangspunkt for klassens arbejde i fase 4.   

I fase 3 sammenligner klassen de lineære sammenhænge, som de har arbejdet med i faserne 1 og 2, ved hjælp af tabeller, grafer, forskrifter og ligninger. Fokus er på at sammenligne ved at løse ligninger grafisk og algebraisk, og eleverne kan danne mening hermed, hvis de arbejder med funktionssituationer, som de kender og tidligere har arbejdet med grafisk, fx Isvafler.  

Her arbejder klassen med at finde ud af, hvor mange kugler man skal købe, for at isen koster det samme hos Vaflen og Gammeldaws. Klassen kan løse problemet ved at bruge repræsentationerne fra faserne 1 og 2 (tabeller, grafer, forskrifter og ligninger), men fokus bør være på grafiske og algebraiske løsninger. Mange elever vil sikkert lave to tabeller, dernæst tegne punktgraferne for de to lineære sammenhænge og se, at hvis man køber 3 kugler is, så koster vaflen 38 kr. i begge kiosker. Denne grafiske løsning svarer til at finde skæringspunkter mellem de to grafer (se Figur 7). Andre elever bruger måske kun tabellerne (se Figur 8). Læreren kan tale med klassen om fordele og ulemper ved at bruge tabellen og punktgrafer og fremhæve den grafiske løsning, da graferne giver et bedre overblik over de to sammenhænge, når man køber mange kugler is.

Ud fra den grafiske løsning kan læreren introducere den algebraiske løsning, hvis ingen af eleverne foreslår det. Antal kugler i skæringspunktet kan findes ved at sætte forskrifterne for de to lineære sammenhænge lig med hinanden $v(x)=g(x)$ og løse ligningen $8x + 14 = 10x + 8$. Klassen forventes at have erfaringer med at løse sådanne ligninger (se fx læringssporet ”At løse ligninger”), og læreren kan fokusere på at støtte eleverne i at skabe forbindelse mellem grafen og ligningen. Det er vigtigt, at klassen får mulighed for at skabe sådanne forbindelser i situationer, hvor løsningen af ligningen ikke tager al deres opmærksomhed.

Første gang læreren og klassen gennemløber faserne 1-3, kan det være en god idé at bruge en funktionssituation, som klassen tidligere har arbejdet med, fx sammenhængen mellem antal borde og stole (se læringssporet ”At finde sammenhænge mellem tal”), eller en funktionssituation, som ikke er for svær, fx Isvafler. Når klassen efterfølgende starter med fase 1-3 igen, er det vigtigt, at sværhedsgraden af funktionssituationerne øges. Desuden kan digitale værktøjer, såsom Dynamiske Geometri Systemer og regneark, inddrages mere og mere i konstruktionen af grafer og grafiske løsninger. I de første gennemløb af faserne 1-3 er det dog vigtigt, at klassen tegner grafer og finder grafiske løsninger med papir og blyant. 

I fase 4 tages udgangspunkt i de plakater, som klassen har produceret efter hvert gennemløb af fase 2. Plakaterne beskriver konkrete forskrifter for forskellige lineære funktioner, hvor parametrene a og b varierer – fra positive heltal over negative tal til rationale tal. Idéen er, at klassen via gennemløbene af faserne 1-3 har udviklet så robuste forståelser af funktionsbegrebet og af de forskellige måder at repræsentere funktioner, at de med lærerens støtte kan generalisere de konkrete forskrifter til standardformen for en lineær funktion, $f(x) = a\cdot x + b$ (se Figur 9). 

Læreren kan støtte eleverne ved at tale med klassen om, hvilke mønstre de ser i samlingen af konkrete funktionsforskrifter, hvad der går igen, og hvad der er forskelligt (se Figur 9 for Isvafler). Læreren kan introducere den generelle forskrift og tale med eleverne om sammenhængen mellem den og de konkrete funktionsforskrifter, og hvad parametrene står for.

Dernæst kan klassen undersøge egenskaber ved lineære funktioner ud fra den generelle forskrift. De kan undersøge betydningen af a og b for grafens udseende, hvad $f(0)$ og $f(1)$ er, og hvor de kan aflæses på grafen. Her kan et Dynamisk Geometri System være en god hjælp. Eleverne kan også undersøge parallelle lineære funktioner, såsom $f(x) = 3x + b$, og se på konstante funktioner, $f(x) = b$. 

Når klassen er færdige med dette læringsspor, kan de oplagt arbejde videre med:

• at modellere omverdensproblemer ved hjælp af lineære funktioner og andre funktioner. Det kan være problemer relateret til energiforbrug i hjemmet eller i samfundet.
• andre former for vækst end den lineære, såsom eksponentiel vækst, og med en højere grad af inddragelse af digitale værktøjer.