At løse ligninger
Introduktion
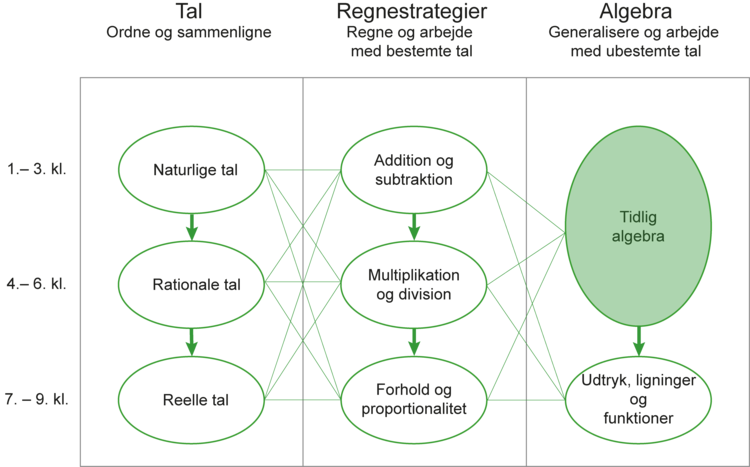
Dette læringsspor sigter mod, at elever udvikler strategier til at løse lineære ligninger. Læringssporet kan begynde i 3. klasse, og det strækker sig over 2-3 år. Set i forhold til stofområdet ’Tal og algebra’ i grundskolen vedrører sporet tidlig algebra (som vist i Figur 1).
Læringsspor til grundskolen udviklet af NCUM under den fælles indsats for tal og algebra.
Udgivet 2025
Forfattere på læringssporet er Charlotte Krog Skott, Morten Blomhøj, Thomas Kaas og Marit Hvalsøe Schou.
En strategi til at løse ligninger er den måde, man håndterer tallene og de ubekendte på for at finde en løsning (inspireret af Hickendorff et al., 2019).
Mål
Læringssporet har to overordnede mål, der hænger sammen:
- Sporet skal bidrage til, at elever udvikler forståelse for egenskaber ved ligninger.
- Sporet skal gøre elever i stand til at opstille og løse ligninger på formen $ax+b=cx+d$, hvor $a,b,c$ og $d$ er heltal, og $x$ er et naturligt tal.
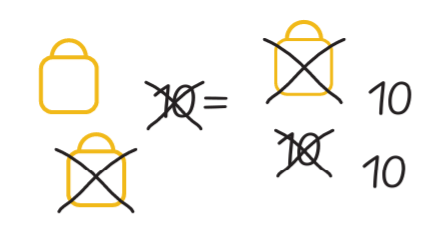
Elever, der i 3. klasse er kommet langt i forhold til det første mål, ved bl.a., at et udtryk som $8 + 4 = \_\_ + 5$ betyder, at værdien af hver side af lighedstegnet skal være den samme. Disse elever kan fx se, at den ukendte værdi må være $1$ mindre end $8$, fordi $5$ er $1$ større end $4$. Elever, der i 5. klasse er kommet langt i forhold til det første mål, ved, at det at løse en ligning som $21-x = 19 + x$ betyder at finde værdier af $x$, som gør, at udtrykkene på hver side af lighedstegnet har samme værdi. En elev kan fx sammenligne udtrykkene og tænke ”Der er $2$ imellem $19$ og $21$, så det må være halvdelen af $2$”.
Elever, der i 3. klasse er kommet langt i forhold til det andet mål, kan løse ligninger, der er knyttet til ligningssituationer og er repræsenteret som tegninger. En elev kan fx tegne eksemplet med Sofus og Alma og tænke ”Jeg ser bort fra én pose og $10$ karameller ved Sofus og ved Alma. Så er der $20$ karameller i en pose”. Elever, der i 5. klasse er kommet langt i forhold til det andet mål, kan løse ligninger skrevet som algebraiske udtryk, fx $18 - 8x = 12x - 2$. En elev kan tænke ”Jeg lægger $8x$ til begge sider. Så $2$ til begge sider. Så er $20 = 20x$, og $x$ er $1$”. En anden elev kan sammenligne de to udtryk og se, at de begge giver $10$, hvis $x$ er $1$.
De to mål understøtter hinanden og udvikles bedst i sammenspil. Således udvikler elever bedre forståelse for egenskaber ved de begreber, som er involveret i ligningsløsning, fx ligheder, ubekendte og variable, når de samtidig udvikler strategier til at løse ligninger.
En ligningssituation er en fortælling eller gåde, der rummer en ligning, som elever kan forestille sig og leve sig ind i. Situationerne er ofte opdigtede og kan derfor virke lidt pseudoagtige sammenlignet med hverdagsproblemer.
Eksempel på ligningssituation:
Sofus og Alma har samlet lige mange karameller til sidste skoledag. De lægger det samme antal karameller i 3 papirposer. Sofus tager 2 poser og har desuden 10 karameller, mens Alma tager 1 pose og har 30 karameller mere. De spørger klassen, om de kan finde ud af, hvor mange karameller der er i hver pose?