Praksis – At løse ligninger
De tidsmæssige rammer
Læringssporet kan startes op i 3. eller 4. klasse, og det anbefales at strække læringssporet over 2-3 undervisningsforløb af 1-3 ugers varighed:
- Opstart i 3. klasse og afslutning i 5. klasse. Fase 1 og 2 kan fx afvikles i samme forløb i 3. klasse, fase 3 i 4. klasse og fase 4 i 5. klasse.
- Opstart i 4. klasse og afslutning i 5. eller 6. klasse. Fase 1 og 2 kan fx afvikles i samme forløb i 4. klasse og fase 3 og 4 i samme forløb i 5. klasse. Alternativt kan fase 4 afvikles i 6. klasse.
De ligninger, der foreslås, svarer til start i 3. klasse. Hvis starten rykkes til 4. klasse, skal tallene tilpasses eleverne, men på en sådan måde at beregninger ikke overskygger deres begrebsforståelse og udvikling af strategier. Men uanset start af læringssporet skal læreren være opmærksom på at tilpasse de foreslåede ligninger til eleverne. Det er også en god idé, at læreren formulerer ligningssituationerne på måder, så rækkefølgen af ubekendte og tal byttes rundt, så klassen kan udvikle fleksibilitet i brug af dem.
Det faglige udgangspunkt
Læringssporet bygger videre på elevernes erfaringer med de naturlige tal og regning fra tidligere undervisning. Læringssporet forudsætter, at eleverne har to typer erfaringer med tal.
Den første forudsætning er, at klassen har erfaringer med de fire regningsarter. Det er en fordel, hvis klassen kender til modsatte regningsarter og ved, at subtraktion er den modsatte regningsart til addition, fx at $22 - 7 = 15$, fordi $15 + 7 = 22$. I fase 3 og 4 er det en forudsætning, at klassen ved, at division er den modsatte regningsart til multiplikation. Afhængig af hvornår læringssporet påbegyndes, vil det variere, hvor store tal klassen skal kunne regne med. Dette gælder også for den anden forudsætning.
Den anden forudsætning er, at klassen har erfaringer med at sammenligne og begrunde, hvorfor nogle regneudtryk har samme værdi. Det er fx vigtigt, at eleverne kan forstå og danne mening med udtryk såsom $10 + 1 = 9 + 2$, $15 + 8 = 13 + 10$, $25 = 17 + 8$, $7 = 7$ og $15 - 22 + 37 = 37 + 15 - 22$.
Fase 1
I fase 1 arbejder klassen med at modellere og løse ligninger, der er beskrevet som ligningssituationer. Ved at gengive situationerne med konkrete materialer, fx poser og karameller eller lign. (se Tilgang), kan klassen repræsentere ligningerne fysisk og løse dem ved at gøre noget med materialerne, såsom at tælle, samle dem i bunker og flytte dem. Det kan støtte eleverne i at udvikle uformelle strategier, der giver mening for dem i forhold til situationerne, og som bygger på deres tidligere erfaringer med tal og regning.
I starten af fase 1 arbejder klassen med ligningssituationer, der er knyttet til ligninger på formen $ax + b = c$, hvor $a$, $b$ og $c$ er naturlige tal. Eksemplet illustrerer, hvordan læreren kan introducere klassen til dette arbejde.
Fase 1
At løse ligninger, der har form som ligningssituationer, ved at bruge uformelle strategier og med støtte i konkrete materialer.
Introduktion af ligninger som ligningssituationer
Læreren kan starte med en ligningssituation i stil med denne:
Kates mor laver en gåde til Kate og hendes veninde Maja: ”I får lige meget slik. Maja, du får 7 stykker. Kate, du får 3 stykker og denne pose med slik i. Hvor mange stykker slik har jeg puttet i Kates pose?”
Den første gang, klassen arbejder med ligninger og ligningsløsning, kan læreren med fordel medbringe rigtigt slik og en pose med det korrekte antal slikstykker i og bruge det til at introducere problemet. Læreren kan iscenesætte situationen ved at lægge Majas $7$ stykker slik på et bord (eller på et stykke papir) og Kates $3$ stykker og pose på et andet bord (eller på et andet stykke papir) og spørge til, hvor mange stykker slik der er i posen. Efter klassen har arbejdet med at løse ligningen og kommet med deres bud på et svar, kan posen åbnes for at tjekke, hvilket svar der er korrekt.
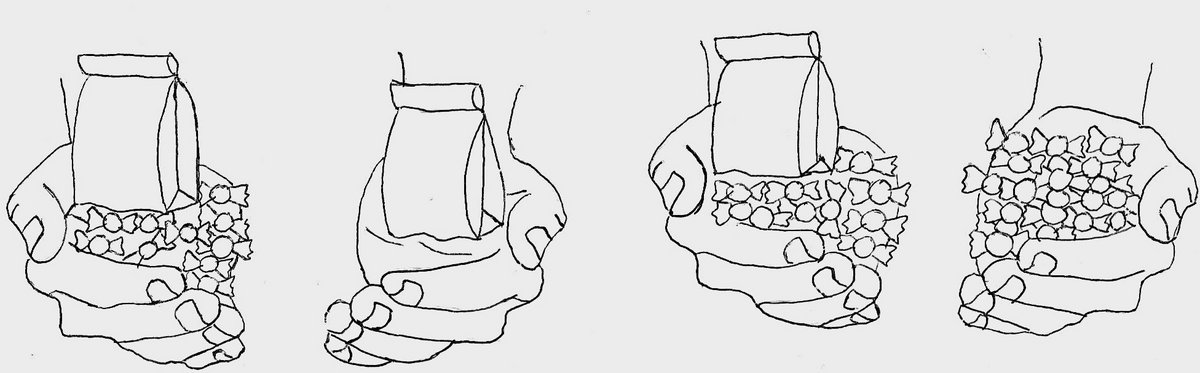
Når eleverne, fx i makkerpar, løser sådanne problemer, er det en fordel, hvis hvert par kan bruge de konkrete materialer, her poser og slik (eller centicubes). Det er vigtigt, at eleverne viser og forklarer deres strategier til klassen, så de kan møde forskellige uformelle tilgange til ligningsløsning og udvikle nye idéer til løsninger. Et par kan fx have brugt en gæt og tjek-strategi til at løse slikproblemet: ”Jeg tænkte, der var $1$ stykke i den. Men det var for lidt. Så prøvede jeg med $2$, så med $3$ og så med $4$, og det passede”. En anden elev kan have beregnet: ”$3$ plus $4$ er $7$, så der er $4$ stykker i”. Et tredje par kan have sammenlignet Kate og Majas slikmængder: ”Kate har $3$ stykker slik. Det har Maja også. Så dem flytter vi her over. Så er der $4$ i posen” (se Figur 5). Klassen kan arbejde videre med sværere ligningssituationer, indtil de fleste er fortrolige med at modellere og løse denne type ligninger med konkrete materialer.

Senere i fase 1 skal klassen arbejde med ligningssituationer, hvor den ubekendte i den tilhørende ligning optræder på begge sider af lighedstegnet og gør det netop én gang mere på den ene side end på den anden. Sådanne situationer er mere udfordrende. Eksemplet viser, hvordan læreren kan introducere sådanne situationer og støtte klassens udvikling af en sammenlign-strategi.
Udvikling af sammenlign-strategi
Læreren kan fx starte med situationen med Sofus og Almas karameller fra Oversigten:
Sofus og Alma har samlet lige mange karameller til sidste skoledag. De lægger det samme antal karameller i 3 papirposer. Sofus tager 2 poser og har desuden 10 karameller mere, mens Alma tager 1 pose og har 30 karameller mere. De spørger klassen, om de kan finde ud af, hvor mange karameller der er i hver pose?
Dette problem er mere udfordrende, fordi både Sofus og Alma har et ukendt antal karameller som en del af de karameller, de har samlet. Læreren kan introducere problemet som i eksemplet Introduktion af ligninger som ligningssituationer ovenfor eller lade to elever spille situationen. Den ene elev har $2$ poser og $10$ karameller (evt. centicubes), mens den anden elev har $1$ pose og $30$ karameller (se Figur 6). De andre elever gætter på, hvor mange karameller der er i en pose, inden de selv i makkerpar skal finde ud af det med de samme konkrete materialer.
Efter et gruppearbejde kan læreren udvælge elever til at forklare, hvordan de løste ligningen. Et makkerpar kan fx have gættet og tjekket: ”Først tænkte vi, at der var $10$ i. Så havde Sofus $30$ og Alma $40$. Ikke rigtigt. Så prøvede vi med $20$. Og det passede”. Eleverne peger på poserne, mens de forklarer. Et andet makkerpar, Ea og Knud, har sammenlignet, hvor mange karameller de har hver især. Knud spiller Alma, og Ea spiller Sofus, og de har taget en pose og $10$ karameller i én af deres egne hænder. Knud siger: ”Så, disse [løfter de $20$ karameller i sin anden hånd] må være lig med denne [peger på posen i Eas anden hånd]” (se Figur 7). Hvis ingen elever sammenligner de karameller, Sofus og Alma har, må læreren bringe en sammenlign-strategi på banen, fx ved at bede klassen om at sammenligne Sofus og Almas karameller og at tænke over, om man kan se bort fra noget, så problemet bliver nemmere at løse.
To pointer kan være vigtige for læreren at fremhæve. Den første pointe knytter sig til Ea og Knuds sammenligning-strategi – eller en anden sammenlign-strategi – og det, at der ses bort fra noget. Pointen kan formuleres i stil med:
Lagde I mærke til, hvad Ea og Knud gjorde? De så først, at både Sofus og Alma har 10 karameller. Ea tog Sofus’ 10 karameller i sin venstre hånd, og Knud tog Almas 10 karameller i sin venstre hånd. De så også, at de begge, altså Sofus og Alma, har en pose med karameller. Ea tog Sofus’ pose i sin venstre hånd sammen med hans 10 karameller, og Knud tog Almas pose i sin venstre hånd sammen med Almas 10 karameller. Så Ea og Knud samler altså det, som både Sofus og Alma har i en af deres hænder, og så ser de bort fra det. Hvorfor mon de gør det? Jeg tror, at de ser bort fra de karameller og poser, som både Sofus og Alma har, fordi problemet så bliver lettere at løse. Nu har Sofus nemlig kun én pose tilbage [peger på Eas anden hånd], og Alma har 20 karameller [peger på Knuds anden hånd]. Så derfor må der være 20 karameller i Sofus’ pose. Kan I se det? I skal nu bruge Ea og Knuds måde at løse problemet på. I skal også tale om, hvorfor man kan se bort fra de karameller og poser, som Sofus og Alma begge har. Og om man altid kan se bort fra noget? Dernæst taler vi sammen om det, og vi ser også, om det er rigtigt, at der er 20 karameller i Sofus’ pose.
Den anden pointe knytter sig til de strategier, som klassen udvikler. Som nævnt i Tilgang er det vigtigt, at eleverne taler om og sammenligner deres strategier. Det er det i forhold til deres udvikling af strategier og deres udvikling af sprog i relation til emnet. En elev kan fx sige: ”Jeg kan altid gætte. Det kan bare tage riiiigtig lang tid at gætte rigtigt. Her var det nu hurtigt nok”. Her får eleven sprogligt formuleret nogle styrker og svagheder ved gæt og tjek-strategien, som det er væsentligt at hele klassen gøres opmærksom på.

Klassen kan arbejde videre med tilsvarende ligningssituationer med støtte i konkrete materialer, indtil de fleste er fortrolige med at bruge en sammenlign-strategi. Det vil sige, at de kan se bort fra det, begge aktører i situationerne har, og forstå, hvorfor man kan gøre det.
Fase 2
I fase 2 arbejder klassen fortsat med ligninger beskrevet som ligningssituationer, men de løser dem med støtte i tegninger. Klassen slipper altså gradvist de konkrete materialer fra fase 1. Hensigten er, at klassen videreudvikler deres uformelle strategier fra fase 1, særligt sammenlign-strategien til fjerne-strategier, som i fase 2 knytter sig til at fjerne ved at subtrahere det samme på begge sider af lighedstegnet.
I starten af fase 2 kan læreren støtte eleverne i at modellere ligningssituationer med tegninger og i at bruge lighedstegnet. Eksemplet viser, hvordan læreren kan gøre det og samtidig støtte klassen i at udvikle deres første fjerne-strategier.
Fase 2
At løse ligninger, der har form som ligningssituationer, ved at bruge fjerne-strategier og med støtte i tegninger.
Klassens første udvikling af fjerne-strategier
Læreren kan tage udgangspunkt i en velkendt ligningssituation for klassen, fx den om Sofus og Alma og deres karameller:
Sofus og Alma har samlet lige mange karameller til sidste skoledag. De lægger det samme antal karameller i 3 papirposer. Sofus tager 2 poser og har desuden 10 karameller mere, mens Alma tager 1 pose og har 30 karameller mere. De spørger klassen, om de kan finde ud af, hvor mange karameller der er i hver pose?
Fremfor at bruge poser og karameller kan læreren introducere problemet ved at skrive Sofus og Alma på tavlen og modellere deres karameller ved at tegne firkanter for poser og skrive 10 for 10 karameller (se Figur 8).
Dernæst kan læreren tegne et lighedstegn mellem Sofus og Almas karameller og spørge klassen: ”Hvad det er for et tegn? Hvad betyder det?”.
Svar fra eleverne, der handler om ”det er et lighedstegn”, ”de er lige store”, ”de er ens” eller ”de har lige mange karameller” er væsentlige at fremhæve og drøfte fælles i klassen.
Eleverne løser først problemet med strategier, de finder på. Dernæst kan læreren digte videre fælles i klassen for at fremskynde fjerne-strategier:
Lærer: Sofus og Alma har en lillebror, som ikke har samlet karameller. Det, synes de, er synd for ham, så de giver ham hver en pose med karameller. De to poser, som de giver til lillebror, visker jeg ud [Figur 9]. Hvor mange karameller har Sofus og Alma hver nu? Før havde de lige mange karameller. Hvad nu?
Knud: De har lige mange. De gav det samme til lillebror.
Lærer: Ok, de har stadig lige mange karameller. Prøv igen at løse problemet. Hvor mange karameller er der i en pose?
Ea: Der er 20.
Lærer: Ok, samme løsning som før. Hvorfor får vi samme løsning? Hov, det var let at løse problemet nu. Hvorfor var det det?
Noa: Fordi der kun var en firkant.
Emilie: Kan man ikke også viske 10 karameller ud?
Lærer: Noa siger, at det var let at løse, fordi der nu kun er én firkant. Sofus og Alma gav hver en pose [peger på firkanterne i Figur 8] til deres lillebror. Vi ved, at der er lige mange karameller i hver af de to poser, så når vi visker dem ud – fjerner dem – så vil Sofus og Alma stadig have lige mange karameller. Men når vi fjerner dem, så bliver problemet lettere at løse.
Så foreslår Emilie, at vi også kan viske 10 karameller ud, altså fjerne dem. Hvad siger I til det?
Det centrale i dialogen er, at klassen ud fra fortællingen i ligningssituationen kan skabe mening med at fjerne noget fra en ligning (her visker de det ud – senere kan de strege det ud for at fastholde løsningsprocessen). Det er således vigtigt, at læreren har fokus på at støtte klassens forståelse af, at det at fjerne det samme er meningsfuldt både ud fra fortællingen og set i forhold til matematikken. Dialogen vil selvfølgelig forløbe anderledes i praksis, så pointen er her at give læreren noget at guide efter i en fælles samtale i klassen; nemlig at skabe denne form for mening med at fjerne det samme på begge sider, og at det bevarer lighed mellem de to sider i ligningen.
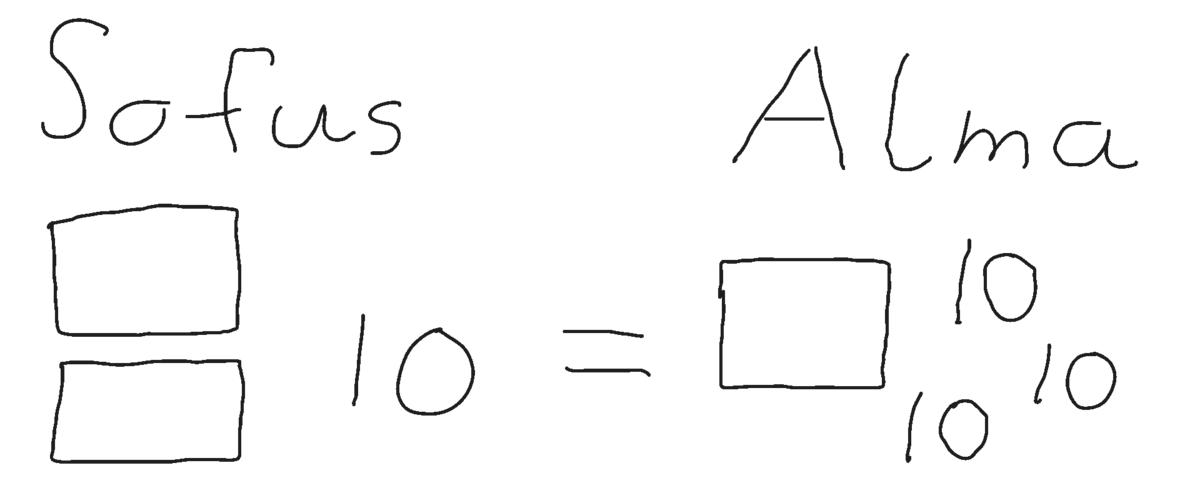
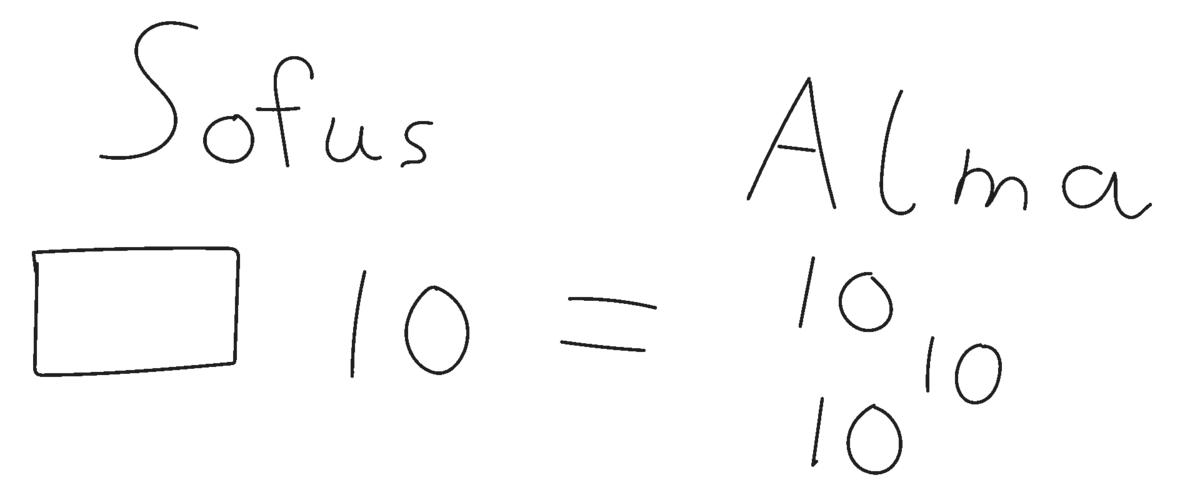
Senere i fase 2 kan læreren støtte klassen i at udvikle deres strategier i retning af metoden fjern og isoler. Disse strategier kan handle om enten at fjerne, indtil eleverne kan løse ligningen, eller om at fjerne, indtil en pose står isoleret på den ene side som i eksemplet med klassens første udvikling af fjerne-strategier. I det følgende eksempel antydes, hvordan læreren kan støtte klassen i at udvikle deres forståelse af at isolere:
Udvikling af klassens forståelse af at isolere
Læreren kan iscenesætte denne ligningssituationen for klassen:
Kristina har 6 hårelastikker, og Sara har 2 hårelastikker. Deres mor laver en gåde til dem: ”Jeg vil give jer pakker med hårelastikker, sådan at I har lige mange elastikker. Hvis jeg giver Kristina 1 pakke og Sara 2 pakker med hårelastikker – og jeg lægger lige mange elastikker i hver pakke – hvor mange hårelastikker skal jeg så lægge i hver pakke?”
Sammen med klassen tegner læreren situationen på tavlen som i Figur 10.
Individuelt eller i makkerpar løser klassen ligningssituationen på tre forskellige måder:
Eksempel 1
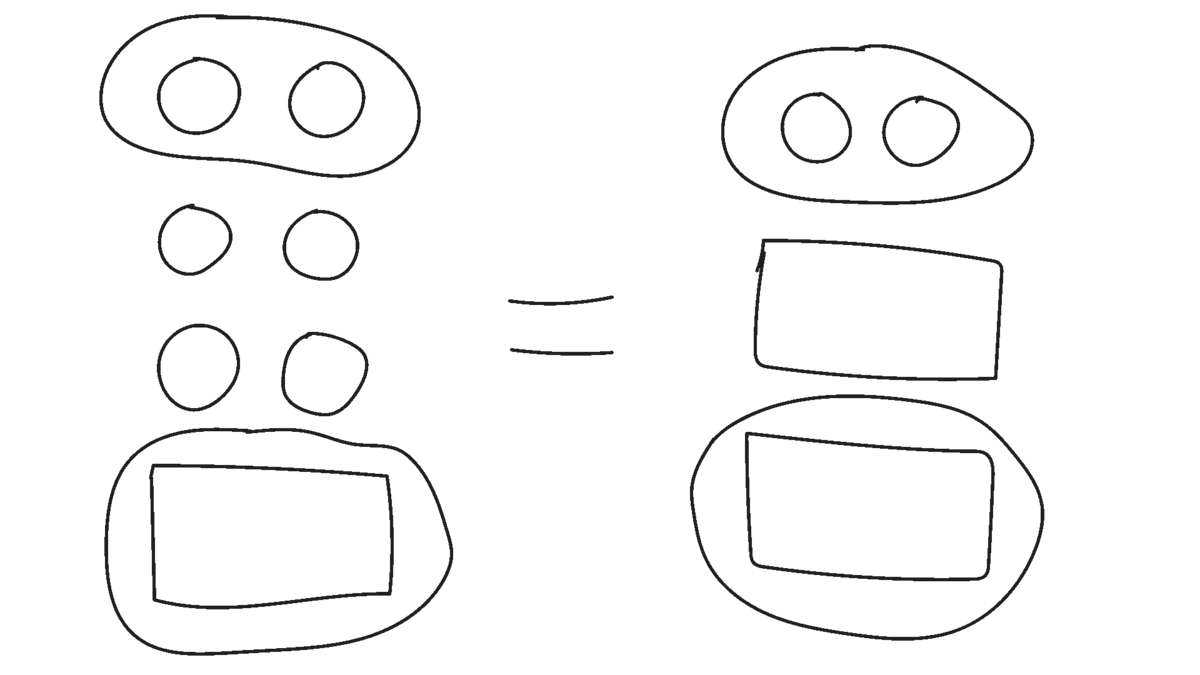
Bo løser situationen ved at sammenligne Kristina og Saras hårelastikker i den tegnede ligning og sætte ring om det, han kan se bort fra, og som er ens (se Figur 11). Bo siger: ”Så er der en firkant her [peger på højre side] og 4 cirkler her [peger på venstre side]”.
Eksempel 2
Lise og hendes makker fjerner ved at viske ud (se Figur 12) og siger: ”Vi viskede to hårelastikker ud. Men vi kunne ikke finde ud af, hvor mange der skulle være i hver firkant. Så tænkte vi, at de gav en firkant væk, og vi viskede dem ud. Så 4”.
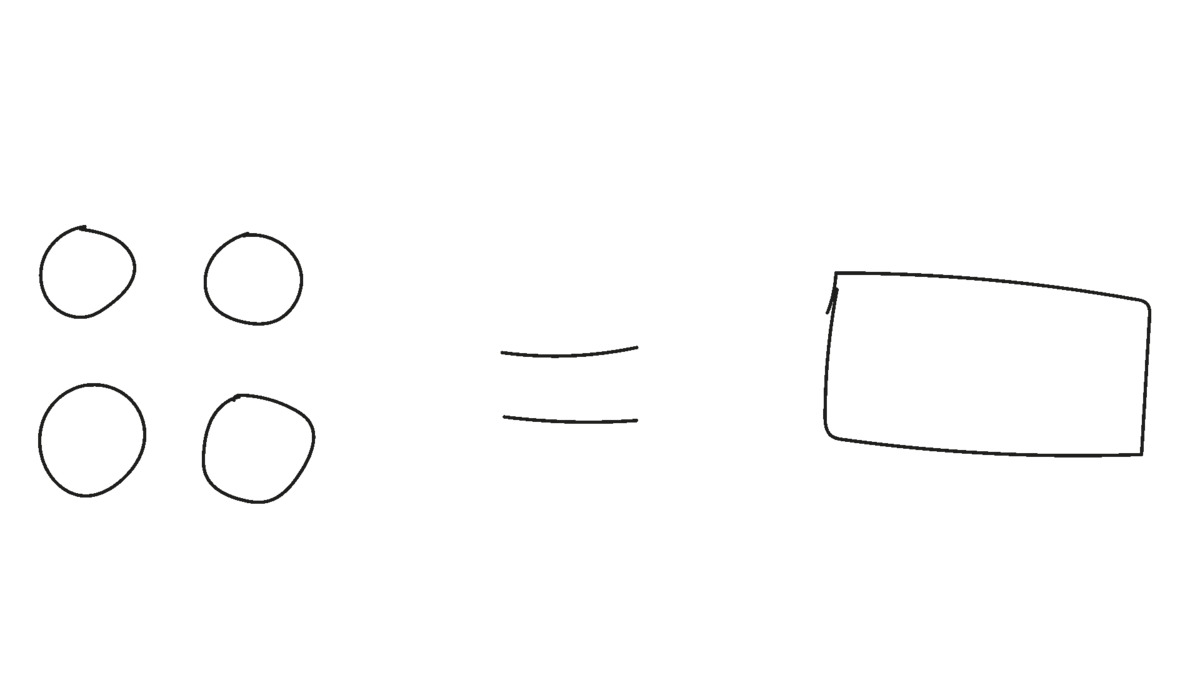
Eksempel 3
Søren og hans makker fjerner som i Figur 13 og siger: ”Vi gad ikke viske ud, så vi stregede bare ud. Og så kunne vi se, at det er 4”.
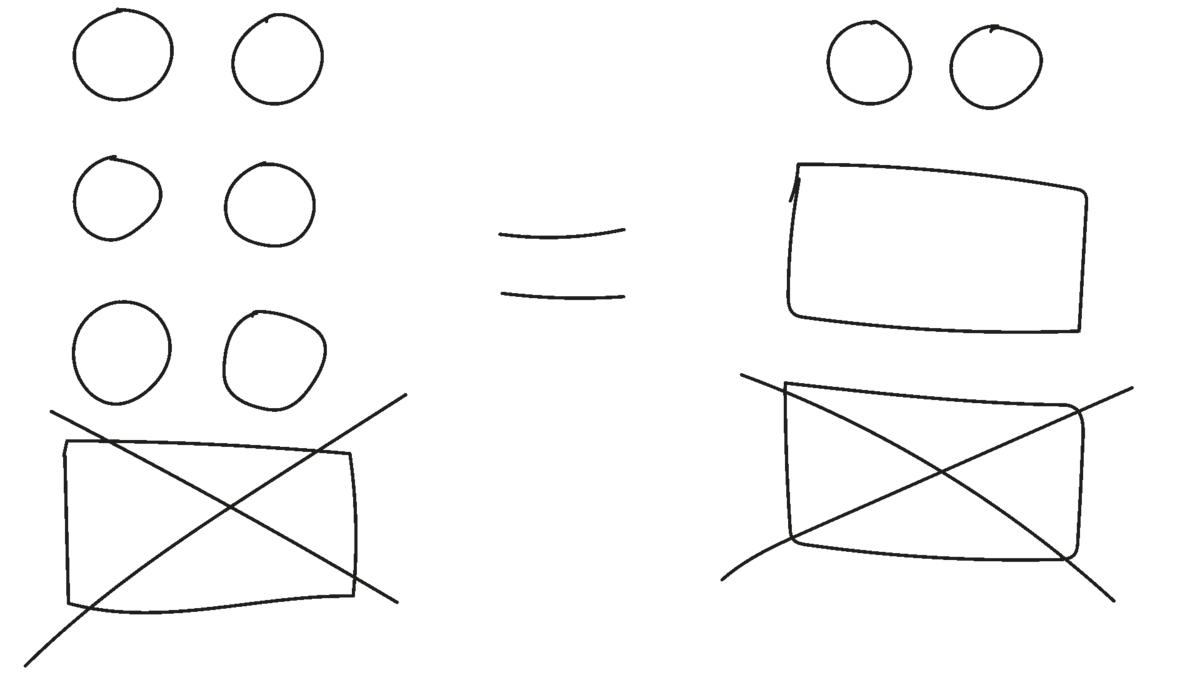
Hvis eleverne foreslår noget i stil med disse tre eksempler, så er der (mindst) to pointer, som læreren kan guide efter. Den første pointe handler om at fjerne det samme på hver side af lighedstegnet, indtil den ubekendte står alene. Pointen kan formuleres i stil med:
Lagde I mærke til, at Bo og Lises gruppe tænkte næsten på samme måde. Bo så på tegningerne på hver side af lighedstegnet og satte ring om det, som både Kristina og Sara har, og som han kunne se bort fra [peger på ringene på Bos tegning]. Lises gruppe så også på begge sider af lighedstegnet, men de viskede det ud, der var ens. Så Bo så bort fra det, der er ens, mens Lises gruppe fjernede det, der var ens [peger på de to tegninger]. Kan I se det? Men det vigtige er, at når Bo og Lises gruppe ser bort fra eller fjerner det samme på begge sider, så kommer pakken til at stå alene på den ene side af lighedstegnet. Og så er det nemt at finde ud af, hvor mange elastikker der er i den. Hvor mange? [4 i kor]. Det er nemt, hvis vi kun behøver at tænke på én pakke på den side af lighedstegnet.
Herefter kan klassen bruge de to strategier på en ny ligningssituation og forsøge at begrunde, hvorfor man kan fjerne det samme på begge sider.
Den anden pointe handler om at fjerne, indtil man kan løse ligningen:
Sørens gruppe gjorde næsten det samme som Lises gruppe. Sørens gruppe fjernede også en pakke fra Kristina og Sara; ikke ved at viske ud, men ved at stege ud. Men de fjernede kun én pakke fra hver side, fordi de så kunne se, at den sidste pakke må indeholde 4 hårelastikker. De kunne altså se eller regne sig frem til, at for at få 6 hårelastikker [peger på venstre siden i Figur 13] så må en pakke indeholde 4 hårelastikker, når der allerede var 2 elastikker i forvejen [peger på højre siden i Figur 13]. Men hvis I ikke lige kan regne jer frem til det i hovedet, så kan I fjerne 2 hårelastikker fra hver side, og så har I løst ligningen på samme måde, som Bo og Lises gruppe.
I stedet for eller i forlængelse af disse to pointer kan læreren vælge at introducere metoden fjern og isoler i tæt tilknytning til klassens forslag. Læreren kan fx foreslå at isolere pakken som antydet i følgende dialog, der er inspireret af en tilsvarende dialog i Radford (2022):
Lærer: Jeg vil gerne, at vi ser bort fra nogle af pakkerne og hårelastikkerne. Det er nemlig nemt, hvis vi kun behøver at tænke på én pakke på den ene side af lighedstegnet. Kan vi nøjes med at tænke på én pakke? Hvordan? Noa?
Noa: Jeg har visket dem ud [peger på en figur i stil med Figur 12].
Lærer: Ok, vent. Lad os viske dem ud én ad gangen. Vi fjerner en elastik [visker en cirkel ud ’under’ Sara], men det [peger på lighedstegnet] siger ’lig med’, at antallet af hårelastikker på begge sider er det samme. Så når du fjerner en elastik fra denne side, hvad skal du så også gøre?
Noa: Viske en elastik ud her [peger på Kristina].
Lærer: Så skal du også fjerne en hårelastik fra denne side [peger på højre side].
Noa: Så kan jeg fjerne en pakke fra Sara og en pakke fra Kristina [visker dem ud] og så…
Lærer: Ja, så du kan også fjerne en pakke fra hver side, for du ved, at der er lige mange hårelastikker i dem. Derfor er antallet af hårelastikker på hver side stadig det samme. Og hvad sker der så? Står pakken alene?
Eleverne: JA!
Noa: Så kan jeg tælle hvor mange elastikker der er… 4.
Lærer: Det betyder, at pakken [peger på Saras firkant] indeholder 4 hårelastikker [peger på Kristinas 4 cirkler].
En introduktion vil formodentlig ikke tage sig sådan ud i praksis, men læreren kan guide efter at give eleverne muligheder for at skabe mening med at isolere pakken og at indse, at løsningen så er let at finde.
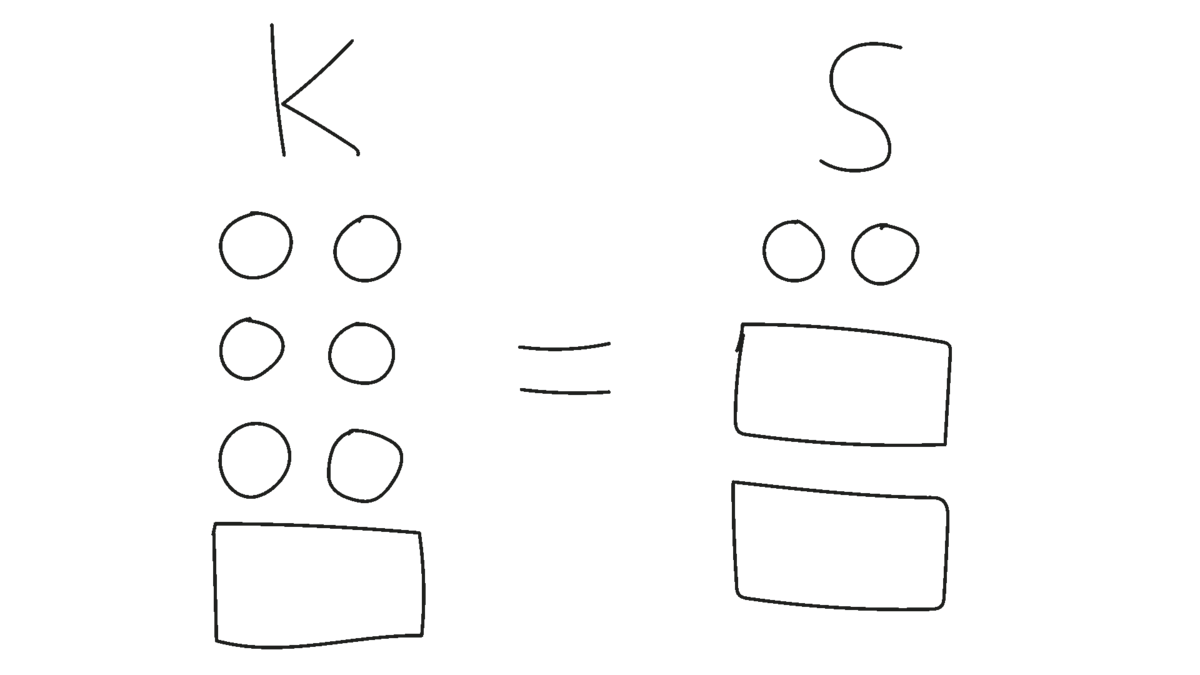
I de opdigtede dialoger i eksemplet har klassen ikke problemer med at se bort fra eller fjerne tegninger af hverken tal eller ubekendte. Læreren skal dog være opmærksom på, at nogle elever kan have svært ved at forstå, at man kan fjerne tegninger af den ubekendte. Disse elever kan have brug for at modellere situationerne med konkrete materialer som i fase 1 (hvor poserne kan indeholde det ukendte antal hårelastikker, slik, mønter eller lign.). Derved kan eleverne erfare, at når de fjerner en pose fra begge sider af lighedstegnet, så fjerner de det samme antal genstande fra hver side, og ligheden bevares derfor. Læreren skal derfor overveje, om enkelte elever bør kunne støtte sig til konkrete materialer, samtidig med at de også tegner.
I fase 2 kan klassen også arbejde med ligningssituationer, hvor de skal fjerne mere end én tegning af den ubekendte og mere end to tegninger af tallene. Det kan fx være ligningssituationer, der svarer til ligningerne $8 + 2x = x + 12$ eller $4x + 7 = 11 + 3x$. Elever kan fjerne én tegning ad gangen og senere flere tegninger (af enten den ubekendte eller tallene) på én gang. Det er vigtigt, at disse regler for at fjerne drøftes i klassen, og at eleverne får mulighed for at formulere og forklare dem med støtte i tegninger af løsninger. For at undgå at skulle fjerne ved at dividere med det samme på begge sider (det er centralt i fase 3) er det vigtigt, at den ubekendte kun optræder én gang mere på den ene end på den anden side af lighedstegnet.
Fase 3
I fase 3 arbejder klassen mest med ligninger skrevet som algebraiske udtryk og løser dem med støtte i tegninger og algebraisk notation (evt. konkrete materialer, hvis enkelte elever har behov). Skiftet fra at arbejde med ligninger som ligningssituationer i fase 2 til at arbejde med dem som algebraiske udtryk skal ske gradvist og i tæt tilknytning til ligningssituationer, der er kendte for eleverne, så de kan skabe mening med den nye notation. Udover at udvikle algebraisk notation er sigtet også, at klassen udvikler deres fjerne-strategier fra fase 2, sådan at de også kan fjerne ved at dividere med det samme på begge sider. Dette er et vigtigt skridt i deres videreudvikling af metoden fjern og isoler.
I starten af fasen kan læreren introducere algebraisk notation. Eksemplet viser, hvordan det kan gøres ud fra en velkendt ligningssituation:
Fase 3
At løse ligninger, der er skrevet som algebraiske udtryk, ved at bruge fjern og isoler-metoden og med støtte i tegninger og algebraisk notation.
Introduktion af algebraisk notation
Læreren tager udgangspunkt i en velkendt ligningssituation for klassen; nemlig den om Kristina og Sara og deres hårelastikker:
Kristina har 6 hårelastikker, og Sara har 2 hårelastikker. Deres mor laver en gåde til dem: ”Jeg vil give jer pakker med hårelastikker, sådan at I har lige mange elastikker. Hvis jeg giver Kristina 1 pakke og Sara 2 pakker med hårelastikker – og jeg lægger lige mange elastikker i hver pakke – hvor mange hårelastikker skal jeg så lægge i hver pakke?”
Dialogen skal antyde, hvordan læreren kan introducere algebraisk notation – særligt bogstavsymboler for den ubekendte:
Lærer: Kan I huske, at vi har arbejdet med en gåde, som handlede om to piger Sara og Kristina og deres hårelastikker? De havde begge nogle hårelastikker, og så fik de nogle pakker med elastikker, som deres mor havde lavet. Når Sara og Kristina lagde elastikkerne i pakkerne fra deres mor sammen med dem, de allerede havde, så havde de lige mange hårelastikker. Jeg har tegnet gåden her [peger på Figur 14]. Gåden var svært at løse, fordi vi vidste, at der var lige mange hårelastikker i hver pakke, men vi vidste ikke, hvor mange der var i én pakke. Det skulle vi finde ud af. Og det gjorde vi ved at tegne pakker og hårelastikker og fjerne nogle af dem. Kan I huske det? Og vi fandt, at der var 4 i hver pakke. Kan I også huske, at det var lidt svært at tegne, og at det tog lidt tid?
Nu vil jeg vise jer, hvordan man kan skrive gåden på matematiksprog. Det er nemlig lidt hurtigere. Jeg skriver $6 + p = 2 \cdot p + 2$ [skriver tal og symboler fortløbende, mens hun siger dem højt (se Figur 15)]. Synes I, det ser lidt mystisk ud? Det forstår jeg. Men prøv lige at snakke med jeres sidemakker om, hvordan det kan give mening? Og hvorfor har jeg skrevet 6 her og p her?
Eleverne kan sige noget med, at ”$p$ er $16$. Når man tæller $a$, $b$, $c$, $d$, …, $p$ [tæller på fingrene samtidig med, at alfabetet siges højt]”, eller ”$p$ er pakke. Du gad bare ikke skrive pakke” eller ”$6$, fordi der er $6$ hårelastikker” eller ”$p$ er elastikker i en pakke”. Pointen her er, at eleverne skal gives mulighed for at skabe mening med den ny notation. De gives sådanne muligheder, hvis notationen knyttes tæt til noget, de allerede kender og forstår, og hvis de kan drøfte meningen med den med hinanden og læreren. I eksemplet er det særligt de to sidste elevsvar, som lærerne bør fremhæve og sætte fokus på i klassens drøftelser.
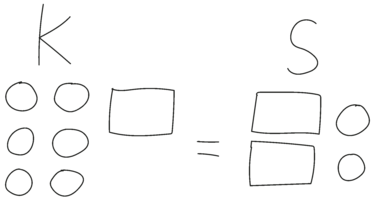
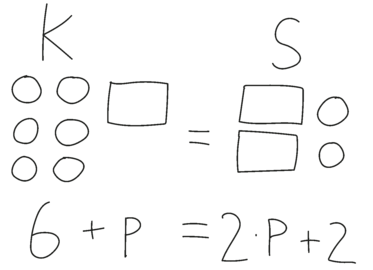
Derefter bruger læreren både tegninger og algebraisk notation til at introducere ligninger, men gradvist skal tegningerne træde i baggrunden. Eleverne løser dog i hele fasen ligningerne i en blanding af tegninger og algebraisk notation (evt. konkrete materialer), og læreren skal i hele fasen støtte dem i udvikle algebraisk notation, bl.a. ved at støtte dem i at skabe sammenhæng mellem notationen og ligningssituationen og drøfte meningen med den algebraiske notation som i eksemplet med introduktion af algebraisk notation ovenfor.
I fasen videreudvikler klassen også fjern og isoler-metoden – specifikt ved at videreudvikle fjerne-strategierne fra fase 2, så klassen også kan fjerne ved at dividere med det samme på begge sider af lighedstegnet. At fjerne ved division er vigtig, særligt når elever skal isolere den ubekendte i ligninger, såsom $2x=12$. Det kan også være hensigtsmæssigt, når elever skal omskrive og reducere ligninger, såsom $14+8x=6x+20$, hvor tallene har samme divisor (her 2).
At fjerne ved at dividere
Når klassen har omskrevet en ligning til $2x = 12$ ved at fjerne og isolere, så skal de kunne isolere $x$ ved at dividere med $2$ på begge sider og på den måde fjerne $2$ fra venstresiden. Det er imidlertid vigtigt, at klassen udvikler denne fjerne-strategi ud fra deres tidligere forståelser og erfaringer. Når klassen skal isolere $x$ – eller få $x$ til at stå alene – i fx $2x = 12$, så vil nogle elever trække på deres forståelse af division som ligedeling og skal derfor have mulighed for at fordele $12$ på $2$ ubekendte, mens andre elever vil tænke i modsatte regningsarter, fx at når $2 \cdot 6 = 12$, så må $x = 6$. De ligninger, som klassen arbejder med, skal give eleverne mulighed for at tænke på sådanne måder og samtidig modsvare klassens faglige niveau. Klassen kan først arbejde med ligninger som $2x=12$, $5x + 3 = 9 + 3x$ og $9x + 8 = 5x + 16$ og senere med ligninger, hvor tallene er større, så det er vanskeligere at isolere $x$ uden at dividere, fx $45 + 15x = 2x + 162$.
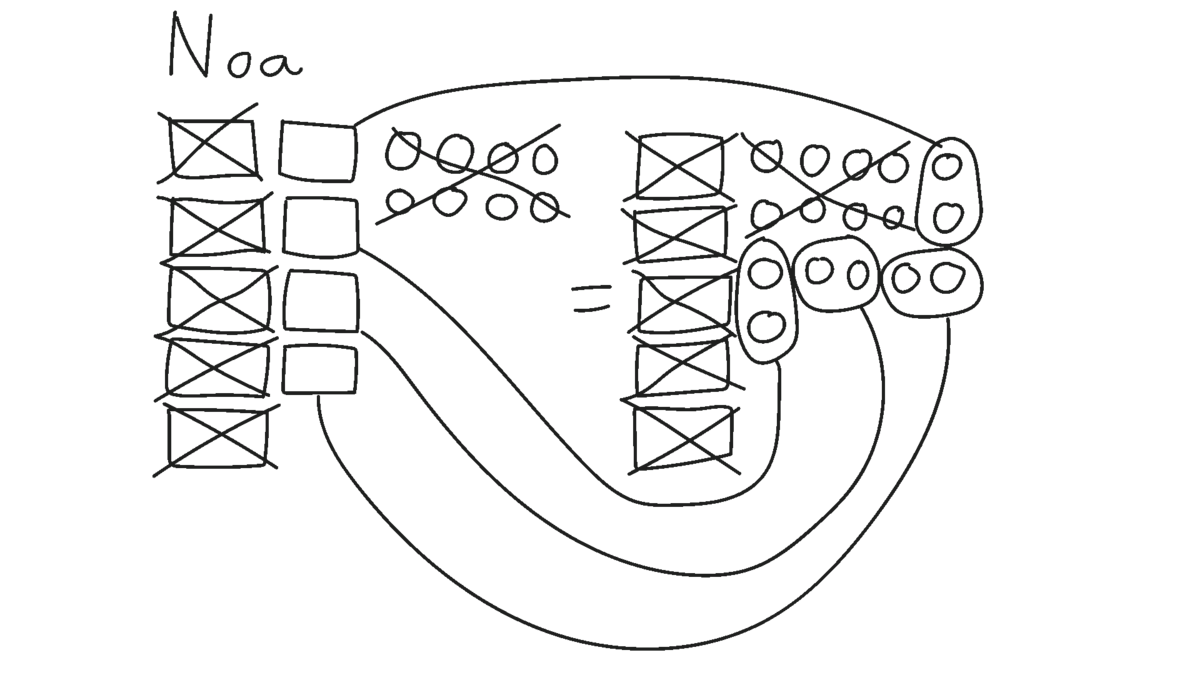
I en klasse har eleverne arbejdet med ligningen $9x + 8 = 5x + 16$. To af eleverne, Noa og Else, har løst den på hver sin måde som vist i Figur 16. Læreren kan sammenligne deres metoder og strategier og støtte klassens udvikling af algebraisk notation og strategier, fx på denne måde:
Lærer: Prøv at se på Noas og Elses løsninger. Hvis I ser godt efter, kan I se, at de har tænkt meget det samme. Men der er også forskelle.
En forskel er, at Else har været mere doven end Noa. Else har ikke gidet tegne alle firkanterne – altså $x$’erne – som Noa har gjort. I stedet har hun skrevet, hvor mange firkanter der er. Else har fx skrevet $9$ firkanter her og $5$ firkanter her [peger på Elses løsning]. Så har hun fjernet disse $5$ firkanter fra denne side og fra den anden – eller det vil sige, at Else har trukket $5$ firkanter fra på begge sider [peger på Elses anden omskrivning]. Noa har også fjernet $5$ firkanter fra hver side ved at strege dem ud [peger på Noas løsning].
Else og Noa prøver altså begge at få firkanterne – altså $x$’erne – til at stå alene på den ene side. Kan I se det? Kan I også se, at de begge fjerner $8$ – eller trækker $8$ fra – på begge sider [peger på Elses anden omskrivning]? De får begge, at $4$ firkanter – eller $4$ x'er – skal indeholde $8$ [peger på deres tegninger].
Her støtter læreren klassen i at udvikle deres måder at skrive ligninger på som algebraiske udtryk. Læreren fremhæver fx det tidsbesparende i at skrive antallet af firkanter frem for at tegne hver af dem og knytte firkanter til den ubekendte $x$. Læreren støtter også elevernes udvikling af at fjerne og isolere ved at fremhæve, at både Noa og Else forsøger at få tallene til at stå på den ene side af lighedstegnet og den ubekendte på den anden. Endelig støtter læreren som noget centralt elevernes videreudvikling af fjerne-strategier ved at beskrive det at fjerne som at trække fra. Dette skifte fra at fjerne til at trække fra er vigtigt, når ligninger har form som algebraiske udtryk. Det giver nemlig ikke matematisk mening ’at fjerne’ noget i et algebraisk udtryk – her benyttes regnearterne til at fjerne i overensstemmelse med reglerne for ligningsløsning (se Tilgang).
Med henblik på at støtte klassens videreudvikling af fjern og isoler-metoden og fjerne-strategier i relation til division kan læreren fortsætte:
Lærer: Nu bliver det spændende at se, hvad Noa og Else så gør. For det er nyt for os – vi plejer jo at få én firkant eller ét $x$ til at stå alene. Men nu har Noa og Else fået $4$ firkanter eller $4$ $x$'er til at stå alene. Noa har tegnet de $4$ firkanter, og han kan se, at hvis han samler cirklerne to og to, så kan hvert par være i en firkant [peger på Noas tegning]. Kan I se det? Else gør noget lidt andet. Hun får, at $4$ firkanter er lig med $8$. Hun kan så se, at én firkant, ét $x$, indeholder $2$, fordi $4 \cdot 2 = 8$, eller fordi $8$ divideret med $4$ er $2$. Både Else og Noa får det samme resultat; nemlig $2$. Det tyder på, at man kan gøre det på begge måder. I skal nu prøve både Noas og Elses måder på en ny ligning, $11x + 3 = x + 23$.
Ved at sammenligne og afprøve de to elevers måder at isolere den ubekendte får klassen mulighed for at udvikle fjerne-strategier i relation til division og kan i den proces trække på deres erfaringer og forståelser fra division med de naturlige tal. Det er vigtigt, at strategierne formuleres i relation til elevernes arbejde, så eleverne kan danne mening med dem.
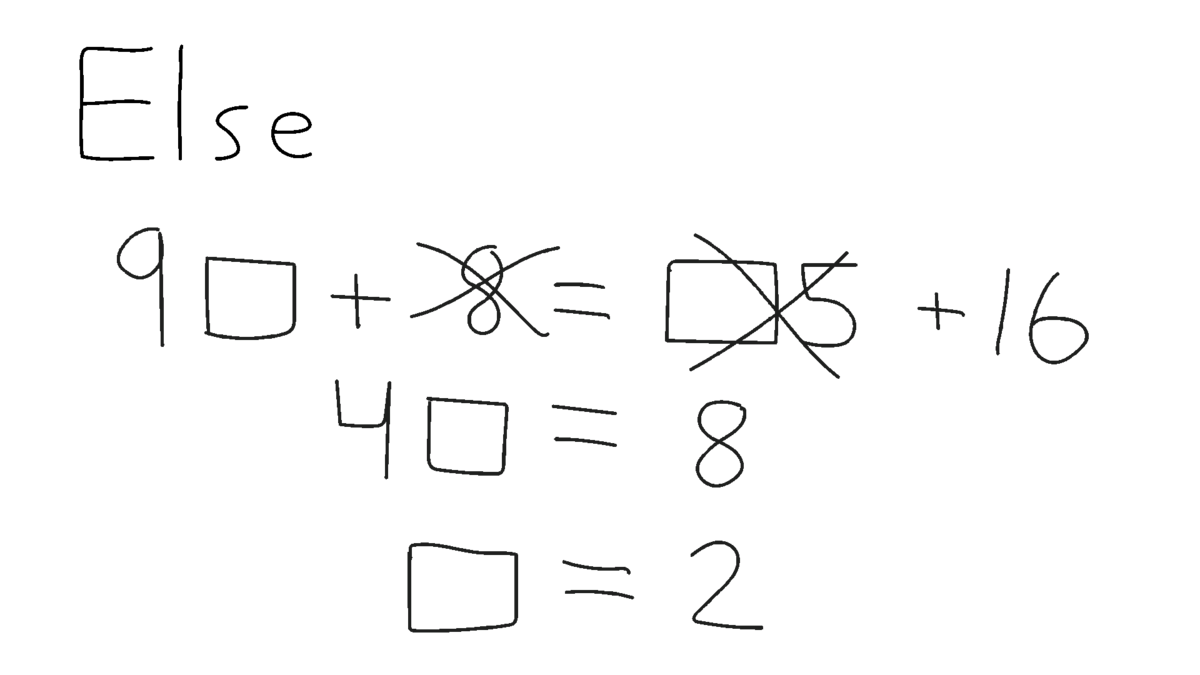
At omskrive ved at dividere
Eleverne kan også udvikle deres fjerne-strategier, når de omskriver og reducerer en ligning ved at dividere med det samme på begge sider. Omskrivning er oplagt, hvis tallene i en ligning har samme divisor – fx går $2$ op i alle tallene i $14 + 8x = 6x + 20$. Læreren kan digte videre på situationen med Sofus og Alma, så Sofus’ karameller svarer til ligningens venstre side. og Almas karameller svarer til dens højre side, og fortælle, at både Sofus og Alma giver halvdelen af deres karameller til deres lillebror. Læreren kan dernæst bede eleverne om at løse begge problemer – både før og efter at Sofus og Alma har foræret deres lillebror halvdelen af deres karameller. Hensigten er, at eleverne kan forstå og skabe mening med, at man dividerer en ligning med 2 ved at dividere hvert led med $2$, så ligningen forenkles til $7 + 4x = 3x + 10$. Løsningen af denne ligning giver samme værdi af den ubekendte som løsningen af den oprindelige ligning. Pointen er, at klassen kan opdage, at rækkefølgen af deres brug af fjerne-strategier – om de først fjerner ved at dividere og dernæst ved at subtrahere eller omvendt – ikke har betydning for resultatet, men at det kan betyde noget for, hvor nem en ligning er at løse.
Fase 4
I fase 4 arbejder klassen med ligninger skrevet som algebraiske udtryk og løser dem med støtte i noter, der kan være en blanding af algebraisk notation og tegninger. Sigtet med fasen er, at klassen bliver stadig mere fortrolig med algebraisk notation, og at de kan løse ligninger, der involverer subtraktion, ved at fjerne og isolere. I fasen udvikler klassen derfor deres fjerne-strategier fra fase 2 og 3 til også at kunne fjerne ved at addere det samme på begge sider – dermed kan de løse ligninger, der involverer subtraktion. Sådanne ligninger er vanskelige at repræsentere med ligningssituationer, konkrete materialer og tegninger, så algebraisk notation bliver påtrængende på en anden måde i denne fase end i de andre tre faser.
I fase 4 arbejder klassen først med ligninger, hvor et tal subtraheres, fx $3x - 5 = 2x + 7$. Eksemplet viser, hvordan læreren kan introducere denne type ligninger.
Fase 4
At løse ligninger, der er skrevet som algebraiske udtryk, ved at bruge fjern og isoler-metoden og med støtte i algebraisk notation.
Introduktion af ligninger med negative tal
Læreren kan introducere ligninger med negative tal, fx $3x-5=2x+7$, som antydet i den opdigtede dialog ved at trække på elevernes tidligere forståelser. Samtidig støtter læreren også eleverne i at løse ligningerne og giver dem dermed mulighed for at udvikle deres fjerne-strategier:
Lærer: Denne ligning er anderledes end dem, vi har arbejdet med før. Det er den, fordi der står her, at 5 skal trækkes fra. Før har der altid stået plus. Prøv at tænke på, hvordan vi tidligere har løst ligninger. Hvad foreslår I, at vi gør?
Malte: Fjerner $7$.
Lærer: Ok, jeg kan godt fjerne eller trække $7$ fra her [peger på $7$ på højre side]. Men jeg skal jo også trække $7$ fra her [peger på venstre side]. Her står, at jeg skal trække $5$ fra, så hvis jeg skal trække $7$ mere fra, så kommer der til at stå, at jeg skal trække $12$ fra. Det kan man godt, men det bliver besværligt. Derfor foreslår jeg, at vi gør noget andet end at trække $7$ fra på begge sider. Ja, Sofie?
Sofie: Kan vi trække $2x$ fra begge steder?
Lærer: Lad os prøve det. Jeg skriver "Trækker $2x$ fra" til venstre, så vi kan se, hvad vi gør. Hvad får jeg, hvis jeg trækker $2x$ fra venstresiden? (se Figur 17)
Malte: $x-5$
Lærer: $x-5$. Og når jeg trækker $2x$ fra højre side?
Ali: Det forsvinder, så kun $7$.
Lærer: Ok, $2x$ forsvinder. Nu har vi kun ét $x$ på venstre side. Så det var smart at trække $2x$ fra. Hvad kan jeg gøre for at få $x$ til at stå helt alene?
Rahat: Lægge $5$ til.
Lærer: Ok, lad os prøve det. Jeg skriver "Lægger $5$ til", så vi kan se, hvad vi gør. Hvad får jeg, når jeg lægger $5$ til venstresiden? Og til højresiden?
Sofie: Bare $x$ på den ene side og $12$ på den anden. Så $x=12$. Men du ku' osse bare se det. Hvis du skal trække $5$ fra noget, og det skal være $7$, så er det $12$.
Lærer: God pointe. I skal nu sammen med jeres sidemakker løse denne ligning [skriver $6+3x=5x−4$ på tavlen].
Klassen kan stadig bruge en blanding af tegninger og algebraisk notation, når de løser disse ligninger. Dog skal tegningerne suppleres med nye ikoner for at kunne illustrere det at addere med det samme på begge sider, fx ved at tegne en ring omkring det, der adderes, med en til-pil. Læreren skal derfor afveje i fase 4, om det er indsatsen værd at tilføje ikoner til tegninger (som repræsentation), eller om det er bedre at fokusere på algebraisk notation. Læreren i dialogen beskriver omskrivningerne med tekst og algebraisk notation og understøtter dermed klassens forståelse af algebraisk notation. Men det er en balance, der skal afvejes i forhold til klassen samlet set og i forhold til enkeltelever, som kan have behov for at kunne tegne i længere tid for at forstå fjerne-strategierne og de regler, som de bygger på.
Som opfølgning på dialogen kan eleverne og læreren drøfte, hvorfor det er smartere at subtrahere $2x$ på begge sider end at subtrahere $7$. Det er matematisk set korrekt at subtrahere $7$ fra begge sider, da ligheden bevares, men det gør ligningen mere kompleks, da eleverne så skal håndtere negative tal og et negativt antal ubekendte (fx $-12=-x$). Samtidig gør det løsningsprocessen mere besværligt, da eleverne skal addere $12$ og $x$ til begge sider af lighedstegnet. Det er vigtigt, at eleverne taler med hinanden og læreren om, hvordan det er smartest at omskrive en ligning, når de fjerner og isolerer, fx ved at sammenligne deres omskrivninger som i eksemplet nedenfor om, hvad der er smart at fjerne først.
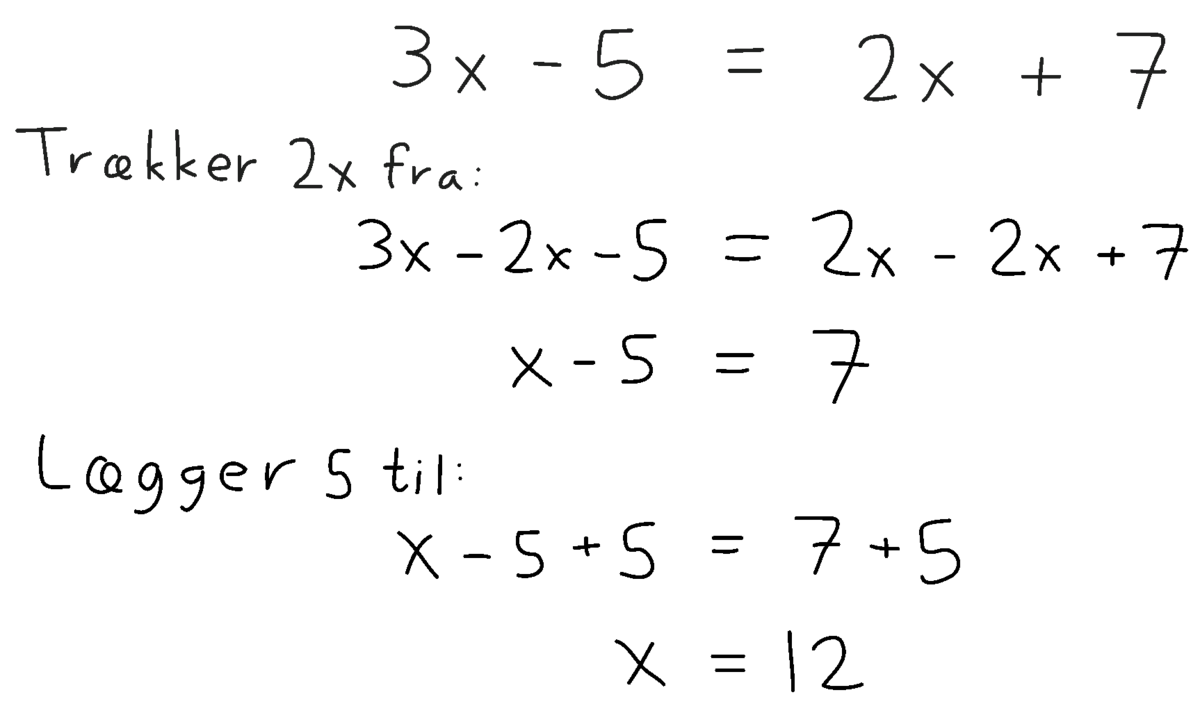
Senere i fase 4 kan klassen arbejde med ligninger, hvor også den ubekendte subtraheres, såsom $5x-4 = 10-2x$. Eksemplet viser, hvordan læreren kan støtte klassen arbejde med at fjerne i sådanne ligninger, og hvad der er smart at fjerne først.
Hvad er smart at fjerne?
Eleverne løser ligningen $5x-4=10-2x$ individuelt eller i makkerpar. Læreren kan opfordre eleverne til at skrive ned, hvordan de fjerner fra den ene omskrivning til den anden – som i dialogen i eksemplet ovenfor med ligninger med negative tal. Dette kan hjælpe eleverne til at se, at man fjerner ved at bruge den modsatte regningsart til det, som man gerne vil fjerne, og at gøre dette på begge sider.
I Figur 18 ses Anton og Livs forslag, der er meget forskellige ift. brug af tegninger og algebraisk notation. Forslagene tyder imidlertid på, at både Anton og Liv forstår og kan bruge fjerne-strategier som en del af fjern og isoler-metoden.
Der er flere pointer i forhold til, hvad der er smart at fjerne først, som læreren kan støtte ved at sammenligne og drøfte disse to eller lignende løsninger med klassen:
-
Støt klassen i at tegne mindre og bruge mere algebraisk notation. Lad evt. klassen skrive Antons løsning, som Liv har gjort, og omvendt, og brug det som udgangspunkt for en samtale om, hvad der er nemmest.
-
Fremhæv, at i ligninger, hvori der indgår subtraktion af et tal eller en ubekendt, kan man fjerne ved at addere det samme på begge sider. Tag evt. udgangspunkt i, at både Anton og Liv fjerner ved at addere $4$ og $2x$, og drøft, hvorfor det er smart.
-
Drøft, hvilke fjerne-strategier der er smartest, fx med udgangspunkt i spørgsmål som: "Hvorfor lægger både Anton og Liv to firkanter/$x$'er til? Hvorfor trækker de ikke fem firkanter/$x$’er fra?". Svar fra eleverne i stil med ”Det gælder om at omskrive så få gange som muligt”, ”Du skal tage det mindste tal eller mindste antal firkanter og så gøre det modsatte” eller ”Du må ikke få tal eller $x$’er, der skal trækkes fra” eller ”Man skal samle tal på en side og $x$’er på den anden side, så de er positive” er værd at fremhæve og drøfte i klassen.
-
Drøft rækkefølgen af Anton og Livs omskrivninger. De har begge fjernet på samme måder, men i forskellig rækkefølge: Hvorfor er det ok? Hvad er smartest at gøre? Er der fjerne-strategier, man bør bruge sidst? Eller først?
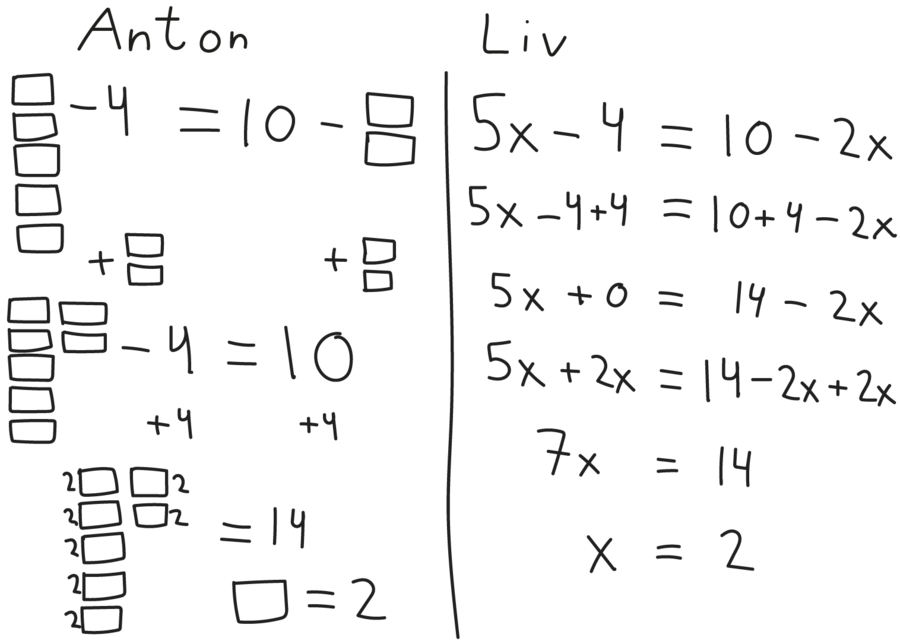
Det er vigtigt, at klassen får mange erfaringer med at arbejde sprogligt – både mundtligt og skriftligt – med ligninger og ligningsløsning som dem i fase 4, og at de bliver fortrolige med at fjerne både ved at subtrahere, dividere og addere og med at fjerne og isolere. En supplerende måde at styrke klassens fortrolighed er, at eleverne selv konstruerer ligninger med bestemte løsninger. De kan fx tage udgangspunkt i, at løsningen skal være $x = 3$ eller lign. (men ikke et negativt tal eller en brøk) og så bruge de tre regler for subtraktion, division og addition, som fjerne-strategierne bygger på, til at omskrive ligningen ’den modsatte vej’. Eleverne kan dernæst udveksle ligninger og løse hinandens og efterfølgende drøfte, om deres løsninger svarer til den måde, som ligningen blev konstrueret. En sådan aktivitet synliggør på en anden måde for klassen de regler for ligningsløsning, som fjerne-strategierne bygger på, og den giver klassen mulighed for yderligere at udvikle deres forståelse af ligninger, fjerne-strategier, fjern og isoler-metoden og algebraisk notation.