Praksis – At sammenligne lineære funktioner
De tidsmæssige rammer
Læringssporet er tænkt til 5 ugers matematikundervisning med start i 7. eller 8. klasse, fx:
- 2 uger i 7. klasse til 2-3 gennemløb af faserne 1-3, og 3 uger i 8. klasse til 2-3 gennemløb af faserne 1-3 og en afrunding med fase 4.
- 3 uger i 8. klasse til 3-4 gennemløb af faserne 1-3, og 2 uger i 9. klasse til 1-2 gennemløb af faserne 1-3 og en afrunding med fase 4 (se Figur 2 under Tilgang).
Der kan være overlap mellem dette læringsspors første to faser og læringssporet ”At finde sammenhænge mellem tal”. Afhængigt af klassens niveau, og hvor meget klassen har arbejdet med dette spor, kan der lægges mindre vægt på de første faser og mere vægt på fase 3 og 4. Eller der kan bruges sværere lineære sammenhænge i faserne 1-3, hvor parametrene er rationelle tal, og variablene er reelle tal.
Det faglige udgangspunkt
Læringssporet bygger videre på to tidligere læringsspor ”At finde sammenhænge mellem tal” og ”At løse ligninger”. Den første forudsætning er derfor, at klassen har erfaringer med at opdage, beskrive og generalisere sammenhænge mellem naturlige tal – såsom arealet af rektangler med en fast sidelængde og sammenhænge mellem to personers aldre – med støtte i sproglige beskrivelser, regneudtryk, tabeller og algebraisk notation. Klassen kan bygge videre på deres tidligere erfaringer og styrke dem i dette læringsspor.
Den anden forudsætning er, at klassen har erfaringer med at opstille og løse lineære ligninger såsom $4x-5=3+2x$. Klassen kan bygge videre på deres tidligere erfaringer og styrke dem i dette læringsspor via dets fokus på grafiske og algebraiske løsninger af ligninger.
Den tredje forudsætning er, at klassen har erfaringer med at bruge Dynamiske Geometri Systemer og regneark, så de kan lave tabeller og tegne grafer ved hjælp af dem og lave simple formler i regneark.
Fase 1
I fase 1 er det hensigten, at klassen får erfaringer med at oversætte lineære sammenhænge, der er beskrevet sprogligt i funktionssituationer, til tabeller, regneudtryk og grafer. Klassen kan med fordel drøfte ligheder og forskelle mellem repræsentationerne, da det kan styrke dem i at kunne skifte fleksibelt mellem repræsentationerne og at vælge hensigtsmæssige repræsentationer i en bestemt situation.
I de tre første faser bruges eksempel 2, Lodsedler, som gennemgående funktionssituation. Lodsedler er valgt, da eksemplet kan siges at være midt i progressionen af funktionssituationer, som klassen kan arbejde med i de 5-6 gennemløb af faserne 1-3, som læringssporet lægger op til. Den uafhængige variabel (antallet af solgte lodsedler) er et naturligt tal, men der kan sælges så mange lodsedler, at punktgrafen næsten bliver en sammenhængende ret linje. Lodsedler kan dermed danne overgang fra punktgrafer til rette linjer, hvor den uafhængige variabel er et reelt tal. Derudover involverer Lodsedler nogle engangsudgifter og dermed subtraktion af parameteren $b$. Eksemplet kan gøres lettere ved at fjerne engangsudgifterne eller udgifterne til organisationen eller klubben. Det kan gøres sværere ved at øge priserne og/eller at bruge decimaltal eller brøker som priser. Læreren må justere situationens sværhedsgrad i forhold til sin klasse eller enkeltelever.
De to eksempler herunder handler om en klasses arbejde med Lodsedler. Det første eksempler viser, hvordan læreren kan støtte klassen i at beskrive sammenhængen mellem antal solgte sedler og det, de tjener, med et regneudtryk. Det andet eksempel viser, hvordan repræsentationerne kan komme i spil på forskellige måder med fokus på at sammenligne dem.
Fase 1
At oversætte sproglige beskrivelser af lineære sammenhænge til tabeller, regneudtryk og grafer.
Tabel med regneudtryk
Læreren kan iscenesætte Lodsedler med fokus på, at eleverne skal bestemme, hvor meget deres klasse kan tjene på én dag (eller en uge) ved at sælge lodsedler for først velgørenhedsorganisationen og senere sportsklubben. Denne iscenesættelse lægger op til, at eleverne formulerer et regneudtryk for sammenhængen mellem antal solgte lodsedler og det, klassen kan tjene. Fokus er derfor primært på korrespondancesammenhæng mellem de to variable.
7. klasse skal tjene penge til deres lejrskole. De kan sælge lodsedler for en velgørenhedsorganisation og få $15$ kr. pr. lodseddel. Heraf skal organisationen have $6$ kr., og klassen vil have udgifter for $90$ kr. Eller de kan sælge lodsedler for en sportsklub, hvor én lodseddel koster $7$ kr., og de får $100$ kr. i opstart til udgifter. Hvor meget kan klassen tjene, hvis de sælger lodsedler for velgørenhedsorganisationen? For sportsklubben?
Eleverne kan med fordel lave et skøn af, hvor mange lodsedler en elev i gennemsnit kan sælge på én dag. Den opdigtede klassesamtale herunder skal illustrere, hvordan læreren kan støtte klassen i at beskrive sammenhængen med et regneudtryk. Læreren samler op på klassens arbejde ved at lave en tabel med deres resultater og fylde nogle af tabellens huller ud sammen med klassen:
Lærer: Lad mig høre, hvad I har fået, og hvordan I er kommet frem til det. Jeg har lavet en tabel her på tavlen, hvor jeg har skrevet ”Antal solgte lodsedler” i den ene kolonne og ”Klassen tjener” i den anden (se Figur 10). Så … ja, Otto?
Otto: Vi tænkte, at vi var supergode til at sælge lodder. Vi sælger $50$ sedler hver. Så bliver det $10.710$ kr.
Lærer: Ok, så hvad skal jeg skrive her under antal solgte sedler?
Otto: Du skal skrive $50$ … gange $24$ … $1000$, nej $1200$ sedler.
Lærer: Ok. Kan en anden fra gruppen forklare, hvordan I er kommet frem til $10.710$ kr.?
Emma: Fordi en seddel koster $15$ kr., og så skal vi give $6$ kr. til dem. Så vi får kun $9$ kr. per seddel. Det gangede vi med $1200$ … og trak $90$ kr. fra.
Lærer: Ok. Jeg laver en ny kolonne her, hvor jeg skriver jeres måde at regne det ud på. Så $9$ gange $1200$ kr. minus $90$ kr. Andre resultater og måder at regne det på?
Sofie: Vi har tænkt, at vi kan sælge $2$ sedler hver. Så det er $48$ sedler. Det giver først $15$ gange $48$, det er $720$, så $6$ gange $48$, nej, det er $288$. Det skal trækkes fra, så det er [kigger i sine noter] $432$ og så $90$ fra det. Det er $342$.
Lærer: $15$ gange … [gentager Sofies forklaring, samtidig med at han skriver $15\cdot 48 - 6\cdot 48 - 90$ på tavlen]. Lad mig få nogle flere bud …
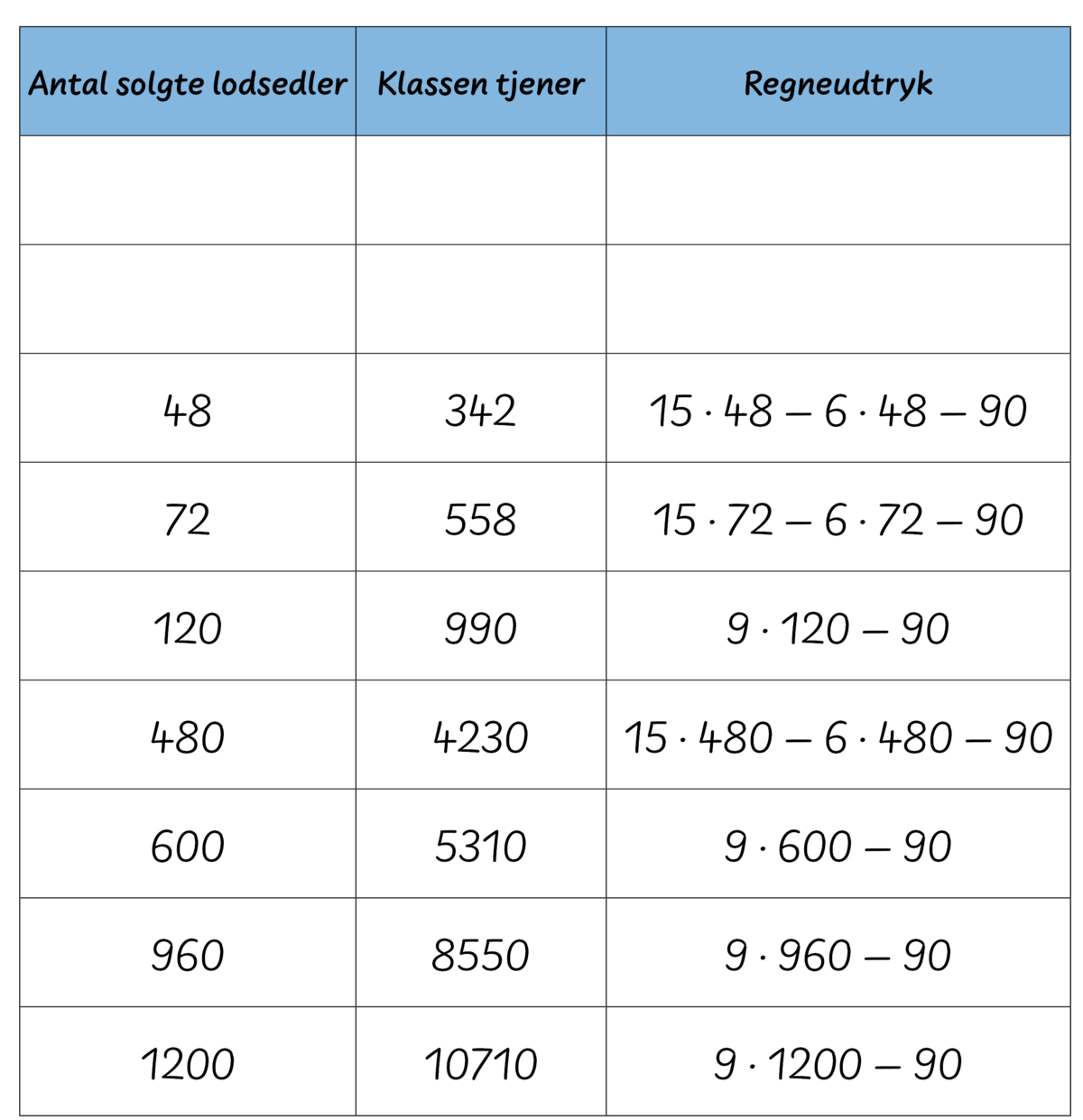
I fællesskab udfylder de tabellen i Figur 10. Med udgangspunkt i tabellen kan læreren rejse forskellige problemstillinger. Læreren kan fx spørge: ”Kan I risikere at få underskud på salget?” og ”Hvor mange lodsedler skal I sælge for at få overskud?” for at udfylde huller for de små antal i tabellen. Elevsvar i stil med ”Hvis vi ingen sedler sælger, så tjener vi ikke noget, men har brugt $90$ på fx bus” og ”Hvis vi sælger $10$ sedler, så tjener vi $0$. Så vi skal sælge mere end $10$ sedler for at få overskud” er værd at fremhæve. Læreren kan bede eleverne om at begrunde disse svar med regneudtryk. Læreren kan også fremskynde pointen, at $0$ er den mindste værdi for antal solgte sedler, men at der i princippet ikke er en øvre grænse for, hvor mange sedler klassen kan sælge. Læreren kan også vælge at sætte fokus på de to forskellige regneudtryk i tabellen og fx bede klassen forklare, hvorfor $15\cdot 480 - 6\cdot 480 - 90$ og $9\cdot 480 - 90$ giver samme resultat. Det er en oplagt anledning til at forklare den distributive lov. Det kan gøres ud fra omskrivningen $15\cdot 480 - 6\cdot 480 - 90 = (15 - 6)\cdot 480 - 90 = 9\cdot 480 - 90$. Klassen kan eventuelt omskrive alle regneudtrykkene i Figur 10 til formen $9\cdot 480 - 90$.
I tabellen i Figur 10 er regneudtrykkene skrevet som $9$ gange antal solgte sedler og ikke som antal solgte sedler gange $9$. Eleverne kan foreslå den sidste skrivemåde, og læreren kan vælge at bruge denne skrivemåde, da den svarer til at addere $9$ med sig selv for hver solgt lodseddel og dermed formodentlig stemmer bedre overens med den måde, som eleverne tænker om situationen. Senere i fase 2 eller 3 kan læreren tale med klassen om, at det ikke betyder noget for resultatet, hvilken skrivemåde der benyttes, da faktorernes orden er ligegyldig ved multiplikation, og at $9$ gange antal solgte sedler er den gængse måde at skrive det på.
Brug og sammenligning af repræsentationer
Læreren kan udfordre klassen ved at spørge: ”Hvor mange lodsedler skal I som klasse sælge for at tjene $2250$ kr.? Det er det beløb, vi mangler for at kunne finansiere jeres lejrtur. I skal begrunde jeres svar med en tabel, en graf og med regneudtryk”. Blandt elevernes svar kan læreren med fordel vælge dem ud til en fælles klassesamtale, som har potentiale til at etablere følgende pointer:
- Jons gruppe har lavet en tabel i et regneark, hvor vi kan se, at det ,klassen tjener, vokser med $9$ kr., når de sælger én seddel mere. Det vokser altså med $9$ kr. fra én række til den næste. Gruppen har lagt $9$ kr. til, indtil de nåede $2250$ kr. Det var, når de havde solgt $260$ sedler. At lave en tabel er en brugbar måde at løse problemet, men det kan være lidt besværligt at gøre. Eller man kan starte med at gætte på antal sedler, og så kan man justere sit gæt op eller ned, hvis man skal finde et bestemt beløb, som klassen kan tjene.
- Emmas gruppe har også lavet en tabel, men i stedet for at fortsætte med at lægge $9$ kr. til hver række i tabellen, så har de tegnet en ret linje igennem tabellens første fem punkter. Dernæst har de forlænget denne linje, indtil de når $2250$ kr. på $y$-aksen, og så har de aflæst på $x$-aksen, hvor mange lodsedler de skal sælge. Egentlig er det mere korrekt kun at tegne punkter på en ret linje og ikke selv linjen. Det er det, fordi vi jo ikke kan sælge en ½ seddel eller en ¼ seddel. Vi kan kun sælge et helt antal sedler.
- Sofus’ gruppe har brugt regneudtrykket $9$ gange antal sedler minus $90$. De har stillet det op som en ligning $9\cdot l - 90$, hvor de har skrevet $l$ for antal solgte sedler. Så har de sat denne ligning lig med $2250$ og løst den. Så man kan altså også bruge regneudtrykkene til at se et mønster og så bruge dette mønster – som er en ligning – til at finde antal sedler.
Senere, fx når klassen arbejder med salg af lodsedler for sportsklubben eller i deres andet gennemløb af fase 1, kan læreren bede eleverne om at sammenligne de tre repræsentationer: graf, tabel og regneudtryk. Her er der flere pointer, læreren kan styre efter, fx:
- Når vi ikke sælger nogen lodsedler, svarer det til det sted, hvor grafen skærer y-aksen. I regneudtrykket svarer det til, at vi ikke har en indtjening, men har en udgift på $90$ – vi trækker altså $90$ fra – og i tabellen svarer det til den første række.
- Når vi ikke tjener noget, så svarer det til det sted, hvor grafen skærer $x$-aksen. I regneudtrykket svarer det til, at resultatet er $0$, og i tabellen at ’Det klassen tjener’ er $0$.
- Kolonner i tabellen svarer til grafens akser. Antal solgte sedler svarer til $x$-aksen, og det, klassen tjener, svarer til $y$-aksen.
- Både i tabellen og på grafen kan vi se, at det, klassen tjener, vokser med $9$ kr., når de sælger en seddel mere. Det kalder vi for grafens hældning. I regneudtrykkene kan vi se det, klassen tjener per seddel, som det tal, vi hver gang ganger med, altså $9$.
- Tabellen kan give et godt overblik. Man kan starte med $0$ sedler og dernæst $1,2,3, …$ Det kan give en god fornemmelse af problemet. Eller man kan starte med at gætte på antal sedler, og så kan man justere sit gæt op eller ned, hvis man skal finde et bestemt beløb, som klassen kan tjene.
- Grafen giver et godt overblik, og det er hurtigt at finde det, vi kan tjene ved at sælge et bestemt antal sedler, og omvendt er det også hurtigt at finde, hvor mange sedler vi skal sælge for at tjene noget bestemt.
- Når vi bruger regneudtryk, kan vi hurtigt finde, hvad vi tjener ved at sælge et bestemt antal sedler. Det bliver også præcist. Grafen kan nogle gange være sværere at aflæse. Vi kan også finde, hvor mange sedler som vi skal sælge for at tjene noget bestemt, ved at opstille en ligning ud fra regneudtrykkene og løse den.
I fase 1 skal funktionssituationen give klassen mulighed for at skabe tæt sammenhæng mellem de fire repræsentationer: sproglige beskrivelser, tabeller, regneudtryk og grafer. I Lodsedler giver det fx mening, at $x$ er $0$ både i forhold til funktionssituationen, i tabeller, i beregninger og grafisk som skæring med y-aksen. Dermed støttes eleverne i at bruge de forskellige repræsentationer og at oversætte fleksibelt mellem dem. I de andre gennemløb af fase 1 tilstræbes at lave tilsvarende tætte og meningsfulde koblinger mellem de fire repræsentationer gennem valg af funktionssituation.
Fase 2
I fase 2 bruger klassen deres regneudtryk fra fase 1 til at beskrive den lineære sammenhæng med en forskrift på formen $l(x) = ax + b$, hvor $a$ og $b$ er specifikke tal. Det skal de gøre ved at genkende et mønster i regneudtrykkene. De første gange, klassen gennemløber fase 2, er der brug for forklaringer og støtte fra læreren. Læreren kan med fordel introducere notationen $l(x)$, så eleverne kan skelne mellem de forskellige funktioner, de arbejder med. Det er vigtigt, at læreren støtter eleverne i at koble forskrift til tabel og graf.
I eksemplet vises, hvordan læreren kan støtte eleverne i at beskrive sammenhængen med en forskrift og i at skabe mening med den algebraiske notation.
Fase 2
At oversætte sproglige beskrivelser, tabeller, regneudtryk og grafiske repræsentationer af lineære sammenhænge til forskrifter.
Udvikling af forskrift
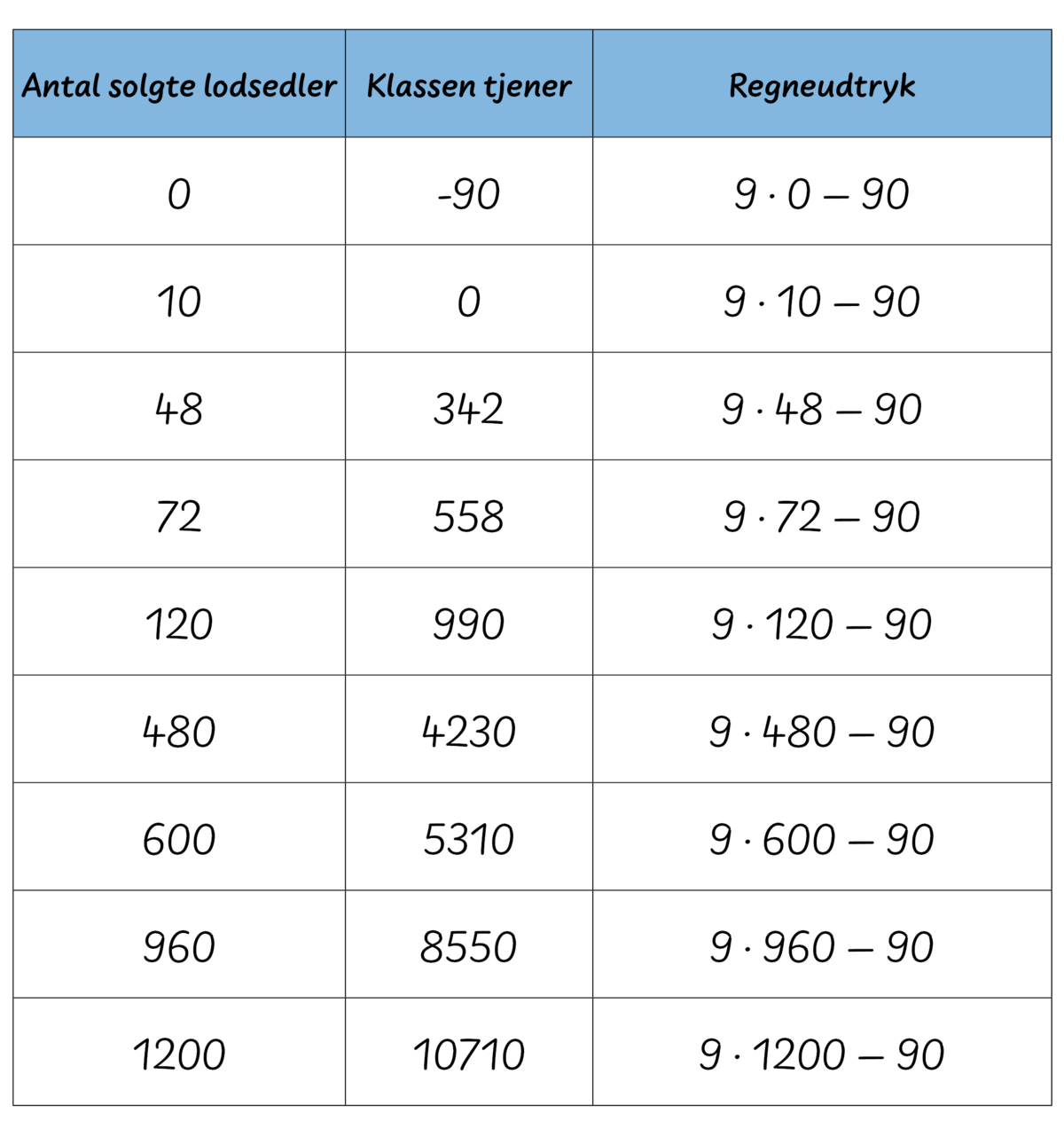
Læreren kan tage udgangspunkt i elevernes regneudtryk i Figur 10. Klassen kan starte med at omskrive regneudtrykkene til kort form som i Figur 11, hvis de ikke allerede har gjort det. Læreren kan tale med klassen om, hvilket mønster de kan få øje på i regneudtrykkene, og hvordan dette mønster vil fortsætte. Elevsvar som at ”man ganger altid med $9$” eller ”man trækker altid $90$ fra” er vigtige at fremhæve. Dernæst kan læreren introducere forskriften ved at sige:
Man kan skrive det sådan: $l(x) = 9\cdot x - 90$. Det her udtryk kalder man en forskrift for funktionen. Den kan man bruge til at beregne, hvor meget vi kan tjene, når vi sælger lodsedler for en velgørenhedsorganisation.
Læreren kan drøfte med klassen, hvad $x$ og $l(x)$ står for, hvad $9$ og $90$ står for, og hvad $l(0), l(10), l(48)$ osv. betyder. De kan også drøfte, hvordan forskriften ville se ud, hvis engangsudgifterne var $75$ kr. eller $150$ kr., eller hvis de kunne tjene $25$ kr. eller $3$ kr. per seddel. I samtalen kan læreren knytte de nye symboler $x$ og $l(x)$ til den tabel, klassen har lavet, og skrive $x$ i kolonnen for antal solgte lodsedler, $l(x)$ i kolonnen for det klassen tjener og forskriften i kolonnen med regneudtryk. I samtalen kan følgende pointer være centrale at få frem:
- Grunden til at man skriver $l(x)$ og ikke $l$ er, at denne funktion afhænger af $x$. Prøv at se i tabellen. Hvis $x$ fx er $120$ – det vil sige at I sælger $120$ lodsedler – så kan $l(x)$ kun være $990$ kr. Vi kan altså ikke tjene mere eller mindre end $990$ kr., hvis vi sælger $120$ sedler. Så hvor meget vi tjener, det afhænger af, hvor meget vi sælger. Så man siger, at $l(x)$ afhænger af $x$. Derfor kaldes $l(x)$ også for den afhængige variabel, mens $x$ kaldes for den uafhængige variabel.
- Nu har vi kaldt funktionen for $l(x)$, fordi det handlede om salg af lodsedler. Men jeg kunne også have valgt at kalde den et andet bogstav eller et navn, fx $lodsedler(x)$. Her i starten må I gerne bruge sådanne navne, hvis I synes det er nemmere at forstå.
Eleverne støttes i at forstå og udvikle algebraisk notation, hvis de selv kan vælge navne eller bogstaver. Når de er blevet fortrolige med notationen, så kan de gængse bogstaver for funktioner og variable introduceres såsom $f(x), g(x), h(x), n$ og $x$. Ofte bruges $n$ som symbol for en uafhængig variabel, der er et naturligt tal, og ellers bruges $x$. Hvis eleverne ikke selv begynder at bruge symboler, må de opfordres til det, og ofte må læreren introducere dem.
Klassen kan arbejde på samme måde med at bestemme forskriften for sammenhængen mellem lodsedler og klassens indtjening, når de sælger lodsedler for sportsklubben. Det er vigtigt, at eleverne finder et andet navn for denne forskrift end $l(x)$, fx $h(x)$, for at kunne skelne mellem de to funktioner. Behovet for at kunne skelne mellem disse to er den primære grund til, at notationen introduceres i fase 2. Det er vigtigt, at eleverne forstår, at antal solgte lodsedler stadig er $x$ – det ændrer ikke navn.
I fasen kan klassen også koble forskrifterne til de andre repræsentationer fra fase 1; tabel og graf. Dette vil styrke elevernes forståelse af forskriften og sammenhængene mellem repræsentationerne. Læreren kan fx spørge klassen til betydningen af tallene $9$ og $-90$ i forskriften: Hvor kan I se $-90$ på grafen? Og $9$? Hvor finder I de to tal i tabellen? Og i jeres beregninger? Hvordan hænger disse tal sammen med antal solgte lodsedler og det, klassen tjener?
Efter hver gennemløb af de første to faser skal eleverne producere en plakat, hvor de beskriver og forklarer deres oversættelser af den funktionssituation, de har arbejdet med, til tabel, regneudtryk, graf og forskrift. Disse plakater danner udgangspunkt for klassens arbejde i fase 4.
Fase 3
I fase 3 sammenligner klassen de lineære sammenhænge, som de har arbejdet med i fase 1 og 2, ved at bruge repræsentationerne fra disse faser: tabeller, grafer, forskrifter og ligninger. Fokus er på at sammenligne ved at løse ligninger grafisk og algebraisk, og eleverne kan danne mening hermed, hvis de arbejder med funktionssituationer, som de kender og tidligere har arbejdet med grafisk.
Eksemplet viser, hvordan en klasse kan sammenligne, om det bedst kan betale sig for dem at sælge lodsedler for velgørenhedsorganisationen eller for sportsklubben.
Fase 3
At sammenligne lineære sammenhænge ved hjælp af tabeller, grafer, forskrifter og ligninger.
Sammenligning af lineære sammenhænge
Klassen skal finde ud af, om de kan tjene flest penge ved at sælge lodsedler for en velgørenhedsorganisation eller for sportsklubben. I lærerens iscenesættelse bliver det klart, at det er smart først at finde ud af, hvor mange sedler klassen skal sælge for at tjene det samme. Eleverne opfordres til at bruge tabeller, grafer, forskrifter og ligninger.
-
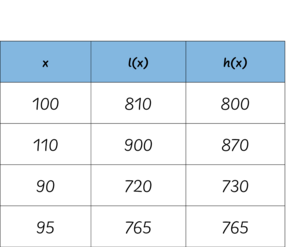
Nogle elever bruger tabellerne til at gætte sig frem til en løsning. De gætter først på, at klassen skal sælge $100$ sedler, og beregner, hvor meget klassen kan tjene for hvert af de to tilbud (se Figur 12). De kan se, at de er tæt på, og justerer deres gæt – først skyder de lidt over, dernæst lidt under, og til sidst rammer de det rigtige antal lodsedler, $95$.
-
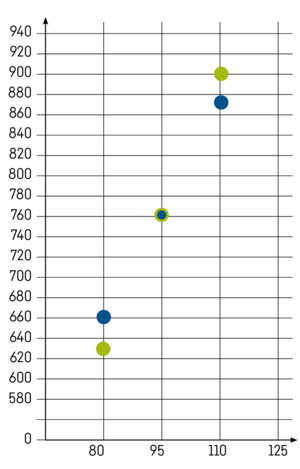
Andre elever bruger også tabeller, men til at tegne punktgraferne for de to lineære sammenhænge. De ser, at hvis klassen sælger $95$ sedler, så tjener de $765$ kr. hos velgørenhedsorganisationen og sportsklubben, men at det ved større salg bedst kan betale sig at sælge for velgørenhedsorganisationen. Deres grafiske løsning svarer til at finde skæringspunkter mellem de to grafer (se Figur 13).
Hvis eleverne ikke foreslår løsning med brug af ligninger, kan læreren introducere den ud fra den grafiske løsning, fx i stil med:
I dette punkt sælger I $95$ lodsedler, og I tjener det samme, uanset om I sælger for velgørenhedsorganisationen eller sportsklubben [peger på skæringspunktet for de to grafer]. I kan finde punktet ved at aflæse dets koordinater, som Ahmed og hans gruppe har gjort, og i GeoGebra kan I aflæse det præcist. Men I kan også bruge de to forskrifter, som vi har fundet. I dette punkt tjener jeres klasse jo lige meget – det vil sige, at værdien af $l(x)$ og $h(x)$ er den samme i dette punkt. Vi kan derfor prøve, om vi kan finde en x-værdi, som gør, at lighedstegnet gælder. Vi ved, at $l(x)$ er $9 \cdot x - 90$, og $h(x)$ er $7 \cdot x + 100$, så den ligning, vi skal løse, er $9 \cdot x - 90 = 7 \cdot x + 100$. Ligner det noget, I tidligere har set? Ja, det ligner de ligninger, som vi arbejdede med sidste år. Hvis vi løser denne ligning – altså finder $x$ – så har vi fundet det antal lodsedler, som klassen skal sælge for at tjene lige meget. Giver det mening? Prøv at løse den.
Det er vigtigt, at læreren således fokuserer på at støtte eleverne i at skabe sammenhæng mellem den grafiske repræsentation og det algebraiske udtryk (ligningen). Eleverne kan bedst skabe disse sammenhænge i situationer, hvor løsningen af ligningen ikke tager alt deres opmærksomhed. I en klassesamtale om elevernes forslag til, hvad der bedst kan betale sig for klassen, er det vigtigt, at pointer i stil med disse bliver tydelige:
-
Den grafiske løsning giver et godt overblik af sammenhængen mellem de to tilbud. Når jeres klasse sælger mange lodsedler, så kan vi godt forsvare at tegne en ret linje mellem punkterne, fordi de ligger så tæt. Vi skal selvfølgelig bare vide, at man jo ikke kan sælge ½ seddel, så det er ikke en ret linje, hvis vi zoomer ind.
-
Det er nødvendigt at lave en tabel for at konstruere en graf. Hvis man ikke har et godt gæt – som fx Emmas gruppe – så kan det være tidskrævende at bruge tabellen til at finde løsningen.
-
Hvis I har de to forskrifter, kan I finde løsningen ved at sætte dem lig med hinanden og finde en x-værdi, som gør, at lighedstegnet gælder. I behøver ikke tegne graferne først.
I resten af fase 3 kan klassen arbejde videre med andre spørgsmål knyttet til at sammenligne de to måder at tjene penge på ved salg af lodsedler. Det kan fx være spørgsmål som:
-
Hvor mange lodsedler skal klassen sælge for velgørenhedsorganisationen og sportsklubben, hvis de vil tjene $3000$ kr.? Det er vigtigt, at klassen løser flere af sådanne problemer både grafisk ved aflæsning (eller ved brug af et Dynamisk Geometri System) og algebraisk ved at løse ligninger såsom $3000 = 9 \cdot x - 90$ og $3000 = 7 \cdot x + 100$.
-
Hvad er det mindste klassen kan tjene for velgørenhedsorganisationen og sportsklubben? Hvordan kan man se det på grafen og i forskrifterne? Hvilken sammenhæng er der mellem graferne og forskrifterne? Hvordan kan man på grafen se, at en lodseddel kan sælges for $9$ kr. eller $7$ kr.? I forskrifterne? Spørgsmål af denne typer skal støtte eleverne i at forstå de to typer af repræsentationer og deres sammenhæng og i at kunne skifte fleksibelt fra den ene repræsentation til den anden.
-
Hvorfor er grafen for velgørenhedsorganisationen mere stejl end den anden graf? Hvordan kan en anden graf, der er mere stejl, mindre stejl eller ikke stejl (vandret linje) se ud? Spørgsmål af denne typer skal støtte eleverne i at udvikle forståelse for hældningen af en graf, og hvordan størrelsen af den har betydning for grafens udseende. Tilsvarende spørgsmål kan stilles til grafens skæring med $y$-aksen.
Læreren kan overveje, om nogle eller alle eleverne skal udvide deres plakater med noget af det, som de har arbejdet med i fase 3, fx hvordan man kan bestemme skæringspunktet mellem to rette linjer, og/eller hvad sammenhængen er mellem forskriften for en funktion og dens graf. I de efterfølgende gennemløb af fase 3 kan klassen løse ligninger med rationale tal og reelle variable.
Fase 4
Fase 4 tager udgangspunkt i de plakater, som klassen har produceret i hvert af deres gennemløb af faserne 1-3. Plakaterne beskriver forskrifter for konkrete lineære funktioner, hvor parametrene $a$ og $b$ varierer – fra positive heltal over negative tal til rationale tal. Ved at se på mønstre i disse forskrifter kan klassen med lærerens støtte generalisere dem til forskriften for en lineær funktion, $f(x) = a \cdot x + b$. Fasen lægger også op til, at klassen undersøger egenskaber ved lineære funktioner, bl.a. betydningen af $a$ og $b$ for grafens udseende.
Eksemplet viser, hvordan læreren kan støtte eleverne til at opdage mønstre i de funktionsforskrifter, som de tidligere har udviklet, og at generalisere dem til standardformen for en lineær funktion.
Fase 4
At generalisere konkrete forskrifter til standardformen for en lineær funktion, $f(x)=a \cdot x + b$, og undersøge betydningen af parametrene $a$ og $b$.
Udvikling af den generelle forskrift
I det gennemgående eksempel om Lodsedler kan læreren bede eleverne om at hænge deres plakater op, så alle de funktioner, som klassen har arbejdet med, er synlige. Samtidig skriver læreren forskrifterne for funktionerne op på tavlen (se Figur 14). Klassen kan have brug for at tale om de enkelte forskrifter for lige at genkalde sig det, de tidligere har arbejdet med. Læreren beder dernæst eleverne om at se efter mønstre i forskrifterne. En dialog i stil med den følgende kan dernæst udspille sig:
Lærer: Hvad lægger I mærke til? Er der noget, som går igen i alle forskrifterne? Hvad er ens, og hvad er forskelligt ved forskrifterne?
Sofia: De har alle sammen et bogstav og så $x$ i parentes til at starte med og et $x$ på den anden side.
Lærer: Ja, navnet på funktionerne, som vi kaldte et bogstav, og så $x$ i parentes [peger på navnene] står på venstre side af lighedstegnet, mens $x$ – det som funktionerne afhænger af – står på højre side. Ja, Otto?
Otto: Der er også altid to tal på højresiden – et tal, som ganges med $x$, og et tal, som står alene.
Lærer: Ok, så Otto kan se et mønstre i tallene også. Der er altid et tal, der skal ganges med $x$, og et tal, der står alene.
Ahmed: Det passer ikke. I $j(x)$ er der ikke et tal foran $x$.
Lærer: Her står $-x$. Det er jo rigtig; her er ikke et tal foran $x$. Hmm … kan vi omskrive det, så der står et tal foran $x$, som $x$ skal ganges med? [ingen elever markerer]. Hvad hvis jeg skriver $-1 \cdot x$ i stedet for? Er det det samme? [skriver det på tavlen].
Ahmed: Ja. Cool.
Lærer: De mønstre, I foreslår, er altså, at vi i eksemplerne enten skal gange $x$ med et positivt tal eller med et negativt tal, og så skal vi enten trække et andet tal fra eller lægge det til. I er gode til at finde måder, som de er ens på. De her funktioner beskriver alle én bestemt situation, fx beskriver $l(x)$, hvad en 7. klasse kunne tjene, hvis de solgte $x$ lodsedler for en velgørenhedsorganisation. Kan I huske det? Eksemplerne referer hver især til forskellige situationer, men samtidig har I jo peget på, at de også er ens. Man kan oversætte eller generalisere disse udtryk til en forskrift, der gælder for alle sådanne funktioner, uanset om det handler om at tjene penge ved at sælge lodsedler eller om at bestemme afstanden mellem havet og et fyrtårn. Kan I hjælpe mig med at finde den forskrift ud fra det, I har sagt?
Ahmed: Jeg forstår overhovedet ikke, hvad du mener.
Lærer: Ok, hvis jeg nu kalder det tal, som man skal gange med $x$ for $a$, så skriver jeg $a$ her [skriver forskriften langsomt op nedenunder]. Og hvis jeg så kalder det andet tal for $b$, hvad skal jeg så skrive?
Ahmed: Åh … $+b$.
Lærer: Ja [skriver på tavlen (se Figur 15)]. Så bliver det $f(x)=a \cdot x+b$. Så alle de her tal, jeg ganger med $x$ [sætter ring om nogle af dem og en pil ned til $a$], de er alle en af de værdier, som $a$ kan have, mens det jeg lægger til [sætter ring om nogle af dem og en pil ned til $b$], de er alle en af de værdier, som $b$ kan have. Det er ikke helt let at forstå denne forskrift. Prøv at tale med jeres sidemakker om den, og skriv det, I ikke forstår eller er usikre på, ned som spørgsmål. Så taler vi om det bagefter.
Pointen med dialogen er at vise, hvordan læreren kan styre den fælles klassesamtale hen mod det, der er ens for alle de lineære sammenhænge, som klassen har arbejdet med, og hvordan læreren med udgangspunkt i det, eleverne byder ind med, kan introducere det generelle udtryk for en lineær funktion. I dialogen foreslår læreren at bruge $a$ til at beskrive det tal, som $x$ skal multipliceres med. I andre klasser kan det være, at elever selv foreslår $a$ eller et andet bogstav.
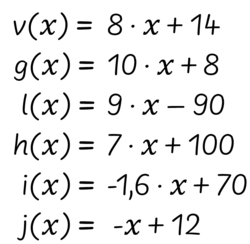
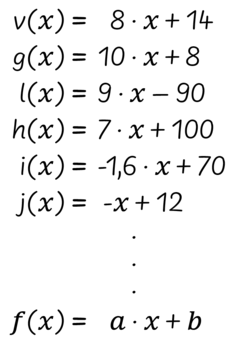
I resten af fase 4 er det en god idé at give klassen mulighed for (støttet af læreren) at skabe mening med $a$ og $b$ og strukturen i den generelle forskrift ud fra deres erfaringer fra de tidligere faser og gennem ræsonnementer. Det kan eleverne gøre, når de arbejder med problemstillinger såsom:
-
At udforske sammenhængene mellem $a$ og $b$ i den generelle forskrift og den rette linje for funktionen. Hvor på grafen kan I finde $b$? Og $a$? Hvad sker der med grafen, hvis $b$ vokser eller bliver mindre eller er $0$? Hvad sker der med grafen, hvis $a$ vokser eller bliver mindre? Klassen kan eventuelt udforske disse sammenhænge i et Dynamisk Geometri System og bruge en skyder for $b$ og for $a$. Det centrale her er, at eleverne kan skabe sammenhæng og mening mellem den generelle forskrift og dens graf, så de kan skifte fleksibelt mellem de to repræsentationer. Eleverne kan fx opdage, at $f(0) = b$ svarer til linjens skæring med y-aksen, at $f(x) = 0$ svarer til linjens skæring med $x$-aksen, og at fortegnet på $a$ bestemmer om graften er positiv eller negativ, når $x$ er stor.
-
At oversætte forskrifter til grafer og omvendt – uden at lave tabeller. Denne problemstilling ligger i forlængelse af den første problemstilling og sætter fokus på sammenhængen mellem en funktions forskrift og graf. Elever kan styrke deres forståelse af grafens hældning $a$ og skæring med y-aksen $b$ gennem øvelsen.
-
At udforske egenskaber ved parallelle lineære funktioner, dvs. funktioner med en bestemt $a$-værdi, men hvor $b$-værdierne er forskellige, fx $f(x) =\frac{2}{3} \cdot x + b$, ved at tegne dem for udvalgte $b$-værdier. Eleverne kan fx opdage, at graferne er rette linjer med samme hældning, men at deres skæring med y-aksen afhænger af $b$-værdien, og at man kan komme fra én funktion til en anden ved at lægge forskellen i $b$-værdierne til eller trække den fra.
-
At udforske egenskaber ved konstante lineære funktioner, fx $f(x) = b$, hvor $a$ er $0$. Klassen kan tegne graferne for konstante funktioner, fx $f(x) = 3$ og $g(x) = -\frac{4}{5}$, og undersøge sammenhængen mellem forskriften og dens graf. Eleverne kan også oversætte den konstante funktion til en funktionssituation for at styrke deres forståelse af funktionsbegrebet.
-
At ræsonnere om sammenhængen mellem forskrifter og deres grafer. Klassen kan præsenteres for forskellige forskrifter og deres grafer og skal finde ud af, hvilken graf der passer med hvilken forskrift. Samme øvelse kan laves med de andre repræsentationer – sproglige beskrivelser og tabeller – hvor repræsentationerne kan kobles på kryds og tværs. Det styrker elevernes forståelse af repræsentationerne og deres sammenhænge.
-
At oversætte sproglige beskrivelser i form af funktionssituationer til forskrifter og omvendt. Læreren kan præsentere klassen for nye funktionssituationer og drøfte med eleverne, hvad der varierer i situationerne, og om noget af det, der varierer, afhænger af noget andet, der varierer. På den måde kan den uafhængige variabel $x$ og funktionen, der afhænger af $x$, findes. Eleverne skal også finde værdierne for $a$ og $b$ – her er vigtigt at tale med klassen om, hvad $a$ og $b$ beskriver – og skrive forskriften op. Eleverne kan også styrke deres forståelse af algebraisk notation ved at oversætte en forskrift til en sproglig beskrivelse.
-
Et mere udfordrende problem er at give (nogle) elever to punkter i et koordinatsystem og bede dem om at finde forskriften for den rette linje, der går igennem punkterne.
I denne sidste fase er det vigtigt, at det står klart for eleverne, hvad der kendetegner en lineær funktion. Læreren kan understrege disse kendetegn undervejs i fasen, hvor det giver mening, og/eller afslutte fasen med at samle op på det, fx ved at sige noget i stil med:
Vi har i de sidste uger arbejdet med en særlig type af funktioner. Det er funktioner, der vokser med et bestemt tal, som vi har kaldt $a$, hver gang $x$ vokser med $1$. I eksemplet med Lodsedler kunne I fx tjene $9$ kr., hver gang I solgte en lodseddel mere – I kunne altså lægge $9$ kr. til jeres fortjeneste for hver seddel, I solgte. Man siger derfor, at funktionen vokser med $9$ kr. per seddel. Disse funktioner kalder man for lineære funktioner. Man kalder dem lineære funktioner, fordi deres graf er en ret linje. Der findes andre funktioner, som ikke vokser på denne måde, og som derfor ikke er lineære, fx når I skal finde det beløb, der står på jeres opsparingskonto, efter at I har fået renter. Her lægger man ikke det samme tal til hver gang, man får renter, men en procentdel af beløbet. Det skal vi snakke mere om senere.