Tilgang – At finde sammenhænge mellem tal
I dette læringsspor arbejder en klasse i gentagne gennemløb med faserne. I første gennemløb kommer formentlig kun fase 1 og 2 i spil. I de næste gennemløb kan det tænkes, at fase 1, 2 og 3 kommer i spil. Efter flere gentagelser – fordelt over flere skoleår – kommer både fase 1, 2, 3 og 4 i spil. En klasse begynder altså gentagne gange forfra i faserne. For hvert gennemløb øges både antallet af faser og de faglige udfordringer. Figur 3 illustrerer, hvordan det antal faser, der indgår i hvert gennemløb, kan være forskellig på forskellige klassetrin.

Fase 1
Hvert gennemløb i læringssporet tager udgangspunkt i såkaldte funktionssituationer. En funktionssituation er en situation, hvor (mindst) én uafhængig og én afhængig variabel varierer sammen (Smith, 2008). Sådanne situationer kan både vedrøre en ren matematisk kontekst og en omverdenkontekst. Det afgørende er, at eleverne får gode muligheder for at forestille sig situationen, undersøge den og for at opdage og beskrive sammenhænge mellem tal, der varierer sammen.
Nedenfor gives to eksempler på funktionssituationer:
Eksempel på funktionssituation i en ren matematisk kontekst
Rektangler med fast sidelængde
Tegn mindst 5 forskellige rektangler på ternet papir. Den ene sidelængde skal være 4. Den anden sidelængde bestemmer du selv.

Hvad er sammenhængen mellem den frie sidelængde og antallet af tern i sådan et rektangel?
Eksempel på funktionssituation i en omverdenkontekst
Borde og stole
Se på tegningerne. Hvor mange stole passer til 1 bord? 2 borde?

Hvordan fortsætter det, hvis man stiller flere borde på række?
Hvor mange stole skal man bruge til 10 borde?
Til et eller andet antal borde?
I fase 1 af læringssporet afprøver eleverne den ukendte funktionssammenhæng med forskellige tal.
I problemstillingen fra eksempel 1 kan man fx forestille sig, at en elevgruppe tegner et rektangel, der har sidelængderne 4 og 10. De tæller sig frem til, at sidelængden på 10 medfører, at der er 40 tern i rektanglet. 10 og 40 er altså to tal, der hænger sammen og udgør et talpar i denne situation. På tilsvarende vis kan man forestille sig, at eleverne finder andre talpar, fx 5 og 20, 8 og 32 osv. Måske finder de med lærerens støtte ud af, af de ikke behøver at tælle sig frem til antallet af tern. De kan skyde genveje ved at lægge tal sammen.
I problemstillingen fra eksempel 2 kan man fx forestille sig, at en elevgruppe finder ud af, at de skal bruge 6 stole til 1 bord, 10 stole til 2 borde, 14 stole til 3 borde osv. De bruger optællinger og beregninger til at finde nogle talpar i situationen. På den måde får de nogle erfaringer, som de kan trække på, når de senere skal beskrive den generelle sammenhæng mellem antal borde og stole.
Fase 1
At finde talpar i funktionssituationer med lineære sammenhænge.
En funktionssituation er en situation, hvor (mindst) én uafhængig og én afhængig variabel varierer sammen (Smith, 2008).
Fase 2
I fase 2 er der fokus på, at eleverne opstiller de talpar, de har fundet, i en funktionstabel, og at de bruger regneudtryk til at vise, hvordan de har fundet frem til de tal, der hører sammen. I begyndelsen af læringssporet har eleverne derfor behov for, at læreren introducerer disse måder at beskrive sammenhænge på.
En funktionstabel kan enten være uordnet eller ordnet. I forbindelse med problemstillingen fra eksempel 1 kan begyndelsen på en fælles tabel i en 2. klasse fx komme til at se ud på disse måder:

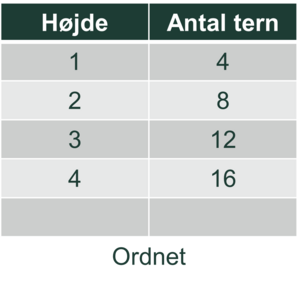
Fase 2
At beskrive lineære sammenhænge med funktionstabeller og regneudtryk.
Ved at kigge lodret i den ordnede tabel kan eleverne fx få øje på, at tallene i venstre kolonne bliver 1 større i hver række, og at tallene i højre side bliver 4 større. Elevernes erfaringer fra fase 1 giver dem mulighed for at forstå, hvad disse mønstre fortæller om rektanglerne. De kan fx sige: ’Antallet af tern bliver hele tiden 4 større’. Den ordnede tabel kan med andre ord give eleverne mulighed for at opdage en rekursiv sammenhæng, der gælder generelt.
Den ordnede tabel giver også eleverne mulighed for at fokusere på, hvordan tallene i venstre og højre kolonne varierer sammen, dvs. hvordan højden af et rektangel og antallet af tern varierer sammen. Når højden bliver 1 større, bliver antal tern 4 større. Den ordnede tabel giver med andre ord eleverne mulighed for at opdage en samvariation, der gælder generelt.
Den uordnede tabel giver ikke så gode muligheder for at se mønstre, men den kan give anledning til at fokusere på korrespondancesammenhængen (den vandrette sammenhæng): ’Hvordan kan man finde antallet af tern, når man kender højden?’. Læreren kan guide eleverne i den retning ved at spørge, hvordan de fandt antallet af tern i rektanglerne. Det er sandsynligt, at nogle elever vil svare fx: ’Jeg tegnede en med højden 10. Så sagde jeg $10+10+10+10$, for der var fire rækker med 10. Det blev 40’. Eleven formulerer på den måde et regneudtryk, som læreren kan skrive ($10+10+10+10$). Med lærerens støtte får eleverne mulighed for at se, at denne fremgangsmåde kan bruges generelt: ’Hvordan kan I bruge samme idé, hvis højden er 2?’. Svaret på dette spørgsmål kan også give anledning til at skrive et regneudtryk ($2+2+2+2$). Efterhånden kan der opstå en hel samling af regneudtryk, der har en bestemt struktur, som eleverne kan opdage ($1+1+1+1$, $2+2+2+2$, $3+3+3+3$ osv.). Regneudtrykkene kan med andre ord give eleverne mulighed for at opdage en korrespondancesammenhæng, der gælder generelt.
En rekursiv sammenhæng kan opfattes som den lodrette sammenhæng i en ordnet funktionstabels kolonne, fx ’Den vokser hele tiden med 4’ (Smith, 2008).
Samvariation kan opfattes som en kombination af den lodrette og den vandrette sammenhæng i en ordnet funktionstabel, fx ’Når den ene vokser med 1, vokser den anden med 4’ (Smith, 2008).
En korrespondancesammenhæng kan opfattes som den vandrette sammenhæng i en funktionstabel, fx ’Man skal lægge det ene tal sammen 4 gange, så får man det andet tal’ (Smith, 2008).
Fase 3 og 4
I fase 3 og 4 er der fokus på, at eleverne opdager, beskriver og begrunder sådanne generelle sammenhænge. Som det fremgår af det forrige, kan ordnede tabeller og regneudtryk støtte eleverne til opdagelserne.
I de første gennemløb af læringssporet, dvs. i 2.-3. klasse, er forventningen, at eleverne beskriver deres opdagelser af generelle sammenhænge gennem taleksempler og med deres hverdagssprog, dvs. som faktuelle og kontekstuelle generaliseringer. I de sidste gennemløb af læringssporet, dvs. i 5.-6. klasse, er det forventningen, at eleverne beskriver generelle korrespondancesammenhænge med algebraisk notation.
Eksempel (faktuel generalisering, fase 3):
Fase 3
At opdage, begrunde og beskrive generelle lineære sammenhænge faktuelt og kontekstuelt.
Fase 4
At opdage, begrunde og beskrive generelle lineære sammenhænge på alsidige måder, bl.a. med bogstavudtryk.
Elev: ’Hvis højden er $10$, kan man finde antal tern ved at regne $10+10+10+10$. Hvis højden er $100$, er det $100 + 100 + 100 + 100$. Hvis den er $1000$, er det…’
Eksempel (kontekstuel generalisering, fase 3):
Faktuelle generaliseringer er mundtlige eller skriftlige beskrivelser af generelle sammenhænge gennem specifikke eksempler (Radford, 2018).
Elev: ’Hvis du vil finde ud af, hvor mange tern der er, kan du tage længden af den der side (peger), og så kan du plusse tallet fire gange’
Kontekstuelle generaliseringer er mundtlige eller skriftlige beskrivelser af generelle sammenhænge med tæt reference til de rumlige eller kontekstuelle elementer, som generaliseringen handler om (Radford, 2018).
Eksempel (generalisering med bogstavudtryk, fase 4):
Elev: ’Hvis $h$ er højden, og $t$ er antal tern, så er $4 \cdot h = t$’
Det er en vigtig pointe, at de forskellige måder at beskrive på kan eksistere side om side i klassen, sådan at forskellige elever kan beskrive deres generaliseringer på forskellige måder. Det er målet, at alle elever bliver fortrolige med at bruge og tænke i algebraisk notation, men det sker næppe på samme tid. Desuden giver de faktuelle og kontekstuelle beskrivelser eleverne øgede muligheder for at skabe mening i algebraisk notation.
Eleverne får også muligheder for at skabe mening i algebraisk notation, når de begrunder de generelle sammenhænge, de har opdaget. Begrundelserne skal kæde (generelle) beskrivelser og den tilhørende funktionssituation sammen. De skal give svar på, hvorfor en given beskrivelse gælder for alle eksempler, der kan udspringe af funktionssituationen. Begrundelserne skal derfor bygge på situationen.
Elever kan typisk give begrundelser for en sammenhæng ved at referere til den funktionssituation, der var udgangspunkt for arbejdet. I rektangler med en fast sidelængde kan en elev fx begrunde den generelle sammenhæng sådan: ’Man skal plusse højden med sig selv fire gange, for i hvert rektangel kommer der jo 4 søjler, der er så store. Det bliver 4 søjler, fordi en af siderne skal være 4 lang’. Begrundelsen kan bakkes op af andre udsagn, fx: ’Man kan prøve efter og se, at det passer hver gang’.
Progressionen fra 2.- 6. klasse
Som beskrevet indledningsvist gennemfører eleverne i dette læringsspor flere gennemløb. Hvert nyt gennemløb tager udgangspunkt i en ny funktionssituation, og i hvert gennemløb øges både antallet af faser og de faglige udfordringer.
Som beskrevet i det forrige består en del af den faglige progression i bevægelsen fra faktuelle og kontekstuelle beskrivelser af generelle sammenhænge (fase 3) til beskrivelser med algebraisk notation (fase 4).
En anden vigtig del af den faglige progression består i en udvikling af de funktionssituationer, som eleverne arbejder med i hvert gennemløb. Denne progression kan beskrives i tre kategorier:
- Funktionssammenhænge af formen $f(n)=n+ \cdots + n$, hvor $n$ er et naturligt tal, eller $f(n)=a \cdot n$, hvor både $a$ og $n$ er naturlige tal.
- Funktionssammenhænge af formen $f(n)=n+b$ eller $f(n)=n-b$, hvor både $n$ og $b$ er naturlige tal.
- Funktionssammenhænge af formen $f(n)=a \cdot n +b$ eller $f(n)=a \cdot n - b$, hvor både $a$, $n$ og $b$ er naturlige tal.
I de første runder (2.-3. klasse) arbejder eleverne med sammenhænge af kategori 1. I senere runder (3.-4. klasse) arbejder eleverne med sammenhænge af kategori 2. I de sidste runder (4.-6. klasse) arbejder eleverne med sammenhæng af kategori 3. Eksempler på opgaver af de forskellige kategorier kan ses nedenfor:
Kategori 1
-
Sammenhængen mellem antal børn og antal øjne/ben/arme/fingre
-
Rektangler med en fast sidelængde (som beskrevet i det forrige)
-
Sammenhængen mellem sidelængde og omkreds i et kvadrat
-
Sammenhænge mellem sidelængde og omkreds i andre figurer
Kategori 2
- Sammenhængen mellem to personers aldre
- Sammenhængen mellem højden af et juletræ med og uden en bestemt stjerne i toppen
- Sammenhængen mellem det antal lakridser, et barn får, og det antal lakridser, barnet kan spise, når han/hun skal aflevere 5 til sin lillebror
Kategori 3
- Sammenhængen mellem antal borde og stole i forskellige opstillinger (som beskrevet i det forrige)
- Sammenhængen mellem antallet af centicubes og overfladearealet i ’centicubestænger’ (som beskrevet under mål)
- Sammenhængen mellem antal solgte kopper saftevand og indkomst, når udgifterne er betalt