Praksis – At forstå og anvende lineære funktioner
De tidsmæssige rammer
Sporet dækker emnet i det gymnasiale grundforløb og den videre behandling af lineære funktioner i 1.g samt emnet i 1. hf. Der kan arbejdes med alle fire faser i grundforløbet. Fase 3 og 4 kan der arbejdes uddybende med i den efterfølgende matematikundervisning i 1.g. Læringssporet er designet til at kunne realiseres over 16 sammenhængende undervisningstimer i grundforløbet. Tiden tænkes nogenlunde lige fordelt over faserne. Hertil kommer uddybende arbejde med fase 3 og 4 i efterfølgende matematikundervisning i 1.g svarende til 4-6 undervisningstimer.
Det faglige udgangspunkt
Læringssporet bygger på faglige forudsætninger hos eleverne svarende til sporet om funktioner for 9. klasse og sporet om lineære funktioner til 7.-8. klasse. Her har eleverne arbejdet med at beskrive og forstå konkrete lineære variabelsammenhænge som samvariation og som en korrespondance mellem en uafhængig og en afhængig variabel. Det gælder konkrete sammenhænge, hvor den uafhængige variabel varierer diskret inden for $\mathbb{N}$ eller $\mathbb{Z}$, og sammenhænge, hvor den uafhængige variabel varierer kontinuert inden for $\mathbb{R}$. Eleverne har i disse sammenhænge arbejdet med alle fire repræsentationsformer samt med oversættelse mellem dem. De har opstillet og undersøgt lineære funktioner som modeller for konkrete sammenhænge, og de har opstillet, fortolket og løst simple lineære ligninger algebraisk og grafisk i tilknytning til sådanne modeller. I dette arbejde har eleverne har fået erfaring med at beregne og tegne grafer for lineære sammenhænge ved hjælp af regneark og dynamisk geometri. Eleverne kan desuden for simple lineære sammenhænge bestemme parametrene for en lineær funktion ud fra konteksten, en funktionstabel eller en funktionsgraf – en ikke-lodret ret linje.
Fase 1
I grundskolen har eleverne arbejdet med lineære funktioner som samhørende variation såvel som en korrespondance mellem en uafhængig og en afhængig variabel. Det kan forventes, at eleverne kan bruge denne forståelse til modellering af simple lineære sammenhænge – både i situationer, hvor den uafhængige variable varierer diskret inden for $\mathbb{N}$ eller $\mathbb{Z}$, og inden for $\mathbb{R}$, hvor funktionen er kontinuert.
Ved starten på gymnasial uddannelse skal elevernes erfaringer og viden konsolideres, formaliseres og generaliseres. I fase 1 er der fokus på samspillet mellem funktionsbeskrivelse og trinvis beskrivelse af lineære sammenhænge samt på støtte elevernes begyndende forståelse af en lineær funktion som et matematisk objekt. Det sker ved at arbejde med alle fire repræsentationer i forhold til begge perspektiver på lineære funktioner.
Der kan tages udgangspunkt i en eller flere konkrete problemstillinger. Som det er indikeret i Overblikket, kan det fx være i relation til vandforbrug ved brusebad.
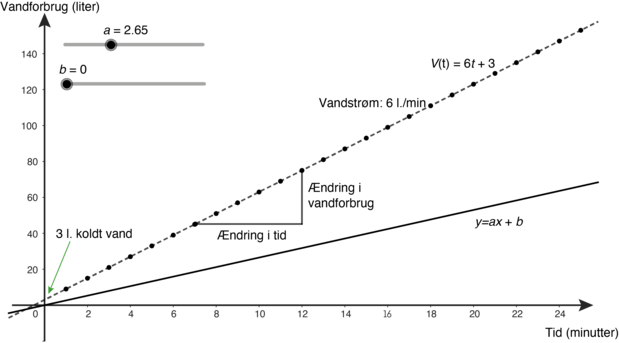
I GeoGebra kan elever formidle resultaterne af deres undersøgelser. De kan opleve og illustrere, at parameterværdier i forskriften $f(x) = a \cdot x + b$ er entydige for en given ikke-lodret linje. Der kan lige såvel arbejdes med andre kontekster. Det vigtige er, at den uafhængige variabel i konteksten kan variere kontinuert, og at konteksten giver mening for eleverne. Der kan være en pædagogisk værdi ved, at eleverne også kan undersøge nogle af de sammenhænge, der arbejdes med, gennem egne empiriske undersøgelser, selvom det naturligvis er tidskrævende. Samarbejde med andre fag kan være en mulighed.
Det er sigtet, at der udvikles en praksis i arbejdet med lineære funktioner, hvor eleverne beskriver lineære sammenhænge som funktioner og som trinvis udvikling i alle fire repræsentationsformer. Fra grundskolen har eleverne erfaring med at bruge forskriften for lineære funktioner, $f(x) = a \cdot x + b$, til at tegne grafen for funktionen, men for mange elever er det ikke klart, at punkterne på den linje, de tegner, er netop de punkter, der passer i funktionsforskriften. Det kan fremhæves for eleverne i de konkrete eksempler og generaliseres ved drøftelse af betydningen af skrivemåden, $y = f(x)$, som jo netop indkapsler funktionsegenskaben.
Parametrenes betydning er central i fase 1. De fleste elever kender til hældningskoefficienten eller hældningstallet og skæringen med 2. aksen for en ret linje og ved også, at det er henholdsvis $a$ og $b$ i ligningen for en ret linje på formen $y = a \cdot x + b$.
Det er imidlertid vigtigt at skabe sammenhæng i elevernes forståelse af parametrene i deres geometriske, algebraiske og kontekstuelle betydning. Når eleverne har arbejdet med at beskrive lineære sammenhænge med funktionsforskrifter, $f(x) = a \cdot x + b$, og trinvis udvikling med $a$ som den konstante ændring i $y$ ved en tilvækst på 1 i $x$, kan sammenhængen vises algebraisk – i først omgang netop ved en tilvækst i $x$ på 1; $f(x + 1) = a \cdot (x + 1) + b = f(x) + a \cdot 1$.
For de allerfleste elever vil det er nok være første gang, at de oplever, at man kan indsætte et algebraisk udtryk for $x$ i en funktionsforskrift; så det må naturligvis drøfte med eleverne. Resultatet kan imidlertid give mening for eleverne, fordi det kan forbindes til deres erfaringer med at beregne funktionstabeller og med tegning af rette linjer ud fra et punkt og en hældningskoefficient: ”En frem og hældningskoefficienten op eller ned alt efter fortegn”.
I modelleringssammenhænge kan eleverne fortolke og i nogle tilfælde også bestemme parametrene ud fra konteksten. Det er tydeligt i tilfældet med brusebadet. $a$ er vandflowet (6 liter/minut), da der for hvert minut, der bades, bruges 6 liter, og $b$ er startværdien, der svarer til den mængde vand (3 liter), der løber ud af bruseren, inden vandet får den rette temperatur. Eleverne kan ydermere selv ændre på vandflowet under et brusebad og tænke, at de skruer op og ned for hældningskoefficienten, mens de bader. De kan evt. slukke for vandet under hårvask, og i fase 4 kan de modellere denne situation med en stykkevis lineær funktion.
I sådanne kontekster kan det tydeliggøres for eleverne, at de variable og parametrene har enheder, der passer sammen, så $[ a ] = \frac{ [ y ]}{ [ x ] }$ og $[ b ] = [ y ]$. Det gælder generelt og kan bruges ved opstilling af lineære modeller.
I den nævnte praksis fremstiller eleverne sproglig, tabel-, algebraisk og graf-repræsentation af konkrete lineære sammenhænge. Det er vigtigt, at dette arbejde foregår i hånden. It-værktøjer kan anvendes til sammenfatning og formidling med dynamisk illustration af faglige pointer, men det må ske på grundlag af en forståelse af de centrale begreber og deres repræsentationer.
En udfordring med de autentiske kontekster er, at de typisk alene giver mening for ikke-negative værdier af de variable – og oftest også af parametrene. Derfor er der brug for allerede i fase 1 at arbejde med lineære funktioner også i rent matematiske sammenhænge.
Elevernes praksis med at beskrive konkrete lineære sammenhænge kan sammenfattes og generaliseres ved, at de får til opgave at lave et regneark, hvor man frit kan indsætte værdier af parametrene $a$ og $b$ og beregne den lineære sammenhæng trinvist og med funktionsforskriften $f(x) = a \cdot x + b$. Det er en pointe, at eleverne selv skal udvikle regnearket, så man også kan variere på tilvæksten i den uafhængige variabel. Eleverne kan efterfølgende få til opgave at finde lineære funktioner, der netop ikke ”kommer” i hver af de fire kvadranter. En sådan opgave sikrer, at eleverne kommer til at arbejde med alle mulige kombinationer af fortegn for parametrene i forskriften for en lineær funktion. De særlige tilfælde, hvor enten en af $a$ eller $b$ er nul, eller både $a$ og $b$ er nul, må ligeledes behandles eksplicit. Også identiteten $f(x) = x$ fortjener særlig opmærksomhed. Fra matematikdidaktisk forskning ved man, at elevernes mentale billede af et matematisk begreb, fx lineær funktion, udspændes af de eksempler, som de konkret har arbejdet med. Det gælder uanset, hvor omhyggeligt begrebet er defineret over for eleverne. Det er derfor vigtigt, at eksemplerne udspænder muligheder.

Fase 2
I fase 2 kan sammenhængen mellem trinvis og funktionsbeskrivelse af lineære sammenhænge formaliseres yderligere. Formlen for hældningskoefficienten ud fra to punkter på en linje kan udledes. Den har eleverne mødt og brugt i grundskolen, men nok de færreste har forstået dens grundlag. Elevernes oplevelse fra fase 1 af, at tilvæksten i den afhængige variabel er a gange tilvæksten i den uafhængige variabel, giver et godt grundlag for at følge udledningen af sammenhængen algebraisk.
For en lineær funktion $f(x) = a \cdot x + b$ gælder:
$f(x + \Delta x) = a \cdot (x + \Delta x) + b = f(x) + a \cdot \Delta x \Leftrightarrow a = \frac{f (x + \Delta x) - f(x)}{\Delta x} , \Delta x \neq 0$
Med $x_1 = x$ og $x_2 = x + \Delta x$ samt at $y_1 = f(x_1)$ og $y_2 = f(x_2)$ giver det formlen:
$a = \frac{y_2-y_1}{x_2-x_1}$ og/eller $a = \frac{\Delta y}{\Delta x}$
til bestemmelse af parameteren $a$ i forskriften i en lineær funktion og hældningskoefficienten for den tilhørende rette linje. $b$ kan bestemmes ved indsættelse af $a$ og et punkt i forskriften. Dermed er en lineær funktion entydigt fastlagt ved to punkter, der passer i funktionen. Det er værd at fremhæve for eleverne.
Det er nok ikke almindeligt i gymnasial undervisning at forankre elevernes forståelse af hældningskoefficienten i elevernes erfaringer med trinvis beskrivelse af lineære funktioner. Det giver imidlertid mulighed for at støtte elevernes begrebsforståelse gennem en gradvis udvikling af deres praksis med trinvis og funktionsbeskrivelse af lineære funktioner, som beskrevet i fase 1. Samtidig giver det et godt grundlag for senere forståelse af differentialregning.
Udledningen af formlen for hældningskoefficienten ved indsættelse af to punkter, der passer i forskriften, bør naturligvis også behandles. Det kan være som anvendelse af metoder til løsning af to ligninger med to ubekendte. Begge udledninger rummer uden tvivl algebraiske udfordringer for eleverne. Det gælder indsættelse af $x + \Delta x$ i forskriften for en lineær funktion; henholdsvis skiftet fra $x$ og $y$ som variabel til at opfatte $a$ og $b$ som ubekendte. Selve løsningen ved substitution eller ved at trække ligningerne fra hinanden kan også volde udfordringer. Tilsammen kan metoderne støtte elevernes forståelse af centrale aspekter ved lineære funktioner, parameteren $a$ og hældningskoefficienten for en ret linje. Eleverne skulle gerne nå dertil, at de ikke behøver at huske den såkaldte ”to-punktsformel” til bestemmelse af $a$, men at de kan basere sig på forståelse af dens betydning i forskriften for en lineær funktion og som hældningskoefficient for en ret linje.
Der opereres på forskellige måder med forskriften for en lineær funktion, og det kan støtte, at eleverne begynder at opfatte en lineær funktion som et matematisk objekt. Drøftelse med eleverne af styrker og udfordringer ved de to udledninger kan desuden bidrage til, at de oplever betydningen af at kunne benytte algebra.

Fase 3
Her er der fokus på at styrke og udbygge elevernes matematiske forståelse af lineære funktioner og deres grafer som ikke-lodrette linjer samt at styrke deres forståelse af rette linjer som punktmængder. Der arbejdes fortsat med udvikling af elevernes praksis med brug af de fire repræsentationer, men fokus er især på omformning og fortolkning af algebraiske repræsentationer. De matematiske erkendelser, der opnås herved, kan støttes og fastholdes som fælles læring i klassen ved hjælp af dynamiske undersøgelser og illustrationer i GeoGebra.
Arbejdet med at bestemme en ligning for en ikke-lodret ret linje ud fra et punkt på linjen og en given hældning kan styrke elevernes forståelse af en ret linje som et matematisk objekt, der kan karakteriseres på forskellige måder. For de fleste elever er det nok ikke indlysende, at en linje og dermed en lineær funktion er fastlagt entydigt ud fra et punkt og en given hældning. Det kan der arbejdes med i konkrete tilfælde, og på grundlag heraf kan den generelle sammenhæng behandles algebraisk og anvendes ved arbejdet med stykkevis lineære funktioner.
For at skabe sammenhæng til arbejdet med hældningskoefficienten i fase 2 kan man se på en ret linje gennem et givet punkt $(x_0,y_0)$ og med en given hældning, $a$. Fra fase 2 ved eleverne, at denne hældning kan findes ud fra to punkter på linjen. Men da linjen har samme hældning overalt, må det gælde, at ethvert andet punkt på linjen $(x, y)$ danner hældningen $a$ med $(x_0,y_0)$. Det giver:
$a = \frac{y - y_0}{x - x_0} \Rightarrow y - y_0 = a \cdot (x - x_0) \Rightarrow y = a \cdot (x - x_0) + y_0 \Rightarrow$
$y = a \cdot x - a \cdot x_0 + y_0, \ \text{hvilket er det samme som} \ y = a \cdot x + b, \ \text{med} \ b = y_0 - a \cdot x_0$
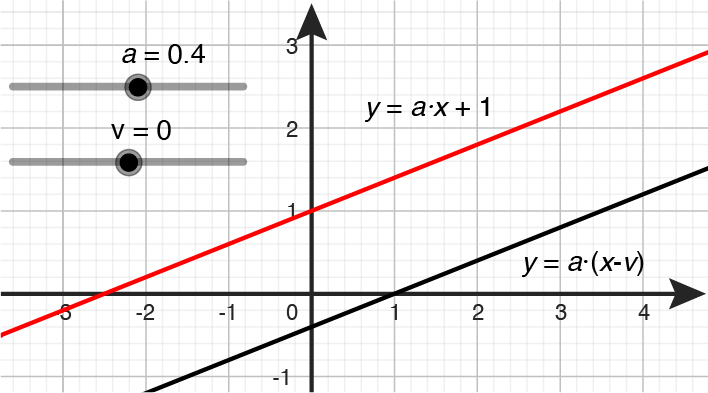
Eleverne kan – evt. i grupper – arbejde med at illustrere ligningen $y = a \cdot (x - x_0) + y_0$ i GeoGebra (som vist til højre). I templaten kan man få tegnet en ret linje med en hældning, der kan varieres med en skyder, og som går gennem et punkt, man frit kan placere.
Ligningen $y = a \cdot (x - x_0) + y_0$ er relevant, fx som ligningen for en tangent. Samtidig kan den fortolkes som, at linjen med ligningen $y = a \cdot x$, der jo går gennem $(0,0)$, er vandret parallelforskudt mod højre med $x_0$ og lodret parallelforskudt med $y_0$, således at den går gennem $(x_0, y_0)$.
Der kan arbejdes med lodret og vandret forskydning af lineære funktioner (rette linjer) ved hjælp af GeoGebra, og eleverne kan opleve, at parallelle rette linjer kan opfattes som enten lodret eller vandret parallelforskudt.
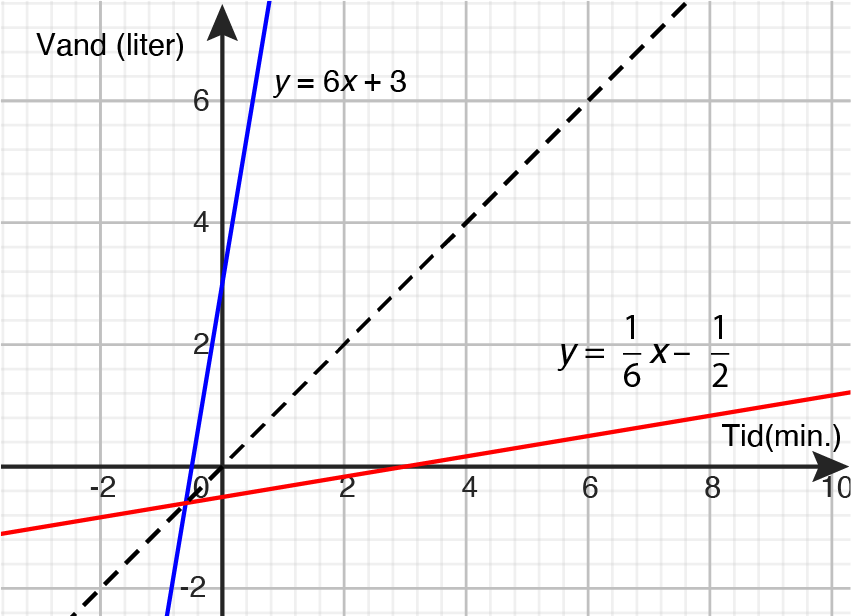
I fase 3 arbejdes med at bestemme den omvendte funktion til en ikke-konstant lineær funktion. Det kan ske med afsæt i brusebadet. Opgaven er nu at opstille en model for, hvor lang tid man kan bade, $B(v)$, som funktion af, hvor meget vand, $v$, man må bruge. Det kan evt. foregå i grupper, og som støtte kan eleverne i første omgang opstille en tabel, der angiver sammenhængen. Eleverne opdager nok hurtigt, at tabellen fra tidligere også angiver badetiden som funktion af vandmængden. Men det er sikkert udfordrende for mange at nå frem til en forskrift for badetiden. Eleverne har metoder til at bestemme forskriften for en lineær funktion ud fra to punkter fra fase 2, men iværksættelse heraf forudsætter, at eleverne indser, at det en lineær funktion, de skal finde.
Det vil være udtryk for god forståelse, hvis nogle grupper selv finder på at isolere $t$ i forskriften af $V(t): v = 6 \cdot t + 3 \Rightarrow t = \frac{v - 3}{6}$ og når frem til, at $B(v) = 0,167 \cdot v - 0,5$ er en lineær funktion, der angiver badetiden som funktion af vandmængden.
Efterfølgende kan der arbejdes med bestemmelse af den omvendte funktion til en ikke-konstant lineær funktion generelt ved hjælp af algebra, og det kan drøftes med eleverne, hvorfor konstante funktioner ikke har en omvendt funktion. Ligeledes kan der arbejdes med sammenhængen mellem en lineær funktion og dens omvendte i grafrepræsentation. Graferne spejler hinanden i linjen $y = x$, og funktionen $f(x) = x$ (identiteten) er sin egen omvendte. For alle ikke-konstante lineære funktioner, hvor $a \neq 1$, er der netop ét punkt, der er fælles for funktionen og dens omvendte. Det er linjernes skæringspunkt, som også ligger på $y = x$. Det er samtidig et fixpunkt for begge de lineære afbildninger, der er i spil.
Endelig kan elever arbejde med sammensætning af en lineær funktion med dens omvendte i konkrete situationer og opleve, at det giver identiteten. Ved brusebadet kan det give mening for eleverne, at hvis udtrykket for vandforbruget ved badning i $t$ minutter, $6t +3$, indsættes for $v$ i funktionen for badetiden, så giver det:
$B(v) = 0,167 \cdot (6t +3) - 0,5 = t$
Sammenhængen kan behandles generelt i både graf og algebraisk repræsentation.

Som afrunding på fase 3 arbejdes med at beskrive punktmængder, der danner rette linjer i planen, og med linjens ligning på normalform, $c \cdot x + d \cdot y = e$ med $c, d$ og $e$ som reelle konstanter. Eleverne kan selv indse sammenhængen til ligningen for ikke-lodrette linjer, $y = ax + b$, når $d \neq 0$, og at ligningen $c \cdot x + d \cdot y = e$ for $d = 0$ netop repræsenter lodrette linjer.
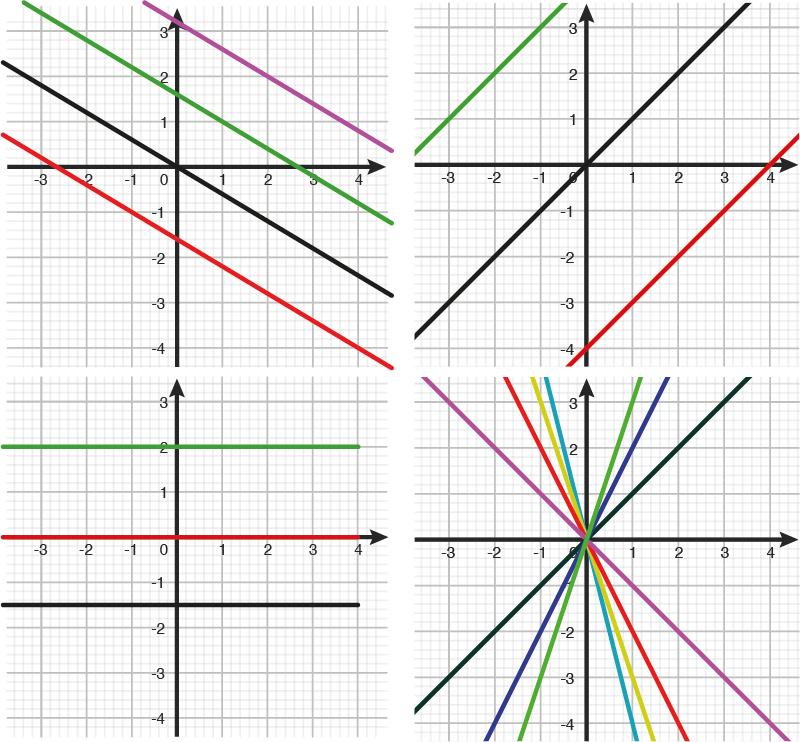
Med udgangspunkt i sproglige beskrivelser af punktmængder, der danner rette linjer, kan eleverne arbejde med at opstille ligninger på normalform og tegne tilhørende grafer. Nogle muligheder kunne være:
- Linje med hældningen $2$ gennem $(0,-1)$.
- Linje med hældningen $-\frac{1}{2}$, der går gennem $(2,3)$.
- Linje gennem $(5,3)$ og $(5,-3)$.
- Vandret linje gennem $(5, 3)$.
- 1.aksen.
- 2. aksen.
Punkter med koordinatsummen 10; Punkter hvor x-koordinaten er 2 større end y-koordinaten; og Punkter hvor x-koordinaten er dobbelt så stor som y-koordinaten minus 2.
Der kan også arbejdes med at beskrive forskellige familier af rette linjer med udgangspunkt i sproglige beskrivelser eller grafrepræsentationer som illustreret.
I fase 4 i læringssporet ”At løse ligninger” er løsning af to lineære ligninger på normalform behandlet. I nærværende spor kan det (igen) tydeliggøres for eleverne, at der er tre løsningstilfælde: De linjer, ligningerne repræsenterer, er (1) ikke-parallelle og har netop ét skæringspunkt, $x$ og $y$ er entydigt bestemt, (2) sammenfaldende, så alle punkter på linjen er løsninger til ligningerne, og (3) parallel og ikke-sammenfaldende, hvorfor der ingen løsninger er til ligningerne.
Fælles for alle aktiviteter i fase 3 er, at de sigter mod at støtte elevernes forståelse af lineære funktioner og rette linjer som matematiske objekter samt deres forståelse af den entydige sammenhæng mellem lineære funktioner og ikke-lodrette linjer.
Fase 4
I fase 4 skifter perspektivet på arbejdet med de lineære modeller. Hvor de tidligere faser har tjent til at motivere og give mening til begreber og metoder, er sigtet nu, at eleverne bringer deres forståelse af lineære funktioner i spil ved opstilling og analyse af matematiske modeller. Det sker med henblik på at styrke elevernes modelleringskompetence. Det indebærer brug af såvel funktionsbeskrivelse som trinvis beskrivelse af lineære sammenhænge til opstilling og analyse af modeller. Eleverne arbejder med at opstille, analysere og vurdere lineære modeller ud fra målte eller givne data ved hjælp af lineær regression. Der er gode argumenter for at lade eleverne gennemføre eksperimenter eller anden form for dataindsamling som led i deres modelleringsarbejde, selvom det er tidskrævende. Det bidrager til at forankre elevernes modelleringsarbejde i konkrete oplevelser.
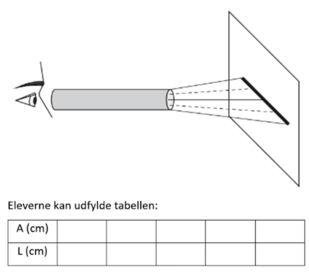
Et simpelt forsøg, som mindre grupper let kan udføre i klassen, er det såkaldte kikkertforsøg. Eleverne skal finde og beskrive sammenhængen mellem afstanden fra en kikkert til en væg og længden af det vandrette linjestykke, der kan ses gennem kikkerten, når den rettes vinkelret mod væggen. Et stykke malertape på fx 1 m kan sættes på væggen, så det synlige linjestykke kan markeres og måles. Som kikkert kan bruges en toiletpapirsrulle eller en køkkenrulle. Sammenhængen kan bestemmes både empirisk, evt. ved anvendelse af lineær regression, og geometrisk, og parametrene for den lineære funktion kan fortolkes og forstås i forhold til diameteren og længden af kikkerten.
Afkøling (af fx kakao) er et andet eksempel på en problemstilling, som eleverne kan forstå og selv undersøge ved hjælp af enkle målinger. Det kan ske med udstyr, der findes i mange hjem, eller ved, at målingerne gennemføres på skolen i et faglokale. Udgangspunktet for elevernes arbejde kan være spørgsmålet:
Hvordan ændrer temperaturen af kakaoen sig, efter den er trukket i automaten i kantinen på skole?
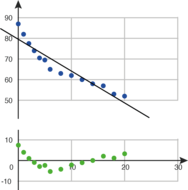
Hvis temperaturen måles hvert 2. minut i 20 minutter, så kan eleverne i regneark beregne en trinvis lineær udvikling med udgangspunkt i starttemperaturen og a som en parameter, der angiver, hvor mange grader temperaturen ændrer sig per minut. De kan justere værdien af $a$, så linjen passer godt til data.
Efterfølgende kan den bedste rette linje bestemmes ved hjælp af lineær regression i et it-værktøj. Eleverne kan sammenligne og vurdere de to lineære modeller fx i forhold til starttemperaturens betydning. Eleverne må udfordres til at overveje, om en lineær model i det hele taget giver en god beskrivelse af temperaturens udvikling på sigt. Visuel inspektion – eventuelt støttet af et residualplot – afslører en systematik i afvigelserne mellem regressionslinjen og data. I de lineære modeller bliver temperaturen ved med at falde med det samme per minut – så kakaoen bliver til is i modellen. Det må føre til en afvisning af en lineær sammenhæng mellem tid og temperatur som en god model for afkøling (af kakao).
Hvis temperaturen af omgivelserne også måles, er der grundlag for at udvikle en bedre model. En antagelse om, at temperaturen falder proportionelt med forskellen mellem kakaoens og omgivelsernes temperatur – i stedet for at falde med det samme antal grader – kan faktisk relativt let matematiseres i elevernes regnearksmodel for den trinvise udvikling.
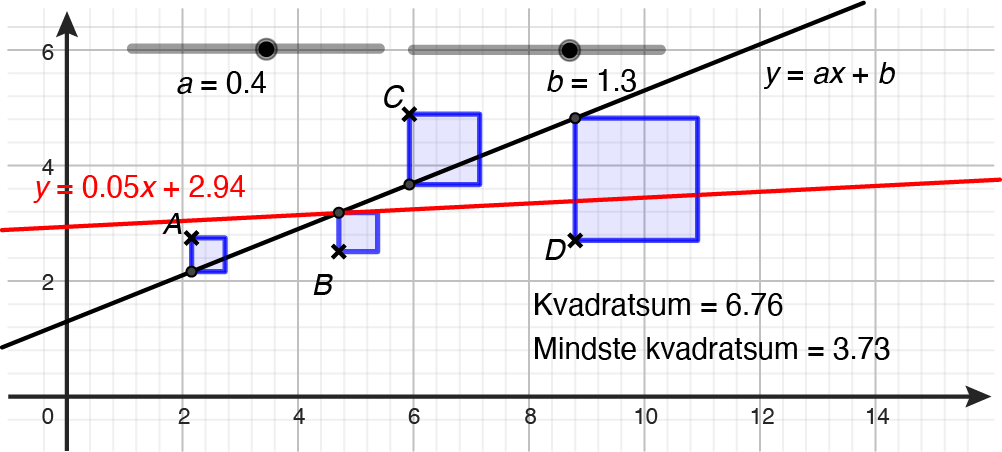
I grundforløbet introduceres brugen af lineær regression til bestemmelse af den bedste linje gennem en given mængde af datapunkter. Nogle elever kender til metoden fra grundskolen, men det drøftes typisk ikke med eleverne, hvad ”den bedste linje” betyder i denne sammenhæng. Det er heller ikke muligt eller hensigtsmæssigt på dette tidspunkt at forklare, hvordan metoden virker. Det kan imidlertid godt give mening at drøfte og illustrere princippet bag lineær regression ved hjælp af mindste kvadraters metode. Det kan gøres i GeoGebra, ved at eleverne selv kan fitte en linje til få givne datapunkter ved at forsøge at minimere summen af kvadraterne på afvigelserne mellem datapunkterne og deres bud på en linje.
I fase 4 kan modellen af brusebadet udvides til en model for brusebad med hårvask og brug af balsam – hvorfor der slukkes for vandet i periode. Det kan ske ved hjælp af en stykkevis lineær funktion. Elevernes ejerskab til modellen styrkes, ved at de selv bestemmer, hvornår og hvor længe der slukkes for vandet. Hermed opstår der et behov for at kunne variere vandstrømmen i modellen. I regnearksrepræsentationen af den trinvise beregning af vandforbruget er det intuitivt for mange elever, hvordan der kan slukkes for vandet i modellen. Den trinvise udvikling skal blot sættes på pause og vandforbruget holdes konstant, så længe der er slukket. Formlen for den trinvise fremskrivning virker, så snart der igen lukkes op for vandet. Opstilling af en tilsvarende stykkevis lineær funktion er lidt mere krævende. Mens der er slukket, holdes vandforbruget konstant, men når der åbnes for vandet, er det ikke længere den samme funktion, der beskriver vandforbruget. Vandstrømmen er den samme, men der er nu sket en forskydning – lodret eller vandret, alt efter hvordan man ser det. Modelleringskonteksten udfordrer og giver mening til elevernes manipulation med lineære funktioner og bidrager herved til deres begrebsforståelse.
Det skal understreges, at der naturligvis kan arbejdes med mange andre kontekster for modellering og problemløsning ved hjælp af lineære funktioner, end dem der er behandlet i sporet. Det er naturligvis også en mulighed at udfordre eleverne – evt. i grupper – til selv at finde, beskrive og analysere eksempler på lineære modeller. De 17 verdensmål rummer fx flere eksempler på, at (stykkevis) lineære funktioner bliver brugt eller kan bruges til beskrivelse af en tidslig udvikling eller andre sammenhænge.


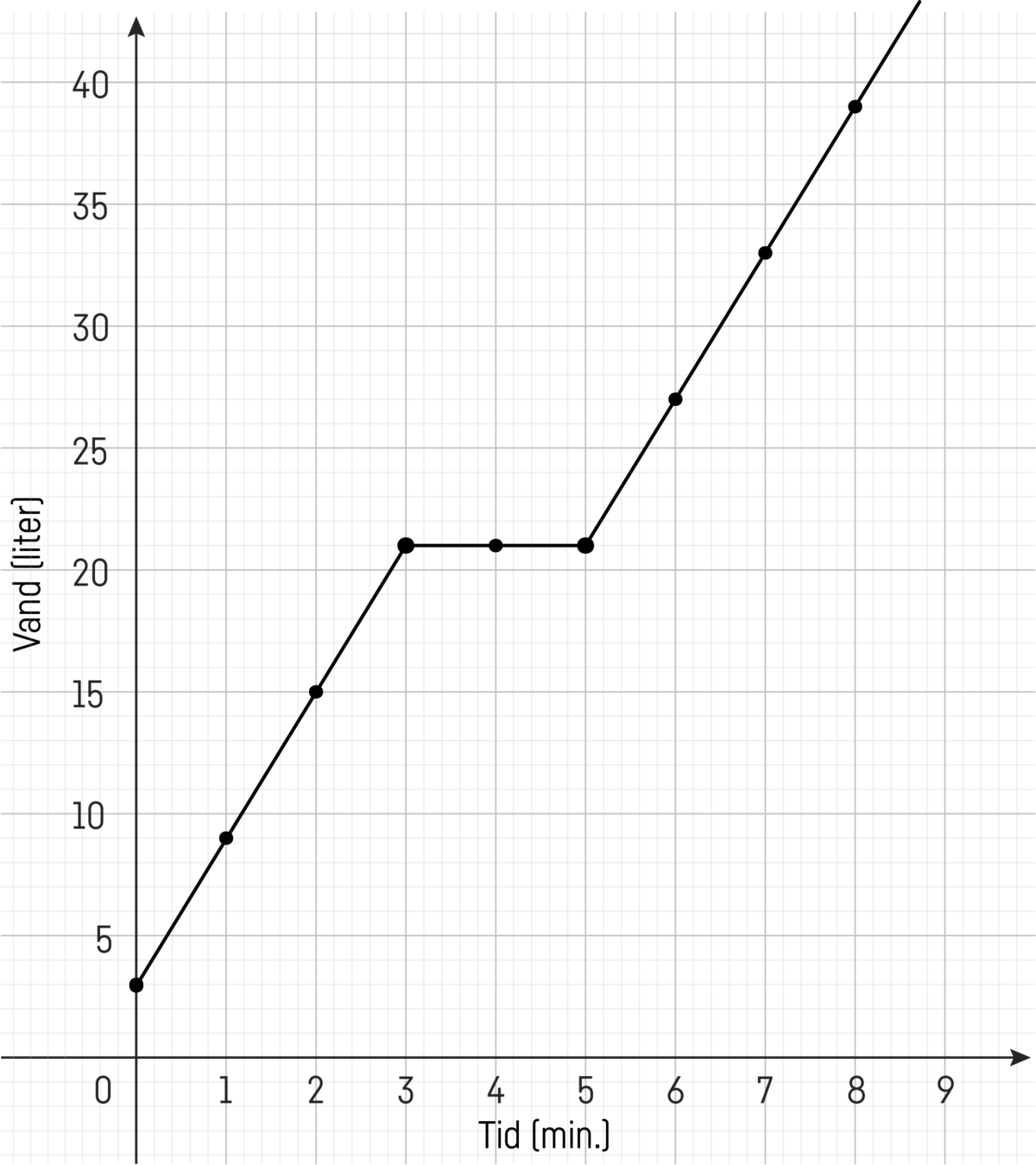
Trinvis beskrivelse:
$V(0)=3 l. \quad V(t+\Delta t)=V(t)+\Delta V$
$\Delta V = \begin{cases} 6\Delta t & for \ 0 \leq t \leq 3\\ 0 & for \ 3 < t \leq 5\\ 6\Delta t & for \ 5 < t \end{cases}$