Teoretiske perspektiver på læring af lineære funktioner
Det spørgsmål som teksten søger at give svar på er:
Hvordan kan jeg, som matematiklærer, forankre og styrke elevers forståelse af lineære funktioner?
Funktioner - et centralt matematisk begreb
Funktionsbegrebet er et af de matematiske emner, der er forsket og forskes mest i (Thompson & Carlson, 2017). Det er der flere grunde til.
En grund er, at funktioner er et centralt matematisk begreb, der er afgørende for læring og anvendelse af matematik på både grundskolens mellem- og sluttrin samt gymnasialt niveau, hvor det indgår i grundlaget for differential- og integralregning. Desuden anvendes funktioner, ikke mindst lineære funktioner, udbredt i andre fag og praksisområder. En rodfæstet forståelse af funktionsbegrebet er derfor en forudsætning for en matematikbaseret videregående uddannelse og for mange erhverv.
En anden grund er, at mange elever har svært ved at forstå funktioner, også lineære, og navnlig at bruge dem i forbindelse med problembehandling og modellering. Det ses på de ældste klassetrin, men særlig markant ses det ved starten på den gymnasiale matematikundervisning. Det er bl.a. derfor, at lineære funktioner er udvalgt som fokus i gymnasiets grundforløb (se rapport om grundforløbet på emu.dk).
En tredje grund er, at flere principielle vanskeligheder ved læring af matematiske begreber træder tydeligt frem ved introduktion af funktionsbegrebet. Her møder elever første gang formalisering af sammenhængen mellem to variable, hvor det især er brugen af algebra i form af ligninger med to variable, som volder vanskeligheder. Men der er i det hele taget udfordringer i arbejdet med og samspillet mellem de forskellige repræsentationsformer for funktioner, såsom sprog, tabel, algebra, graf og algoritme/program (Ayalon, M., & Wilkie, K., 2020).
Hvorfor er det vanskeligt at forstå funktioner?
Det er en generel erkendelsesteoretisk udfordring ved læring af matematiske begreber, at vi kun har adgang til begreberne via repræsentationer af dem. Matematiske begreber er ikke en del af vores omverden i form af konkrete materielle objekter. Oftest ses de som kulturelt udviklede objekter og mentale konstruktioner. Dette forhold er grundigt belyst i matematikdidaktisk forskning, bl.a. af den tyske matematikdidaktiker Steinbring (se fx Steinbring, 2005).
Steinbring har videreudviklet en såkaldt erkendelsesteoretisk trekant, der er udspændt af repræsentation, objekt og begreb. Repræsentation er en symbolsk repræsentation af begrebet i et notationssystem, fx algebra, tabel, graf, mens objekt henviser til en anvendelse af begrebet. Pointen er, at det er via relationerne mellem objektet og forskellige repræsentationer, at eleverne kan få fat i begrebets betydninger. Og problemet er, at der i undervisning ofte ikke bliver etableret et selvstændigt objekt, som eleverne kan forholde sig til, og som repræsentationerne af begrebet kan henvise til. Dette gælder særligt ift. lineære funktioner i både grundskolen og gymnasiet, hvor de objekter, der arbejdes med, ofte bliver identiske med deres algebraiske repræsentationer, dvs. f(x) = ax+b for en lineær funktion og ligningen y = ax+b for en ret linje.
Som lærer er det naturligt at fokusere opmærksomheden på de algebraiske repræsentationer, fordi de er bærende for fremstillingen i lærebøgerne, og fordi mange elever i særlig grad oplever vanskeligheder med denne repræsentationsform.
Imidlertid peger Steinbring på, at algebraiske repræsentationer først bliver meningsfulde for elever, når de anvendes til at beskrive og undersøge objekter, der indgår i anvendelsessammenhænge eller andre kontekster, som er meningsfulde for elever. Det kan fx ske gennem et arbejde med matematisk modellering, hvor udgangspunktet er fænomener og problemstilling (objekt), som eleverne kan beskrive og undersøge ved hjælp af lineære funktioner. Her kan de algebraiske repræsentationer få mening og vise deres styrke for eleverne, samtidig med at eleverne i denne proces kan udvikle deres forståelse af lineære funktioner som begreb. Her er der altså tale om at bruge modellering som didaktisk middel til at styrke elevernes begrebsforståelse (Blomhøj, M., 2019).
Modeller for dannelse af matematiske begreber
Ved læring af matematiske begreber spiller dualiteten mellem at forstå et begreb som henholdsvis en proces og et objekt ofte en afgørende rolle. Dette gælder ikke mindst for funktionsbegrebet. Der er udviklet forskellige teorier for og modeller af, hvordan en sådan begrebsudvikling kan foregå.
Her eksemplificerer vi en model udviklet af Anna Sfard (1991) med fokus på dannelse af et funktionsbegreb. Modellen består af tre faser. I den første fase (kaldet interiorization) internaliserer eleven en proces, som udføres på allerede velkendte objekter (fx heltal). Det kan fx være, at eleven kender de første par af talværdier af to variable og skal bestemme de næste værdier af den ene ud fra værdier af den anden. Efterhånden kan eleven tale om processen uden at udføre den konkret. Eleven kan således se for sig, at man kan finde disse sammenhørende værdier, og at man kan repræsentere resultatet i en tabel eller som en graf. I anden fase (condensation) kondenserer eleven processen til et mere kompakt og samlet hele og kan her arbejde med forskellige repræsentationer af denne sammenhæng. I tredje fase (reification), hvortil det kræver et kognitivt spring at nå, kan eleven opfatte denne nye helhed som et selvstændigt objekt. Eleven ser nu funktioner som et objekt med bestemte egenskaber, der kan indgå i nye processer, som fx regning med funktioner. Uden den sidste krævende fase vil eleven alene kunne udføre operationerne. En fuldt udviklet begrebsforståelse indebærer, at eleven fleksibelt kan skifte mellem en proces og objektforståelse af en funktion.
Udover at afdække vanskeligheder ved elevers læring af funktionsbegrebet og at udvikle modeller herfor så har matematikdidaktisk forskning også undersøgt og udviklet teorier, der belyser mulighederne for og styrkerne ved at forankre elevernes begrebsforståelse i deres erfaringsverden og i konkrete oplevelser (altså det Steinbring kalder objekter) med matematisk modellering.
Det gælder bl.a. den hollandske skole Realistic Mathematics Education (RME). I RME arbejder elever i første omgang med at udvikle matematiske beskrivelser af velkendte ikke-matematiske fænomener, fx ved at udvikle en beskrivelse af et konkret fænomen som fx antal lommepenge, vha. en lineær funktion med konkrete værdier. Derved udvikler elever modeller af konkrete fænomener gennem en såkaldt horisontal matematisering. I anden omgang kan eleverne så gradvist ændre perspektiv ved at arbejde med modellerne inden for matematikken. Herved løsrives modellerne fra de konkrete situationer og kan bruges til at beskrive en bredere klasse af situationer, som fx fænomener med konstant vækst. Igennem en sådan vertical matematisering bliver de oprindelige modeller af et konkret fænomen til modeller for en klasse af sådanne fænomener. Via disse to former for matematisering kan eleverne udvikle solide forståelser af de involverede matematiske begreber (Gravemeijer, 2007, 1999).
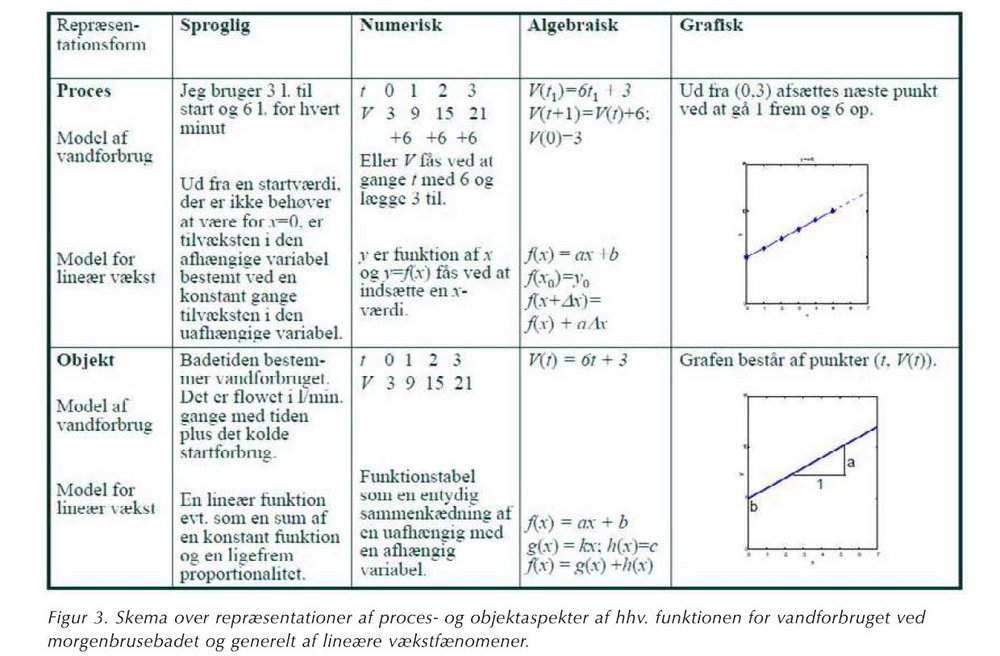
Sfards model for begrebsdannelse og RMEs termer om model af og model for kan kombineres med Steinbrings betoning af betydningen af repræsentationsformer. Det har vi gjort for lineære funktioner i figur 3.
Modellering som middel til at udvikle elevernes begrebsforståelse
Morgenbrusebadet, som vist i eksemplet nedenfor, er et eksempel på, hvordan en dagligdagssituation kan beskrives og analyseres ved hjælp af matematisk modellering og give anledning til en konkret lineær funktion. Eksemplet stammer fra forløbet MatematikMorgener (Blomhøj & Skånstrøm, 2006 - Se nedenfor). Det har siden været anvendt i en række forsknings-og udviklingsprojekter.
I dette eksempel kan elever i fx 8. klasse arbejde med at opstille en model af vandforbruget ved brusebad via horisontal matematisering. Det kan de gøre ved at beskrive deres eget morgenbrusebad med måling af det kolde startforbrug og af vandstrømmen, når der er skruet op for vandet. De kan starte med at repræsentere vandforbruget i en tabel fx i et regneark, hvor der minut for minut beregnes, hvor mange liter vand der er brugt.
Regnearket bliver herved en femte repræsentationsform ift. figur 3, som integrerer et regneudtryk og en tabel (evt. en graf), og som kan gøres dynamisk ift. ændringer af startforbrug og vandstrømmen. Ud fra tabellen kan eleverne konstruere en grafisk repræsentation af vandforbruget som funktion af badetiden t (den stiplede linje i figur 2). I princippet er t kontinuert, da man jo kan slukke for bruseren, hvornår det skal være. Man kan tilnærme dette i tabellen/regnearket ved at ind føre en ny parameter, så den næste tidsværdi beregnes ved t+∆t, således at ∆t kan gøres så lille, at punkterne ligger så tæt det skal være. Beregningen af den trinvise tilvækst i vandforbruget skal så ændres til 6∆t.
Herved kan grafen - i princippet - blive til et fuldt optrukket linjestykke. Som model af brusebadets vandforbrug er funktionen kun relevant i et begrænset tidsinterval fx [0,10] minutter. Som en dreng bemærkede: "Så lang tid bader jeg ikke - efter 5 minutter er der ikke mere varmt vand, når jeg kommer efter min store søster!". Som model af vandforbruget giver eksemplet mulighed for, at eleverne arbejder med fem forskellige repræsentationsformer af dette forbrug. Hvad angår den sproglige repræsentation kan eleverne beskrive deres normale brusebad i forhold til badetid og hårvask m.v. Der opstår typisk spørgsmål om, hvad der sker, hvis man slukker for vandet under hårvask. Mange elever udvikler selv en numerisk beskrivelse af den trinvise udvikling, som de med forskellig grad af støtte kan omsætte til en formel i et regneark.
Når der i regnearket er lavet en tabel og tegnet en graf for vandforbruget over tid, kan eleverne udfordres til at beskrive sammenhængen mellem de to variable algebraisk. Ud fra elevernes arbejde kan deres forslag til funktionsudtryk drøftes i klassen for at støtte deres opfattelse af en funktion for vandforbruget som et matematisk objekt jf. Sfards model. Den algebraiske repræsentation sammenfatter jo, hvad de har fundet ud af, og egner sig godt til kommunikation derhjemme om, hvad sammenhængen er mellem badetid og vandforbrug. Ved at sammenligne deres modeller af deres vandforbrug kan eleverne erfare, at flere forskellige modeller kan bruges til at beskrive det samme fænomen. Her bliver det vigtigt at drage deres opmærksomhed mod ligheder mellem deres modeller, karakteristika ved fænomenet og ikke mindst sammenhænge mellem modeller og fænomen. På den måde kan eleverne støttes til at indse, hvilke dele af modellen der beskriver hvilke dele af fænomenet, og til at frigøre sig fra selve brusebadssituationen. Herved får de grundlag for at tale om og at forstå y = ax + b som model for denne type af vækstfænomener. Dette kan evt. understøttes af mindre tilsvarende modelleringsarbejder.
Via vertikal matematisering kan eleverne dernæst undersøge betydningen af a og b i den grafiske repræsentation i fx GeoGebra og dermed erfare, at a beskriver hældningen af den rette linje og b skæring med y-aksen, og at der er en entydig sammenhæng mellem en given ret linje og et sæt af værdier for a og b. Herved kan de udvikle deres forståelse af lineære funktioner som et objekt med bestemte egenskaber.
Ud fra modeller af vandforbruget kan der knyttes an til andre typer af funktioner og deres egenskaber. Man kan fx bede eleverne overveje, hvad der sker, hvis man skruer ned/op for vandet eller skifter ti I en sparebruser. Som en elev bemærkede: "Jeg kan skrue op og ned for hældningskoefficienten under badet, men så passer beregningen ikke mere". Dette kan give anledning til at arbejde med stykvis lineære funktioner ved fx at udfordre eleverne til at konstruere grafer for og lave beregninger af vandforbruget, hvor der slukkes for vandet under hårvask og måske igen ved brug af hårbalsam. Eleverne kan endvidere arbejde med at bestemme det samlede vandforbrug, når de vasker hår eller bruger balsam ud fra grafer, der viser vandstrømmen som funktion af badetiden. Herved skabes grundlag for, at modeller af vandforbruget også kan understøtte elevernes begyndende forståelse af integration.
Vi fremhæver brusebadet som en eksemplarisk aktivitet af tre grunde. For det første giver den mulighed for, at elever kan lave modeller af et konkret, velkendt og ikke-matematisk fænomen, som de senere kan generalisere til modeller for tilsvarende typer af fænomener. Dette arbejde involverer elever i de to vigtige processer: vertikal og horisontal matematisering. For det andet giver aktiviteten mulighed for, at elever kan udvikle en bred forståelse af lineære funktioner som begreb, fordi de kan arbejde med relationerne mellem objektet (altså vandforbruget ved et brusebad) og forskellige repræsentationer af forbruget, jf. Steinbrings erkendelsesteoretiske trekant. For det tredje kan elever støttes til at gå fra at regne på vandforbruget og lave beskrivelser af det til at tænke på vandforbrugsfunktionen som et objekt, der kan repræsenteres på forskellige måder og indgå i andre processer. Aktiviteten kan altså, ifølge Sfard, støtte elever i at udvikle en dualitetsforståelse af den lineære funktion som både en proces og et objekt, jf. figur 3.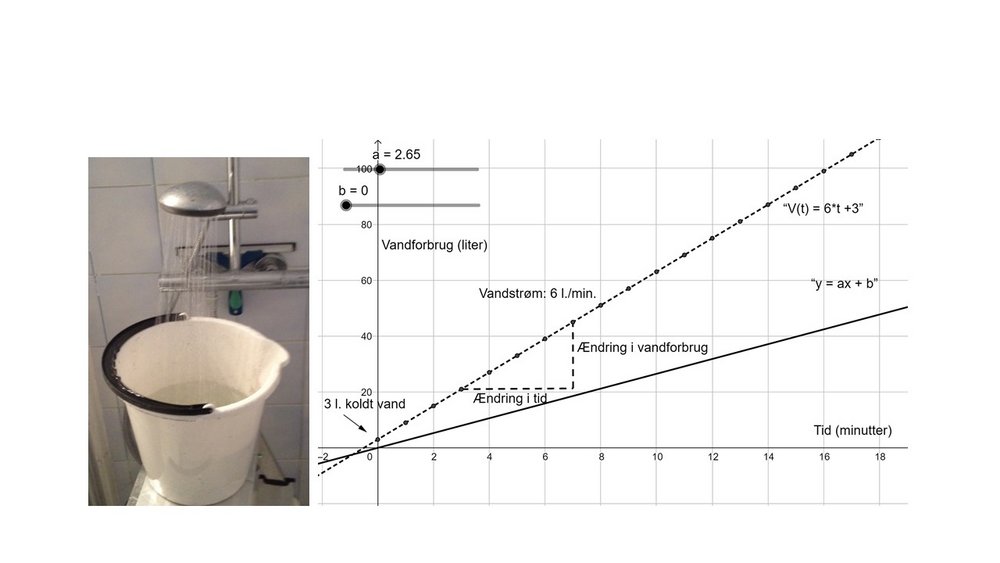
Figur 2. Fra model af morgenbrusebadet til model for lineære vækst fænomener (Blomhøj, 2019, side 44).
d. 19.01.2021
Forfattere
Charlotte Krog Skott
Docent
Københavns Professionshøjskole
Morten Blomhøj
Professor
DPU, Aarhus Universitet
Uddrag fra tidsskriftet MATEMATIK
Artiklen her er et let revideret uddrag af artiklen: 'NCUM - Nationalt Center for Udvikling af Matematikundervisning'. Der udkom i november-udgaven af tidskriftet MATEMATIK 2020. I artiklen præsenteres mål, visioner og opgaver i NCUM.
Som eksempel på hvordan matematikdidaktisk forskning kan bidrage til udvikling af undervisningspraksis, skriver forfatterne om emnet lineære funktioner på mellem- og sluttrin.
Uddraget her er en smagsprøve på NCUMs formidling af matematikdidaktisk forskning til brug for udvikling af undervisningspraksis præsenteres.
Se hele artiklen her (pdf)
Artiklens referencer
- Ayalon, M., & Wilkie, K. (2020). Students’ identification and expression of relations between variables in linear functions tasks in three curriculum contexts. Mathematical Thinking and Learning, 22(1), 1-22.
- Blomhøj, M., (2019). Towards integration of Modelling in secondary mathematics teaching. In G. Stillman & J. Brown (eds.) Lines of inquiry in Mathematical modelling research in education, 37-51. Switzerland: Springer.
- Blomhøj, M & Skånstrøm, M. (2006). Matematik Morgener - matematisk modellering i praksis. I 0. Skovsmose og M. Blomhøj (red.) Kunne det tænkes? - om matematiklæring. København: Malling Beck, 7-23.
- Gravemejier, K. (2007). Emergent modeiling as a precursor to mathematical modeiling. In W. Blum, P. L. Gal braith, H.-W. Henn & M. Niss (eds.) Modeiling and applications in mathematics education. The 14th /CMI Study (pp. 137-144). New York: Springer.
- Gravemeijer, K. (1999). How emergent models may foster the constitution of formal mathematics. Mathemati ca/ Thinking and Learning. (2), 155-177.
- Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as dif ferent sides of the same coin. Educational Studies in Mathematics, 22, 1-36.
- Steinbring, H. (2005). The construction of new mathematical knowledge in classroom interaction: An episte mological perspective (Vol. 38). Springer Science & Business Media.
- Thompson, P. W., & Carlson, M. P. (2017). Variation, covariation, and functions: Foundational ways of thinking mathematically. In J. Cai (Ed.), Compendium for research in mathematics education, 421-456. Reston, VA:National Council of Teachers of Mathematics.
- UVM (2006). Fremtidens matematik i folkeskolen. Rapport fra udvalget til forberedelse af en handlingsplan for matematik i folkeskolen. Undervisningsministeriet.
Eksempel: Matematikmorgener og morgenbrusebadet
Vækkeuret ringer!
Din hånd rammer uret, som falder på gulvet. Du får fat i det og slukker det med et suk.......
Du vender dig om på den anden side og prøver at forestille dig, at det er blevet lørdag. Men så mærker du den – lysten. Lysten til at komme i gang fordi der står Matematik morgener på skemaet. ”Muntre Matematik Morgener med Morten & Mikael”, tænker du.Klokken 8:00 skal du være sammen med alle de andre. En ny og spændende dag står forventningsfuld og venter på at blive taget i brug af netop dig!
Så tager du dine matematik-briller på, rejser dig fra din varme seng og går ud på badeværelset. Tjekker måske lige el-måleren undervejs?
På badeværelset smiler spejlet til dig, mens du søvndrukkent ser efter, om du er sluppet for bumser i løbet af natten.
Du børster tænder og forestiller dig måske, hvor sjovt det ville være at se, hvor lang en stribe du kunne lave, hvis du trykkede al tandpastaen ud......
Du lader det varme vand pjaske ned over din krop i flere minutter – hov, hvor meget vand gik der egentlig til det?
Opgave:
Lav nøjagtige optegnelser over det du ser med dine matematikbriller – fra du vågner til, du møder på skolen.
Dine notater skal så bearbejdes matematisk, og dine resultater og overvejelser skal formidles på et stykke A3-papir i et indbydende layout. Du har 4 moduler til det hele.