Epidemimatematik: Modeller
Epidemimatematik anvendes til at beskrive og overvåge, hvordan epidemier udvikler sig. Matematikken kan i et vist omfang forudsige epidemiers forløb og give grundlag for at stoppe eller bremse epidemier. Se eksempler på simple modeller og aktiviteter, fx modellen 'netværkssygdom' og spillet 'Counter Plague'.
En epidemi udvikler sig ved, at de smittede smitter andre. Hvis hver smittet smitter to andre, og det tager en uge, vokser det med 2, 4, 8, 16… nye smittede om ugen. Det må jo stoppe, eller gå delvis i stå, om ikke før, så når hele Jordens befolkning er smittet. Desuden bliver de smittede immune – i kortere eller længere tid – så der er færre og færre at smitte. Der går måske tid, inden den smittede smitter. Der går tid, inden den smittede viser sygdomstegn (inkubationstiden). Man smitter kun personer, man møder eller indirekte får kontakt med gennem for eksempel inficerede overflader, så en detaljeret model skal tage i betragtning, hvordan befolkningen mødes.
Undervisning i epidemimodeller
I det følgende er der forslag til aktiviteter, hvor eleverne arbejder med grundlæggende egenskaber ved epidemier i såkaldt diskrete epidemimodeller. Forslagene er inspireret af NRICH.
Find flere eksempler på aktiviteter på NRICH's websitet.
Eksempel: Netværkssygdom og Stå-op-sygdom
Del 1. Stå-op-sygdom
Opgave
- Første runde: Én elev rejser sig (er smittet) og peger på to andre.
- Anden runde: De to rejser sig og hver peger på to andre.
- Tredje runde: De fire udpegede peger på to hver.
- Osv.
Spørgsmål til eleverne
- Hvor lang tid (hvor mange runder) tog det, før hele klassen var smittet?
- Hvad ville der ske, hvis hver smittede 3?
- Hvad nu, hvis klassen var større?
Del 2. Et (socialt) netværk
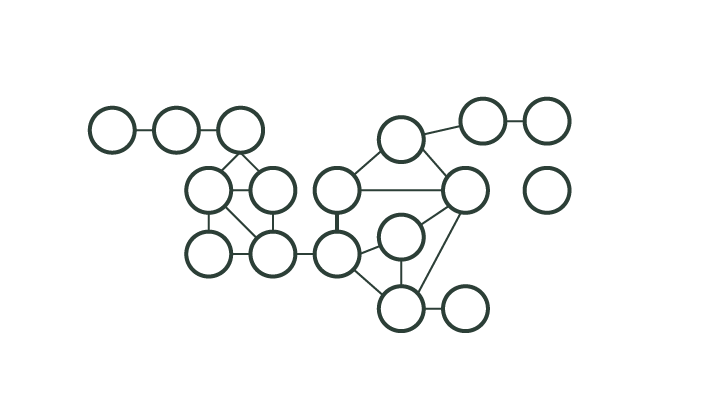
Opgave

- Vælg en knude (cirklerne) som den første smittede.
- For hver "naboknude" – dem, der er forbundet med den smittede - slår man med en terning.
- Hvis man slår 1 eller 2, smittes denne ikke. Ellers smittes den.
- Den, der var smittet først, markeres som immun og kan ikke smittes senere.
Eksempel på et forløb
- Knude nummer 5 smittes først.
- 5 smitter så knuderne 3 og 6. Og 5 er derefter immun. (Knude 9 smittes ikke – der slås med en terning for at se, om man smittes).
- 3 smitter 2 og 4, 6 smitter 8 og 9. De er derefter immune.
Spørgsmål til eleverne
- Hvordan udbredes sygdommen?
- Får alle den?
- Er det samme resultat hver gang?
- Hvad er betydningen af valg af den første knude?
- Hvad betyder reglen med terningkastet?
- Se på knude 7 i sidste figur. Den kan ikke smittes, fordi 6 er immun. Hvilke knuder skal være immune (vaccineres) for mest effektivt at forhindre sygdommen i at sprede sig?
Eksperimentér med andre netværk på Complexity explorables
Eksempel: Spil Counter Plague
Opgave
Man skal bruge en terning og 20-30 brikker pr. gruppe, der spiller. Hver gruppe vælger en farvet terning som i figuren og følger de regler, der er angivet. Tallene ud for terningerne siger, hvor mange nye smittede, der er, hver gang man slår.
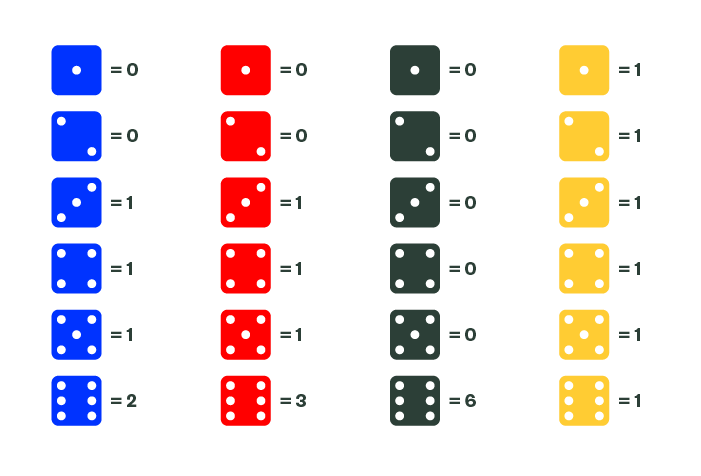
- Læg en brik på bordet – den første smittede - trin 0.
- Slå en gang med terningen
- Læg det antal brikker op, der passer til terningkastet. (Slår man 6 og har den blå terning, lægges 2 brikker. Slår man 6 og har den røde, lægges 3). De lægges til højre for den første brik. Det er Trin 1 i sygdommen.
- Slå nu en gang med terningen for hver smittet fra Trin 1, og læg de næste smittede til højre for den, der har smittet dem
- Gentag 4. Bliv ved, til epidemien dør ud, eller I løber tør for brikker.
Eksempel
Først med den blå terning:
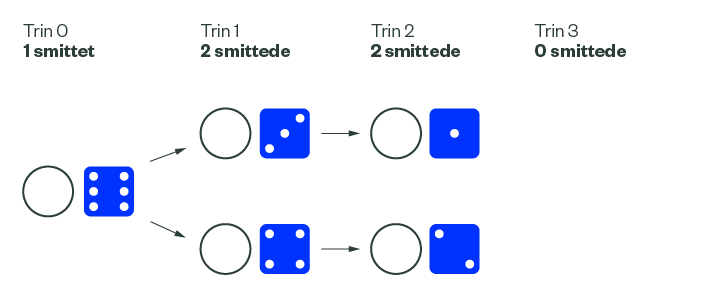
Derefter med den røde terning:
Prøv selv med andre terningregler – fx den grønne og den gule.
Spørgsmål til eleverne
- Hvor mange smitter en smittet i gennemsnit (det er kontakttallet)?
- Hvad skal det gennemsnit være, hvis epidemien skal dø ud?
- Hvordan kan man beskrive superspredere?
- I netværksmodellen?
- I Counter Plague?
Prøv flere online spil uden terninger på NCTM's websitet
til: Grundskole, Erhvervsskole og Gymnasie
emne: EPIDEMIMATEMATIK
UDGIVET: 2021