Epidemimatematik: Årsag og virkning
Epidemimatematik anvendes, når man vil bremse sygdomsudbrud. Når man vil kende årsagen til udbruddet, skal det afdækkes, hvad de syge har været udsat for, og hvad der så kan være årsagen til, at de er blevet syge. Dette kan give anledning til overvejelser og ræsonnementer om årsag og virkning. Se eksempler på matematikværktøjer til analyse af udbrud.
Sygdomsdetektiver
Epidemiologer kaldes sygdomsdetektiver, bl.a. af det amerikanske Centers for Disease Control and Prevention, som svarer til vores Sundhedsstyrelse. Den danske læge Peter Panum var blandt verdens første sygdomsdetektiver. Hans opdagelse af, at eksempelvis mæslinger smitter fra person til person og ikke rammer tilfældigt, gav mulighed for at stoppe et mæslingeudbrud på Færøerne i 1846 og et koleraudbrud på Lolland. Begge gange ved karantæne og begrænsning i rejseaktivitet – lockdown i moderne sprog. (Kilde 1)
Ved alvorlige sygdomme skal det gå stærkt. Det skal afdækkes, hvad symptomerne er, hvilken sygdom det kan være, og hvordan de syge mon har fået den?
Hvis det er en fødevarebåren sygdom, vil man gerne finde tilbage til forhandleren og stoppe salget af denne fødevare. Der har eksempelvis været en del udbrud af norovirus (såkaldt roskildesyge), som i sidste ende blev sporet til frosne hindbær og i andre tilfælde til østers. Bakterier som Salmonella og Campylobacter er andre hyppige årsager til fødevarebårne sygdomsudbrud.
Diagram over risiko
Et nyttigt værktøj er en afklaring af, hvad de syge har været eksponeret for – spist, drukket eller deltaget i. Lige så vigtigt er det at spørge de raske: Hvis 100 mennesker har spist ærter i kantinen, og 60 af dem er blevet syge, kunne det se mistænkeligt ud, men hvis nu 75 af dem, der ikke spiste ærter, er blevet syge, er ærterne måske ikke så meget i kikkerten. Måske har det ikke noget med ærterne at gøre. Man laver et diagram over risiko (attack rate).
Diagram for eksemplet med ærterne:
| Ja: syg | Ja: rask | I alt | Risiko | Nej: syg | Nej: rask | I alt | Risiko | |
|---|---|---|---|---|---|---|---|---|
| Spist ærter | 60 | 40 | 100 | $\frac{60}{100}$ 60% | 75 | 125 | 200 | $\frac{75}{200}$ 37,5% |
Man kan analysere den slags diagrammer med statistiske værktøjer. I første omgang kan man udregne den relative risiko, som her er
$\frac{60}{37,5}= 1,6$
Risikoen for at blive syg, hvis man har spist ærter, divideret med risikoen, hvis man ikke har spist ærter. (Kilde 2)
Eksempel: Analyse af relativ risiko
Maveonde til en fødselsdagsfest
Der har været udbrud af maveonde til en børnefødselsdag, og man kortlægger det, børnene har været eksponeret for. En hypotese om, at det stammer fra hjemmelavet is med rå æg, afvises, da isen ikke var med rå æg og to af de syge børn var taget hjem, før isen blev serveret. Morale: Man skal ikke drage forhastede konklusioner. Fødselsdagen blev holdt i den lokale svømmehal. Nu er hypotesen, at børnene blev syge der.
Analyse af den relative risiko:
Her er konklusionen, at de er blevet syge af at sluge vand fra børnebassinet. Bemærk, at der faktisk er 2, som ikke har slugt vand, men alligevel er blevet syge. Og 1, der har slugt vand, men ikke er blevet syg. Der er altså ikke altid en soleklar årsag-virkning-sammenhæng. Prøver af vandet kan underbygge konklusionen. (Kilde 6)
Korrelation vs. kausalitet
Hvis man konkluderer noget for tidligt, kan kuren være forkert. Det kan eksempelvis sagtens være, alle de syge har noget til fælles, som ikke har noget med sygdommen at gøre. Sammenfald af to ting er ikke det samme som, at der er en årsagssammenhæng. Som statistikerne siger: Korrelation er ikke det samme som kausalitet.
Eksempel: Analyse af sygdomsudbrud
Feber ved floden
Her er nogle oplysninger fra et udbrud af 'Rift Valley fever' i Kenya, før man vidste, hvilken sygdom det drejede sig om. Både dyr og mennesker var syge:
- 75% af de syge har håndteret rå mælk eller råt kød.
- 67% har haft kontakt til et sygt dyr.
- 25% har slagtet dyr.
- 10% har haft kontakt til en syg person.
Det er fristende at stoppe her og slå alle dyr ned, men der blev spurgt mere, og man fik så oplysningerne i tabellen:
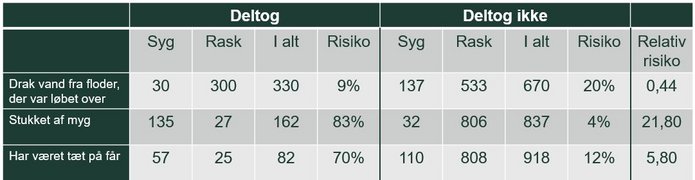
Det er tilsyneladende myggene, der er problemet, sammen med får, som bliver syge og giver smitten videre via myggene. Bekæmpelsen går i gang; man uddeler myggenet, insektspray osv. Man observerer, at udbruddet bremses, så det var den rigtige kur. (Kilde 3 og 7)
Epikurver
Andre matematikværktøjer til analyse af et udbrud kan være epikurver. Et plot af antal smittede pr. dag kan afsløre, om smitten er sket ét sted, om det smitter fra person til person, og om udbruddet er overstået.
Fire typer smitte, som kan beskrives i kurver:
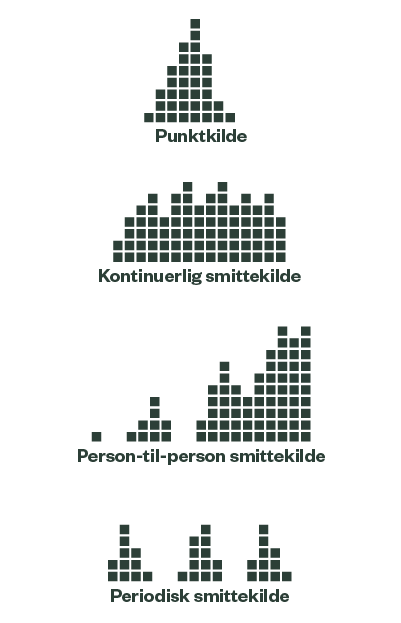
- Punktkilde
Årsagen er den samme for alle de smittede og har kort varighed, fx et fælles måltid, en fødevare med kort holdbarhed eller en begivenhed. - Kontinuerlig smittekilde
Samme årsag, men den er til stede over en længere periode. Eksempelvis en fødevare med lang holdbarhed. - Person-til-person-smitte
Et enkelt sygdomstilfælde vokser over tid til større og større patientgrupper. Typisk i samme familier eller arbejdsplads. Afstanden mellem toppene er inkubationstiden – tiden fra smitte til sygdommen bryder ud. - Periodisk smittekilde
Flere enkeltudbrud. Afstanden svarer ikke til inkubationstiden. (Kilde 4)
Kortlægning af smittetidspunkter
En kortlægning af smittetidspunkter og transportveje var central i Panums analyse af mæslingeudbruddet på Færøerne i 1848. (Kilde 5)
Som man kan se på illustrationen, er kortlægning her bogstaveligt talt at indtegne data på et landkort. Såvel smittetidspunkter som de veje ad sejlruter og veje over land, man havde i perioden.
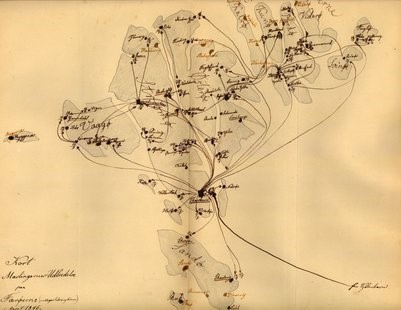
Kortet over spredningsvejene er fra Rigsarkivet, Sundhedsstyrelsen, Journalsager 1806-1981, pk. 120 (sag 11/1847).
Netværket af transportveje/rejser er et andet eksempel på et matematisk værktøj. Det kan repræsenteres med et abstrakt netværk, en graf. Knuderne er udbrudsstederne og forbindelserne, kanterne, er transportvejene. Bemærk, hvordan Torshavn er centralt for udbredelsen.
Diskussioner om årsag og virkning i klassen
Årsag og virkning kan diskuteres i klassen med udgangspunkt i elevernes egne observationer eller mere overordnede spørgsmål om sammenfald, der måske ikke er årsagssammenhænge:
- Det kan være de fjollede:
"Jeg har glemt mine handsker og nåede ikke bussen, og sådan var det også i tirsdags." Naturlige spørgsmål: "Har du altid glemt dine handsker, når du kommer for sent til bussen?" Og omvendt: "Kommer du altid for sent til bussen, når du har glemt dine handsker?" Hvis der ser ud til at være sammenfald – svarene er næsten altid nej på de to spørgsmål, så 'ser ud til' er i virkeligheden et statistikspørgsmål - kan man lede efter en underliggende forklaring (en såkaldt confounder). "Glemmer du handskerne og kommer for sent til bussen, fordi du er stået for sent op og skal skynde dig afsted?" - Eller de mere komplicerede:
Fx om rygning og lungekræft eller allergi og kæledyr i hjemmet. Spørg klassen, hvad man skal vide for at se, om der er en sammenhæng, og om det ene er årsag til det andet. Er der noget data, man kan bruge?
Er der en sammenhæng mellem overvægt og at drikke sukkerfri cola? Hvis der er en sammenhæng, drikker man så sukkerfri cola, fordi man er overvægtig eller bliver man overvægtig, af at drikke sukkerfri cola? Eller er der en underliggende forklaring på begge? - På højere niveauer:
Statistiske metoder til at belyse korrelation og kausalitet: Definition af korrelation. Eksempler på sære korrelationer. Metoder såsom randomiserede kontrollerede forsøg.
til: Grundskole, Erhvervsskole og Gymnasie
emne: EPIDEMIMATEMATIK
UDGIVET: 2021
Forfatter
Lisbeth Fajstrup
Lektor Emerita, ph.d.
Institut for Matematiske Fag, AAU
Leg sygdomsdetektiv
- Solve the Outbreak
Spil med eksempler på epikurver og udbrud. - Udbrudshåndbogen (s. 12)
Opklar et fødevarebåret udbrud ved hjælp af fødevarestyrelsens 10-punktsplan. - Videnskab.dk
Idéer til forløb om korrelation og kausalitet.
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
-
DR. Opslag: Mæslingeudbrud på Færøerne i 1846 kortlagde virussygdommens smittevej. Lokaliseret april 2021 på: https://www.dr.dk/nyheder/viden/naturvidenskab/maeslingeudbrud-paa-faeroeerne-i-1846-kortlagde-virussygdommens
-
Fødevarestyrelsen, Statens Serum Institut, DTU Fødevareinstituttet (2018, s. 40) Udbrudshåndbogen Lokaliseret april 2024 på: https://foedevarestyrelsen.dk/Media/638229298565475941/H%C3%A5ndbog%20i%20opklarings%20af%20f%C3%B8devare-%20eller%20vandb%C3%A5rne%20sygdomsudbrud%20januar%202018.pdf
-
Fødevarestyrelsen. Opslag: Rift Valley Fever. Lokaliseret september 2023 på: https://foedevarestyrelsen.dk/dyr/dyresundhed/dyresygdomme/rift-valley-fever
-
Fødevarestyrelsen, Statens Serum Institut, DTU Fødevareinstituttet (2018, s. 22) Udbrudshåndbogen Lokaliseret april 2024 på: https://foedevarestyrelsen.dk/Media/638229298565475941/H%C3%A5ndbog%20i%20opklarings%20af%20f%C3%B8devare-%20eller%20vandb%C3%A5rne%20sygdomsudbrud%20januar%202018.pdf
- Danmarkshistorien. Opslag: Uddrag af beretning. Lokaliseret august 2024 på: https://danmarkshistorien.dk/leksikon-og-kilder/vis/materiale/uddrag-af-laege-andreas-heinrich-manicus-beretning-fra-faeroeerne-i-forbindelse-med-maeslingeepidemien/
- CDC. Opslag: Birthday Party Gone Bad. Lokaliseret april 2021 på https://www.cdc.gov/mobile/applications/sto/508STO.html#outbreak2
- CDC. Opslag: Up Sick Creek. Lokaliseret april 2021 på https://www.cdc.gov/mobile/applications/sto/508STO.html#outbreak1