Eksempler
TALLENES TALE OG SIMPSONS PARADOX

Punktlighed er en vigtig parameter i konkurrencen mellem flyselskaber. Den angives som andelen af punktlige flyvninger i en periode, hvor denne er målt - altså,
$\frac{\text{antal punktlige flyvninger}}{\text{antal flyvninger i alt}}$
hvor ”punktlige flyvninger” fx kan defineres som flyvninger med ankomsttid senest i følge tidsplanen. Interessen for kunderne i de historiske tal ligger i, at de kan bruges som estimat for fremtiden – lidt som når man bruger historiske vejrdata til at lave vejrudsigter, men også meget simplere, fordi man simpelthen antager, at ”fremtiden bliver nogenlunde som fortiden”. Mere teknisk: vi bruger frekvensen af rettidige flyvninger, som er observeret, som et estimat for sandsynligheden for rettidighed i fremtiden.
Her er et (konstrueret) talmateriale, som flyselskabet Scanair bruger til at argumentere for, at de er mere punktlige end konkurrenten Air Baguette.
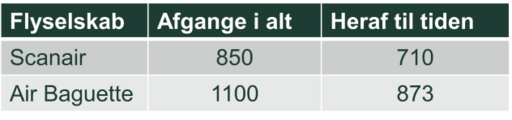
Tabellen viser afgange fra Københavns Lufthavn i løbet af 2022 på de to destinationer, som begge flyselskaber betjener, og hvor de altså konkurrerer. Andelene af rettidige flyvninger er for Scanair $\frac{710}{850}≈0.84$, mens den for Air Baguette er $\frac{873}{1100}≈0.79$. Så der er ingen tvivl vel? 84% af Scanairs flyvninger er rettidige, mod kun 79% af dem med Air Baguette.
Air Baguette hævder alligevel, at det er dem, som er mest punktlige. De præsenterer data for hver af de to destinationer, som begge flyver til og fra København, nemlig Paris og Stockholm.
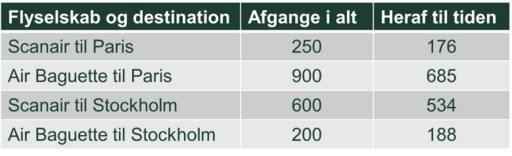
Og beregner vi andelen af rettidige flyvninger på de to destinationer, ser vi da også at den er højest for Air Baguette - i begge tilfælde (fx er $\frac{176}{250}<\frac{685}{900}$). Ikke desto mindre er det de samme flyvninger, som i den forrige tabel, nu blot delt op i fire grupper i stedet for to. Hvordan kan det nu gå til?
En mulig forklaring fås ved at se på rettidigheden af fly til Paris og Stockholm, for begge selskaber under et.
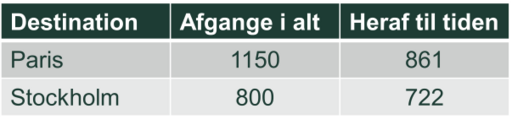
Vi ser straks, at andelen af punktlige flyvninger er størst, når vi ser på flyvninger til Stockholm. Det kunne måske skyldes forhold i de to lufthavne såsom trafiktæthed, strejker mm., og i første omgang kunne man måske tænke, at det er irrelevant for sammenligningen mellem Scanair og Air Baguette. Men det er det ikke. Tallene ovenfor viser nemlig, at Scanair mest flyver til Stockholm, mens Air Baguette hyppigere flyver til Paris.

Hvis der nu er vanskeligere forhold i Paris end i Stockholm, kunne forskellen mellem selskaberne, (når vi ser på alle deres flyvninger under et), simpelthen skyldes, at Air Baguette mest flyver til Paris. Air Baguettes sammenligning viser så, at dette selskab er bedst på begge destinationer – både Stockholm og den ”vanskeligere” lufthavn i Paris. Dertil kommer, at kunder typisk ved, hvor de skal hen, og dermed er mere interesserede i selskabernes punktlighed på deres destination end på, hvordan de klarer sig totalt.
Ovenstående eksempel illustrerer det såkaldte ”Simpson paradoks”, som i almindelighed handler om, at et datamateriale kan vise modsatte tendenser alt efter, hvordan det inddeles i grupper – her efter lufthavn og flyselskab. Det kan bruges som eksempel på, at selvom talmateriale kan se ret objektivt og entydigt ud, så kan et spørgsmål sommetider besvares på flere måder afhængigt af, hvordan materialet bruges og fortolkes.
Opgaver
- Det ser ovenfor ud som om, vi i sidste ende giver Air Baguette ret. Prøv at finde muligheder for at forsvare Scanair. (Vink: kunne punktligheden på en destination skyldes flyselskaberne?)
- Simpson’s paradoks kan give anledning til fejlslutninger, som har alvorlige konsekvenser. Lav en tilsvarende opgave (med de samme eller andre tal som i eksemplet med punktlighed), som handler om effektiviteten af to præparater Machopill og Femimed, hvor det første mest bruges af mænd og det andet mest af kvinder – og hvor man, afhængigt af om det tages i betragtning, får forskellige vurderinger af de to præparater.
KORRELATION ER IKKE KAUSALITET
Eksemplet ovenfor illustrerer et par andre begreber. Når der ikke er samme andel af punktlighed hos to flyselskaber, kan vi komme til at sige, at punktligheden afhænger af flyselskabet. Når vi udtrykker det sådan, lyder det som om, det er flyselskabet, som er årsagen. Eksemplet viste også, at det i hvert fald ikke er sikkert, at der er en årsagssammenhæng (også kaldet kausalitet). Mere korrekt er det at sige, at punktlighed og flyselskab er indbyrdes afhængige – eller, på fagsprog, er korrelerede således, at fx en høj punktlighed ”følges ad” med valg af bestemte flyselskaber (der er en korrelation). Det er ikke sikkert, at der er nogen årsagssammenhæng overhovedet – korrelationen kunne således opstå pga. andre forhold, fx de destinationer, som selskaberne flyver (mest) til. At forveksle korrelation med årsagssammenhæng (kausalitet) hører til de værste og mest almindelige fejltyper, når det gælder fortolkning af statistiske data.
Der findes flere metoder til at undersøge, om to størrelser i et datasæt er korrelerede. Lad os fx se på pris og alder for 6 brugte biler hos en bestemt forhandler.
Man kan starte med at plotte tallene fx vha. Excel:
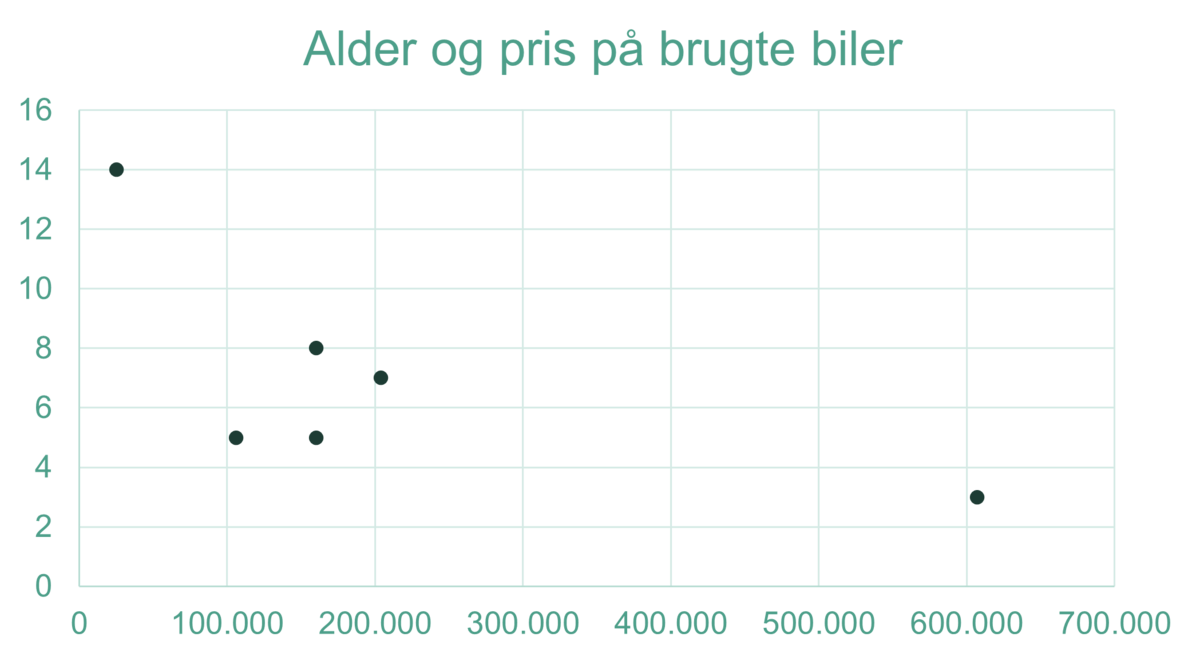
Kvalitativt ser det måske ud til, at dyre biler er yngre, men det er ikke entydigt. Hvis vi ser bort fra den dyreste og den billigste bil (”outliers”, som også er hhv. den yngste og den ældste), så er billedet ikke klart. Excel kan vise os en tendenslinje for det samlede datasæt eller for det, hvor de to outliers er fjernet – de ser meget forskellige ud. Excel kan også beregne det såkaldte R-kvadrat, som er et statistisk mål for korrelationen (se fx https://en.wikipedia.org/wiki/Pearson_correlation_coefficient for yderligere detaljer) og specielt, om der er en lineær sammenhæng mellem de to datasæt (der findes tilsvarende mål for andre sammenhænge). Men sådan et mål kan ikke stå alene: vi må vide mere om situationen, for at udtale os om evt. årsagssammenhænge. Hvis brugtbilhandleren udelukkende forhandler en bestemt bilmodel – hvilket nok er sjældent – så kunne der måske være større grund til at fæste lid til, at prisen på bilen til en vis grad, skyldes alderen. Man kunne fremhæve andre forbehold ift. ovenstående data: fx oplysninger om 6 biler er nok for lidt til at analysere sammenhængen mellem pris og alder, selvom det heller ikke er sådan, at et stort datamateriale altid giver bedre information.
Problemstillingen omkring korrelation og kausalitet er yderligere belyst i temaet Epidemimatematik.
UAFHÆNGIGHED
Et udsagn om, at en bestemt sygdom rammer mænd og kvinder lige meget, svarer til, at vi vil forvente, at andelen af kvinder, som har sygdommen, er den samme som andelen af mænd, der har den. Vi kan illustrere dette med en simpel figur:
Hvis antallet af kvinder og mænd i en stikprøve betegnes som hhv. $k$ og $m$, antallet af syge kaldes $s$, og antallet af syge kvinder (hhv. mænd) betegnes $s_k$ (hhv $s_m$), betyder uafhængighed af sygdom og køn altså
$\frac{s}{k+m} = \frac{s_k}{k} = \frac{s_m}{m} \quad \quad \quad \quad (*)$
Pga. ”tilfældige afvigelser” i en stikprøve vil det sjældent gælde eksakt, og man har da også metoder til at bedømme, hvor store afvigelser der kan være fra (*), uden at det anfægter hypotesen om uafhængighed (”tests” for uafhængighed”); sådanne tests er ret indviklede matematisk set, men kan let udføres med et værktøj (se fx https://www.statology.org/chi-square-test-of-independence-calculator/).
I en sandsynlighedsteoretisk model er (*) en antagelse, som altså (i modellen) gælder eksakt. Af (*) følger:
$\frac{k}{k+m} = \frac{s_k}{s} \ \text{og} \ \frac{m}{k+m} = \frac{s_m}{s} $
hvoraf
$\frac{k}{k+m} \cdot \frac{s}{k+m} = \frac{s_k}{k+m} \ \text{og} \ \frac{m}{k+m} \cdot \frac{s}{k+m} = \frac{s_m}{k+m}$
svarende til at andelen af syge kvinder (hhv. syge mænd) fås som produktet af andelen af kvinder (hhv. mænd) og andelen af syge. I sandsynlighedsteoretisk notation:
$P(K)P(S) = P(K \cap S) \quad \text{og} \quad P(M)P(S) = P(M \cap S)$
Generelt: to hændelser $A$ og $B$ kaldes uafhængige, hvis $P(A \cap B) = P(A)P(B)$.
Denne definition er ganske abstrakt og ikke særlig meningsgivende; hvorimod den følgende alternative form, (hvor vi bruger definitionen af symmetrisk sandsynlighed), er meget mere sigende:
$P(A) = \frac{P(A \cap B)}{P(B)} = \frac{\text{antal elementer i A som også er indeholdt i B}}{\text{antal elementer i B}}$
Højresiden angiver andelen af elementer i $B$, som også er indeholdt i $A$, og det samlede udsagn siger så, at andelen af $A$-elementer i det samlede udfaldsrum, er det samme som andelen af $A$-elementer i $B$. Den sidste andel kaldes i øvrigt for den betingede sandsynlighed af $A$ givet $B$, og betegnes $P(A|B)$.
Uafhængighed af $A$ og $B$ betyder altså at $P(A) = P(A|B)$
Opgave:
Vis, at uafhængighed af $A$ og $B$ også betyder at $P(B) = P(B|A)$. Hvad må vi forudsætte om $A$ og $B$ for, at de brøker, som indgår, giver mening? Hvad hvis denne betingelse ikke er opfyldt?
Eksempel:
Når vi slår to gange med en terning, antager vi, at udfaldene af de to slag er uafhængige. Hvis fx $A$ er hændelsen, at vi får en sekser i første kast, og $B$ er hændelsen, at vi får mindst to i andet kast, er sandsynligheden for, at de begge indtræffer:
$P(A \cap B) = P(A)P(B) = \frac{1}{6} \cdot \frac{5}{6} = \frac{5}{36}$
Det fremgår også, hvis vi skriver alle udfald af de to kast (kombineret) op, idet netop 5 af disse vil have 6 som resultat af første kast, og mindst 2 som resultat af det andet.
Mere generelt: hvis vi betragter $n$ hændelser $A_1,...,A_n$, kaldes disse uafhængige hvis1
$P(A_1 \cap ... \cap A_n) = P(A_1) \cdots P(A_n)$
Det såkaldte ”multiplikationsprincip” siger, at man kan få sandsynligheden for en kombination af uafhængige hændelser ved at tage produktet af hændelsernes sandsynligheder. Men det er altså bare en måde at sige på, at hændelserne er uafhængige – så det skal man godtgøre på anden vis!
Opgave:
Hvad er sandsynligheden for at få mindst to seksere i fire uafhængige terningkast?
Eksempel:
Hvis vi ser på to elever, er sandsynligheden for, at de har forskellige fødselsdage: $\frac{364}{365}$ , når vi ser bort fra muligheden af at have fødselsdag 29/2. Kommer en tredje elev til, er sandsynligheden for, at denne elev har en anden fødselsdag end de to første: $\frac{363}{365}$. Sandsynligheden for, at alle tre har forskellige fødselsdage, er, (idet vi antager at den tredies fødselsdag er uafhængig af de to førstes): $\frac{364}{365} \cdot \frac{363}{365}$. Fortsætter vi på samme måde til vi har $n$ elever, får vi, at sandsynligheden for, at de alle har forskellige fødselsdage er:
$\frac{364 \cdot 363 \cdot ... \cdot (365-n+1)}{365^{n-1}}$
hvor produktet i tælleren har $n-1$ led. Denne sandsynlighed er altså en funktion af $n$ , som er afbildet nedenfor for $n=1,2,...,28$.
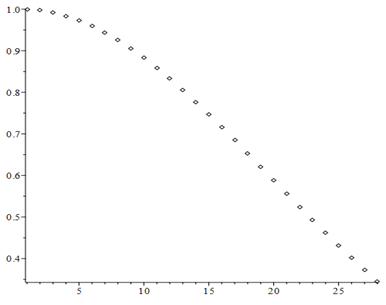
Ved aflæsning (eller direkte beregning) ser vi at sandsynligheden første gang bliver mindre end 0.5, når $n=23$. I en klasse med mindst 23 elever er det altså overvejende sandsynligt, at mindst to elever har samme fødselsdag!
Opgave:
Hvor mange elever kan en lærer have, uden at det bliver overvejende sandsynligt at en af eleverne har samme fødselsdag som læreren? (Se igen bort fra skuddagen . Svaret er: 253. Hvor bruges uafhængighed i din besvarelse)?
Stokastiske undersøgelser: Eksempler
I nedenstående forslag til undersøgelser eksemplificeres principperne for stokastisk undersøgelse på forskelligt detaljeniveau, idet der til nogle gives links til mere udførlige beskrivelser af undervisningsplaner og observationer fra brug.
Undersøgelse 1 (daginstitution)

Emne: indsamling og repræsentation af data.
Spørgsmål: hvilke farver sko bruger børnene her på stuen (institutionen)?
Materialer:
- kartonark i forskellige farver, fx hvid, brun, sort, rød osv.
- tavle/whiteboard og tilsvarende skriveredskaber, herunder tykke tudser.
- papirark med skriveunderlag og blyant til grupper af børn.
Forløb:
Start med at spørge: hvilken farve sko havde I på i morges? Efterhånden som børnene nævner nye farver sættes et tilsvarende ark op på en magnetisk tavle eller whiteboard, som alle børnene kan se, og skriv farvens navn på arket (det sorte ark kan være forsynet med hvidt felt at skrive ”sort” på).
Nu formuleres spørgsmålet, evt. gradvist: ”Hvad tror I er de mest almindelige farver? – for voksne, for børn? Her på stuen? På hele institutionen”?
Når det endelige spørgsmål er formuleret, skrives det på tavlen, og man kan spørge:
- Hvad tror I er den mest almindelige farve? Næstmest? Etc. Man ordner nu arkene i rækkefølge efter hvad børnene siger, evt. ved håndsoprækning.
Det er fase 1 som grundlæggende består i at etablere børnegruppens formodninger om hvad svaret er.
Fase 2: Hvordan kunne vi undersøge om vi har ret? – Tælle alle sko i garderoben, etc. Hvordan kunne vi tælle? Skal vi tælle flere steder? Kan vi fordele arbejdet – hvordan (fx hver gruppe tæller en bestemt farve sko, et bestemt sted, etc.)? Skal vi skrive svarene ned?
Fase 3: børnene tæller sko et eller flere steder på institutionen, gerne i mindre grupper, hvor en skriver ned, en tæller, osv.; de fysiske forhold må selvfølgelig afgøre hvordan det kan organiseres. Datamaterialet samles herefter i plenum, ved at børnene nævner de antal de har fundet, som noteres på tavle/whiteboard under den pågældende farve. Opdages nye farver, laves ekstra ark til dem, og tallene noteres derunder.
Fase 4: var vores formodning rigtig? Skal vi ændre i kortenes ordning? Hvad kan evt. afvigelser skyldes? Har vi brug for mere data? Hvad betyder det at en farve er ”almindelig” eller ”sjælden”? Kan vi angive hyppigheden af en farve på andre måder end antal, så det ikke afhænger af hvor mange sko vi har talt i alt? Hvis vi fx har talt 20 par sko, og fundet 3 sorte par, er det det samme som hvis vi havde talt 50 par sko og fundet 6 sorte par? Etc.
Fase 5: formulere og evaluere konklusioner, fx ”hvide sko er mest almindelige her”, ”sorte sko er dobbelt så almindelige som røde”, etc. Stille nye spørgsmål: kunne svaret afhænge af om det er vinter eller sommer? Mon det er det samme i andre børnehaver? etc.
Undersøgelse 2 (indskolingen)

Emne: deskriptiv statistik.
Spørgsmål: hvor trafikeret er vejen ved skolen?
Materialer:
- Tavle/whiteboard
- Papirark med skriveunderlag
- Blyant til grupper af børn.
Forløb:
Fase 1: formulering af spørgsmål og diskussion af relaterede spørgsmål. Hvad betyder trafikeret? Vil vi fx undersøge, hvor mange biler der kører på vejen? Hvad med cykler og knallerter? Hvornår? Betyder det noget for os? Synes vi, vejen har meget trafik? Hvad gør man, hvis der er for meget trafik?
Fase 2: Hvad skal vi bruge for at svare på spørgsmålet? Billeder af vejen om morgenen? Hvor mange?
Hvis vi fx vil undersøge biltrafikken på vejen, hvad skal vi så gøre? Tælle biler i en bestemt periode? Hvor længe er det nødvendigt eller muligt at tælle? Skal man tælle dem, der kører i én retning, eller i begge retninger? Mon der findes data om vejens trafik på nettet? Kunne forskellige grupper af elever fx tælle forskellige slags trafik? Hvordan kunne vi ud fra data sige noget om, hvor trafikeret vejen er? Læreren inddeler eleverne i grupper og noterer disse på tavlen, som inddeles i parallelle kolonner med gruppenavn og medlemmer noteret foroven. Læreren peger på de tomme felter nedenunder: ”Her vil vi samle jeres svar, når I er færdige”.
Fase 3: Børnene arbejder nu i grupper med at indsamle data om trafikken på vejen, gerne med forskellige metoder. Grupperne forbereder derefter svar på spørgsmålet ud fra egne data. Evt. dataindsamling ved vejen skal naturligvis foregå med passende sikkerhedsforanstaltninger.
Fase 4: De indsamlede data deles nu i plenum ved, at læreren eller eleverne noterer konklusioner og data på tavlen i de parallelle felter.
Fase 5: Efterhånden som gruppernes svar gennemgås, engagerer læreren alle elever i validering: er svaret overbevisende? Er data gode nok? Kunne vi sige mere ud fra dem? – og efter at alle er gennemgået: hvordan kan vi måle, om en vej er trafikeret? Hvad er relevante data? Får man altid dobbelt så mange biler, når man tæller dobbelt så længe? Hvad betyder ”antal biler per minut”? Skal man tælle biler i mere end et minut for at svare på det? Hvordan finder man fx et bud på dette mål, hvis man har talt i 10 minutter? Afhænger det af tidspunkt på dagen? Er der forskel på antallet af trafikanter i de to forskellige retninger? Er forskellen tilfældig? etc.
Undersøgelse 3 (mellemtrin)

Emne: deskriptiv statistik.
Spørgsmål: hvor præcist kører bussen (toget)?
Forløb:
Her kunne fx arbejdes med en busrute, som mange af eleverne kender og evt. benytter. Der kan bedst arbejdes med data, som er ”lavet på forhånd”, fx en tabel, som viser faktiske ankomsttider ved et bestemt stop og det tilsvarende tidspunkt i køreplanen, fx over en hel dag eller et længere tidsrum; eller en tabel, som viser faktiske afgangstider for en bestemt afhang over en måned. Det kan være faktiske målinger eller konstruerede data (bare det oplyses). I analysen af data diskuteres så, hvordan man bedst måler ”præcision”: gennemsnit af forsinkelser? eller af forsinkelser over fx 5 minutter? Antallet af forsinkelser over 5 minutter, evt. relativt til det totale observationer? Hvad er egentlig en ”forsinkelse”, der betyder noget? Hvad kan man se på et histogram af data? Er der nogle tidspunkter, hvor præcisionen er bedre end andre? etc. (se også kilde 1)
Undersøgelse 4 (mellemtrin)

Emne: frekvens og symmetrisk sandsynlighed.
Spørgsmål: hvor mange røde kugler er der i flasken?
Materialer:
- tavle, papir og blyanter
- 10-15 små papflasker med plastiklåg
- et gennemsigtigt stykke plast
- røde og blå kugler
Forløb:
I flaskernes plastiklåg laves et cirkulært hul, og på indersiden af hullet fastlimes et gennemsigtigt stykke plast, som dækker hullet. Man skal nu anbringe fem kugler i hver flaske); disse skal alle være røde eller blå, men der er initialt samme antal (fx 2 røde og 3 blå, eller 5 røde) i de alle flasker. Hver flaske skal være lavet, så man kun kan se farven på én kugle gennem hullet, når flasken vendes på hovedet, (og så man ikke kan se noget i andre positioner).
Læreren viser de 10 flasker til kassen og fortæller, at de indeholder fem blå eller røde kugler, og at man kun kan se en kugle ad gangen. Spørgsmålet formuleres sammen med reglen om, at man ikke må skrue låget af for at kigge, men kun se gennem hullet. Læreren viser, hvordan flasken bruges (vende og se), fx på en ”lærerflaske”, som indeholder 5 blå kugler. Læreren igangsætter en diskussion af, hvordan man på denne måde kan finde ud af, hvor mange røde kugler der er i flasken. Forskellige hypoteser: ”vi skal kigge fem gange”. ”Men måske kommer den samme kugle frem hele tiden!” etc. Da det er oplyst, at der er 5 kugler i alt, fastslås, at antallet af røde kugler også vil fortælle, hvor mange blå der er.
Eleverne inddeles nu i grupper, som får hver sin flaske, og de går i gang med at undersøge dem som foreskrevet. Hav gerne et par ekstra flasker klar, hvis noget går galt i en gruppe.
Efter at eleverne har øvet sig lidt, deler læreren papir og blyant ud til grupperne og opfordrer dem til at skrive ned, hvad de ser i deres forsøg på at bestemme antal røde kugler i flasken. De skal efterfølgende vise deres resultat til resten af klassen og forklare, hvordan de kom frem til det.
Efter endnu en arbejdsperiode deles resultaterne.
I den fælles deling kommer nu forskellige datasæt på tavlen. Nogle har måske prøvet 5 gange flere gange, og fået forskellige antal røde, fx 3,2,1,4,4. De tror, der er 4 røde, fordi det optrådte flest gange.
Andre har måske prøve 20 gange, og set en rød kugle 7 gange og slutter, at 2 kuglerne er røde: det er lidt færre end halvdelen, men dog flere end 1 ud af 5. Og så videre.
Læreren griber ideen med brøker: andelen af røde kugler ud af de totale antal observationer kan beregnes som ”antal røde/totalt antal”. Denne beregning gennemføres nu på det samlede datasæt, fra alle grupper (i plenum). Ingen eller få af disse beregninger giver et pænt tal. Hvad skulle det være, hvis der er én rød kugle? Svar: $\frac{1}{5}=0.2$. Tilsvarende for 2, 3, og 4 kugler (da alle har set både røde og blå kugler, er 0 og 5 udelukket). Måske lægger man mærke til, at tallene ”nærmer sig” 0.4 des flere observationer, der er foretaget. Ellers opfordrer læreren til nye forsøg, som viser dette tydeligere, eller man kan prøve at beregne brøken ud fra alle gruppernes observationer under ét. Uanset metode, begynder tallet $0.4=\frac{2}{5}$ og dermed ”2 røde” at blive en alment accepteret formodning. Nu tillades eleverne at åbne deres flaske som ”validering”. Der kan evt. laves nye forsøg med andre (for eleverne ukendte) blandinger af 5 blå og røde kugler. Spørgsmålet er nu at verificere metoden: når vi laver et stort antal observationer, så vil brøken (frekvensen) efterhånden vise klart, hvor mange røde kugler flasken indeholder. Man kan så stille spørgsmålet: hvor mange observationer skal der til for, at man kan være sikker på flaskens indhold? Det kan på dette niveau kun undersøges empirisk, og hovedpointen er da også, at frekvensen af røde kugler ”nærmer sig” den sande frekvens (fx 0.4) des flere observationer, man laver – dog ikke skridt for skridt, men kun ”over mange observationer”. Eleverne kan tegne grafer for, hvordan frekvensen udvikler sig skridt for skridt for at indse dette.
Note til læreren: hvis der er $x$ af de fem kugler, som er røde, er den sande frekvens jo $\frac{x}{5}$. Dette er sandsynligheden for at se en rød kugle, når man vender flasken. Hvis man vender flasken $n$ gange, er sandsynligheden for at se en rød kugle $k$ gange, (hvor selvfølgelig $k$ er et af tallene $0,1,\dots,n$):
$\frac{n!}{(n-k)!k!} \left( \frac{x}{5} \right)^k \left(1 - \frac{x}{5} \right)^{n-k}$
svarende til at antallet af røde kugler, som ses, er binomialfordelt med antalsparameter $n$ og sandsynlighedsparameter $\frac{x}{5}$. Denne fordeling er pensum i gymnasiet, men ikke i grundskolen. Formlen ovenfor betyder fx, at hvis der er 2 røde kugler, og man vender flasken 10 gange, så er sandsynligheden for at se en rød kugle 4 gange lig med
$\frac{10!}{6! \cdot 4!} \left( \frac{2}{5} \right)^4 \left( \frac{3}{5} \right)^{6} \approx 0.25$
Det er altså langt fra sikkert, at man får den ”sande” frekvens $0.4 = \frac{4}{10}$ med bare 10 forsøg. Men man kan vise, at den observerede frekvens alligevel er tæt på 0.4 (fordelingens middelværdi), når antallet af observationer er stort nok. Matematikken bag dette ræsonnement går langt ud over gymnasiets matematik. Men man kan altså alligevel arbejde med fænomenet – ”empirisk frekvens nærmer sig teoretisk sandsynlighed, når der gøres virkelig mange observationer” – i skolen.
Der kan også arbejdes med simulering af eksperimentet fx ved hjælp af Excel. På mellemtrinnet kan eleverne arbejde med et program, som læreren har udviklet. I udskolingen kan eleverne med støtte til brug af relevante kommandoer i Excel selv udvikle et program til simulering af sådanne eksperimenter.
Se også kilde 2
Undersøgelse 5 (mellemtrin/udskoling)
Emne: symmetriske sandsynlighedsfelter, uafhængighed.
Spørgsmål: har eleverne i en klasse normalt forskellige fødselsdage?
Forløb:
Den sandsynlighedsteoretiske model er gennemgået i eksempel under Uafhængighed, og kan med passende forberedelse udvikles af eleverne selv, men det er en god idé, at spørgsmålet først undersøges uformelt, (hvad tror vi?) og ved dataindsamling (i egen og evt. andre klasser). Eleverne vil normalt tænke, at da der er 365 (evt. 366) forskellige mulige fødselsdage, så er det sjældent, at der lige er én fødselsdag, som deles af flere elever. Det kan også sagtens være, det ikke er tilfældet i én klasse…
Undersøgelse 6 (udskoling/gymnasium/EUD)
Emne: deskriptiv statistik, sammenligning af datasæt.
Spørgsmål: Hvilken virksomhed ville du helst arbejde i?
Forløb:
Eleverne får udleveret tre lister (fx regneark), som hver viser alle månedslønningerne i en mindre virksomhed (fx 20-30 lønninger pr. liste – eksempler findes i referencen ovenfor). Eleverne arbejder nu med at repræsentere data fx vha. punktplots og grupperede histogrammer og med at beregne og sammenligne deskriptorer som middelværdi, median, typetal, spredning osv.; evt. kan der også arbejdes med mere avancerede værktøjer som Gini-koefficient (ulighed), t-test for middelværdi, etc.
Se også kilde 3
Undersøgelse 7 (EUD/gymnasium)

Emne: frekvens, spredning, konfidensintervaller.
Spørgsmål: hvordan kan man bedømme, hvor stor en andel af varer, som er defekte, ved at undersøge en mindre stikprøve?
Forløb:
Man kan fx bruge arbejdsspørgsmål som:
- Vi har fået en vareprøve med 200 emner (fx 200 eksemplarer af en bestemt komponent til en maskine, eller portioner af en færdigret). Emnerne er udtaget tilfældigt af den samlede produktion. En nærmere undersøgelse viser, at 7 af emnerne i vareprøven er defekte. Hvad er fejlprocenten (=andelen af defekte varer)? Hvis der er produceret 1 million emner, hvor mange af disse er så ca. defekte?
- En ny prøve på 200 emner viser sig kun at indeholde 3 defekte emner. Hvordan ændrer det vores billede af fejlprocenten (svarende til andelen af alle emner som er defekte)?
Da det typisk ikke er praktisk umuligt at undersøge samtlige emner, der er produceret, ønsker vi at vurdere, hvor sikre vi kan være på resultatet af at undersøge en given vareprøve. Når vi har undersøgt en prøve af emner, kan man bruge https://www.statology.org/confidence-interval-proportion-calculator/ til at beregne et interval, hvor den ”sande” fejlprocent ligger med 95% sikkerhed (forstået sådan, hvis vi undersøgte 100 tilsvarende prøver, så ville ca. 95 af disse have en fejlprocent som ligger i intervallet; på det angivne link betegner $p$ det, vi ovenfor har kaldt fejlprocenten, mens $n$ er antallet af emner i vareprøven).
- Brug beregneren til at finde ud af, hvor stor en vareprøve, vi skal undersøge, hvis intervallet kun må have længde 1% (svarende til, at vi kan estimere fejlprocenten nogenlunde korrekt som et helt tal). Bemærk, at det afhænger af, hvad $p$ er – det ved vi selvfølgelig ikke, men her kan du bruge det første estimat baseret på a) og b).
- Hvordan vil du planlægge en undersøgelse af emner baseret på stikprøver, hvis du kan undersøge 100 emner om dagen, og resultatet skal foreligge indenfor fem dage?
- Hvad er matematikken bag beregneren? Tryk fx på det første link i linket ovenfor.
Undersøgelse 8 (EUD)
Emne: statistisk proceskontrol (kilde 4)
Spørgsmål: Hvordan læses og bruges et control chart?
Forløb:
Deltagerne får udleveret nedenstående (autentiske) repræsentation af produktionsdata, et såkaldt ”control chart”, som viser produktionen af tape i meter per uge. Man kan også udlevere data i et regneark, og derpå lade de studerende starte med at producere diagrammet (”control chart”) idet, de nævnte grænseværdier indtegnes som vandrette linjer.
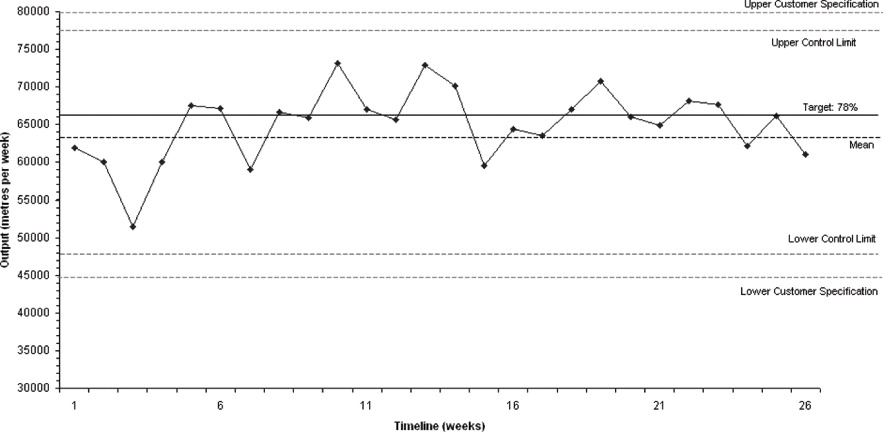
De nævnte grænseværdier betegnes i figuren med engelske fagtermer fra statistisk proceskontrol:
- Target er produktionsmål fastsat af virksomheden (her 66.500 meter per uge)
- Mean er middelværdien af produktionen i perioden, som vi ser på
- Upper/lower control limits er middelværdien plus/minus 3 standardvariationer af datasættet
- Upper/lower customer specifications er øvre og nedre grænser for produktionen, som her er sat af kundekrav
Man kan fx arbejde med tendenslinjer i mindre intervaller af datasættet: er der en stigende eller faldende tendens i visse perioder? Hvad kunne det betyde for produktionsstyring og indtjening? Det er også interessant at diskutere ”outliers”, dvs. usædvanlige datapunkter: hvad kunne de afspejle? Skal de evt. ignoreres? Endelig kan det være interessant at sammenligne forskellige control charts, fx ovenstående og nedenstående, som kommer fra samme virksomhed (de første 26 datapunkter i det sidste diagram er de samme, som dem i det første, men det kan deltagerne jo selv lægge mærke til). Kan vi tale om stabile og ustabile perioder? Hvordan kunne det defineres?
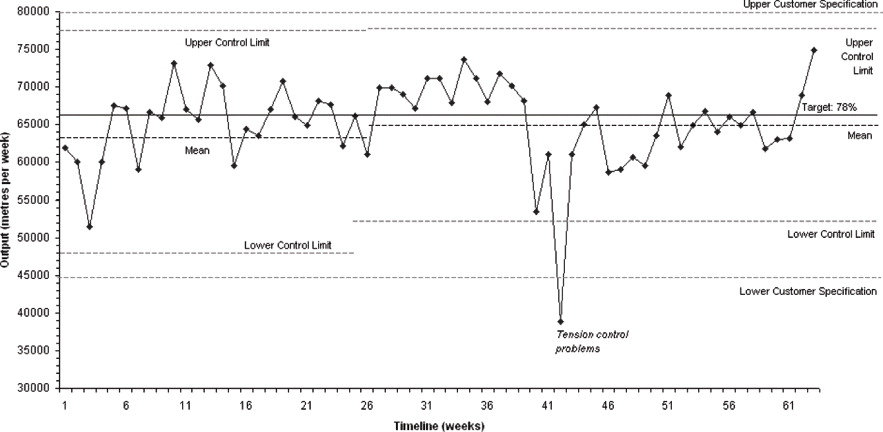
Undersøgelse 9 (gymnasialt niveau, men man kan arbejde med dele af det i udskolingen)
Emne: binomialfordeling, normalfordeling, grænseværdi af fordeling.
Spørgsmål: hvor mange gange får vi plat, når vi kaster $n$ gange med en mønt?
Forløb:
Det naive svar er, at det ved vi ikke, uanset hvad $n$ er. Men vi kan estimere andelen af kastene, som giver plat $k$ gange, som
$bin(n,k,0.5) = \frac{n!}{(n-k)!k!} 0.5^n$
hvor $bin$ i almindelighed kan beregnes vha. et matematikværktøj (evt. ved at bruge en normalfordelingsapproximation, hvis $n$ er stor). Undersøg nu, hvordan ”grafen” for denne funktion ser ud, når $n$ er stor. Hvorfor er det nyttigt at vide? Forbindelse til undersøgelse 7?
Undersøgelse 10 (gymnasialt niveau, men man kan arbejde med dele af det i udskolingen)

Emne: symmetrisk sandsynlighed, sandsynlighedsfordelinger.
Spørgsmål: Hvis vi kaster $n$ terninger et stort antal gange og hver gang noterer det samlede antal øjne, hvad er så de forventede frekvenser af de mulige øjental $(n,n+1,\dots,6n)$?
Forløb:
Hvis man slår med en 2 terninger, hvad er så sandsynligheden for hver af de 11 mulige øjensummer? Hvis vi slår med 2 terninger mange gange og hver gang noterer øjensummen, kan vi præsentere resultaterne i et histogram. Hvordan kommer det til at se ud?
Hvis vi slår med flere end to terninger på én gang, bliver det mere indviklet. Se fx:
https://www.tutorialspoint.com/dice-rolling-simulator-using-python-random (programmeringstilgang)
https://www.w3schools.com/statistics/statistics_normal_distribution.php (animerede løsninger uden forklaring)
https://www.lucamoroni.it/the-dice-roll-sum-problem/ (sandsynlighedsteoretisk modellering)
til: GRUNDSKOLE & GYMNASIE
emne: STOKASTIK
UDGIVET: 2023
Forfatter
Carl Winsløw
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Noter
1 Definitionen givet her er ikke strengt korrekt, da "produktformlen" faktisk skal gælde for alle udvalg af mængderne.
Kilder
-
C. Hellsten Østergaard (to appear). An Inquiry Perspective on Statistics in Lower Secondary School in Denmark and Japan–An Elaboration and Modelling of the Anthropological Theory of the Didactic Through Two Statistics Classrooms. European Journal of Science and Mathematics Education 10(4). Et andet eksempel på en undersøgende aktivitet for 6. klasse findes her.
- G. Brousseau, N. Brousseau, V. Warfield (2002): An experiment on the teaching of statistics and probability. Journal of Mathematical Behavior 20, pp. 363-441
- Cafuta, K. (ed., 2019). MERIA Modules, s. 43-58. https://meria-project.math.hr/sites/default/files/2019-10/MERIA%20Scenarios%20and%20Modules%20DEN.pdf
- Hoyles, C., Bakker, A., Kent, P. and Noss, R. (2007). Attributing meaning to representations of data: the case of statistical process control. Mathematical thinking and learning 9(4), 331-360.