Intro: Mellem umuligt og sikkert

MELLEM UMULIGT OG SIKKERT

Matematiske svar kræver ret præcise spørgsmål. Et dagligdags spørgsmål som ”Hvordan bliver vejret i dag?”, er ikke særlig præcist. Mere præcise spørgsmål kan bedre besvares matematisk, fx: hvor meget vil solen skinne i løbet af dagen, hvordan bliver temperaturen, og hvor meget nedbør kommer der. Fælles for disse spørgsmål er dog, at ingen kan besvare dem med fuldstændig sikkerhed. Men for hvert af dem kan man give ”statistiske svar” – dvs. svar, som er baseret på data om vejret, og som ud fra modeller kan give mere eller mindre sikre overslag eller estimater.

Lad os fx tage nedbøren: modellen kan angive, at der mellem kl. 11 og 12 i morgen er 60% sandsynlighed for, at det regner på en bestemt lokation. I følge forudsigelsen er det altså muligt – endda overvejende sandsynligt – at der i det angivne interval vil komme regn. Men det er ikke sikkert, og altså heller ikke umuligt.

I almindelighed måler vi muligheden for, at en begivenhed indtræffer, som et tal mellem 0 og 1 (eller mellem $0\%$ og $100\%$, som er det samme, idet $x\%=\frac{x}{100}$). Vi kan afbilde dette mulighedsrum som i nedenstående figur, hvor der også er indsat andre almindelige ord, som de forskellige ”mulighedsmål” ofte betegnes med.

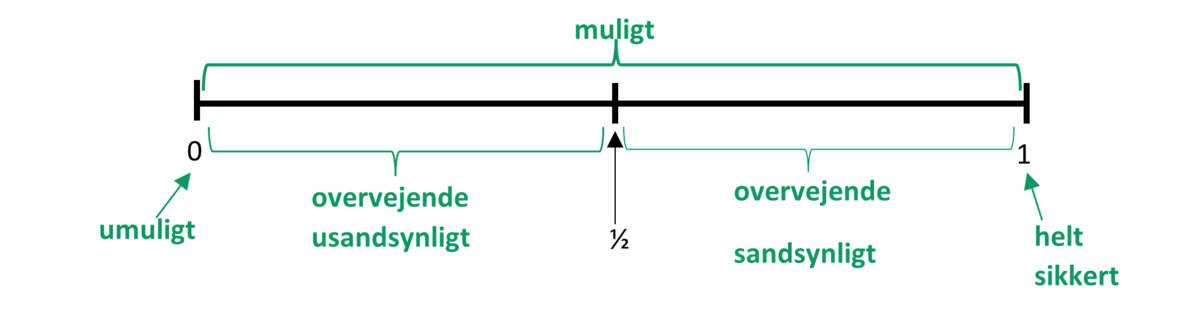
Sandsynlighed eller mulighed målt som et tal mellem 0 og 1.

I nogle tilfælde kan det være tilstrækkeligt at vide, om sandsynligheden er større eller mindre end $\frac{1}{2}$, fx hvis vi har bestemt os for at vædde 100kr på spørgsmålet om regnvejr mellem 11 og 12, og det kun drejer sig om at vælge, om man skal vædde på regnvejr eller tørvejr. Men hvis det drejer sig om større beløb, og man kan vælge at vædde eller ikke vædde, vil man nok gerne vide lidt mere.

Sandsynligheden 60% eller 0.6, som angivelse af ”muligheden for at der kommer regn mellem 11 og 12”, er klart mere præcis, end at ”det er overvejende sandsynligt, at der kommer regn mellem 11 og 12”. Teoretisk set afspejler tallet 0.6 her et lidt indviklet udsagn: hvis vi kunne observere et stort antal dage med præcis de betingelser, som den pågældende dag har i følge modellen, så ville det regne mellem 11 og 12 i 60% af observationerne. Bag ved dette udsagn ligger selvfølgelig ikke et sådant stort antal observationer af regnvejr på dage med præcis samme betingelser, som den pågældende dag forudsiges at have, men mere indviklede modeller.

Vejret er selvfølgelig blandt de mere indviklede fænomener, vi kan arbejde med. I skolen arbejder vi ofte med meget simplere ”opgaver”, fx vedr. udfald af terningkast eller børnefødsler. Men det underliggende grundbegreb er stadig som i figuren ovenfor. Hvis vi kaster to terninger, kan vi bestemme sandsynligheden for at få to seksere som $\frac{1}{36}$. Bagved denne udregning ligger flere antagelser: for hver terning er der 6 mulige udfald, som kan opstå i vilkårlige kombinationer $(x,y)$ hvor $x$ og $y$ er et af tallene 1,2,3,4,5,6; alle disse $6⋅6=36$ kombinationer er lige sandsynlige, og kun én af dem svarer til ”to seksere”. At de 36 kombinationer er lige sandsynlige betyder, at de i et meget stort antal kast med to terninger vil forekomme nogenlunde lige ofte; to seksere vil derfor optræde i ca. $\frac{1}{36}$ af det store antal kast. Vi kan selvfølgelig sige, at to seksere i et givet kast er ”overvejende usandsynligt”, men tallet $\frac{1}{36}$ giver mere præcis information.

Man skal her lægge mærke til, at sandsynligheder kan udregnes på tre måder:

På basis af observationer (helst et ”stort” antal)
På basis af en teoretisk model
På basis af en teoretisk model og observationer.

De to første er mest almindelige i skoleopgaver, og illustreres godt af eksemplet med terningerne; i virkelighedens verden har vi ofte brug for 3., som det fx er tilfældet med vejrudsigter. Vi giver nu et simplere eksempel.

Hvis vi tager en tilfældig familie med 2 børn, hvad er så sandsynligheden for at begge er piger? Den teoretiske model, man kan bruge, bygger på den antagelse, at et tilfældigt barn med en sandsynlighed $p$ er en pige, og at der ingen sammenhæng er mellem kønnene på to børn (selvom de er født i samme familie). Sandsynligheden for 2 piger blandt 2 børn er da $p^2$. Tallet $p$ bestemmes vha. af et stort antal observationer, fx andelen af piger blandt nyfødte i Danmark i 2014 (https://babyinstituttet.dk/statistik-fodsler), som er omkring 48%. Vi kan på basis heraf anslå p til at være 0.48, og får at svaret på det oprindelige spørgsmål er $0.48^2=0.23$. Vi vil på baggrund heraf forvente, at hvis vi ser på et stort antal familier med to børn, vil 23% af dem have to piger.

Det er vigtigt at forholde sig kritisk til selv simple ”opgaveløsninger” som den netop skitserede. Kan man fx uden videre regne med at andelen af piger blandt børn er uafhængig af børnenes alder? Betyder det noget, at enæggede tvillinger altid har samme køn? Find selv på flere mulige svagheder og overvej, om det er væsentligt i undervisningen at tage sådanne spørgsmål op – og om man kan gøre det uden at give det indtryk, at modeller af denne type er helt ubrugelige, for det er de bestemt ikke.

Til slut en generel bemærkning: ligesom i den øvrige matematikundervisning er det også ifm. stokastik naturligt at inddrage værktøjsprogrammer. Eksemplerne i dette tema giver enkelte forslag. Det vil føre for vidt her at give en udtømmende beskrivelse af programmer, som er relevante på de forskellige niveauer, og den ville også hurtigt blive forældet. Særlig ifm. statistik er værktøjsprogrammer i dag helt uundværlige. Som lærer bør man dog huske at de netop er værktøjer, og at brugen af dem hverken er et mål i sig selv, eller en slags magisk genvej til elevernes mestring af centrale ideer. Men værktøjerne kan, når de bruges rigtigt, hjælpe eleverne til at udfolde og udvikle deres indsigt i de centrale ideer. Fokus i dette tema er derfor på disse!