Kom i gang med positionssystemer i undervisningen
Det kan være en god idé at kombinere undervisning i positionssystemer med undervisning i det metriske system. Se hvorfor, det er vigtigt at få styr på enhederne, og eksempler fra undervisningen, der tager udgangspunkt i hverdagen, som fx nyheder om udregning af smittetal, og om hvordan vi anvender tal forskelligt i dagligdagssprog og i vores fag.
Hvordan starter man?
I erhvervsuddannelserne kan det være en fordel at undervise i positionssystemet i kombination med undervisning i det metriske system.
Det kan vække nogle elevers nysgerrighed, hvis læreren fx påstår, at 470 = 4,70.
Det er rent talmæssigt noget sludder, men sætter man enheder på, kan det blive rigtigt, fx 470 cm = 4,70 m og 470 cl = 4,70 l.
Hvilke specifikke metriske systemer man tager udgangspunkt i, afhænger af de enheder, man bruger i faget. I forskellige fag er der endvidere forskellige krav om præcision, hvor man med fordel kan have en dialog med faglærerne om niveauet.
Hvilke enheder er relevante?
I grundskolen har eleverne for første gang lært om positionssystemet. For nogle elever kan det være en hjælp at få repeteret nogle af disse grundlæggende egenskaber, det kan være ved at bruge penge som eksempel.
Også i hverdagens gøremål og i medierne og i organiseringen af praktikperioder (løn, tid mm.) møder eleverne forskellige enheder på tal, som kan være meget anvendelige som relevante eksempler på positionssystemet.
Man kan komme i gang ved at tale med eleverne om, at de i deres profession kan møde tegninger, hvor måleenheden er anderledes. I dag møder de målangivelser i tommer, både i professionen og fx til angivelse af størrelse på TV-skærme.
EUD-elever skal ud i en profession, hvor det er helt afgørende at kunne forstå/aflæse tal med enheder, omregne til andre enheder og kommunikere om størrelserne og forbindelsen mellem de forskellige enheder. Fx skal en tømrer kunne aflæse en arkitekttegning. I dag tegnes med angivelse af længder i mm, mens ældre tegninger ofte anvender cm som grundlæggende længdeenhed. Det er vigtigt, at eleverne kan vurdere, hvornår hvilke enheder er relevante, og lærerne må udpege det mest relevante for faget og diskutere med eleverne, på hvilket grundlag man kan foretage en sådan vurdering.
Titalssystemet er centralt
Centralt i arbejdet med positionssystemer er titalssystemet, og måske skal man begrænse sig til det – men det afhænger også af eleverne. Som voksne er de fleste blevet vant til titalssystemet. Vi tænker ikke altid over det. Vi bruger det fx når det drejer sig om penge eller målinger af længder og tid. Og det går som regel nemt – uanset om man kan huske begreberne 'positionssystem' og 'pladsværdisystem'.
Få flere idéer til, hvordan man kan tale med eleverne om de vigtigste positionssystemer og deres oprindelse i artiklen: Hvad er et positionssystem?
Anvend eksempler fra hverdagen
Det er vigtigt, at man bruger eksempler fra en praksis (erhverv eller hverdag) og ikke kun arbejder abstrakt med positionssystemet.
Uanset erhverv skal eleverne indgå som samfundsborgere og kunne bedømme og tage stilling til et hav af forskellige problemstillinger, og her er matematik tit et redskab. Fx er matematik et redskab i kommunikation om og forudsigelser af udvikling af COVID19-pandemien. Også her spiller forståelse af positionssystem en stor rolle. Find fx eksempler fra aktuelle nyheder i aviser og hjemmesider, hvor forskellige former for tal og størrelser er anvendt, og spørg eleverne om, hvad de betyder, og hvordan man kan forholde sig til dem.
Eksemplerne nedenunder er tænkt som inspiration til materialer, man kan anvende i undervisningen, de konkrete eksempler egner sig ikke nødvendigvis for alle typer elever eller alle professioner.
Eksempel: Betydning af matematisk notation i nyhed om COVID-19
Dette eksempel kan bruges til at snakke med eleverne om betydningen af matematisk notation.
Under COVID19-pandemien fandt man i efteråret 2020 en britisk mutation, kaldet 'cluster B.1.1.7.
Hvad betyder punktum her? Er det et engelsk komma? Det er det ikke – i al fald ikke i den betydning, man bruger i positionssystemet. Det er en biologisk/medicinsk teknisk navngivning af det, man populært kalder for 'den britiske mutation' af corona-virus. Navngivningen henviser til, hvor i virusstammens genom, der er afvigelser fra grundstammen.
Medierne viste 19. januar 2021 et eksempel på, hvordan man udregner kontakttal for den britiske mutation. Der står, at princippet er 'enkelt', hvilket nok er en tilsnigelse: (Kilde 1)

Heri indgår udregning med multiplikation af decimaltal ud over en forståelse af regnearterne hierarki. Aktuelle eksempler som COVID-eksemplet kan motivere elever til at forstå positionssystemet og multiplikation.
Hvad er 4,7 dage?
Noget 'pudsigt' i eksemplet er angivelsen af 4,7 dage. Hvad mener man med det?
Det er ikke sikkert, eleverne selv bemærker, at der er noget mærkeligt her. Men artiklen bruger et base 10-positionssystem til at angive dage, som er opdelt i 24 timer, altså faktisk base 24. Hvad betyder 4,7 dage egentlig?
Mere specifikt: Hvad er 0,7 dag? Hvor mange timer ind i det næste døgn drejer det sig om?
Det kan udregnes på forskellige måder, og man må vurdere, hvad der passer bedst til ens elever:
- $7/10 = x/24$. Find $x.$
Dvs. $24 ⋅ 0,7 = 16,8.$ Altså 16 timer og 8/10 minut. Minutter er i base 60, så vi udregner: - $8/10 = y/60.$ Find $y.$
Dvs. $60 ⋅ 0,8 = 48.$ Ingen rest. - Eller i kortere form: 0,7 brugt af et døgn som er 24 timer.
Dvs. $24 ⋅ 0,7 = 16,8.$ Samme resultat.
I dette eksempel behøver vi ikke udregne sekunder, som også er base 60.
- 4,7 dage er det samme som 4 dage, 16 timer og 48 minutter. Hvordan skriver man det?
- Det kan være:
- 16:48:00
- (16t 48′ 0″), med t som time.
På engelsk vil man bruge h for hour.
I artiklen om cluster B.1.1.7 udregnes kontakttallet sådan:

(Kilde 1)
Som lærer kan man tale med eleverne om, hvad det vil sige, at noget er 74 procent mere end noget andet.
Og bemærk at procent er angivet med ord og ikke med det matematiske symbol %.
Det er også vigtigt at vide, at matematiske notationer i praksis kan variere, fx at multiplikation som her kan angives med asterix/stjerne $*$ og ikke altid en prik $⋅$. Det kan være anderledes, end det man ser i lærebogsmaterialer og give anledning til en bredere diskussion af matematiske notationer og fagsprog i skole sammenlignet med hverdagssprog.
I eksemplet ses at matematikken i høj grad indgår i medierne, men at journalister ikke er stringente i deres matematiske notation, hvilket kan være udfordrende for mange elever.
Eksempel: Tal i nyhederne; numerisk, i ord og i metrisk anvendelse
Tal bliver angivet både numerisk og med ord, nogle gange har vi slang for ordene, og nogle gange betyder ordene ikke et konkret tal, men er en metafor.
Fx i udtrykket 'Tusind tak'. Vi mener ikke 1.000 tak i bogstavelig forstand, men 'mange tak, og sikkert mere end 'mange', fx ’rigtig mange tak'.
Vi ser ofte, at tal som tusind ikke bliver angivet numerisk, men i ord.
Fx i det kendte eventyr 'Tusind og én nats eventyr'. Dette kunne også skrives 1001, men det gør vi som regel ikke.
Heller ikke i salmen 'Du, som mætted tusind munde' er tallet angivet numerisk.
I medierne er tallene heller ikke altid angivet numerisk. I en nyhed skriver 'Køge Kyst', at Stationspladsen i Køge har fået ny belægning. (Kilde 2)
Overskriften er:
'10 tusind tons sten lagt med håndkraft'
Dette er en kombination af tal angivet numerisk (10), med ord (tusind) og en vægtenhed (tons). Hvor mange sten drejer det sig om? Det står der faktisk ikke noget om – kun hvad de vejer. 10.000 tons, dvs. 10.000.000 kg. 10 millioner kg.
Hvad er lettest at forstå? Det kan være noget, man som lærer diskuterer med eleverne, eller give dem mulighed for at diskutere det indbyrdes.
Tænk også fx på udtrykket 'mega stort'. Betyder det noget meget stort, eller betyder det $10^6$?
Nogle gange er talord brugt i medierne på en måde, som ikke giver matematisk mening. Fx denne artikel fra hjertevagt.dk, der beskriver en mand, som fik hjertestop men som nu er kommet sig. (Kilde 3)
Overskriften er:
'Tommy fik hjertestop: Jeg er tusind procent tilbage'
Procent betyder 100-del, så 1.000% er faktisk $1000/100 = 10$, hvilket ikke giver mening. Vi forstår dog fuldt ud, at meningen med sætningen er, at Tommy er kommet sig fuldstændigt.
Discountkæden Rema 1000 bruger derimod det numeriske tal i sit navn. Hos dem refererer 1000 i øvrigt til, at man kun vil tilbyde op til 1000 forskellige produkter.
Eksempel: Praktiske illustrationer af et positionssystem
Lad os se på eksempler på tal i det pladsværdisystem, vi bruger i dag: 127 og 712. Symbolerne 1, 2, 7 betyder vidt forskellige ting i de to tal. I det ene tal hentyder fx 7 til 7 1’ere (altså 7) og i det andet som 7 100’ere (altså 700). Det er, fordi vi har et titalssystem, hvor hver plads er forhåndsreserveret til en bestemt potens af 10.
Eksempel på 98.541:
| Titusinder | Tusinder | Hundreder | Tiere | Enere |
|---|---|---|---|---|
| $10^4 = 10 ⋅ 10 ⋅ 10 ⋅ 10 = 10.000$ | $10^3 = 10 ⋅ 10 ⋅ 10 = 1.000$ | $10^2 = 10 ⋅ 10 = 100$ | $10^1 = 10 = 10$ | $10^0 = 1$ |
| $9$ | $8$ | $5$ | $4$ | $1$ |
Der er i Danmark konsensus om at sætte punktum efter tusinder. I fx USA sætter man komma efter tusinder i stedet for punktum, dvs. 98,541.
Romertal
I romertallene skriver man 127 som CXXVII. Da C = 100, X = 10, V = 5 og 1 = 1 er dette tal: $ 100 + 10 + 10 + 5 + 1 + 1 = 127$. Selvom der også er konventioner på, hvordan man skriver romertal, fx at det største tal skal stå til venstre, på nær når det trækkes fra, så er dette ikke et positionssystem, da fx X altid betyder 10.
Eleverne har sandsynligvis set eksempler som disse i skolen.
Anvend konkretmaterialer
En anden måde at forklare det på er gennem konkretmaterialer som træklodser eller andet fra praksis, som kan være et pædagogisk hjælpemiddel til regning, herunder 10’er-overgange og veksling:
(Kilde 4)
Eleverne kan opbygge deres talforståelse ved at bygge tal, udføre regnestykker ved at arbejde med brikkerne, samle dem, skille dem ad osv. 10 enere kan veksles til en tier, osv. Dette er en illustration af 'mente' (tidligere kaldt 'låne') i subtraktion.
Disse konkretmaterialer illustrerer, hvordan positionssystemet er opbygget, og at principperne er de samme uanset hvilke base man vælger sig. Med tallet fem som basis (femtalsystemet) har vi maks. 4 af hver enhed, så snart vi får den 5’te, veksler vi.
| Klods | Plade | Stav | Terning | |
|---|---|---|---|---|
| Base 10 | $10^3 = 1.000$ | $10^2 = 100$ | $10$ | $1$ |
| Base 5 | $5^3 = 125$ | $5^2 = 25$ | $5$ | $1$ |
Eksempel: Illustrationer af tallenes struktur
Tre modeller hvorpå heltal kan struktureres/illustreres:
- Linjemodel
Tallinjen kan ses skematisk som en streng med kugler eller uden kugler. Illustrationen kan hjælpe eleven til at forstå forholdet mellem det at tælle tal og talstørrelser.
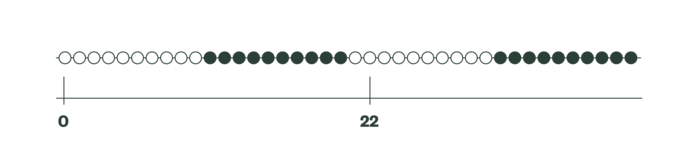
- Gruppemodel
Her er tallene strukturerede i 1’ere og 10’ere. Disse kan understøtte vekslings-princippet. Man skal dog ikke tvinge elever til at anvende disse base 10-illustrationer uden tilstrækkelig øvelse i at tælle enere og tiere. (Kilde 5)
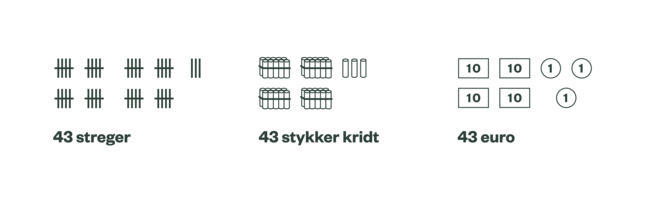
- Kombinationsmodel
Tal op til 100 kan repræsenteres på en stor abacus, en 10 x 10 kvadrat eller en 100-kant.

Eksempel: Illustration af titalssystemet
Som grundsten for alle enhedssystemer bruges metersystemet og længde. Det udbygges i en retning til areal og rumfang.
Når længde og metersystemet er forstået, er det let at hoppe over i fx vægt (gram) eller strøm (ampere). Nedenfor er vist, hvordan man billedligt kan forklare, hvordan titalssystemet fungerer:
Faktor betyder fx, hvor mange mm der skal til for at få 1 cm, eller hvor mange cm der skal til for at få 1 dm.
- Længde
Formel for udregning bliver: Længden ganget (eller divideret) med faktor 10 opløftet i antal hop.
$Resultatet = tal ⋅ 10^{antal hop}$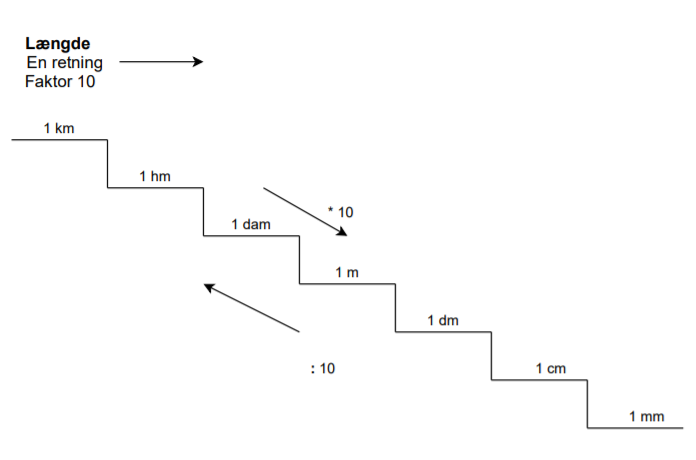
- Areal
Formel for udregning bliver: Areal gange (eller divideret) med faktor $(10^2 = 100)$ opløftet i antal hop.
$Resultatet = tal ⋅ 100^{antal hop}$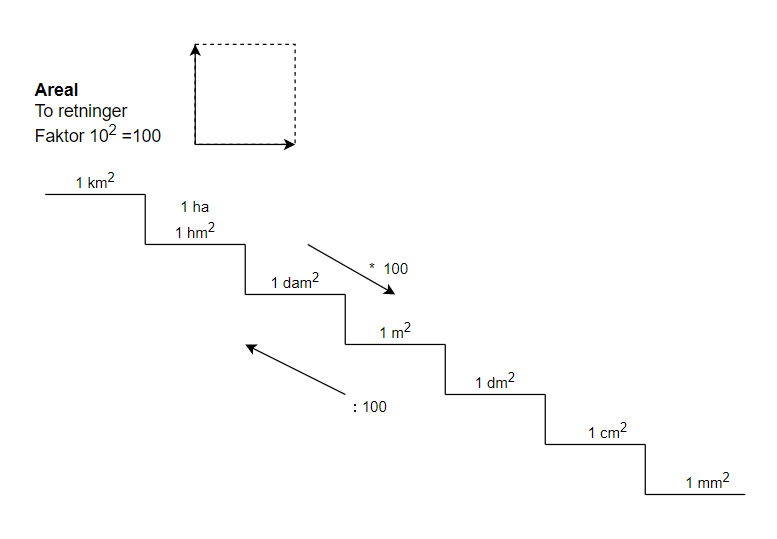
- Rumfang
Formel for udregning bliver: Rumfang gange (eller dividere) med faktor $(10^3 = 1000)$ opløftet i antal hop.
$Resultatet = tal ⋅ 1000^{antal hop}$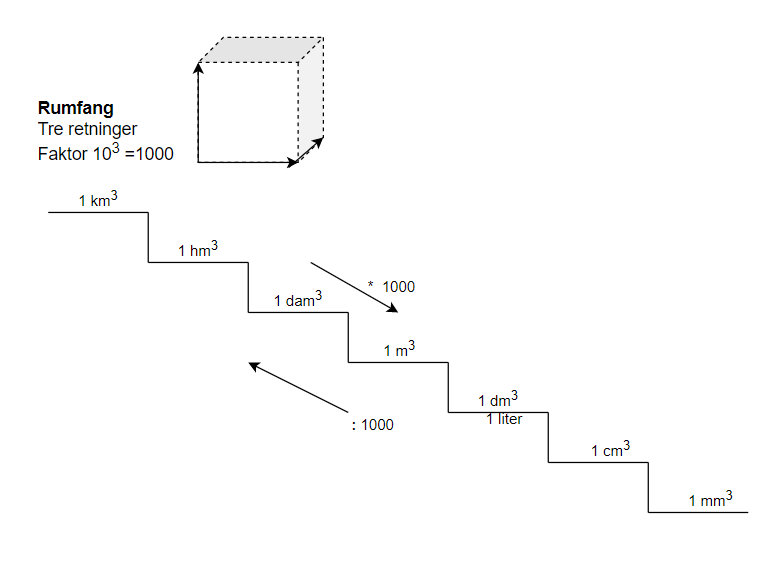
OBS: Tak til Jette Schaarup, Hillerød Tekniske Skole, for at stille de tre illustrationer til rådighed.
til: ERHVERVSSKOLER
emne: POSITIONSSYSTEMER
UDGIVET: 2021
Forfattere
Bettina Dahl Søndergaard
Lektor, ph.d. i matematikdidaktik
Aalborg Centre for Problem Based Learning in Engineering, Science and Sustainability under the auspices of UNESCO,
Aalborg Universitet/AAU
Lena Lindenskov
Lektor, ph.d. i matematikdidaktik
Institut for fagdidaktik DPU, Aarhus Universitet/AU
Lauge Sams Granerud
Faglærer
Roskilde Tekniske Skole
Kees Hoogland
Professor
University of Applied Sciences, Utrecht (IHU), Holland
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Stie, HH. (2021, januar 1). Forvirring om kontakttal for britisk mutation - sådan udregnes det. nyheder.tv2.dk.
- Køgekyst.dk (2020, maj 19). 10 tusind tons sten lagt med håndkraft, køgekyst.dk.
- Hansen I.H (2012). Tommy fik hjertestop: Jeg er tusind procent tilbage. Hjemmet.
- Breitag, T., & Venheim, R. (2005). Matematikk for lærere 2. Oslo: Universitetsforlaget
- Heuvel-Panhuizen, M. van den (2001). Children Learn Mathematics. p. 63. Freudenthal Institute, Utrecht University, The Netherlands.