Hvorfor er modellering vigtigt for matematikundervisning?
Matematiske modeller spiller en vigtig rolle i samfundet, og elever bør udvikle deres bevidsthed om dem, både med henblik på at opstille dem og med henblik på at forholde sig kritisk til dem (dette vender vi tilbage til i teksten Matematiske modeller og samfundet).
Der er flere gode grunde til at beskæftige sig med modellering i matematikundervisningen. Disse grunde har både noget med skolens brede dannelsesopgave at gøre, det har noget at gøre med undervisning og motivation, og det har meget direkte noget med matematiklæring at gøre. Der tales ofte om disse fire begrundelser:
- En pragmatisk begrundelse. Handler om vigtigheden af, at vi mennesker kan forstå, mestre og handle i situationer i den virkelige verden.
- En formativ begrundelse. Matematiske kompetencer kan fremmes ved at engagere sig i modelleringsaktiviteter; herunder både modelleringskompetencen og andre kompetencer.
- En kulturel begrundelse: Relationer mellem matematikken og omverdenen er uundværlige for at få et fyldestgørende billede af matematikkens rolle i samfundet.
- En psykologisk (en læringsmæssig) begrundelse: Eksempler fra den virkelige verden kan bidrage til at øge elevernes interesse og motivation for matematik. Samtidig kan forbindelsen til elevernes erfaringsverden støtte deres matematiske forståelse og hjælpe dem med at strukturere og huske det matematisk indhold. (Kilde 1).
I en 5. klasse har eleverne arbejdet med opgaven ”burhøns” fra www.kidm.dk. I opgaven skal elever undersøge, hvor mange burhøns der kan være på 1 m2. Hver høne fylder 1 A4 ark plus et postkort. Eleverne arbejde kan her beskrives i forhold til modelleringscyklussen. I oversættelsen fra omverdensituationen til det matematiske domæne overvejer eleverne, hvordan de kan løse denne problemstilling i klassen. I den matematiske problemløsnings-delproces arbejder eleverne forskelligt. Nogle elever ligger på gulvet og laver et slags puslespil med A4 papir og postkort, hvor de prøver sig frem og undersøger hvor mange høns, der kan være på et kvadratmeter stort stykke plastik. Andre regner sig frem til arealet af et stykke A4-papir og postkortet og dividerer efterfølgende 1 m2 med det fundne areal. I fortolkningen af deres svar er der flere, der er forbavsede over, hvor mange høns der faktisk kan være på så lille et område, og i valideringen drøftes usikkerhederne i de to udregningsmodeller fx i forhold til, at hele plastik-stykket er svært at dække med postkort og A4 papiret og hvornår kan man så være sikker på at der ikke er plads til en høne mere.
Der er flere begrundelser for at arbejde med et forløb som dette i grundskolen. For det første er der en pragmatisk begrundelse, da forløbet giver eleverne et indblik i den situation, som burhøns har i den virkelige verden
For det andet er der en formativ begrundelse for forløbet, både fordi eleverne bliver bedre til at modellere burhønssituationen, men også fordi de samtidig får arbejdet med andre matematiske stofområder som her areal og division på en naturlig og relevant måde.
For det tredje er der en kulturel begrundelse, idet eleverne igennem arbejdet med opgaven får en større forståelse for, hvordan matematik kan bruges til at opnå en mere nuanceret forståelse af verden. , her i form af burhøns’ levevilkår.
Endelig er der også en psykologisk begrundelse for opgaven, idet den lægger op til, at eleverne bliver optaget af og lever sig ind i burhønsenes livsvilkår. Opgaver som denne kan derfor bidrage til, at eleverne bliver mere motiverede for matematik.
At kunne anvende matematik indebærer mere eller mindre synlige former for matematisk modellering. Det er derfor vigtigt, at der er fokus på at udvikle elevernes matematiske modelleringskompetence i undervisningen. Modelleringskompetencen indgår derfor også i de gældende læseplaner.
Modellering som middel til matematiklæring
Arbejdet med matematisk modellering kan både være et mål i sig selv og et middel til at fremme matematikforståelse. Når man søger at udvikle elevers matematiske modelleringskompetence som et selvstændigt mål, er er der fokus på, hvordan matematik bliver bragt i anvendelse i hverdagsliv, naturforhold og samfundsliv ved at eleverne aktivt lærer at opstille matematiske modeller, lærer at anvende matematiske modeller eller lærer at være kritiske reflekterende overfor anvendelser af matematiske modeller.
Men modellering kan også være et middel til at fremme elevernes begrebsforståelser (Kilde 2). Eleverne kan blive klogere på statistik ved at anvende statistiske modeller i en bestemt situation. Mange af skolens andre fag kan desuden drage nytte af matematiske modeller og matematisk modellering. I fysik og kemi sker dette, når der fx skal regnes på kræfter og energier, men det kan også være i natur og teknologi eller i samfundsfag, hvor matematiske modeller kan indgå som middel til at blive klogere på andre fagområder.
En beskrivelse af hvordan modellering kan bruges til at fremme matematisk begrebsdannelse ses i de seks opstillede principper for oplæg til Modelfrembringende aktiviteter, som er udviklet af Lesh & Doerr (Kilde 3).
- 1. Princip - Meningsfuldhed: Oplægget i undervisningen skal lægge op til, at eleverne oplever situationens problemstilling som meningsfuld. Eleverne støttes i at forstå situationen baseret på deres egen personlige viden og erfaringer.
- 2. princip - Modelkonstruktion: Oplægget i undervisningen skal lægge op til, at eleverne kan se behovet for at udvikle en matematisk model og nytten af at forfine modellen.
- 3. Princip - Selvevaluering: Oplægget skal gøre evalueringskriterier tydelige for eleverne, så de selv kan vurdere, hvornår deres svar er gode nok.
- 4. princip - Dokumentation: Oplægget skal lægge op til, at eleverne dokumenterer deres tænkning og den matematik, der inddrages.
- 5. princip – Enkelthed: Oplægget skal indeholde en situationen så enkel som mulig, samtidig med at der skabes behov for, at der skal udvikles en model.
- 6. Princip: Generalisering: Aktiviteten skal føre til, at der kan udvikles en model, der kan være prototype for andre lignende situationer.
Eksempel på en aktivitet der lever op til de 6 principper: “The big foot problem”
I denne aktivitet arbejder elever i en udskolingsklasse med en problemstilling, der er kendt som “The Big foot problem” og er hentet fra teksten Lesh & Harel (Kilde 4).
For at gøre problemstillingen meningsfyldt for eleverne (princip 1), initerede læreren at eleverne skulle starte med at drøfte, hvorfor indfødte amerikanere i gamle dage var gode til at følge spor. De indfødte kunne ud fra fodspor se, hvor tunge personerne der satte fodsporene var, og hvor hurtigt de bevægede sig. Efter denne diskussion blev den egentlige problemstilling introduceret og iscenesat af læreren: ”Byens statue har være i stykker et stykke tid, men i nattens løb er den blevet genopbygget. Ingen ved, hvem der har gjort det, men reparatørerne har afsat nogle fodspor og nu ønsker byrådet meget gerne at vide hvem der reperarede statuen, så de kan takke dem”. Disse fodspor har eleverne nu adgang til, og myndighederne vil i første omgang gerne vide, hvor høje personerne er. Eleverne får samtidig udleveret et fodaftryk (se figur x), og opgaven er nu, at eleverne skal udarbejde en slags “værktøjskasse”/tilgang, som politiet kan bruge til at finde ud af, hvor store personerne er ud fra deres fodaftryk.
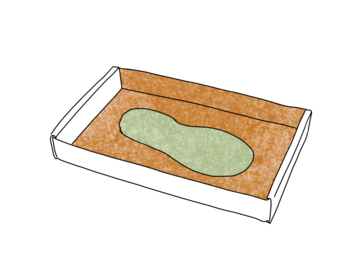
Eleverne skal nu i gang med at konstruere en matematisk model (princip 2), der kan hjælpe dem med at se sammenhængen mellem skostørrelse og højde. Der er mange overvejelser i dette. Hvad gøres der ved den store forskel, der ofte er på kvinder og mænds skostørrelser? Hvilke variable kan der ændres på osv. Den matematiske model kan forfines på mange forskellige måder.
Eleverne kan validere deres matematiske model udfra empiriske kriterier (princip 3). Eleverne kan fx ved hjælp af stikprøver af andre personers højde og skostørrelse undersøge, om deres model holder. Holder modellen stadig, hvis andre data blev indsat?
Eleverne dokumenterer (princip 4) deres arbejde. De skal forsklare deres arbejde med at undersøge hvor stor personen, der lavede fodtrykket, kunne have været. En gruppe fremstillede denne model (figur 3.2).
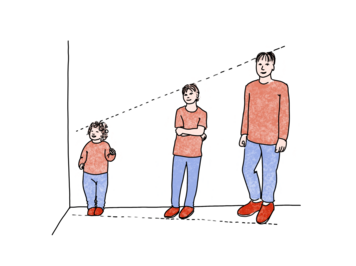
Her, prøv dette... Stil dig op ved væggen... Sæt hælene her mod væggen... Ben - stå her. Frank, stå her... Jeg vil stå her, fordi jeg er omtrent den samme (størrelse) som Ben. [Hun peger på et punkt mellem Ben og Frank, der er noget tættere på Ben]... [pause]…Nu, okay, hvor skulle den person [the big foot] være? – Hmmm. [Hun tegner en linje, der passerer lige foran deres tæer.]… Derovre, tænker jeg. Ok. … [Hun peger på en position, hvor tæerne på alles sko ville danne en ret lige linje.]
Ovenstående beskrivelse viser, hvordan eleverne udvikler en simpel model (princip 5) for sammenhængen mellem skostørrelse og personers højder. Der er ikke langt fra, at denne model kan være en prototype for andre lignende situationer, som evt. kunne kan handle om en lineær sammenhæng eller proportionalitetsbegrebet (princip 6).
Spørgsmål til fagteamet
- Hvilke erfaringer har I med at arbejde med modellering som middel til at få en større forståelse for fx matematiske begreber? Hvorfor valgte I at arbejde med modellering for at opnå denne forståelse?
- Overvej, hvordan I kan lave et forløb eller aktivitet, der får eleverne til at arbejde med modelfrembringende aktiviteter, der lever op til de 6 principperne for oplæg til Modelfrembringende aktiviteter beskrevet af Lesh & Doerr?
til: GRUNDSKOLE
emne: MODELLERING
UDGIVET: 2023
Forfatter
Dorte Moeskær Larsen
Lektor, ph.d.
UCL Erhvervsakademi og Professionshøjskole
Morten Misfeldt
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Blum, W. (2015). Quality teaching of mathematical modelling: What do we know, what can we do?. In The proceedings of the 12th international congress on mathematical education (s. 73-96). Springer, Cham.
- Niss, M., & Højgaard Jensen, T. (red.) (2002). Kompetencer og matematiklæring: ideer og inspiration til udvikling af matematikundervisning i Danmark, København: Undervisningsministeriets forlag. (Uddannelsesstyrelsens temahæfteserie; Nr. 18).
- Lesh, R., & Doerr, H. M. (2003). Foundations of a models and modelling perspective on mathematics teaching, learning and problem solving. In Lesh, R., & Doerr, H. M. (Eds.) Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning, and Teaching (pp. 3-34). Mahwah, NJ: Lawrence Erlbaum Associates, Publishers.
- Lesh, R. & Harel, G. (2003). Problem Solving, Modeling, and Local Conceptual Development, Mathematical Thinking and Learning, 5, 157-189, DOI: 10.1080/10986065.2003.9679998
- Blomhøj, M., & Kjeldsen, T. H (2010). Mathematical modelling as goal in mathematics education – developing of modelling competency through project work. I: Sriraman, B. et al., The first sourcebook on Nordic research in mathematics education (s. 555-568). Information Age Publishing
- English, L.D., Watters, J.J. Mathematical modelling in the early school years. Mathmatics Education Research Journal 16, 58–79 (2005). doi.org/10.1007/BF03217401