Modellering og model – proces og produkt
Matematisk modellering er processer, hvor matematik anvendes til at beskrive situationer og løse problemer fra verden omkring os (Kilde 1). Grundskoleelevers arbejde med matematiske modeller kan både bestå i at frembringe matematiske modeller og i at analysere og forholde sig kritisk til egne eller andres matematiske modeller.
Dette tema beskriver dels, hvad en matematisk model er, og dels hvordan elever kan arbejde med at frembringe, analysere og kritisere matematiske modeller.
Et eksempel på matematisk modellering

En gruppe mellemtrins-elever undersøger, hvordan grundplanen for et hus kan se ud, hvis dets beboelsesareal skal være præcis 120 m2. Eleverne overvejer betydningen af grundplanens geometriske form. Skal huset være rektangulært, eller skal det have en L-form? Eller måske være rundt? Skal huset være i flere etager?
Eleverne udvikler matematiske beskrivelser af husets grundplan. De bruger, hvad de ved om geometri og målestoksforhold til at beskrive huset. Efterfølgende diskuterer de, om grundplanerne passer til omverdenens krav (fx tilgængelige byggematerialer og typiske former på byggegrunde). Dermed tager de stilling til løsningernes kvalitet.
I modelleringsprocessen bevæger eleverne sig frem og tilbage mellem den konkrete omverdens-situation i form af den konkrete grundplan for huset og matematikken i form af den geometriske beskrivelse af husets grundplan og arealformler
Hvad er en matematisk model?
En matematisk model er en beskrivelse af et udsnit af verden (eller en forestillet virkelighed), der konstitueres af tre elementer; objektet for modellen, modellens matematiske repræsentation samt den indbyrdes relation (eller oversættelsen) imellem objektet og repræsentationen (Kilde 2). Den matematiske model beskriver således en relation mellem udvalgte træk ved virkeligheden og den matematik (fx en formel eller en algoritme), der indgår i modellen. Et vigtigt aspekt ved denne definition er, at modellen altid er en relation, der repræsenterer nogle og ikke alle aspekter af virkeligheden (Kilde 2). Derfor er der altid et informationstab og en mulighed for fejl-repræsentation af virkeligheden, når man gennemfører matematisk modellering.
Matematiske modeller kan anvendes til forskellige formål. En model kan bruges til at beskrive fænomener i den virkelige verden. Hvis man fx ønsker at undersøge om der er en sammenhæng mellem sønner og fædres højde og man har et datasæt over deres højder, kan man forsøge at lave en deskriptiv model over sammenhængen imellem disse størrelser. Viser en lineær regression, at sønnernes højde afhænger af fædrenes, så er den resulterende lineære sammenhæng inklusive funktionsforskrift en model. Men modeller kan også bruges til at forudsige fremtidige begivenheder – for eksempel kan ovenstående bruges til at forudsige en søns højde ud fra faderens højde.
Eksempel på elever der skaber matematiske modeller (udskoling):
I forløbet ’Matematikmorgener’ (Kilde 3) arbejdede elever i 8. klasse med at beskrive situationer fra deres omverden med matematiske modeller. Flere elever valgte at beregne, hvor meget vand de brugte til deres bad om morgenen. Eleverne forsøgte på forskellige måder at måle, hvor meget vand der løb ud af bruseren. En af eleverne valgte eksempelvis at holde en gulvspand ind under bruseren i et minut og bagefter måle, at der var 6 liter vand i spanden. Eleven udregnede derefter, at når han badede om morgenen i 10 minutter, så brugte han i alt 63 liter vand, idet han først lod vandet løbe i 30 sekunder, indtil vandet fik den ønskede temperatur (3L) og derefter selv stod under vandet i 10 minutter (60L). Læreren ville derefter høre, om eleven kunne lave en tabel, der viste, hvor meget vand han brugte alt efter, hvor lang tid han badede. Kort efter havde eleven lavet en tabel, der viste vandforbruget for 1-20 minutter. Læreren udfordrede nu eleven til at lave en graf i et koordinatsystem.
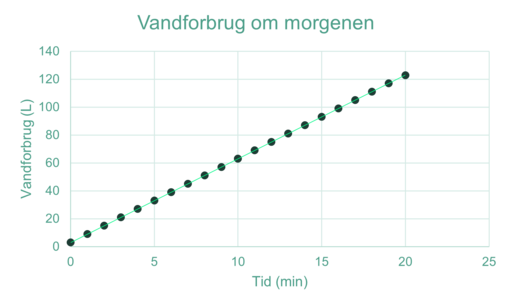
Eleven kom nu frem til modellen vist i figur 1.2. Læreren efterspurgte derefter en formel, der kunne beregne vandforbruget. Efter nogle minutter og lidt hjælp fra læreren, nåede eleven frem til, at $y= 6x+ 3$ kan beskrive vandforbruget (y) som funktion af tiden i badet (x).
I dette forløb veksler eleven mellem at være i ’matematikkens verden’ og ’den virkelige verden’ (jf figur 1.1) og ender med at opstille en formel, der beskriver sammenhængen mellem vandmængde og tid under bruseren. Modellen består af tre elementer (jf figur 1.1); en matematisk repræsentation, som her er forskriften for funktionen
Spørgsmål til fagteamet
- Hvilke erfaringer har I med at arbejde med matematisk modellering på forskellige klassetrin?
- Prøv at give eksempler på matematiske modeller, som eleverne har arbejdet med i undervisningen.
til: GRUNDSKOLE
emne: MODELLERING
UDGIVET: 2023
Forfatter
Dorte Moeskær Larsen
Lektor, ph.d.
UCL Erhvervsakademi og Professionshøjskole
Morten Misfeldt
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Niss, M. & Jensen, T. H. (2002). Kompetencer og matematiklæring – ideer og inspiration til udvikling af matematikundervisning i Danmark. Uddannelsesstyrelsens temahæfteserie nr. 18. København: Undervisningsministeriet.
- Blomhøj, M. (2006). Mod en didaktisk teori for matematisk modellering. I O. Skovsmose og M. Blomhøj (red.) Kunne det tænkes? – om matematiklæring, København: Malling Beck, 80-109.
- Blomhøj, M. og Skånstrøm, M. (2006): Matematikmorgener, i Skovsmose, O. og Blomhøj, M. (red.), Kunne det tænkes? – om matematiklæring, s. 7-23, København: Forlag Malling Beck.