Matematiske modeller og samfundet
Matematiske modeller har en central betydning i vores samfund. Tænk for eksempel på den rolle, som modeller spiller i krisehåndtering. I Coronakrisen hørte vi alle om “den grønne kurve” og “den røde kurve”, og om begreber som “kontakttal” og “positivprocent. (se også temaet Epidemimatematik) Dem, der udviklede modeller over smittespredning, havde meget stor betydning for vores dagligdag.
I en skolekontekst kan Corona-krisen behandles gennem agentbaseret modellering, hvor en hel masse virtuelle agenter, udstyret med forprogrammerede egenskaber, interagerer. Agenterne kan repræsentere mennesker, molekyler, fugle eller alt muligt andet (Kilde 1).
I figur 4.1 ses et eksempel på, hvordan man i grundskolen kan arbejde med agentbaseret modellering i forhold til Corona-krisen gennem programmet StarlogoNOVA.
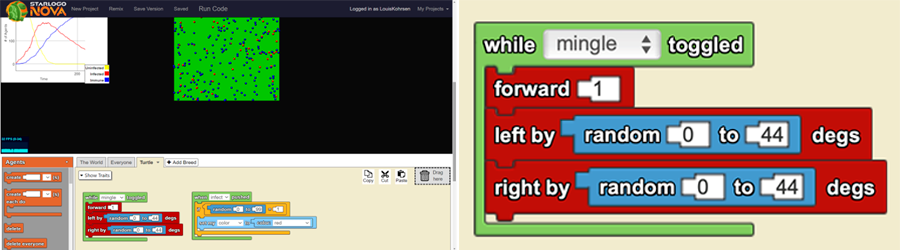
StarlogoNOVA er et blok-programmeringssprog til agentbaseret modellering. I StarlogoNOVA programmeres en masse agenter, der bevæger sig efter nogle fastlagte regler. På figur 4.1 ses programmet køre en epidemimodel, hvor alle agenterne (her gule, røde og blå bolde) bevæger sig rundt på en grøn skærm, i tilfældig retning. Programmet tæller, hvor mange røde, blå og gule bolde der er i det grønne felt og skriver antallet i grafen til venstre
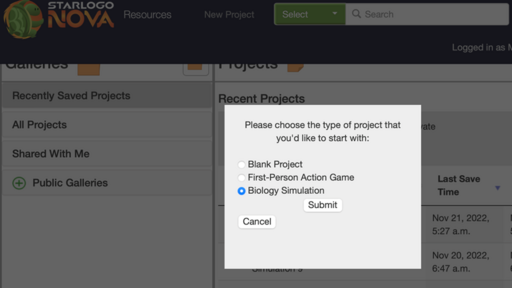
StarlogoNOVA har allerede en forprogrammeret-epidemimodel, som man kan bruge som udgangspunkt, herfra kan modellen rettes til og parametre ændres. I modellen skal de gule indikere raske personer, de røde smittede personer, og de blå immune personer.
Agentbaserede modeller gør det muligt at arbejde med hypotetiske scenarier, og de er begrebsmæssigt mere tilgængelige end modeller, der fx bygger på differentialligninger.
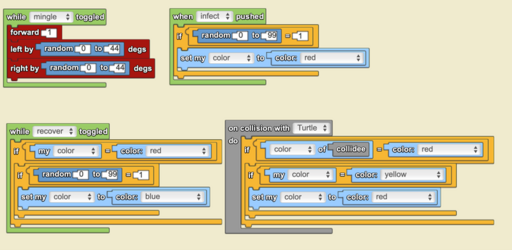
Arbejdet med denne model gør det meget enkelt at træne oversættelsen til virkeligheden. Hvad betyder det, at en agent skifter farve? Kan vi anvende nogle af de tiltag, vi brugte under Corona-epidemien til at mindske udbredelsen i modellen? Hvordan vil vi fx repræsentere hel eller delvis samfundsnedlukning? Eller maskepåbud?
At undervise med star logo nova
Et undervisningsforløb i udskolingen om epidemier kan for eksempel starte med, at eleverne starter programmet og går til den pre-installerede epidemimodel. Derefter kan de undersøge programmet og prøve at finde ud af, hvad de forskellige dele af programmet gør.
I første omgang kan eleverne beskrive outputvinduerne (figur 4.1 øverst). Hvad sker der, som tiden går?
For at støtte eleverne i at forstå modellen, kan læreren bede dem forklare de fire scripts, der styrer agenternes bevægelser.
Eleverne kan herefter undersøge fanebladet ”the world”. Hvor mange agenter er der med i simulationen? Starter de som raske eller syge agenter? Hvordan genereres graferne?
De kan sammenligne de grafer, de får ud af at køre programmet (figur 4.1 øverst til venstre). De kan opdage, at graferne ikke er helt ens på trods af, at de alle har startet simulationen med de samme parametre. Hvorfor det?
De kan derefter forsøge at genskabe centrale diskussionspunkter om samfundsaktivitet og smitteoverførsel. Kan I modellere håndsprit, nedlukning og masker? Disse løsninger er det oplagt at fremlægge for hinanden i klassen.
Endelig kan arbejdet understøtte en diskussion af det forhold at den tilfældighed, der er indbygget i simulationen, gør, at de samme parametre kan give anledning til forskellige opførsler.
Perspektiver på matematiske modeller og kriser
Matematiske modeller og samfundskriser er tæt forbundet. Den danske matematikdidaktiker Ole Skovsmose beskriver i Mathematics and crises (Kilde 2) tre forskellige sammenhænge mellem matematiske modeller og kriser.
(1) Matematiske modeller kan bruges til at holde øje med og vurdere kriser.
(2) Matematiske modeller kan bidrage til at skabe kriser.
(3) Matematiske modeller kan i nogle tilfælde være den eneste adgang, vi har til at se og vurdere kriser.
Gode eksempler på (1) er coronakrisens kontakttal og positiv procent, som blev brugt til at vurdere pandemiens alvor. Et andet eksempel er måltal for økonomisk ulighed (ginikoefficienten)
At matematiske modeller kan bidrage til at skabe kriser (2) kan virke sært, men i nogle tilfælde påvirker den matematiske model verden meget direkte og kan være med til at give anledning til en krise. Her fremhæver Skovsmose den økonomiske krise i 2008, hvor den matematiske formel, Black-Scholes formel, kan ses som det, der muliggjorde handlen med aktieoptioner og andre spekulative værdipapirer, og derfor samtidig kan anses som en aktør i den spekulation, der ledte op til børskrakket. Netop dette eksempel viser vigtigheden af den analyserende del af modelleringskompetencen, det vil sige det at udvikle en kritisk sans overfor konkrete modellers betydning for samfundet. Der er mange eksempler på politisk vedtagne modeller med samfundsmæssig betydning (fx omkring afgift og skatteberegninger), og der er en række videnskabeligt og administrativt udviklede modeller (fx omkring økonomisk fremskrivning), der har politisk betydning.
Black Scholes formel og finansielle modeller
Black Scholes formel prissætter en aktieoption, det vil sige retten til at købe en given aktie til en på forhånd fastlagt pris på et på forhånd aftalt tidspunkt ude i fremtiden. Ud fra idealiserede antagelse om at aktier udvikler sig tilfældigt, og at penge har en fast værdi, kan man beregne en unik pris for en aktieoption. Denne model gav anledning til, at der op til finanskrisen udviklede sig et relativt ureguleret marked for handel med sådanne aktieoptioner, hvilket i manges øjne var en medvirkende årsag til krisens alvorlighed.
Det sidste og tredje aspekt (3), som Skovsmose fremhæver, er, at matematik kan være den fremkaldervæske, vi bruger til at se en krise gennem. Det har langt hen ad vejen været tilfældet med klimakrisen. Vi forstår primært klimakrisen igennem modeller over temperaturstigninger, vandstandsstigninger og tørke, som er fremskrevet ud i fremtiden. De anvendte modellerne tager her ofte højde for fremtidig teknologiudvikling og usikre afledte effekter og bliver derfor meget usikre samtidigt med, at disse modeller er (og betragtes som) vores bedste bud på fremtidsscenarier, og derfor bruges de til at vurdere og legitimere forskellige beslutninger.
Klimamodeller
De modeller, der ligger til grund for forudsigelserne af fremtidens klima, er ofte simulationer af klodens klima baseret på dels fysiske sammenhænge (som tryk og temperatur) og dels på empiriske data. Modellerne er komplekse og beregningstunge, og involverer ofte, at atmosfæren over kloden deles ind i felter med fysiske egenskaber som tryk, temperatur og luftfugtighed, og den gensidige påvirkning mellem disse felter beregnes over tid. Forskellige simulationer vil derfor uvægerligt give forskellige resultater og derfor være behæftet med stor usikkerhed. Derudover er de enkelte modeller svære at sætte sig ind i, fordi de er matematisk komplekse. På den ene side er det således helt centralt at have matematisk kompetence for at deltage i en oplyst debat om klimaforandringer, og på den anden side er det ofte ikke realistisk, at grundskolematematik gør eleverne i stand til rent faktisk at udføre eller i detaljer forstå de forskellige klimamodeller.
At undervise problem- og projektorienteret med matematiske modeller
At undersøge naturen eller samfundet gennem matematik involverer altid modellering. Undervisning i og med matematisk modellering har derfor stort overlap med undersøgende undervisning (se tema om undersøgende matematikundervisning) og trækker på matematik i en tværfaglig kontekst. Projektarbejde kan være en god måde at komme i dybden med et problem, der involverer matematisk modellering. Alt efter klassetrin, klasseteamets fokusområder og elevernes interesser kan projekter for eksempel handle om epidemier med brug af StarLogo NOVA som beskrevet ovenfor, men eleverne kan også dykke ned i spørgsmål om, hvordan økonomisk ulighed måles eller sætte fokus på nogle af de modeller, der er med til at definere det økonomiske råderum i dansk politik. Der er mange muligheder, og der findes mange spændende matematiske modeller der kan udvikles eller tages udgangspunkt i når undervisningen er problem- og projektorienteret.
- Prøv at give forskellige eksempler på, hvordan matematiske modeller har spillet en rolle i elevernes hverdag.
- Hvilke erfaringer har I med at arbejde kritisk med forskellige matematiske modeller i jeres undervisning?
til: GRUNDSKOLE
emne: MODELLERING
UDGIVET: 2023
Forfatter
Dorte Moeskær Larsen
Lektor, ph.d.
UCL Erhvervsakademi og Professionshøjskole
Morten Misfeldt
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Køhrsen, L. & Larsen, D.: Agentbaseret programmering og pandemimatematik - et bud på hvordan programmeringsopgaver kan være med til at udvide matematikfaget. (ikke udgivet)
- Skovsmose, O. (2021). Mathematics and crises. Educational Studies in Mathematics, 108(1), 369-383.
- Misfeldt, M. (2022). Matematik med mening. Aarhus Universitetsforlag