Arbejdet med matematisk modellering
Arbejdet med matematisk modellering har to sider. På den ene side kan elevernes arbejde handle om aktivt at udvikle og opstille modeller, og på den anden side kan det handle om at anvende, analysere, tolke og kritisere andres matematiske modeller.
At udvikle og opstille modeller
Elevers arbejde med aktivt at udvikle og opstille matematiske modeller omtales ofte som en modelleringsproces eller modelleringscyklus, (se fx Kilde 1, Kilde 2, Kilde 3), der kan beskrives med 4 delprocesser (se figur 2.1):
- Oversættelse fra omverdensituationen til matematik hvor centrale parametre fra situationen udvælges og fastlægges. Disse oversættes til matematiske repræsentationer i en matematiseringsproces. Her formuleres også et matematisk spørgsmål eller et problem som som hvis det kan løses, bidrager til at løse det egentlige omverdensproblem.
- Den matematiske problemløsning, Matematikken anvendes her til at finde en løsning på det opstillede problem. Det er ikke altid at der er tale om egentlig matematisk problemløsning. Nogle gange er det snarere en simpel matematisk behandling (fx at sætte et tal ind i en formel) der bringer os til en løsning der kan fortolkes.
- Fortolkningen - den matematiske løsning eller det matematiske svar skal oversættes tilbage til et svar på det oprindeligt formulerede spørgsmål i omverdensituationen. (afmatematisering)
- Valideringen – handler om hvorvidt de svar den matematiske løsning tilbyder er tilfredsstillende i forhold til formålet, og om svarene er valide. Er modellen god? Giver den korrekte og brugbare svar? Hvad svarer modellen ikke på?
Arbejdet med at oversætte til matematik, handler blandt andet om at afgrænse og tydeliggøre omverdensproblematikken for at finde de centrale parametre, samt at foretage nødvendige afgrænsninger og antagelser. Det er vigtigt at afgrænse, hvilke dele af problemet der tages med i modellen, og hvilke der udelades. Det er desuden vigtigt at beskrive disse antalgelser og reflektere over dem i fortolkning og validering.
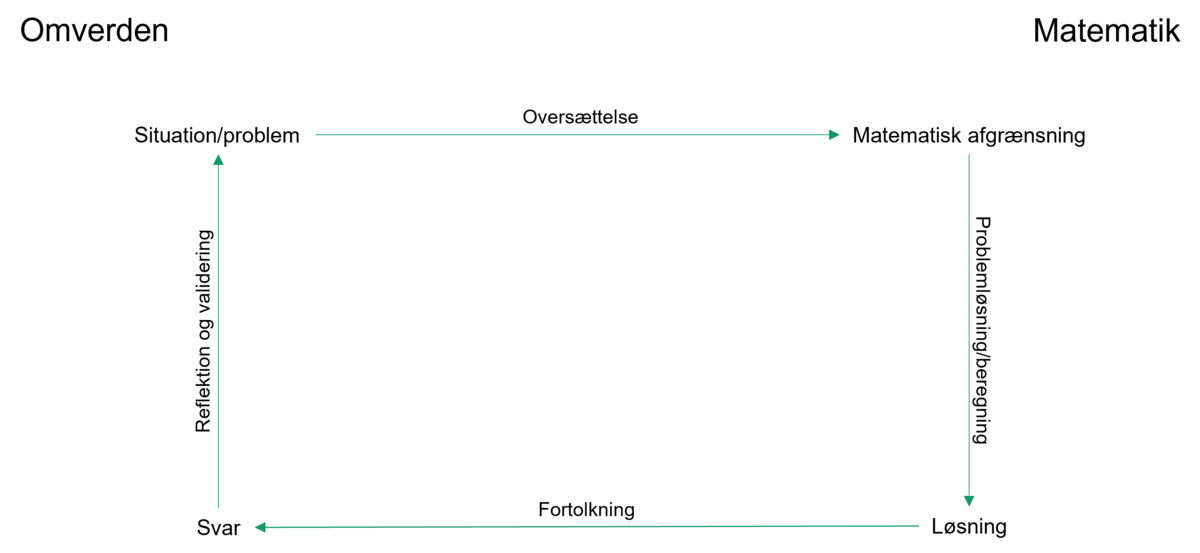
Undervejs i elevernes arbejde med at modellere er de måske nødt til at gå tilbage i cyklussen og reformulere deres spørgsmål eller forfine deres matematiske model. En matematisk modelleringsproces kan derfor ses som en cyklisk proces, der ikke har noget entydig start- og slutpunkt.
Der findes forskellige versioner af modelleringscyklussen, men modellen på figur 2.1 er hyppigt anvendt til at beskrive modelleringsprocessen, fordi den beskriver processen ret enkelt (se også Modellering i gymnasie søjlen). Dog skal det siges, at disse cykliske modeller også kritiseres for at overse vigtige aspekter af processen fordi de kommunikerer en idealiseret sekventiel strukturering af arbejdet der ikke altid passer med virkeligheden. Fx kan inddragelse af teknologi lægge et ekstra lag på modelleringsarbejdet hvor digitale simulationer kan sammenholdes med obserbationer af omverdenen i modeluydviklingsprocessen (Kilde 4).
Eleverne behøver ikke nødvendigvis at arbejde med hele modelleringsprocessen, de kan også arbejde med enkelte delprocesser af cyklussen. Ved fx at fokusere på første delproces kan eleverne arbejde med at opstille en model dvs. at lave selve matematiseringen, eller de kan fokusere på delproces 4 ved at validere og diskutere forskellige matematiske modeller.
For at understøtte at eleverne bliver dygtige til matematisk modellering, kan man starte med en simplere udgave af en modelleringscyklussen (fx figur 1.1) og gennem årene udbygge den. I indskolingen kan eleverne eksempelvis starte med at arbejde med hverdagssituationer, hvor de foretager enkelte oversættelser til matematikken. Efterhånden får de mulighed for i stigende grad at tolke resultaterne af deres matematiske arbejde i forhold til den hverdagssituation, som matematikken belyser. Undervisningen kan bl.a. give eleverne mulighed for at vurdere, om resultatet af en beregning ser ud til at kunne passe med den omverden, beregningen vedrører.
Eksempel på en modelleringsopgave til indskolingen
Eleverne får fortalt en historie om en dreng, Villiam, der skal lave en indhegning til sine kaniner ude på græsplænen. Villiam har i alt 12 meter hegn. Eleverne får nu til opgave at undersøge, hvordan Villiam kan gøre dette på en måde hvor der bliver god (fx så meget som muligt) plads til kaninerne (Kilde 5).
- Oversættelse fra omverdensituationen til matematik
Eleverne skal i denne opgave lave en simpel oversættelse fra historien, der fortælles, og til matematikkens verden, hvor eleverne skal vælge, hvordan et kaninhegn kan se ud. Hvilke former kender eleverne? Og hvad giver mening som form for et kaninhegn? I oversættelsen skal der altså tages en række valg og evt. undersøges, om der er nogle begrænsninger.
- Den matematiske problemløsning
Under den matematiske problemløsning kan eleverne undersøge, hvilke geometriske former der kan laves så hele hegnet anvendes. Eleverne kan også prøve at finde det størst mulige areal med et hegn på 12 meter.
- Fortolkningen
Efter eleverne har afprøvet forskellige geometriske former, kan de vælge, hvordan de ønsker, hegnet skal se ud. De skal i afmatematiseringen også begrunde, hvorfor de har valgt, at hegnet til kaninerne skal se således ud - er det en god form for kaninerne?
- Valideringen
Eleverne skal nu afgøre om den valgte form er tilfredsstillende i forhold til formålet med modelleringen, og om hegnets længde er 12 meter.
Eksempel på elevers modellering på mellemtrinnet
Elever i en 4. klasse kan også arbejde med hele modelleringscyklussen. Det kan de gøre fx i “Biblioteksopgaven” (Kilde 6), der handler om, at eleverne skal undersøge, hvor mange bøger der er på skolens bibliotek.
- Oversættelse fra omverdensituationen til matematik
Her må eleverne overveje, hvordan de kan undersøge dette, da det fx ikke vil være realistisk at tælle alle bøgerne. Eleverne skal derfor overveje, hvilke parametre de kan anvende, og hvilken strategi der kan hjælpe dem. Det kunne fx være at bestemme antallet af bøger på en hylde for efterfølgende at bruge regnestrategier, hvor addition eller multiplikation indgår. Det er også muligt at bruge en strategi, som bygger på måling, hvor eleverne fx tæller, hvor mange bøger der står på en meters hylde og derefter estimerer hvor mange meter hylde, der er på biblioteket. - Den matematiske problemløsning
Alt efter hvilken strategi eleverne har valgt, skal de nu til at finde og evt. beregne antallet af bøger på biblioteket. De forskellige parametre kan så enten estimeres ved et ”begavet slag på tasken” (en bog er ca. 2 cm bred), tælles eller opmåles (fx antallet af reoler) eller tælles i et udvalg (fx hvor mange bøger pr meter hylde et eller flere steder på biblioteket).
Undervejs i processen vil en del grupper måske opdage, at de er nødt til at justere deres plan. - Fortolkningen af svaret
Her skal eleverne overveje deres bud på antallet af bøger på biblioteket. Dette kan give anledning til en drøftelse af, hvornår to resultater er forskellige eller ens. Det vil ofte kun være muligt at angive et cirkatal for antallet af bøger på biblioteket, så hvordan sammenligner eleverne deres udregninger og løsninger? - Valideringen
Her kan der evt. drøftes de forskellige parametre af den anvendte model. Hvordan er antal hyldemeter udregnet? Hvor er selve optællingen af bøger foretaget - er det ved tykke bøger eller ved tegneserierne? osv. Måske er der også mulighed for at spørge biblioteket om hvor mange bøger de har.
Eksempel på modellering i udskoling
Elever i 8. klasse undersøger forskellige hverdagssituationer, der foregår om morgenen, inden skolen begynder. Karla vil undersøge: “Hvor mange gange tandbørstning der er til i en almindelig tube tandpasta”.
- I oversættelse fra omverdensituationen til det matematiske domæne, overvejer Karla, hvordan hun kan måle dette. Hun noterer sig, at der står 75 ml uden på tuben. Hun laver nogle tegninger og begynder at trykke lidt af tandpastaen ud på et stykke papir. Hun tegner en cylinder og finder formlen for rumfanget af en cylinder:
($V=\pi \cdot r^2 \cdot h$). Karla beskriver sine antalgelser som at a) tandpastastriben er cylinderformet, b) at alt tanspastaen kan trykkes ud i denne form, c) at man bruger den samme længde cylinderformet tandpasta stribe hver gang man bøster tænder. - I den matematiske problemløsning går Karla i gang med at måle på tandpastastriben. Hun måler længden af striben til 1,5 cm. Hun prøver at måle først radius ved at snitte lodret ned gennem midteraksen i striben. Hun måler også diameteren af hullet i tuben og diameteren af striben i et lodret snit, som hun laver med linealen. Efter en del målinger bestemmer hun sig for, at diameteren af en normal stribe er 0,7 cm. Radius beregnes til 0,35 cm. Ved indsættelse af de målte størrelser på en lommeregner får hun: $\pi \cdot 0,35^2 \cdot 1,5 = 0,6$ Hun skriver derved at rumfanget er 0,6 cm3 og efter at have snakket lidt med en kammerat om sagen skriver hun, at 1 ml = 1 cm3 og at de 0,6 cm3=0,6 ml, og herefter beregner hun, hvor mange tandbørstninger der er til i tuben: $\frac{75ml}{0,6ml} = 125$.
- I fortolkningen af svaret bliver Karla her lidt overrasket over resultatet, da hun synes, det er lidt højt, men sammen med læreren når de frem til, at en familie på 4 kan bruge en tube på 15 dage, og dette er ok for eleven.
- I valideringen af den anvendte model udfordrer læreren eleven til i stedet at beregne, hvor lang en stribe, man kan lave af en hel tube. Eleven sætter 75 cm3 ind i formlen for rumfanget af en cylinder, isolerer h og beregner med lommeregneren h til 195 cm. Eleven går derefter i gang med at afprøve dette med en tube tandpasta. Eleven kan nu undersøge om hun kommer frem til samme resultat i de to udregninger og overveje hvorfor der muligvis er forskellige i de to resultater. Hvad kan fejlkilderne være osv.
At anvende, fortolke, diskutere og kritisere modeller
Arbejdet med at fortolke, kritisere og diskutere matematiske modeller, beskrives også nogle gange som den analyserende del af modellering. Her opstiller eleverne ikke selv modeller, men arbejder med allerede eksisterende matematiske modeller.
Denne del af arbejdet med matematisk modellering i skolen handler om, at eleverne både skal kunne analysere grundlaget og egenskaberne for forskellige modeller. Derudover skal eleverne også arbejde med at kunne bedømme modellernes rækkevidde og holdbarhed, men det handler også om at kunne afkode og fortolke fundne resultater i forhold tilsituationen fra omverdenen.
Når elever undervises i modellering, skal de derfor også arbejde med at kritisere og reflektere over anvendelsen af matematiske modeller i alle delprocesserne.
- Giver oversættelsen fra omverdensproblem til matematik mening?
- Kan det formulerede spørgsmål/problem besvares/løses vha. matematisk modellering?
- Giver fortolkningen af de matematiske svar andledning til nye spørgsmål?
- Er modellen rimelig/tilstrækkelig, hensigtsmæssig i forhold til omverdensituationen?
Det er en god ide at arbejde med situationer, som eleverne kan se betydningen eller relevansen af, og som de umiddelbart kan forholde sig til. Der tales om autentiske situationer som udgangspunkt for modellering, når situationer findes i virkeligheden, fx når eleverne undersøger deres eget mobilabonnement, og om semisituerede situationer, når eleverne undersøger en konstrueret virkelighed, fx ud fra forbrugsdata og prisblad for en fiktiv situation, hvor en person skal tage stilling til valg af mobilabonnement.
Arbejdet med modellering kan lægge op til en tværfaglig tilgang, således, at arbejdet med matematisk modellering kan spille sammen med tilegnelse af begreber og teorier inden for andre fagområder, fx i en STEM sammenhæng.
En model til indskolingen

I indskolingen kan eleverne undersøge allerede opstillede tabeller, fx temperaturtabeller se figur 2.2, hvor de skal arbejde med at afkode, analysere og fortolke disse målinger. På figur 2.2. kan der spørges til, om det er varmest i ugen i december eller ugen i januar? I dette eksempel kan eleverne starte med at forstå tabellen, hvad viser tabellen - hvad er tallene i tabellen en model af. Derudover kan det drøftes, hvordan man i hverdagen måler, hvor varmt eller koldt det er. Kan det gøres på forskellige måder - kan der være forskellige forhold, der påvirker målingen? Derudover kan der drøftes, hvordan man kan sammenligne de to tabeller. Nogle vil måske sammenligne de enkelte dage - ”mandag er det varmest i december” osv., andre vil måske lægge alle temperaturerne sammen i december og sammenligne med summen af temperaturerne i januar. Hvordan argumenterer eleverne for deres svar? Som lærer må man være opmærksom på om eleverne har brug for støtte til at holde styr på de negative temperaturen ved en evt. beregning af summen.
Der kan i klassen også laves egne modeller til at sammenligne med den opstillede tabel, eller der kan sammenlignes med andre landes temperaturmålinger. Vil man altid kunne sammenligne sådanne målinger? Hvilke forhold skal der tages hensyn til?
Undersøg modeller på mellemtrinnet
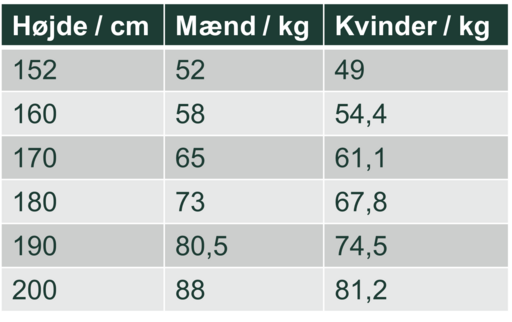
På mellemtrinnet eller i udskolingen kan eleverne fx undersøge en model for en idealvægt (Kilde 7). Eleverne kan her starte med fælles at lære modellen at kende, hvorefter eleverne kan vælge mellem forskellige analyseelementer, så man til sidst vurderer modellen sammen. Modellen her benævnes J. D. Robinson-formlen og skrives således:
Mænd: 52 kg + 0,75 kg per cm (for højden over 1,52 m)
Kvinder: 49 kg + 0,67 kg per cm (for højden over 1,52 m)
Først kan der indsættes nogle eksempler for at se, hvad outputtet bliver. Derefter kan det drøftes, hvad modellen bygger på, og hvad de forskellige variable og konstanter i modellen er. Gyldighedsområdet kan også drøftes - hvad er den mindste højde, der kan indsættes, og hvad kunne den største værdi være? Hvad bliver modellens resultatområde?
Sammenhænge i modellen kan nu undersøges. Hvilken sammenhæng er der mellem højden og vægten for mænd og for kvinder? (evt. kan der snakkes begyndende funktioner her). Der kan laves en tabel for sammenhængen og evt. en graf for sammenhængen (se figur 2.3).
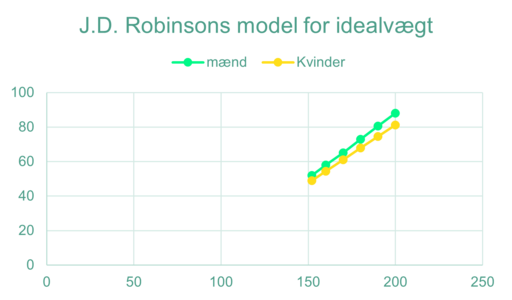
Til sidst kan det drøftes, om der er behov for ændringer af modellen. Hvad vil det fx betyde, hvis man ændrede nogle af konstanterne. Hvordan vil tabellen/grafen så se ud? Der kan også sammenlignes med den klassiske model for BMI (body Mass Index), hvor der udregnes et indekstal, der beregnes ud fra personens vægt og højde. BMI = vægt(kg) / højde(m)2.
Hvilke variable og konstanter er der i denne model, og hvad er sammenhængen mellem de to modeller? Ligger Robinsons værdierne alle inden for BMI-definitionen af et interval, der indikerer normal vægt. Sluttelig kan det drøftes, hvad man overhovedet kan bruge sådanne modeller til, og hvad man specielt skal være opmærksom på. Hvad er der fx ikke er taget hensyn til?
Eksemplet med idealvægt kan være følsomt for elever, der har det vanskeligt med deres egen vægt. Det er derfor vigtigt ikke at udstille eleverne og man skal ikke bruge data om eleverne. Samtidigt er det en vigtig pointe, at matematiske modeller som fx normalvægt har en stor indflydelse på, hvad vi anser som normalt, og dermed på hvordan vi opfatter os selv. Disse formaterende og normative aspekter af matematiske modeller er vigtige, og bør gøres til genstand for refleksion og kritik. Derfor er aktiviteten relevant.
Ulighed og Gini koefficient i udskolingen
Elever i udskolingen kan fx diskutere, hvordan man modellerer ulighed, og hvilke problemer der kan være forbundet med at forsøge at måle dette fænomen. I denne forbindelse giver det mening at undersøge Gini-koefficienten.
Gini-koefficienten er en model for uligheden i et samfund. Koefficienten beregnes ved at se på indkomstfordelingen (fx opdelt i deciler) for et land eller en region. I en hypotetisk fuldstændig lige indkomstfordeling vil 10 % af befolkningen tegne sig for nøjagtig 10 % af den samlede indkomst, 20 % af befolkningen for 20 % af den samlede indkomst og så fremdeles. I Danmark (i 2018) havde de 10 % fattigste tilsammen ca. 3 % af landets samlede disponible indkomst, hvorimod de 10 % rigeste sad på 23%. Dette kan stilles op i et skema som figur 2.4.
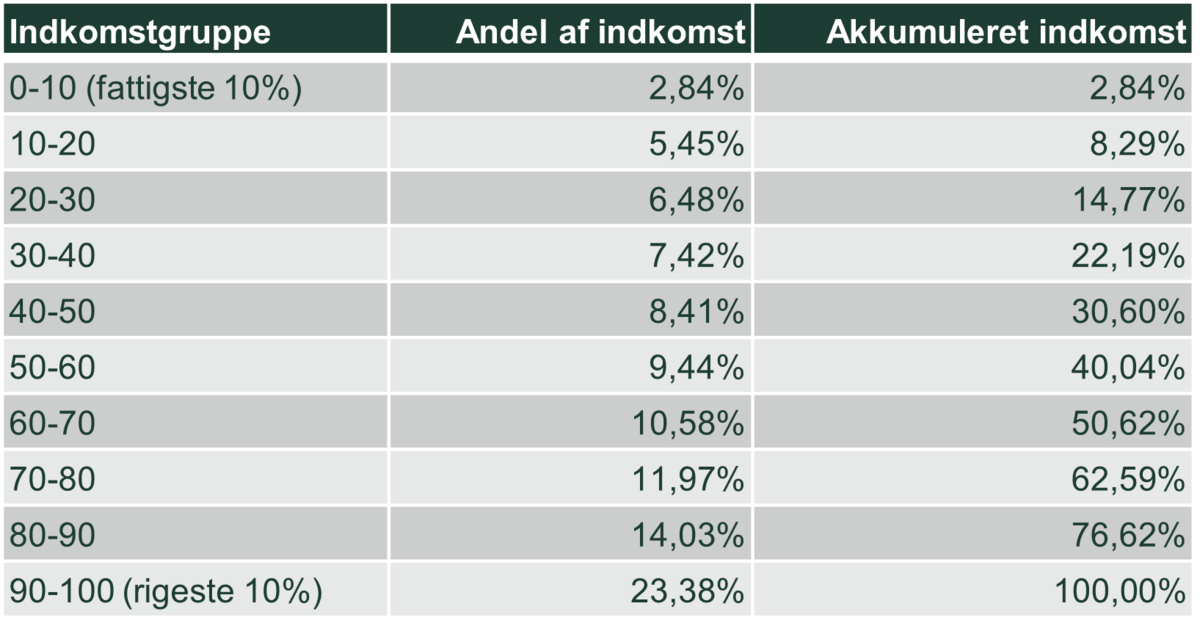
Ved at plotte indkomst som funktion af andelen af befolkningen ordnet efter indkomst opnås Lorenz kurven, og arealet under Lorenz kurven er et udtryk for uligheden i samfundet (se figur 2.5). Gini koefficienten beregnes som forholdet mellem arealet under Lorenz kurven og arealet under en kurve der repræsenterer en helt lige indkomstfordeling (dette vil være en ret linje med hældning 1.)
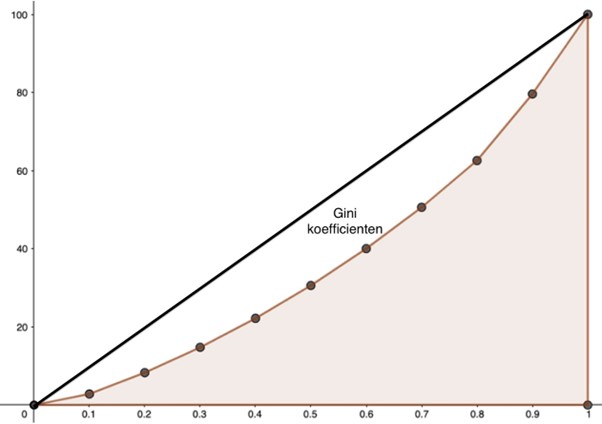
Eleverne kan arbejde med Lorenz kurven og Gini koefficienten på mange måder:
Hvordan ser Lorenz-kurven ud for Danmark? For USA og for hele verden? Hvad betyder det for verdens befolkning, at grafen ser ud, som den gør? Hvordan mener eleverne, at grafen helst skal se ud? Er det realistisk - hvorfor/hvorfor ikke? Hvilken betydning ville det have for Lorenz-kurve (og Gini-koefficient), hvis alle danskere tjente 5000 kr. mere pr måned? Eller hvis alle i stedet fik en lønstigning på 10%?
Spørgsmål til fagteamet
- Hvilke erfaringer har I med at arbejde med aktiv modellering i jeres klasse? Giv gerne eksempler på elevernes arbejde i de forskellige delprocesser i modelleringscyklussen.
- Har I erfaringer med at arbejde med at være kritisk overfor forskellige matematiske modeller? Giv gerne eksempler på de modeller, I har diskuteret og drøftet i klassen. Hvorfor valgte I netop at arbejde med disse modeller?
- Har I eksempler, hvor oversættelsen fra en oplevet virkelighed til matematik, er enten svær at forstå eller let at få til at give mening? Hvad adskiller disse eksempler?
til: GRUNDSKOLE
emne: MODELLERING
UDGIVET: 2023
Forfatter
Dorte Moeskær Larsen
Lektor, ph.d.
UCL Erhvervsakademi og Professionshøjskole
Morten Misfeldt
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Blomhøj, M. (2006). Mod en didaktisk teori for matematisk modellering. I O. Skovsmose og M. Blomhøj (red.) Kunne det tænkes? – om matematiklæring, København: Malling Beck, 80-109.
- OECD (2013). PISA 2015 draft mathematics framework. Paris, France: OECD Publishing.
- Poulsen, E. T. (2001). Matematikken og virkeligheden. I M. Niss (Red.), Matematikken og Verden (s. 19–36). København: Fremad.
- Doerr, H. M., Ärlebäck, J. B., & Misfeldt, M. (2017). Representations of modelling in mathematics education. In: Mathematical modelling and applications (s. 71-81). Springer, Cham.
- Fink, K. Blankholm, T. & Skånstrøm, Mikael (2020) Matematiske kompetencer i praksis. Forlaget matematik.
- Undervisningsforløb om matematiske modeller fra KiDM projeketet. http://kidm.dk/matematik/laerer/matematik-laerer/oversigt/de-tre-indsatser/indsats-1/hvor-mange-boeger-paa-biblioteket/
- Pind, P. & Bjerre, E. (2019). Modellering og Estimering i matematikundervisningen. Forlaget Pind og Bjerre.
- Blomhøj, M. og Skånstrøm, M. (2006): Matematikmorgener. I: Skovsmose, O. og Blomhøj, M. (red.), Kunne det tænkes? – om matematiklæring, (s. 7-23). København: Forlag Malling Beck.
- Niss, M. & Jensen, T. H. (2002). Kompetencer og matematiklæring – ideer og inspiration til udvikling af matematikundervisning i Danmark. Uddannelsesstyrelsens temahæfteserie nr. 18. København: Undervisningsministeriet.