Matematikhistoriske eksempler
Eksempel I: Ligningernes historie
Helt tilbage til de tidligste skriftlige kilder, vi har i matematikkens historie, er der fundet tekster med opgaver, hvis løsning svarer til, hvad vi i dag ville kalde løsning af ligninger. I den ægyptiske tekst kaldet Papyrus Rhind, kopieret af Ahmes ca. 1650 fvt, er der en række praktiske opgaver som f.eks. beregning af skatter og løn, der svarer til at løse 1. gradsligninger. Babyloniske lertavler fra 2000-1700 fvt indeholder mange eksempler på såkaldte ”grøftegravningsopgaver”, der svarer til at løse, hvad vi i dag kalder for 2. gradsligninger. Opgaverne er f.eks. af typen, hvor man kender summen af sidernes længder og arealet af en rektangulær grøft, og man skal finde længden af siderne. Løsningerne er skrevet op på lertavler, der i ord beskriver, hvad man skal gøre for at finde de to tal.
I antikken i det gamle Grækenland er de mest kendt for at have arbejdet med geometri og talteori, men der er et værk fra ca. 250 evt., der handler om løsning af ligninger. Det er skrevet af matematikeren Diophant fra Alexandria. I hans arbejder er der begyndende algebraisk notation, men ellers minder det om, hvad der er fundet i babyloniske og ægyptiske tekster.
Efter profeten Muhammed erobrede Mekka i 630 bredte det islamiske rige sig, og med kaliffen al-Mansurs grundlæggelse af Bagdad i 760’erne opstod der her et centrum for kommerciel og videnskabelig udvikling. Kaliffen Hārūn al-Rashīd oprettede et bibliotek, og der blev indsamlet og oversat græske og indiske manuskripter til arabisk. Hans efterfølger, kaliffen al-Ma’mūn (786-833), etablerede videnskabsakademiet Visdommens Hus, hvor matematikeren Muhammed ibn Mūsā al-Khwārizmī holdt til omkring 825. Fra hans arbejder er der to værker, som er overleveret, et om løsning af ligninger og et om aritmetik.
I dette eksempel præsenterer vi korte uddrag af al-Khwārizmīs bog om løsning af ligninger, hvor han bl.a. præsenterede en systematisk gennemgang af løsninger af alle typer af 2. gradsligninger (med positive koefficienter). Bogen har titlen Al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr waʾl-muqābala, som betyder noget i retning af lærebog om regning ved fuldstændiggørelse (al-jabr) og sammenligning (al-muqābala). Ordet ’algebra’, der i dag bl.a. dækker over matematiske teorier for ligningsløsning, stammer fra al-Khwārizmīs al-jabr, som referer til at flytte en størrelse, der trækkes fra på den ene side af ligningen, til den anden side, hvor den så bliver en størrelse, der lægges til. Al-muqabala referer til at reducere en positiv størrelse ved at trække det samme fra på begge sider af ligningen. Det er ikke kun al-Khwārizmīs titel på bogen, vi kan finde i vor tids sprogbrug, også al-Khwārizmīs navn lever videre i dag i ordet ’algoritme’.
I det følgende vil vi introducere al-Khwārizmīs bog og præsentere uddrag, som illustrerer hans systematiske tilgang, og give et eksempel på, hvordan han argumenterede for sin beregningsmetode. Vi slutter af med at give forslag til, hvordan emnet kan bruges i gymnasiets matematikundervisning til at illustrere:
- at der i forskellige kulturer gennem tiderne har levet mennesker, der har beskæftiget sig med og udviklet matematik
- betydningen af systematik, abstraktion og symbolsprog i matematik.
Kildeteksterne og den historiske udvikling vil ikke blive gennemgået som sådan, i stedet henvises til Andersens bog om ligningernes historie (Kilde 1). I forhold til babylonsk ligningsløsning henvises til Høyrups bog Algebra på Lertavler for gymnasiet (Kilde 10) og for ægyptisk matematik til Frandsens gymnasiebog Ægyptisk matematik (Kilde 7).
Al-Khwārizmīs løsning af 2. grads ligninger (kildetekst 1 og kildetekst 2)
Kildetekst 1 er en dansk oversættelse af uddrag af al-Khwārizmīs bog om løsning af ligninger. Han indledte sin bog med at forklare, at han har begrænset sig til, ”hvad der er nyttigst i regning”, som folk havde brug for i forbindelse med bl.a. sager som f.eks. arv, handel og landopmåling. Han forklarede, at der er tre slags tal, der er brug for, når man regner med fuldstændiggørelse (al-jabr) og sammenligning (al-muqābala), nemlig rødder, kvadrater og tal. Ved en rod forstod han en størrelse, som ganges med sig selv, og et kvadrat er roden ganget med sig selv. Al-Khwārizmī skrev alting ud i ord, men hvis vi indfører moderne notation, kan vi kalde en rod for $x$, og kvadrattet kan så betegnes med $x^2$.
Kildetekst 1 og kildetekst 2 er primært uddrag fra den del af bogen, der handler om 2. gradsligninger. Der er kun positive koefficienter, så al-Khwārizmīs systematiske undersøgelse af 2. gradsligninger gav anledning til 6 typer. I slutningen af 3. afsnit af kildetekst 1 kan man se, at han først opremsede de tre typer, som han kaldte ”kvadrater lig med rødder” ($ax^2 =bx$), ”kvadrater lig med tal” ($ax^2=c$) og ”rødder lig med tal” ($ax=c$). Efter at have givet eksempler på, hvordan disse typer løses, fortsatte han med at opskrive de resterende tre blandede typer, som han kaldte dem: ”kvadrater og rødder lig med tal” ($ax^2 + bx = c$), ”kvadrater og tal lig med rødder” ($ax^2 + c =bx$) og ”rødder og tal lig med kvadrater” ($bx + c = ax^2$). Al-Khwārizmī gennemgik metoderne til at løse 2. gradsligningerne ved eksempler. Hans løsningseksempel på ligninger af typen ”rødder og kvadrater lig med tal” er gengivet i det sidste afsnit i kildetekst 1, hvor han viser, hvordan man finder (den positive) løsning til ligningen $x^2 + 10x =39$.
Kildetekst 1
AL-KHWĀRIZMĪ
al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr w’al-muqābala
I den nådige og barmhjertige Guds navn!
Dette arbejde blev skrevet af Mohammed Ben Musa fra Khowarezm.
[...]
Den kærlighed til videnskaben, med hvilken Gud har udmærket imanen Al Mamun, de troendes hærfører (ved siden af det kalifat, som han har fundet ham værdig til ved lovlig succession, hvis dragt han har iført ham, og hvis æresbevisninger han har udsmykket ham med), den venlighed og imødekommenhed, som han viser de lærde, den beredvillighed med hvilken han beskytter og understøtter dem i opklaringen af dunkelheder og i fjernelsen af vanskeligheder, har opmuntret mig til at forfatte et kort arbejde om beregning ved hjælp af fuldstændiggørelse og sammenligning, hvor jeg har begrænset det til, hvad der er lettest og nyttigst i regning, sådan noget som folk hele tiden har brug for i tilfælde af arv, opdeling, retssager og handel og i alle deres indbyrdes forretninger, eller hvad der angår landopmåling, kanalgravning, geometrisk beregning og andre forskellige slags ting.
[...]
Da jeg overvejede hvad folk i almindelighed behøver, når de regner, fandt jeg, at det altid er et tal.
Jeg bemærkede også, at ethvert tal er sammensat af enheder og at ethvert tal kan opdeles i enheder.
Endvidere fandt jeg, at ethvert tal mellem en og ti overgår det foregående med én enhed; derefter fordobles eller tredobles ti nøjagtigt som enhederne før blev det. Således opstår tyve, tredive, osv. indtil hundrede; så fordobles og tredobles på samme måde som med enhederne og tierne, op til tusind; så kan man gentage tusind på samme måde op til et hvilket som helst indviklet tal; og så fremdeles til det tælleliges yderste grænse.
Jeg bemærkede, at der er tre slags tal, der kræves, når man beregner ved fuldstændiggørelse og sammenligning, nemlig rødder, kvadrater og simple tal, der ikke har med hverken rod eller kvadrat at gøre.
En rod er en størrelse som ganges med sig selv, bestående af enheder, og det være sig hvad der er herover af tal og hvad der er herunder af brøkdele.
Et kvadrat er hele rodens størrelse ganget med sig selv.
Et simpelt tal er et tal som kan udtrykkes uden henvisning til rod eller kvadrat.
Et tal der hører til en af disse klasser kan være lig med et tal fra en anden klasse, man kan f.eks. sige “kvadrater lig med rødder” eller “kvadrater lig med tal” eller “rødder lig med tal”.
[...]
Jeg fandt at disse tre slags, nemlig rødder, kvadrater og tal, kan kombineres, og således fremkommer der tre blandede typer: “kvadrater og rødder lig med tal”, “kvadrater og tal lig med rødder” og “rødder og tal lig med kvadrater”.
Rødder og kvadrater lig med tal: For eksempel “et kvadrat og ti rødder af samme beløber sig til niogtredive dirhem (møntenhed)”; dermed menes, hvad er det kvadrat der efter at være blevet forøget med ti af sine egne rødder beløber sig til niogtredive? Løsningen er denne: man halverer antallet af rødder, hvad der i dette tilfælde giver fem. Dette tal ganger man med sig selv; produktet er femogtyve. Læg niogtredive til; summen er fireogtres. Uddrag nu roden heraf, som er otte, og træk fra denne halvdelen af antallet af rødder, som er fem; resten er tre. Dette er roden af det kvadrat man søger; kvadratet selv er ni.
-Kildetekst 1 Uddrag fra K. Andersen, red. (1986). Kilder og kommentarer til Ligningernes historie. Vejle: Forlaget Trip, s. 92-94. Dansk oversættelse af uddrag af (al-Khwarizmi, 1831).
I eksemplet, der er gengivet i kildetekst 2, illustrerede al-Khwārizmī, at han udemærkede var klar over, at 2. gradsligninger af typen ”kvadrater og tal lig med rødder” kunne have to, en eller ingen (positive) rødder. Han viste metoden med eksemplet $x^2 + 21 = 10x$. Dette er endnu et eksempel på al-Khwārizmīs systematik i undersøgelsen af løsninger til 2. gradsligninger.
Kildetekst 2
Kvadrater og tal lig med rødder: For eksempel "et kvadrat og enogtyve i tal er lig med ti rødder af det samme kvadrat". Det vil sige, hvad må et kvadrat beløbe sig til, som, når enogtyve dirhem lægges til det, bliver lig med hvad der svarer til ti rødder af dette kvadrat? Løsning: Halvér antallet af rødder; halvdelen er fem. Gang dette med sig selv; produktet er femogtyve. Træk fra dette de enogtyve som er forbundet med kvadratet; resten er fire. Uddrag roden; den er to. Træk dette fra halvdelen af rødderne, som er fem; resten er tre. Dette er roden af det kvadrat som blev krævet, og kvadratet er ni. Eller man kan lægge roden til halvdelen af rødderne; summen er syv; dette er roden af det kvadrat som blev søgt og kvadratet selv er niogfyrre.
Når man træffer på et eksempel som henivser en til dette tilfælde, skal man forsøge at løse det ved addition, og hvis det ikke går, så går det helt sikkert med subtraktion. For i dette tilfælde kan man anvende både addition og subtraktion, hvad man ikke kan i noget andet af de tre tilfælde i hvilke antallet af rødder må halveres. Og man skal vide, at når man i et spørgsmål der hører ind under dette tilfælde har halveret antallet af rødder og ganget halvdelen med sig selv og fået et produkt, der er mindre end antallet af dirhem forbundet med kvadratet, så er eksemplet umuligt; men hvis produktet er lig med antallet af dirhem i sig selv, så er roden af kvadratet lig med halvdelen af rødderne alene, uden hverken addition eller subtraktion.
I hvert tilfælde, hvor man har to kvadrater eller mere eller mindre, skal man reducere dem til ét helt kvadrat, sådan som jeg forklarede undet det første tilfælde.
- Kildetekst 2 Uddrag fra K. Andersen, red. (1986). Kilder og kommentarer til Ligningernes historie. Vejle: Forlaget Trip, s. 95. Dansk oversættelse af uddrag af (al-Khwarizmi, 1831).
Al-Khwārizmīs geometriske bevis (kildetekst 3)
Al-Khwārizmīs stil minder om babyloniernes, idet han giver en algoritme til, hvordan man finder rødderne (og kvadraterne), men han udførte en systematisk og generel undersøgelse. Et andet punkt, hvor al-Khwārizmīs bog adskiller sig fra, hvad vi ser på de babyloniske lertavler, er, at al-Khwarizmi i sin tekst redegjorde for, at det er nødvendigt at give et geometrisk bevis for, at metoderne er korrekte. I kildetekst 3 ses et eksempel på et sådan bevis med udgangspunkt i ligningen $x^2 + 10x = 39$.
Kildetekst 3
Vi har sagt nok, for så vidt vi taler om tal, omkring de 6 typer af ligninger, siger Al-Khowaizimi. Nu er det imellemtiden nødvendigt at vi geometrisk demonstrerer sandheden af de samme problemer som vi netop har forklaret ved hjælp af tal. Derfor er vores første proposition denne, at et kvadrat og 10 rødder er lig med 39 enheder.
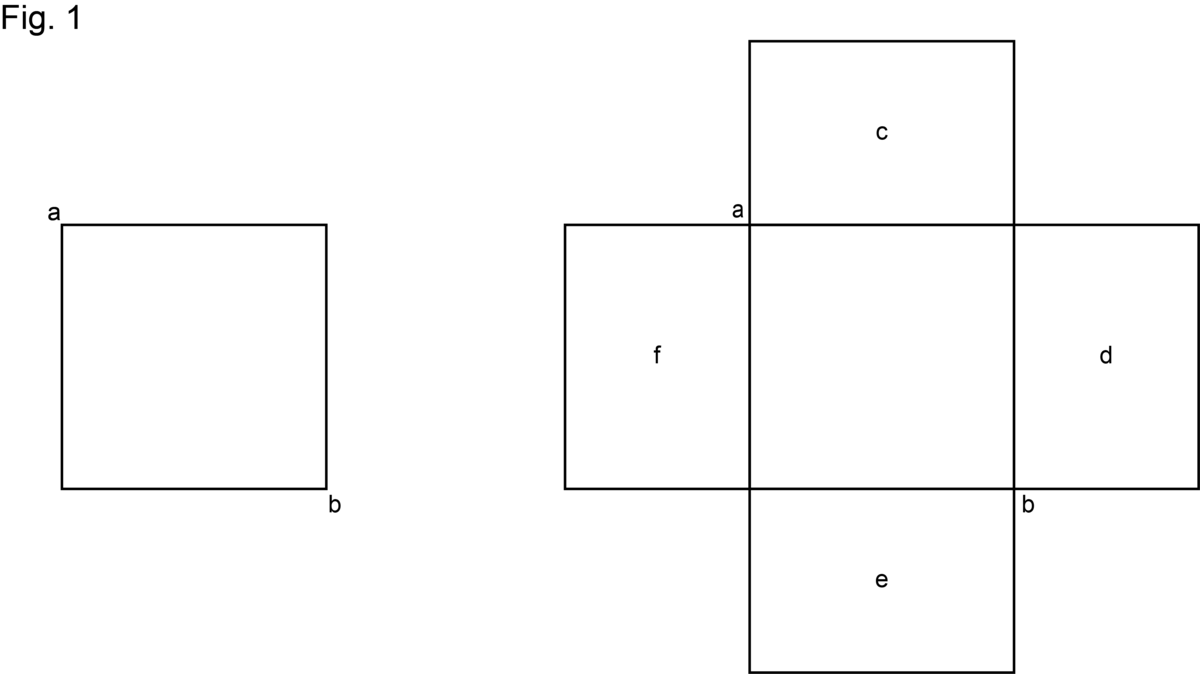
Beviset er at vi konstruerer (Fig. 1) et kvadrat med ukendte sidelænger, og lader dette tegnede kvadrat repræsentere kvadratet (anden potens af den ukendte) som du sammen med dets rødder ønsker at finde. Lad da kvadratet være $ab$, hver af siderne repræsenterer så en rod. Når vi multiplicerer en hvilken som helst side af dette med et (eller flere) tal, er det indlysende, at det, der fremkommer ved multiplikationen, vil være et antal rødder svarende til roden af det samme tal (af kvadratet). Da vi har ti rødder sammen med kvadratet, tager vi en fjerdedel af tallet ti og påfører hver side af kvadratet et område med lige lange sider, hvis længde skal være den samme som længden af det først beskrevne kvadrat, og hvis bredde er 2½, hvilket er en fjerdedel af 10. Derfor påføres der på det første kvadrat, $ab$, fire områder med lige store sider. Hver af disse har en længde, der svarer til længden af én rod af kvadratet $ab$, og hver bredde er også 2½, som vi netop har sagt. Disse områder er nu $c$, $d$, $e$, $f$.
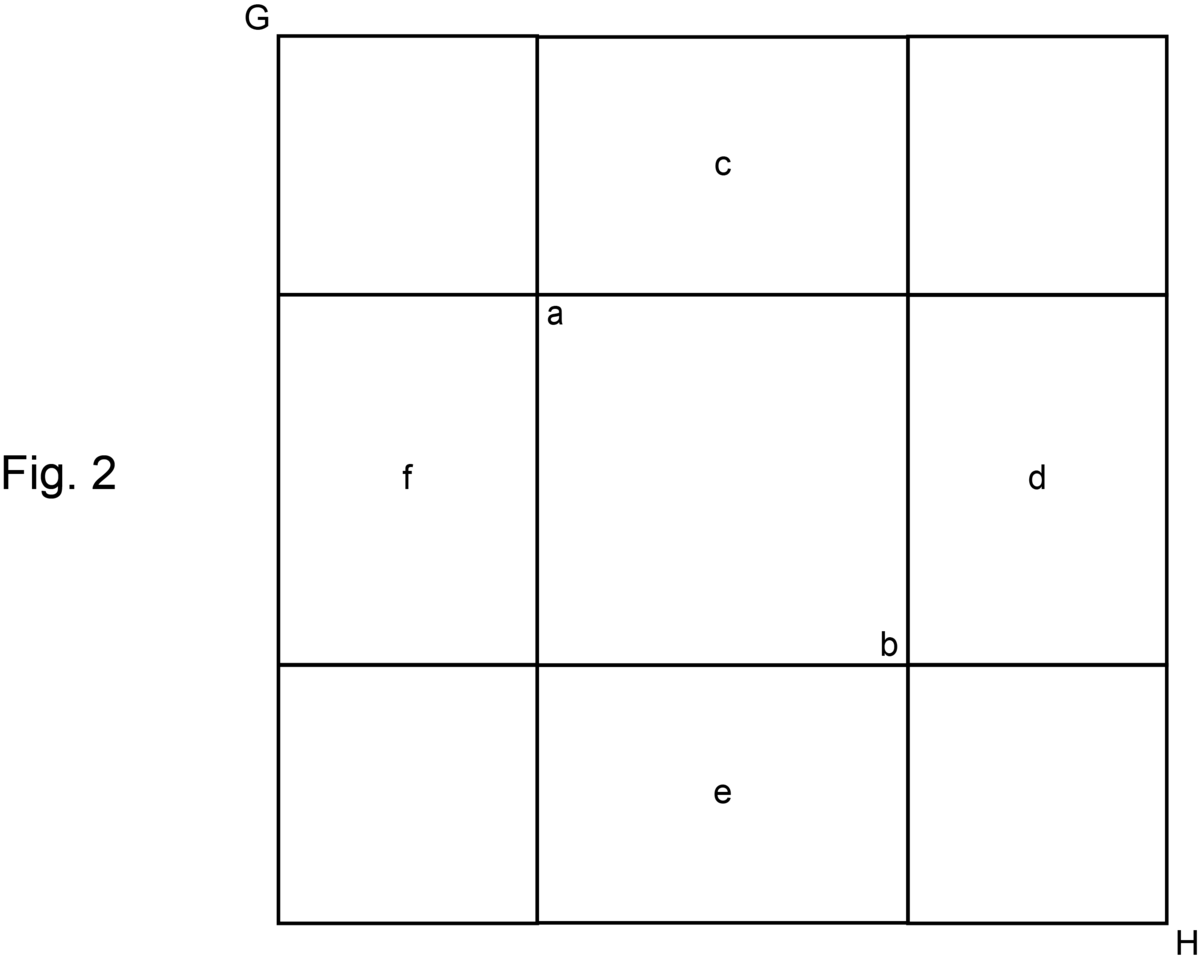
Denne tre'er udtrykker således én rod af det tegnede kvadrat, det vil sige én rod af det givne kvadrat af den ukendte, og 9 udgør selve kvadratet. Derfor tager vi halvdelen af ti og multiplicerer dette med sig selv. Vi lægger derefter hele produktet af denne multiplikation til 39, så tegningen af det større kvadrat $GH$ kan fuldendes; for manglen på de fire hjørner gjorde tegningen af hele dette kvadrat ufuldstændig. Nu er det indlysende, at en fjerdedel af et hvilket som helst tal multipliceret med sig selv og derefter ganget med fire, giver det samme resultat som halvdelen af tallet multipliceret med sig selv. Derfor, hvis halvdelen af roden multipliceres med sig selv, vil summen af denne multiplikation udligne, svare til eller ophæve multiplikationen af fjerdedelen med sig selv og derefter med fire.
-Kildetekst 3 Uddrag af al-Khwārizmīs bog om ligninger Al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr waʾl-muqābala. citeret fra D. Struik (ed.) A Source Book in Mathematics, 1200-1800. Cambridge, Massachussetts: Harvard Unversity Press, s. 58-60. Engelsk oversættelse af en latinsk oversættelse af Robert af Chester fra ca. 1140. Dansk oversættelse ved Clemens Merker.
Al-Khwārizmīs geometriske bevis minder om det, Jens Høyrup (Kilde 10) har kaldt for et ”klippe-klistre” argument, som kan udledes fra babyloniernes beskrivelse af, hvad man skal gøre for at finde de ubekendte i grøftegravningsopgaver. Men i modsætning til babylonierne angav al-Khwārizmī eksplicit, som han skrev i begyndelsen af uddraget i kildetekst 3, at det er nødvendigt geometrisk at bevise ”sandheden af de problemer, vi har forklaret med tal”, hvilket er mere i stil med den græske tradition. Græsk og indisk matematik blev kendt i den arabiske verden i middelalderen gennem oversættelser af skriftlige værker, mens vi ikke ved så meget om indflydelsen fra Mesopotamien. Her er der teorier om, at der har eksisteret en gådetradition. Teorien er baseret på, at der dukker opgaver op i senere kulturers skrifter, der minder om opgaver, der findes på babyloniske lertavler (se kilde 10).
Der blev også arbejdet med 3. gradsligninger i det islamiske rige i middelalderen. Her er Umar ibn Ibrāhīm al-Khayyāmī (1048-1131) kendt for sin systematiske klassifikation af 3. gradsligninger og løsninger af disse ved skæring af keglesnit. De første algebraiske løsningsformler til 3. gradsligninger blev udviklet i 1500 tallet af italienske matematikere.
I undervisningen kan man lade sig inspirere af refleksionsspørgsmål som dem, der er angivet i Lützen og Ramskovs (Kilde 17, s.36) bog Kilder til matematikkens historie til bl.a. ovenstående tekstuddrag fra al-Khwārizmīs bog. En læsning af al-Khwārizmīs tekst med henblik på at ”afkode” en løsningsalgoritme til 2. gradsligninger sammenholdt med al-Khwārizmīs geometriske bevis, kan styrke elevernes forståelse af formlen for løsning af 2. gradsligning, som de kender fra deres formelsamling. En diskussion af al-Khwārizmīs klassificering af 2. gradsligninger i 6 typer og hans tilhørende løsningseksempler, har potentiale til at påvirke elevernes begrebsbillede af 2. gradsligninger (se kilde 8 i 'Teoretiske konstruktioner') samt illustrere betydningen af systematik, abstraktion og symbolsprog i matematik.
Al-Khwārizmīs geometriske bevis kan sammenholdes med et algebraisk bevis, der ofte gives i nutidige lærebøger. Det kan give anledning til en diskussion af, hvad der tæller som et gyldigt bevis, hvorfor matematikere insisterer på beviser, og hvilken rolle beviser har spillet i matematikkens historieske udvikling. I forhold til de didaktiske teorier i 'Teoretiske konstruktioner', kan sådanne diskussioner give anledning til at illustrere for eleverne, at der er meta-diskursive regler i matematik, og at disse har ændret sig over tid.
Endelig kan man i undervisningen inddrage tekster fra Høyrups (Kilde 10) bog om grøftegravningsopgaver fra babyloniske lertavler og sammenligne disse tekster med Al-Khwārizmīs behandling af 2. gradsligninger. En sådan sammenlignende analyse kan øge elevernes historiebevidsthed i forhold til matematik, som noget der har været dyrket, udviklet og udvekslet af og mellem mennesker i diverse kulturer gennem tiden.
Eksempel II: Infinitesimalregningens historie
Det vi i dag kalder for differential- og integralregning blev udviklet hver for sig. Differentialregning blev udviklet som metoder til at finde ekstremumspunkter og tangenter for kurver, mens integralregning blev udviklet som metoder til bestemmelse af arealer og rumfang. I 1600-tallet blev de to problemfelter forenet på forskellig vis med Isaac Newtons (1642-1727) og Gottfried Wilhelm Leibnizs (1646-1716) arbejder. Newton og Leibniz indså uafhængigt af hinanden sammenhængen mellem de to typer af problemer, og de arbejdede begge på at finde generelle løsningsmetoder og algoritmer. Newton og Leibniz bliver derfor i litteraturen ofte omtalt som dem, der skabte differential- og integralregningen.
I dag er funktioner det essentielle matematiske objekt i differential- og integralregning, som bygger på grænseværdibegrebet og baserer sig på de reelle tal. Funktionsbegrebet blev imidlertid først indført i matematikken i 1700-tallet af Leonard Euler (1707-1783), så differential- og integralregningen blev udviklet forud for indførelsen af funktionsbegrebet, som i vores nutidige forståelse er det, differential- og integralregning handler om.
Det moderne grænseværdibegreb tilskrives som oftest Bernard Bolzanos (1781-1848) og Augustin-Louis Cauchys (1789-1857) arbejder. Og det vi i dag kender som epsilon-delta formaliseringen af grænseværdibegrebet skyldes Karl Weierstrass’s (1815-1897) arbejde. De reelle tal blev indført i slutningen af 1800-tallet med Weierstrass, Georg Cantor (1845-1918), Richard Dedekind (1831-1916) og Eduard Heine (1821-1881) som hovedpersoner.
Dette korte rids viser, som det ofte er tilfældet med forskning og formidling af matematik, at matematik som regel formidles i artikler og lærebøger i en anden rækkefølge end den, der beskriver tilblivelsen. Det er der mange gode grunde til, som vi ikke vil komme nærmere ind på her, men en af bagsiderne er, at den matematiske skabelsesproces usynliggøres. Med matematikkens historie som særskilt emne i pensum i skolematematikken kan der dog rådes bod på det om ikke før så i hvert fald i gymnasiets matematikundervisning.
I det følgende vil vi præsentere korte uddrag af kildetekster fra Pierre de Fermats (1601-1665), Newtons og Guillaume de l’Hôpitals (1661-1704) (Leibnizs metode) arbejder og diskutere, hvordan de kan bruges i gymnasiets matematikundervisning til at tjene to formål:
-
synliggøre skabelsen af matematik for eleverne og derved udvikle deres historiebevidsthed i forhold til matematik.
-
understøtte elevernes matematiklæring på forskellig vis, især i forhold til de udfordringer, der belyses i de didaktiske teorier introduceret i 'Teoretiske konstruktioner'.
Kildeteksterne og den historiske udvikling vil ikke blive gennemgået som sådan, i stedet henvises til Kjeldsens kapitel om differentialregningens historie i gymnasielærebogssystemet Teori og Redskab (Kilde 12)
Fermats min-max metode (kildetekst 4 og kildetekst 5) samt forslag til brug i undervisningen
Kildetekst 4 er en oversættelse af Fermats metode til at finde maxima og minima. I dag er standardmetoden at formulere problemstillingen i termer af en differentiabel funktion af en uafhængig variabel $x$, differentiere funktionen for at finde den afledede funktion som sættes lig med $0$. Den fremkomne ligning løses for $x$ for at finde ekstremumspunkter.
Fermat præsenterede sin ”regel” som beskrevet i afsnit 2 i kildetekst 4, og derefter illustrerede han den på et eksempel, hvis løsning var velkendt, for at vise, at metoden gav det rigtige resultat. I litteraturen er det især hans erstatning af den ubekendte $a$ med $a+e$ samt det, Fermat i teksten kalder for adégaler, der i praksis betyder, at han opererede med udtrykkene på hver side som værende lig med hinanden, der er blevet diskuteret se f.eks. Pedersen (Kilde 18).
Kildetekst 4
(1) OM EN METODE TIL BESTEMMELSE AF MAKSIMA OG MINIMA
Hele teorien for bestemmelse af maksima og minima forudsætter to ubekendte størrelser og følgende regel:
Lad $a$ være en ubekendt størrelse i et givet problem (som kan være i én, to eller tre dimensioner, afhængigt af problemets formulering). Lad os angive maksimum eller minimum ved $a$ i udtryk, der kan være af vilkårlig grad. Vi erstatter nu den oprindelige ubekendte $a$ med $a + e$ og udtrykker derved den maksimale eller minimale størrelse i termer af $a$ og $e$, hvor $e$ kan optræde i vilkårlig potens. Vi vil tilpasse (adégaler), for at bruge Diophantos’ udtryk, de to udtryk for den maksimale eller minimale størrelse og eliminere deres fælles led.
Det viser sig nu, at begge sider vil indeholde led med $e$ eller potenser af $e$. Vi dividerer alle led med $e$, eller med en højere potens af $e$, således at $e$ fjernes fuldstændigt fra mindst ét af leddene. Vi undertrykker derefter alle led, hvori $e$ eller en af dets potenser stadig optræder, og vi sætter de resterende led lig hinanden; eller, hvis et af udtrykkene forsvinder, ligestiller vi de positive og negative led, hvilket er det samme. Løsningen af denne sidste ligning giver værdien af $a$, hvilket fører til maksimum eller minimum, når vi indsætter det tilbage i det oprindelige udtryk.
Her er et eksempel
At opdele linjestykket $AC$ (se Figur 1) ved $E$ således at $AE \times EC$ maksimeres.

Vi sætter $AC = b$; lad $a$ være den ene del af linjestykket, så den anden del bliver $b - a$, og produktet, hvis maksimum vi søger, er $ba - a^2$. Lad nu $a + e$ være den første del af $b$; den anden bliver da $b - a - e$, og produktet bliver $ba - a^2 + be - 2ae - e^2$. Dette skal tilpasses til det tidligere udtryk: $ba - a^2$. Ved at eliminere fælles led får vi: $be \sim 2ae + e^2$. Ved at undertrykke $e$ får vi $b = 2a$. For at løse problemet skal vi således tage halvdelen af $b$.
Vi kan næppe forvente en mere generel metode.
-Kildetekst 4 Fermats min-max metode. Fra D. J. Struik (1969). A Source Book in Mathematics. 1200–1800. Cambridge (Mass.): Harvard University Press, s. 222–225. Dansk oversættelse ved Clemens Merker.
Fermat blev afkrævet en forklaring på, hvorfor metoden virker. Til det gav han bl.a. en anden gennemgang af det samme eksempel, se kildetekst 5, hvor man kan se, hvordan Fermat har tænkt. I kildetekst 5 gør Fermat opmærksom på, at med hans metode, så undgår man problemstillingerne omkring grænseprocesser. En oplagt brug af Fermats tekster i undervisningen kunne være at sætte fokus på det, vi i dag ville kalde stringens. Ville vi f.eks. i dag mene, at Fermat har løst min/max-problemstillinger rent algebraisk uden at have brug for grænseværdiprocesser? En (lærerstyret med refleksionsspørgsmål i stil med Kilde 17) læsning af Fermats tekster kan give eleverne et indblik i Fermats forskningsproces. Fermat nævner bl.a. den franske matematiker François Viète’s (1540-1603) metoder, så man kan også have et andet fokus på læsning af kilderne, hvor man kigger efter hvilke andre og evt. tidligere matematikere, Fermat var inspireret af. Det kan lede til en diskussion af, hvordan matematik blev kendt og distribueret på Fermats tid. Kildeteksterne kan således fungere som ”vindue” ind til forskellige historiske indsigter omkring matematikkens udvikling, alt efter hvad vi ”spørger kilden om”, og hvad kilden giver os mulighed for at spørge om. I den forstand kan man arbejde med matematikhistoriske kilder på samme måde, som man i historiefaget arbejder med det funktionelle kildebegreb (se kilde 1 i Teoretiske konstruktioner).
Kildetekst 5
Ved at studere metoden for synkriseos og anastrofe af Viète og nøje følge dens anvendelse på studiet af korrelative ligninger, kom jeg på den idé at udlede en proces til at finde maksima og minima og dermed let løse alle de vanskeligheder vedrørende grænsebetingelser, som har forårsaget så mange problemer for antikke og moderne geometere.
Maksima og minima er i virkeligheden unikke og singulære, som Pappus sagde, og som de gamle grækere allerede vidste, selvom Commandino hævdede ikke at kende betydningen af udtrykket 'singulær' i Pappus. Det følger heraf, at man på den ene og den anden side af det punkt, der udgør grænsen, kan tage en tvetydig ligning, og at de to tvetydige ligninger, der opnås på denne måde, følgelig er korrelative, lige og ens.
For eksempel, lad os foreslå at opdele linjen $b$ på en sådan måde, at produktet af segmenterne bliver maksimalt. Punktet, der besvarer dette spørgsmål, er tydeligvis midtpunktet af den givne linje, og det maksimale produkt er lig $\frac{b^2}{4}$; ingen anden opdeling af denne linje giver et produkt lig $\frac{b^2}{4}$.
Men hvis man foreslår at opdele den samme linje $b$ på en sådan måde, at produktet af segmenterne bliver lig $z''$ (dette areal forudsættes desuden at være mindre end $\frac{b^2}{4}$), vil der være to punkter, der besvarer spørgsmålet, og de vil være placeret på hver sin side af punktet, der svarer til det maksimale produkt.
Lad da $a$ være et af segmenterne af linjen $b$, så vil man have $ba - a^2 = z''$, en tvetydig ligning, da man for segmentet $a$ kan tage hver af de to rødder. Lad derfor den korrelative ligning være $be - e^2 = z''$. Ved at sammenligne de to ligninger ved hjælp af Viètes metode:
$ba - be = a^2 - e^2$
Ved at dividere begge sider med $a - e$, får man:
$b = a + e$
hvor længderne $a$ og $e$ desuden vil være forskellige.
Hvis man i stedet for arealet $z''$ tager en anden større værdi, dog altid mindre end $\frac{b^2}{4}$, vil segmenterne $a$ og $e$ adskille sig mindre fra hinanden end de foregående, og delingspunkterne vil komme tættere på det punkt, der udgør maksimum for produktet. Jo mere produktet øges, desto mere mindskes forskellen mellem $a$ og $e$, indtil den forsvinder præcis ved den opdeling, der svarer til det maksimale produkt; i dette tilfælde vil der kun være én unik og singulær løsning, hvor de to størrelser $a$ og $e$ bliver ens.
Nu fører Viètes metode, anvendt på de to korrelative ligninger ovenfor, til ligningen $b = a + e$, dermed hvis $e = a$ (hvilket altid vil ske ved punktet, der udgør maksimum eller minimum), vil man, i det givne tilfælde, have $b = 2a$ hvilket vil sige, at hvis man tager midten af segmentet $b$, vil produktet af segmenterne være maksimalt.
- Kildetekst 5 Fermat om maxima og minima. Fra J. Fauvel and J. Gray, eds. (1987). The History of Mathematics: A Reader. London: Macmillan Press Ltd., s. 359–360. Dansk oversættelse ved Clemens Merker.
Newtons fluxionsregning (kildetekst 6) samt forslag til brug i undervisningen
Newton arbejdede ligesom Fermat med kurver. Han opfattede kurver som baner for bevægelser og variable som størrelser, der ændrer sig (flyder) med tiden. Dem betegnede han med bogstaverne $x$ og $y$, og han kaldte dem for fluenter. Man kan tænke på det, som at $x$ og $y$ tilsammen udstikker en banekurve for, f.eks. en partikel, der bevæger sig med tiden, så $x$ spiller rollen af første-koordinaten og $y$ af anden koordinaten i et koordinatsystem. Den hastighed hvormed fluenterne (dvs $x$ og $y$) bevæger sig med, kaldte han for deres fluxioner og betegnede dem ved at sætte en prik over betegnelsen for fluenten, $\dot{x}$ hhv. $\dot{y}$.
I kildetekst 6 kan man se, hvordan Newton arbejdede med fluxioner. Han indledte med at slå fast, at alle problemstillinger omkring kurvers natur, som han skrev, kan reduceres til to problemer:
-
at finde hastigheden af en bevægelse til ethvert givet tidspunkt, når man kender længden af den tilbagelagte strækning,
-
at finde længden af den tilbagelagte strækning, når man kender hastigheden.
I dag ville vi sige, at 1. handler om at finde afledede, altså at differentiere, mens 2. handler om at integrere.
I kildetekst 6 præsenterede Newton sin løsning til problem 1. Han gjorde det ved at angive en algoritme eller en opskrift på, hvordan man kan finde relationen mellem fluxionerne, når man kender relationen mellem fluenterne. Derefter illustrerede han fremgangsmåden på et eksempel, ”Eksempel 1” i kildetekst 6. Umiddelbart virker det måske som det rene hokus pokus, men han giver også en slags bevis i ”Demonstration af løsningen”, der giver samme resultat, som man får ved at følge hans opskrift.
Kildetekst 6
Problem 1
Givet forholdet mellem de flydende størrelser, bestem forholdet mellem deres hastigheder.
Løsning
Opstil ligningen, hvormed det givne forhold er udtrykt, efter dimensionerne af en af de flydende størrelser, lad os antage $x$, og multiplicér dens led med en hvilken som helst aritmetisk progression og derefter med $\dot{x}/x$; udfør denne operation separat for hver af de flydende størrelser. Læg derefter alle produkterne sammen, gør summen lig nul, og du vil få den ønskede ligning.
Eksempel 1
Hvis forholdet mellem de flydende størrelser $x$ og $y$ er $x^3 - ax^2 + axy - y^3 = 0$ orden da først leddene efter dimensionerne af $x$, derefter efter $y$, og multiplicér dem på følgende måde:
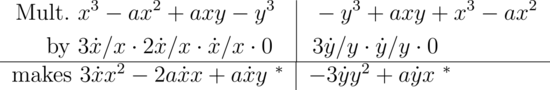
Summen af produkterne er $3\dot{x}x - 2a\dot{x}x + axy - 3\dot{y}y^2 + ayx = 0$ denne ligning giver relationen mellem fluxionerne $\dot{x}$ og $\dot{y}$. Hvis $x$ vælges vilkårligt, vil ligningen $x^3-ax^2+axy-y^3=0$ give $y$; som, når den er bestemt, vil give $\dot{x} : \dot{y} :: 3y^2-ax : 3x^2 -2ax + ay$.[...]
Demonstration af løsningen
Momenterne af flydende størrelser (dvs. deres uendeligt små dele, hvorigennem de kontinuerligt øges i uendeligt små tidsintervaller) svarer til hastighederne af deres forandring eller tilvækst. Hvis momentet af en størrelse, som $x$, repræsenteres ved produktet af dens hastighed $\dot{x}$ med en uendeligt lille størrelse $o$, (dvs. $\dot{x}o$), vil momenterne for de andre størrelser $v, y$ og $z$ blive repræsenteret ved $\dot{v}o, \dot{y}o,\dot{z}o$, fordi $\dot{v}o, \dot{x}o,\dot{y}o$ og $\dot{z}o$ forholder sig til hinanden som $\dot{v}, \dot{x}, \dot{y}$, og $\dot{z}$. Da momenterne $\dot{x}o$ og $\dot{y}o$ er de uendelig små tilvækster af de flydende størrelser $x$ og $y$, som øger disse størrelser over uendelige små tidsintervaller, følger det, at efter et uendelig lille tidsinterval vil $x$ og $y$ være $x+\dot{x}o$ og $y+\dot{y}o$ og derfor vil ligningen, der til enhver tid udtrykker forholdet mellem de flydende størrelser, også udtrykke forholdet mellem $x+\dot{x}o$ og $y+\dot{y}o$, ligesom den gør for $x$ og $y$. Vi kan således erstatte $x$ og $y$ med $x+\dot{x}o$ og $y+\dot{y}o$ i ligningen.
Lad os derfor tage en given ligning: $x^3-ax^2+axy-y^3=0$ og erstatte $x$ med $x+\dot{x}o$ og $y$ med $y+\dot{y}o$ hvilket giver:
$x^3 + 3\dot{x}ox^2 + 3\dot{x}^2oox + \dot{x}^3o^3 - ax^2 - 2axo\dot{x} - a\dot{x}^2oo$
$+ axy + a\dot{x}oy + a\dot{y}ox + a\dot{x}\dot{y}oo - y^3 - 3\dot{y}oy^2 - 3\dot{y}^2ooy - \dot{y}^3o^3 = 0$
Da vi ved, at $x^3 - ax^2 + axy - y^3 = 0$ kanj vi fjerne disse led og vi kan dividere de resterende med $o$. Derved får vi: $3\dot{x}x^2 + 3\dot{x}^2ox + \dot{x}^3oo - 2a\dot{x}x - a\dot{x}^2o + a\dot{x}y + a\dot{y}x + a\dot{x}\dot{y}o - 3\dot{y}y^2 - 3\dot{y}^2oy - \dot{y}^3oo = 0$
Men da $o$ er uendeligt lille, idet det repræsenterer momenterne af størrelserne, vil de led, der er ganget med $o$, være ubetydelige i forhold til de andre led og kan ignoreres. Det efterlader os med: $3x^2\dot{x} - 2 a\dot{x}x + a\dot{x}y + a\dot{y}x - 3\dot{y}y^2 = 0$ som vi også fik i eksempel 1.
Her kan det bemærkes, at de led, der ikke er multipliceret med $o$, altid vil forsvinde; og de led, der er multipliceret med mere end én dimension af $o$, vil også forsvinde. De resterende led, når de divideres med $o$, vil altid antage den form, de skal have ifølge den foregående regel. Q.E.D.
- Kildetekst 6 Newtons fluxionsregning. Uddrag fra D. T. Whiteside (1964). The Mathematical Works of Isaac Newton, Volume 1. Johnson Reprint
Corp. Dansk oversættelse ved Clemens Merker
En læsning af Newtons tekst kunne være i forhold til, hvordan han opfattede de matematiske objekter, han arbejdede med, knyttet an til inspirationen fra fysik og dens betydning for udformningen af den differentialregning, Newton udviklede. En gennemgang af Newtons indførelse af fluenter og fluxioner kan give anledning til en diskussion i undervisningen af, hvordan vi i dag forstår begreber som variable og differentialkvotient, en diskussion der vil have potentiale til at påvirke elevernes begrebsbilleder og –definitioner af disse begreber (se kilde 8 i "Teoretiske konstruktioner"). Der kan arbejdes med Newtons bevis for algoritmen ved at diskutere og tage stilling til, om og i så fald i hvilken forstand – altså efter hvilke kriterier – det kan siges at være et bevis. En sådan diskussion kan lede op til en tilsvarende diskussion om, hvad vi i dag forlanger for at ville acceptere noget som et bevis. I Newtons bevis indgår f.eks. uendelig små størrelser, altså infinitesimaler, så en sådan analyse af Newtons bevis kan give eleverne lejlighed til at forholde sig kritisk til matematisk bevisførelse. Det kan gøres ved at stille spørgsmål som, hvornår argumenteres der f.eks. i forhold til kurven hhv. tangenten, og hvilken betydning har det for stringens? Ville vi i dag acceptere Newtons bevis?
I forhold til de didaktiske teorier præsenteret i 'Teoretiske konstruktioner', har dette potentiale til at bringe meta-diskursive regler omkring matematisk argumentation og bevisførelse frem i lyset og gøre dem til genstand for kritisk refleksion i undervisningen (se kilde 6 og 7 i "Teoretiske konstruktioner"). I en sådan undervisningstilrettelæggelse spiller den historiske kilde en afgørende rolle som en slags ”samtalepartner” fra en anden tid, hvor andre meta-diskursive regler omkring stringens i matematikken var i brug i matematiske miljøer, end dem vi agerer efter i dag. Kildeteksterne kan bruges til at sætte fokus på, at meta-diskursive regler ændrer sig over tid (se kilde 2 og 3 i "Teoretiske konstruktioner" ). Tolkningen og diskussionerne af kildeteksterne kan bidrage til at udvikle elevernes historiebevidsthed i forhold til matematik (se kilde 5 i "Teoretiske konstruktioner").
Leibnizs differentialregning – præsenteret af l’Hôpital (kildetekst 7) samt forslag til brug i undervisningen
Leibniz var inspireret af den omvendte sammenhæng, han fandt mellem differenser og summer. Han betragtede en følge af tal $a_1,a_2,a_3, \dotsc$ og de tilhørende differenser
$b_1 = a_1 - a_2, b_2 = a_2 - a_3, b_3 = a_3 - a_4, \dotsc$
og bemærkede, at hvis man lægger differenserne sammen
$b_1 + b_2 + \dotsc + b_n = a_1 - a_{n+1}$
så er summen lige med differensen mellem første og sidste led i den følge, han startede med. Denne indsigt benyttede Leibniz i forhold til geometriske betragtninger om kurver og deres kvadraturer. Ifølge matematikhistorikeren Henk Bos (Kilde 3, s. 61-62) konkluderede Leibniz fra den inverse sammenhæng mellem summer og differencer, at det at finde kvadraturer (integralregning) og tangenter (differentialregning) er hinandens inverse operationer. Ideen er skitseret i følgende figur, der er gentegnet fra Bos (Kilde 3, s.62):
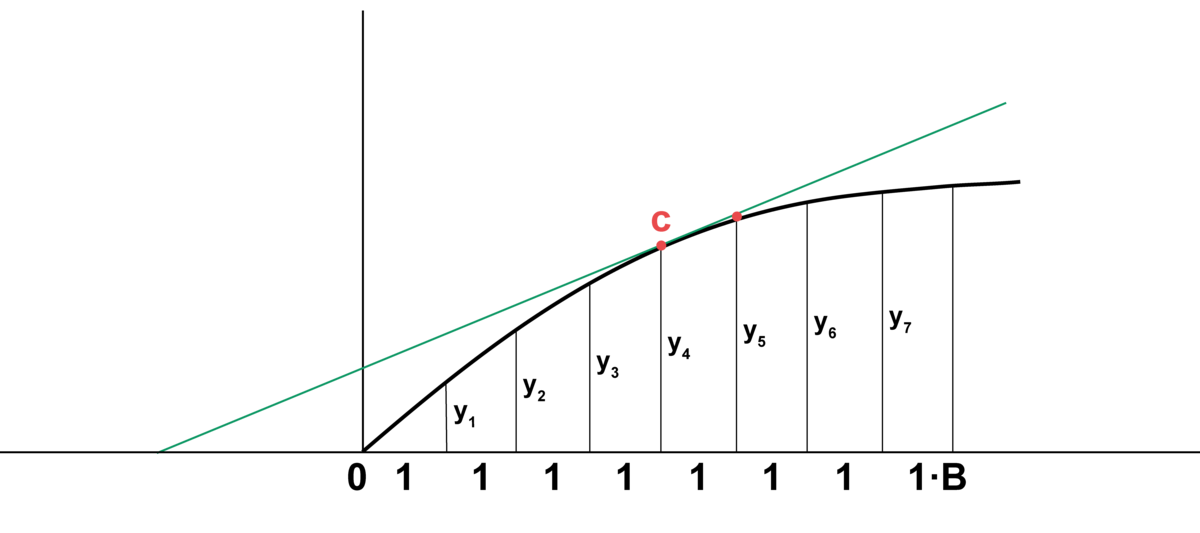
Hvis enheden ”1” vælges uendelig lille, så vil summen af $y$’erne være lig med arealet under kurven, og differensen mellem to på hinanden følgende $y$’er $(y_5 - y_4)$ vil være lig med hældningen af tangenten (i punktet $C$). Det at finde arealer og tangenthældninger er hinandens inverse processer. I dag vil vi mene, at det kræver et grænseværdiargument, men ovenstående illustrerer Leibnizs fremgangsmåde.
En af de helst store fordele ved Leibnizs arbejde er, at han udviklede en notationsform, et symbolsprog, der gjorde det muligt af udvikle regneregler. Han brugte betegnelsen $dx$ og $dy$ for infinitesimaler og udviklede en differentialregning. Det er blevet diskuteret i litteraturen (se f.eks. Kilde 9 og Kilde 3) hvorvidt Leibniz mente, at differentialer eksisterer eller ej. Den gængse holdning er, at han ikke mente, de eksisterede som sådan, men at man kunne regne med dem på en konsistent måde. Det var ikke nemt at læse Leibnizs skrifter, men hans teorier blev udbredt bl.a. gennem en lærebog, der blev skrevet af den franske adelsmand Marquis Guillaume Francois de l’Hôpital (1661-1704). Bogen findes i en dansk kommenterede oversættelse (Kilde 2), og kildetekst 7 er et uddrag herfra.
Kildetekst 7
De uendeligt små størrelsers analyse
Første del om differensregning
Første afsnit hvor reglerne for denne regning gives
DEFINITION I
Størrelser, der uafbrudt vokser eller aftager, kaldes variable størrelser, hvorimod de, der forbliver de samme, medens de andre ændrer sig, kaldes konstante størrelser. I en parabel er ordinaterne og abscisserne således variable størrelser, medens parameteren er en konstant størrelse.
DEFINITION II
Den uendeligt lille del, hvormed en variabel størrelse uafbrudt vokser eller aftager, kaldes differensen.
KOROLLAR
1. Det er klart, at differensen af en konstant størrelse er nul, eller (hvad der er det samme) at konstante størrelser ingen differenser har.
NOTE
I det følgende bruges betegnelsen eller symbolet $d$ til at betegne differensen af en variabel størrelse, som man har udtrykt ved et enkelt bogstav,
[...]
I. KRAV ELLER ANTAGELSE
2. Det kræves, at når to størrelser kun adskiller sig med en uendeligt lille størrelse, kan man uden forskel tage den ene for den anden. Eller (hvad der er det samme) at en størrelse, som kun er forøget eller formindsket med en anden størrelse, der er uendeligt mindre end den selv, kan betragtes som forblivende sig selv.
[...]
NOTE
Det antages sædvanligvis i det følgende, at alfabetets sidste bogstaver $z$, $y$, $x$ etc. betegner variable størrelser, hvorimod de første $a$, $b$, $c$ etc. betegner konstante størrelser, således at: $x$ bliver $x + dx$; $y$, $z$ etc. bliver $y + dy$, $z + dz$ etc., og $a$, $b$, $c$ etc. forbliver de samme $a$, $b$, $c$ etc.
[...]
PROPOSITION I
Problem
4. At tage differensen af flere størrelser, der er lagt til eller trukket fra hinanden.
Lad der være givet $a + x + y - z$, af hvilken differensen skal tages. Hvis det antages, at $x$ forøges med en uendeligt lille del, det vil sige, at den bliver $x + dx$, så bliver: $y$, $y + dy$ og $z$ bliver $z + dz$ medens konstanten $a$ forbliver den samme, $a$. Således bliver den givne størrelse: $a + x + y - z$, $a + x + dx + y + dy - z - dz$, og dens differens, som man finder ved at trække den fra den sidste størrelse, bliver $dx + dy - dz$. Det er ligesådan med de andre, hvilket giver denne regel.
PROPOSITION II
Problem
5. At tage differensen af et produkt frembragt af flere størrelser, der er ganget med hinanden.
1°. Differensen af $xy$ er $y dx + x dy$. Thi når $x$ bliver $x + dx$, bliver $y$, $y + dy$, og xy bliver:
$xy + y dx + x dy + dx dy$,
som er produktet af $x + dx$ og $y + dy$. Produktets differens er:
$ydx + xdy +dxdy$
det vil sige, $y dx + x dy$, fordi $dx dy$ er en uendelig lille størrelse i forhold til de andre led $y dx$ og $x dy$: dividerer man for eksempel $y dx$ og $dx dy$ med $dx$, finder man dels $y$ og dels $dy$, som er $y$'s differens og derfor uendeligt meget mindre end den. Heraf følger, at differensen af et produkt af to størrelser er lig med produktet af den første størrelses differens og den anden størrelse plus produktet af den andens differens og den første.
-Kildetekst 7 Uddrag fra K. Andersens (1988) danske oversættelse.
I afsnittet krav I. kan man se, at l’Hôpital i arbejdet med de uendelig små størrelser (infinitesimaler) tager som udgangspunkt, at forøger man en variabel størrelse $x$ med dens differens $dx$, som ifølge hans Definition II er en uendelig lille størrelse, så er resultatet lig med $x$. Dvs. $x + dx = x$. De kendte regneregler for differentiation kan så genfindes i l’Hôpitals fremstilling af Leibnizs kalkyle. I Proposition II kan vi f.eks. se, hvordan produktregnereglen fremkommer:
$d(xy) = (x + dx)(y + dy) - xy = xy + xdy + ydx + dxdy - xy$
$= xdy + ydx + dxdy = xdy + ydx$
hvor l’Hôpital for at få det sidste lighedstegn smider $dxdy$ væk med den begrundelse, at $dxdy$ er en uendelig lille størrelse i forhold til de andre led.
Leibnizs tilgang til det, vi i dag kalder differential- og integralregning, var således meget anderledes end Newtons. Leibnizs inspiration og intuition er ikke forbundet med hastigheder af flydende størrelser, men kom fra hans arbejder med summer og differenser inden for matematikken selv. For Newton var differentialet en fluxion, en hastighed, mens det for Leibniz var differensen af en variabel og dens uendelig lille tilvækst.
En læsning og sammenligning af de to tekster (kildetekst 6 og kildetekst 7) vil kunne give elever en indsigt i, at matematikere henter deres inspiration og intuition forskellige steder fra såvel uden for som inden for matematikken selv, når de bedriver matematisk forskning. En diskussion af de forskellige opfattelser, Newton og Leibniz havde af de matematiske objekter, de arbejdede med, sammenlignet med, hvordan vi i dag definerer differential- og integralregningens objekter, kan være med til at udvikle elevernes begrebsbilleder og –definitioner (se kilde 8 i "Teoretiske konstruktioner"). Dertil kommer, at Leibnizs udvikling af notation viser styrken i at have et veludviklet matematisk symbolsprog.
I forhold til stringent bevisførelse vil vi i dag sige, at Leibnizs argumentation lider af de samme mangler som Newtons i forhold til deres brug af uendelige små størrelser. Hvis man inddrager den franske matematiker Augustin Louis Cauchy og hans lærebog i analyse, vil man kunne dykke videre ned i analysens grundlag og præsentere eleverne for den videre udvikling mod noget, der begynder at minde om det, de vil møde på videregående matematikbaserede uddannelser. Cauchys lærebog var skrevet til undervisningen på den parisiske ingeniørskole École Polytechnique, og her kan man se, hvordan han definerede begreber som variable, grænseværdi, kontinuitet, den afledede og integralet. Det kan man finde inspiration til i nogle af de kildestyrede projekter og undervisningsforløb, der er designet i TRIUMPH-projektet (projektorienterede undervisningsforløb med refleksionsspørgsmål og lærerstyret læsevejledning af uddrag af kildetekster kan findes her https://blogs.ursinus.edu/triumphs/) og i undervisningsforløbet om Cauchys integraler, der er udviklet af gymnasielærere i en dansk kontekst og beskrevet i LMFK-bogen redigeret af Danielsen og Sørensen (Kilde 4).
Eksempel III: Funktionsbegrebets udvikling
Hverken Fermat, Newton eller Leibniz arbejdede med funktioner. Funktionsbegrebet kom først på banen midt i 1700-tallet med den schweiziske matematiker Leonard Euler (1707-1783). I det følgende vil vi præsentere korte uddrag af kildetekster fra Eulers og den tyske matematiker Johann Peter Gustav Lejeune Dirichlets (1805-1859) definitioner af funktioner. Vi viser, hvordan disse kildetekster har været brugt i gymnasiets matematikundervisning til at give eleverne indsigt i, hvordan et centralt matematisk begreb som funktionsbegrebet er skabt gennem en længere udviklingsproces og derved udvikle deres historiebevidsthed i forhold til matematik. Samtidig kan arbejdet med dette emne og disse kildetekster understøtte elevernes matematiklæring jævnfør de didaktiske teorier, der er introduceret i "Teoretiske konstruktioner" (se specifikke litteraturhenvisninger i de forskellige afsnit nedenfor). Den historiske udvikling og kildeteksterne vil ikke blive gennemgået som sådan, i stedet henvises til Kjeldsens kapitel om funktionsbegrebets udvikling i gymnasielærebogssystemet Teori og Redskab (Kilde 11) og Petersens speciale (Kilde 19).
Eulers funktionsbegreb (kildetekst 8) samt forslag til brug i undervisningen
Det var Leonard Euler, der formulerede differential- og integralregningen i termer af funktioner i stedet for kurver. Han præsenterede sin første definition af funktionsbegrebet i sin bog Introductio in Analysin Infinitorum fra 1748. Kildetekst 8 er et uddrag af kapitel 1, hvori Euler præsenterede sit funktionsbegreb. Som vi kan se, definerede han en funktion af en variabel størrelse, som et analytisk udtryk, og han definerede en variabel som en størrelse, der kan antage alle værdier uden undtagelser.
Kildetekst 8
Kapitel 1
Om funktioner generelt
- En konstant størrelse er en fastlagt størrelse, der altid bevarer samme værdi.
- En variabel størrelse er en, der ikke er fastlagt eller er universel, den kan antage enhver værdi.
- En variabel størrelse fastlægges, når den tilskrives en bestemt værdi.
- En funktion af en variabel størrelse er et analytisk udtryk, der på en vilkårlig måde er sammensat af den variable størrelse og tal eller konstante størrelser.
Derfor vil ethvert analytisk udtryk, hvori der udover variablen $z$ kun indgår konstante størrelser, være en funktion af $z$. Da er $a +3z$, $az - 4z^2$, $az + b\sqrt{a^2-z^2}$, $c^z$ osv. alle funktioner af $z$ - Da vil en funktion af en variabel størrelse, ligeledes være en variabel størrelse.
-Kildetekst 8 Eulers (1748) præsentation af sit variabel- og funktionsbegreb. Dansk oversættelse ved Clemens Merker
Sammenligner vi Eulers første funktionsbegreb (kildetekst 8) med vores eget, er der nogle forskelle, der springer i øjnene. For det første forlangte Euler, at funktioner skal være givet ved en formel, ét analytisk udtryk, og for det andet er vore dages definitionsmængde ikke en del af Eulers funktionsbegreb. Eulers variabelbegreb gør, at variable og dermed funktioner ikke kan indskrænkes til f.eks. et interval. Variable og dermed funktioner er defineret overalt. Dette kaldes i litteraturen (Kilde 16) for den variables generalitet. Analyserer vi det i forhold til Sfards didaktiske teori (se kilde 6 og 4 i "Teoretiske konstruktioner" ) er den variables generalitet en meta-diskursiv regel i Eulers opfattelse af matematik.
En anden af Eulers meta-diskursive regler var, at matematik skulle kunne håndtere alle fysiske situationer. Dette kom til udtryk i diskussion om den svingende streng mellem især Euler og den franske matematiker Jean le Rond d’Alembert (1717-1783). Eulers første funktionsbegreb kom her til kort, da det f.eks. ikke kunne beskrive en knipset streng:

Eulers ”løsning” var at udvide funktionsbegrebet, til det han kaldte for kontinuerte funktioner og diskontinuerte funktioner. De kontinuerte funktioner var dem, der kunne beskrives ved ét analytisk udtryk i overensstemmelse med hans første funktionsbegreb i kildetekst 8. Ved diskontinuerte funktioner forstod han bl.a. dem, der kunne beskrives ved at sammenstykke forskellige analytiske udtryk. Det gælder f.eks. en knipset streng, der er stykkevis lineær. Med begrebet diskontinuert mente Euler således ikke det samme, som det vi i dag forstår ved diskontinuerte funktioner.
Inddragelse af Eulers funktionsbegreber i undervisningen har således potentiale til dels at sætte fokus på funktionsbegrebet som sådan, og dels anskueliggøre konkrete meta-diskursive regler, der har ændret sig over tid. I 2010-2011 blev dette bl.a. testet i undervisningsforløbet ”Funktionsbegrebet set med historiske og nutidige briller” i en 2.g klasse. Resultaterne fra forløbet er publiceret i Kilde 15. Hele forløbet er argumenteret og beskrevet i Kilde 19 inklusiv arbejdssedler til eleverne og organisering af gruppearbejde mm. Det viste sig bl.a., at adskillige af eleverne havde samme funktionsbegreb som Eulers første funktionsbegreb, hvilket forklarede deres manglende forståelse af betydningen af definitionsmængden i det funktionsbegreb, de blev introduceret til i deres lærebog. I forhold til Talls og Vinners teori om begrebsbillede og –definition (se kilde 8 i "Teoretiske konstruktioner") kom eleverne i situationer, hvor konfliktende faktorer blev aktiveret samtidig. Det skete i diskussioner af forskellene på Eulers funktionsbegreber og funktionsbegrebet fra deres lærebog, diskussioner der også bragte deres eget funktionsbegreb frem i lyset og synliggjorde konfliktfaktorer.
Dirichlets funktionsbegreb (kildetekst 9) samt forslag til brug i undervisningen
I litteraturen tilskrives vore dages funktionsbegreb ofte den tyske matematiker Johann Peter Gustav Lejeune Dirichlet (1805-1859). I kildetekst 9 ses en oversættelse af en definition, han formulerede i en tekst fra 1837. Her er det kontinuerte funktioner, men kontinuitet var ikke en del af hans definitionsbillede, i praksis så han stort på kontinuitetsegenskaben i definitionen af funktioner.
Kildetekst 9
Lad os antage, at $a$ og $b$ er to bestemte værdier, og at $x$ er en variabel størrelse, der gradvist antager alle værdier mellem $a$ og $b$. Hvis der til ethvert $x$ hører et entydigt og endeligt $y$, således at når $x$ kontinuerligt bevæger sig igennem intervallet fra $a$ til $b$, så varierer $y=f(x)$ sig ligeledes gradvist, så kaldes $y$ en kontinuert [...] funktion af $x$ i dette interval. Det er derudover på ingen måde nødvendigt, at $y$ afhænger af $x$ efter samme forskrift i hele dette interval. Det er endda ikke nødvendigt kun at tænke på sammenhænge, der kan udtrykkes ved matematiske operationer.
-Kildetekst 9 Diriclets (1837) funktionsdefinition. Dansk oversættelse ved Clemens Merker
Sammenligner vi med Eulers funktionsbegreb, kan vi se at Dirichlet, i modsætning til Euler, forlangte entydighed: til et hvert $x$ i intervallet mellem $a$ og $b$ skal der være et og kun et $y$, altså en entydigt bestemt funktionsværdi. En anden forskel er, at Dirichlet ikke var styret af meta-reglen om den variables generalitet. Han opererede med det, vi vi dag ville kalde en defintionsmængde. For det tredje lagde han eksplicit vægt på, at funktioner ikke behøver at kunne udtrykkes ved matematiske formler.
I undervisningsforløbet ”Funktionsbegrebet set med historiske og nutidige briller” (Kilde 19) blev eleverne bedt om at sammenligne Eulers, Dirichlets og deres lærebogs definitioner af funktionsbegrebet. Det gav, som beskrevet ovenfor i forbindelse med Eulers funktionsbegreb, anledning til at konfliktfaktorer i elevers begrebsbillede blev aktiveret i diskussionerne elever imellem og i diskussioner mellem læreren og elever. Derudover kom der flere meta-diskursive regler frem i lyset, som nogle af eleverne var styret af, og som ikke er en del af diskursen i det matematiske samfund. I en af dialogerne eleverne imellem blev det f.eks. klart, at nogle af eleverne forbandt bogstaverne $a$ og $b$ i Dirichlets tekst (kildetekst 9) med hældningskoefficient og skæring med $y$-aksen for en lineær funktion (Kilde 14 og 15). Endelig gav kildeteksterne og elevernes lærebogsbeskrivelse af funktionsbegrebet sammen med den historiske diskussion om den svingende streng eleverne indblik i forskningsprocesser i matematik, samt erfaringer med at matematikkens begreber udvikler sig over tid og er genstand for diskussioner matematikere imellem.
til: GYMNASIET
emne: MATEMATIKHISTORIE
UDGIVET: 2025
Forfatter
Tinne Hoff Kjeldsen
Professor
Københavns Universitet
Uffe Thomas Jankvist
Professor
DPU, Aarhus Universitet
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Andersen, K., Andersen, I., Garm, K., Holth, K., Jacobsen, I. T., & Mejlbo, L. (1986). Kilder og kommentarer til ligningernes historie. Vejle: Forlaget Trip.
- Andersen, K. (1988). Analyse af de uendeligt små størrelser til forståelse af kurver (kommenteret dansk oversættelse af L’Hôpital, G. F. A. (1696). Analyse des infiniment petits pour l’intelligence des lignes courbes. Århus: Foreningen Videnskabshistorisk Museums Venner.
- Bos, H. J. M. (1980). Newton, Leibniz and the Leibnizian Tradition. I: I. Grattan-Guinness (Ed.) From the Calculus to Set Theory, 1630-1910. An Introductory History, s. 49-93. Princeton and Oxford: Princeton University Press.
- Danielsen, K. & Sørensen, H. K. (Eds.) (2018). Snows spøgelseskort, Halleys livrenter og Cauchys integraler: Tre gode matematikhistorier. Vojens: Matematiklærerforeningen.
- Dirichlet, J. P. G. L. (1837). Über die darstellung ganz wilkürlicher functionen durch sinus- und cosinusreihen. Repertorium der Physik, Bd. I, s. 152–174.
- Euler, L. (1748). Introductio in nalysin infinitorum (2 vols), Lausanne. Engelsk oversættelse af John D. Blanton (1988): Introduction to Analysis of the Infinite - Book I. Springer-Verlag, 1988.
- Frandsen, J. (1996). Ægyptisk matematik. Systime.
- Fauvel, J. & Gray, J. (Eds.) (1987). The History of Mathematics: A Reader. London: Macmillian Press Ltd.
- Guicciardini, N. (2003). Newton’s Method and Leibniz’s Calculus. I: H. N. Jahnke (Ed.) A History of Analysis, s. 73-103. Providence Rhode Island: American Mathematical Society.
- Høyrup, J. (1998). Algebra på Lertavler. Matematiklærerforeningen.
- Jensen, S. & Sørensen, K. (1988). Teori og Redskab, vol. 1 (kapitel 9). København: Christian Ejlers forlag.
- Jensen, S. & Sørensen, K. (1989). Teori og Redskab, vol. 3 (kapitel 8). København: Christian Ejlers forlag.
- Katz, V. (2007) (Ed.) The Mathematics of Egypt, Mesopotamia, China, India and Islam: A Sourcebook. Princeton University Press.
- Kjeldsen, T. H. & Petersen, P. H. (2012). History and the Learning of Mathematics: Detecting student’s meta-discursive rules. Proceedings of ICME 12: The 12th International Congress on Mathematical Education.
- Kjeldsen, T. H. & Petersen, P. H. (2014). Bridging History of the Concept of Function with Learning of Mathematics: Students' Meta-Discursive Rules, Concept Formation and Historical Awareness. Science & Education, 23(1), 29-45.
- Lützen, J. (1978). Funktionsbegrebets udvikling fra Euler til Dirichlet. Nordisk Matematisk Tidskrift, Vol. 25/26, No. 1 (1978), s. 5-32. https://www.jstor.org/stable/24525259
- Lützen, J. & Ramskov, K. (1999). Kilder til matematikkens historie. København Institut for Matematiske Fag. https://noter.math.ku.dk/matematik.htm
- Pedersen, K. M. (1980). Techniques of the Calculus, 1630-1660. I: I. Grattan-Guinness (Ed.) From the Calculus to Set Theory, 1630-1910. An Introductory History, s. 10-48. Princeton and Oxford: Princeton University Press.
- Petersen, P. H. (2011). Potentielle vindinger ved inddragelse af matematikhistorie i matematikundervisningen. Roskilde: Roskilde Universitet. IMFUFAtekst, nr. 483. Specialeafhandling. http://thiele.ruc.dk/imfufatekster/pdf/483web.pdf
- Sfard, A. (2008). Thinking as Communicating. Cambridge: Cambridge University Press.
- Struik, D. J. (1969). A Source Book in Mathematics. 1200-1800. Cambridge Mass.: Harvard University Press.
- Tall, D. & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151-169.
- Whiteside, D. T. (1964). The Mathematical Works of Isaac Newton, Volume 1. Johnson Reprint Corp.