Hvad er matematikforestillinger (beliefs)?
Det er veldokumenteret, at de forestillinger, som elever gør sig om, hvad matematik er, kan og handler om, kan have en afgørende indflydelse på deres tilgang til faget, deres motivation og ikke mindst deres lyst til at lære matematik. Nogle matematikforestillinger kan endda være hindrende for læring. Det kan for eksempel være en forestilling om, at “matematik kun kan læres af dem, der har et medfødt talent”, “matematik er meget svært”, eller “matematik handler kun om udenadslære”. Andre matematikforestillinger kan til gengæld være gavnlige i en læringssituation, såsom at “det er okay at prøve sig frem i problemløsning, indtil jeg finder en bedre strategi”, eller “matematik er noget, jeg kan anvende i min dagligdag”.
Sådanne matematikrelaterede forestillinger kalder man inden for det matematikdidaktiske forskningsfelt for beliefs. En persons beliefs er de forestillinger, man gør sig om, hvad der er sandt i forhold til et emne, et objekt eller et fænomen. Det er dog ikke nødvendigvis en objektiv sandhed, der er tale om, men personens subjektive overbevisning om, hvad der er sandt. Ofte stiller man ikke selv spørgsmålstegn ved disse “sandheder,” men opdager måske først, at man er galt på den, når man på en eller anden måde bliver konfronteret med, at der kan være en anden måde at anskue tingene på.
En ofte anvendt definition af beliefs er udarbejdet af Philipp (2007) og baseret på en omfattende gennemgang af litteraturen om elev- og lærerbeliefs. I denne sammenhæng defineres beliefs som "de linser, man ser igennem, når man fortolker verden" (s. 258, vores oversættelse).
Beliefs forstås som:
(…) psykologisk forankrede opfattelser, præmisser eller udsagn om verden, som man anser for at være sande. De er mere kognitive, mærkes mindre intenst og er sværere at ændre end holdninger. Beliefs kan betragtes som linser, der påvirker ens opfattelse af en given del af verden, eller som dispositioner til handling. I modsætning til viden kan beliefs variere i graden af overbevisning og er ikke konsensusbaserede. Beliefs er mere kognitive end følelser og holdninger (Philipp, 2007, s. 259, vores oversættelse).
Sammenholdt med nærliggende begreber er beliefs altså mere rodfæstede og kognitive end holdninger og følelser, som kan ændre sig forholdsvist hurtigt. Det tager med andre ord længere tid og kræver en større indsats at ændre beliefs. Også viden er tæt forbundet med beliefs. Men hvor viden er karakteriseret ved, at der er en generel enighed om validiteten af denne, så er dette ikke nødvendigvis tilfældet, når det kommer til beliefs. Hvor viden således er noget, der er officielt eller objektivt bekræftet, så er det op til den enkelte at vurdere sandhedsværdien af sine beliefs. Man vil som hovedregel ikke være 100% sikker på sandheden af sine beliefs, og man kan have visse beliefs, som man tror mere på end andre. Det betyder, at hvad der anses som viden for én person, kan være beliefs for en anden. For eksempel kan en elev have den forestilling, at der altid kun kan findes ét korrekt resultat af et matematisk problem, mens en anden elev for eksempel har erfaringer med andengradsligninger og derfor ved, at det ikke altid er tilfældet. Det er dog muligt, at man i visse tilfælde opfatter nogle af sine beliefs som objektivt sande – og dermed regner dem for at være viden – indtil de bliver modbevist. Dog vil mange beliefs have en karakter, som gør, at de aldrig kan blive til viden, simpelthen fordi der ikke findes en objektiv sandhed om emnet. Det kan for eksempel være beliefs om matematikkens oprindelse, om hvad det vil sige at være god til matematik, eller hvordan man opfatter sig selv som matematikelev. Ydermere kan man godt besidde modstridende beliefs, hvilket ikke er tilfældet, når det kommer til viden. Modstridende beliefs kan eksistere, så længe de ikke bliver konfronteret med hinanden, hvorfor de typisk vil være relaterede til forskellige kontekster. For eksempel kan man opfatte matematik som irrelevant og ubrugeligt i dagligdagen, når man har matematik i skolen, men have en helt anden opfattelse, når man løser en sudoku, udregner rabatten på en vare i supermarkedet eller justerer en strikkeopskrift.
Hvordan opstår beliefs?
Både erfaringer (observation eller deltagelse) og kultur (overtagelse af andres beliefs) bidrager til skabelsen af beliefs. Når man møder verden og gør sig erfaringer med dens forskellige fænomener, drager man slutninger og konklusioner, som hjælper én til at forstå omgivelserne (Pajares, 1992). Bekræftes disse konklusioner af de sociale omgivelser og af nye erfaringer, forstærkes de og bliver til beliefs. Dermed fungerer beliefs som en slags filter, der hjælper med at simplificere en kompleks verden. Det betyder også, at de tidligt dannede beliefs er med til at “farve” og dermed påvirke efterfølgende indtryk og erfaringer. En person vil altid anse sin første opfattelse af et fænomen som værende sand og vil ikke betvivle eller ændre den, medmindre den er i konflikt med nye informationer eller oplevelser. Jo flere gange beliefs bliver bekræftet, jo mere robuste bliver de – og jo større er sandsynligheden desuden for, at de danner grundlag for nye beliefs (Op’t Eynde et al., 2002).
I en læringssammenhæng betyder dette, at hvis en elevs første erfaringer med for eksempel faget matematik bliver bekræftet løbende gennem skoletiden, vil elevens beliefs om matematik blive mere robuste og særdeles svære at ændre – sommetider endda selvom eleven præsenteres for modstridende information.
Hvad sker der, når virkeligheden ikke matcher ens beliefs?
Sker dette – at man præsenteres for en eller anden form for information, som ikke passer med de beliefs, man allerede har – igangsættes typisk en evaluering, hvor man sammenligner sine eksisterende beliefs med den nye information. Er modstriden så stor, at den ikke kan forklares, opstår der en kognitiv konflikt mellem de eksisterende beliefs og den nye information. Eftersom man altid vil søge efter konsistens i sine beliefs (Op’t Eynde et al., 2002), må en sådan konflikt bringes til løsning, hvilket kan ske på flere måder:
- Man kan for eksempel vælge at afvise den nye information. Måske er den nye information ikke overbevisende nok, måske kan den affejes med, at det er et helt særligt tilfælde, eller måske er de eksisterende beliefs så centrale, at det vil have for store omkostninger (konsekvenser for andre relaterede beliefs) at ændre dem.
- En anden mulighed er, at man fortolker eller modificerer den nye information på en måde, så den passer til de eksisterende beliefs.
- Det kan også være, at man i sammenligningen af den nye information og de beliefs, man allerede har, vurderer, at man er nødt til at modificere sine beliefs, så den nye information kan inkluderes.
- Som absolut sidste alternativ kan man afvise sine eksisterende beliefs og skifte dem ud med nye, som passer til den nye information. Den sidste mulighed er naturligvis den mest indgribende og derfor også den, som man så vidt muligt vil forsøge at undgå ved at vælge en af de tre andre muligheder. I det hele taget vil ændringer eller udskiftninger af beliefs påvirke hele den pågældende klynge af beliefs – og måske endda også hele ens såkaldte “beliefssystem,” afhængigt af hvor centrale de ændrede beliefs er (Rolka & Roesken-Winther, 2015).
Green (1971) pointerer, at noget af det, der kan være med til at afgøre, hvor tilbøjelig man er til at tilpasse eller ændre ens beliefs, når noget tyder på, at de ikke matcher med virkeligheden, er, hvorvidt de er baseret på evidens eller ej. Beliefs, som understøttes af eksempler og erfaringer, er lettere at ændre på baggrund af nye erfaringer, bedre evidens, modbeviser m.v. Modsat vil beliefs, som ikke er baseret på evidens, men som for eksempel er overtaget fra andre eller er opstået i en kulturel sammenhæng (for eksempel ”matematik er kun noget, virkelig intelligente mennesker kan lære”), være markant sværere at ændre med rationel kritik, refleksion osv. Green anskueliggør de ikke-evidensbaserede beliefs som den slags, hvor man kan finde på at indvende: ”Jeg er ligeglad med fakta, jeg har allerede besluttet mig!”.
Et illustrativt eksempel på en sådan belief kan findes i casen om 1.g-eleven “Lucas” (Næs, 2024), som insisterer på, at et kvadrat ikke er et rektangel, da det strider imod det, han har lært om rektangler i grundskolen, nemlig at der altid er to sider, der er længere end de to andre. Selv efter en gennemgang af logiske ræsonnementer, hvor Lucas rent faktisk medgiver, at et kvadrat rent logisk også er et rektangel, holder han fast i sin overbevisning: “Om det er forkert eller ej, så vil jeg alligevel fastholde, at mit svar er nej”. For Lukas synes konsekvensen ved at ændre denne forestilling uoverskuelig, idet han mener, at han så må tvivle på flere andre ting, han har lært (eller fået fortalt) i grundskolen.
Beliefssystemer
Som nævnt er beliefs altid organiseret i beliefssystemer (Green, 1971). Disse består af såvel bevidste som ubevidste beliefs, samt hypoteser og forventninger, som en person knytter til et bestemt objekt, fænomen eller emne. Systemet af eksisterende beliefs udgør således det filter, som ny information eller nye erfaringer opfattes igennem. Beliefs er altså i høj grad relateret til andre beliefs og optræder derfor ikke uafhængigt af hinanden. Green (1971) beskriver, hvordan beliefssystemer er karakteriseret ud fra tre forhold:
Forhold 1: Indbyrdes afhængighed
Et beliefssystem er opbygget ud fra en quasi-logik, hvilket betyder, at de beliefs, der udgør systemet – i modsætning til viden – ikke er logisk organiseret ud fra deres indhold, men i stedet er organiseret ud fra, hvordan de forstås og relateres indbyrdes af personen. I en sådan quasi-logisk struktur vil nogle beliefs være primære, og andre vil være afledte af disse. For eksempel kan en primær belief være, at ”matematiske evner er medfødte”, hvilket kan føre til en afledt belief om, at ”jeg er ikke født med matematiske evner, så jeg kan lige så godt lade være med at forsøge at lære matematik”.
Forhold 2: Grad af overbevisning
Nogle beliefs betyder mere for en person end andre, hvilket afhænger af den psykologiske centralitet. Sådanne centrale beliefs synes vigtigere og stærkere end mere perifere beliefs og er dermed sværere at ændre på. Des mere central, en belief er, des større konsekvenser vil en ændring have for resten af beliefssystemet. I forhold til ovennævnte eksempel om matematiske evner som noget medfødt, så kan den afledte belief om egne evner have central psykologisk betydning for personen, da den måske fungerer som en forklaring på knap så gode præstationer, hvilket dermed fritager personen for ansvar. Da de mere perifere beliefs som nævnt er lettere at ændre, kan det forekomme, at nogle af disse ikke ”passer” til de mere centrale beliefs. For eksempel kan elevers perifere beliefs om matematikundervisning godt ændres ved en undersøgende tilgang samtidig med, at eleverne har en dybere og mere central forestilling om matematik som noget, der er baseret på regler og udenadslære.
Forhold 3: Klyngestruktur
Som nævnt er beliefs aldrig uafhængige af hinanden, men optræder i stedet altid i klynger inden for beliefssystemet (Green, 1971). Det gør det muligt at besidde modstridende beliefs, så længe de tilhører forskellige klynger og ikke bliver konfronteret med hinanden. Ofte vil det i praksis betyde, at de pågældende beliefs er knyttet til forskellige kontekster og derfor ikke aktiveres på samme tid.
Elevers beliefssystem om matematik kan siges at bestå af forskellige klynger eller dimensioner, som både knytter sig til matematik som skolefag og i dagligdagen, til elevens egen måde at se sig selv som matematikelev på osv. På baggrund af tidligere forskningskategoriseringer af elevers matematikrelaterede beliefs opstillede Op’t Eynde et al. (2002) tre dimensioner i elevers beliefssystem om matematik:
- Beliefs om matematikundervisning, herunder beliefs om matematik som fag, matematisk læring og undervisning og matematisk problemløsning.
- Beliefs om selvet (i en matematikrelateret situation), herunder beliefs om egne evner, såkaldt “self-efficacy” (tiltro til egne evner), selvkontrol, målorientering og værdien af opgaveløsning.
- Beliefs om den sociale kontekst (klassen), herunder beliefs om lærerens og elevens rolle og funktion samt de sociale og sociomatematiske normer i klassen. De sociomatematiske normer (Yackel & Cobb, 1996) er de normer, der etableres i klasserummet for, hvad der anses for eksempelvis at være værdifulde bidrag til en matematisk samtale, hvad der udgør et fyldestgørende matematisk svar eller argument, hvad der skal til for at et løsningsforslag regnes for værdifuldt etc. Sådanne normer er stærkt relateret til – både elevers og læreres – beliefs om matematik, i og med at de både opstår på baggrund af beliefs og samtidig medvirker til at forme elevers beliefs. På samme måde inkluderer denne dimension også de forventninger, der knytter sig til Brousseaus (1997) begreb om den didaktiske kontrakt, der beskriver de – ofte uudtalte – forventninger, som lærer og elever har indbyrdes til hinanden i klasserummet om for eksempel arbejdsfordeling, opførsel, ansvar, frihedsgrader m.v. Disse forventninger udspringer både fra de kulturelle normer, der findes om skolen som institution, fra den implicitte magtbalance, der er mellem elever og lærer, og fra de erfaringer, vaner og rutiner, som opbygges gennem skoletiden. Både elevernes og lærerens matematikrelaterede beliefs vil have indflydelse på den didaktiske kontrakt. Omvendt ligger der også et potentiale i den didaktiske kontrakt – og i mulige brud på den – til at påvirke og udvikle bestemte beliefs om matematik hos eleverne.
For også at inkludere beliefs, der ikke nødvendigvis er relateret til matematik i en skolesammenhæng har Jankvist (2015) senere foreslået en fjerde dimension:
- Beliefs om matematik som disciplin, herunder beliefs om matematik som ren såvel som anvendt videnskab, om matematik som et system af redskaber til samfundsmæssig anvendelse, samt om matematiske begrebers og teoriers filosofiske og epistemologiske natur (Jankvist, 2015). Det er således i denne dimension, vi for eksempel finder elevernes forestillinger om, hvor matematikken stammer fra, hvad den bruges til og hvor, hvad en matematiker beskæftiger sig med, og hvad der karakteriserer matematik som videnskab.
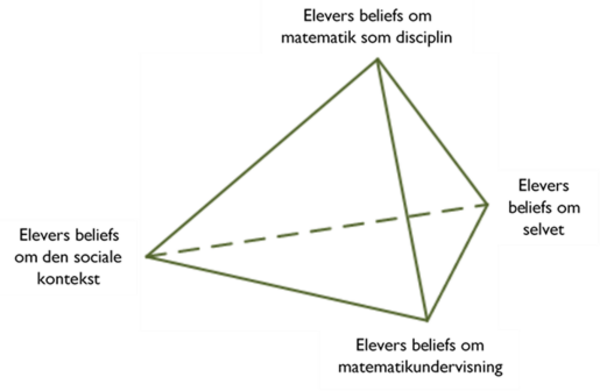
Tilsammen danner de fire dimensioner altså elevers matematikrelaterede beliefssystem, hvilket er illustreret i Figur 1 nedenunder, hvor de tre oprindelige dimensioner, som primært har at gøre med matematik i en uddannelsesmæssig kontekst, udgør ”bunden” i et tetraeder, hvilket signalerer, at beliefs om matematik som disciplin bygger på og udvikles gennem de beliefs, der opbygges i skolen.
Er nogle beliefs bedre end andre?
Forskning peger på, at nogle beliefs ser ud til at være mere eller mindre favorable i forhold til elevers forhold til matematikfaget og deres tilgang til matematikken. Det er centralt, at de beliefs, der udvikles, baseres på evidens. Som nævnt vil evidensbaserede beliefs være modtagelige over for justeringer og ændringer, hvis man præsenteres for bedre evidens, modstridende information eller rationel kritik (Green, 1971). At gøre elever åbne over for at blive klogere, mere indsigtsfulde eller nuancerede i deres opfattelse af verden kræver altså, at vi præsenterer dem for evidens i form af eksempler, erfaringer og mulighed for refleksion.
Med udgangspunkt i litteraturen opstiller Schoenfeld (1992, s. 359, vores oversættelse) en liste over beliefs, som har negativ betydning for elevers matematiske problemløsning:
- Matematiske problemer har ét og kun ét rigtigt svar.
- Der er kun én korrekt måde at løse et matematisk problem – som regel den, som læreren for nylig har vist klassen.
- Helt almindelige elever kan ikke forventes at forstå matematik; de må nøjes med at lære det udenad og anvende det, de har lært, mekanisk og uden forståelse.
- Matematik er en aktivitet, man udfører alene.
- Elever, som har forstået den matematik, de er blevet undervist i, vil kunne løse ethvert problem på fem minutter eller mindre.
- Den matematik, man lærer i skolen, har intet eller meget lidt at gøre med den virkelige verden.
- Formelle beviser er irrelevante for nye opdagelser eller opfindelser.
Flere matematikdidaktiske forskere beskriver forskellige opfattelser af matematikken ved hjælp af et spektrum, som kan siges at gå fra et dualistisk perspektiv i den ene ende til et relativistisk perspektiv i den anden (Figur 2). Det dualistiske perspektiv er karakteriseret ved at se matematik som noget, der er statisk og regelbaseret, som primært handler om at finde resultater ved hjælp af udenadslære, og som mest af alt hører til i skolen. Omvendt bygger det relativistiske perspektiv på, at matematik er et dynamisk og sammenhængende system, som bygger på begreber, principper og generaliseringer, logisk tankegang og forståelse, og som kan anvendes i virkeligheden.

De beliefs, som Schoenfeld oplister, er således udtryk for et dualistisk perspektiv på matematik. Adskillige studier peger på, at et mere relativistisk syn på matematik er relateret til højere motivation, større glæde ved matematikfaget, bedre præstationer og et positivt fagligt selvbillede. Noget tyder på, at de dualistiske beliefs ikke blot er særdeles udbredte (f.eks. Østergaard, 2022), men også i høj grad stammer fra matematikundervisningen i skolen.
I det hele taget peger forskningen på, at elevers beliefs om matematik både dannes, udvikles og manifesteres i klasselokalet, og at det derfor er helt essentielt, at der er overensstemmelse med den måde, vi ønsker, at eleverne opfatter matematikken på, og de signaler, vi sender med tilgangen til matematikken i undervisningen. Ernest (2015) foreslår fire visionære målsætninger for matematikundervisningen, som skal bidrage til:
Elevers matematiske selvtillid
At opleve succes i og med matematik kan være afgørende for elevers holdning og tilgang til faget. Når de føler sig selvsikre i deres matematiske viden og kunnen, når de har en oplevelse af, at de er stand til at erhverve sig ny viden, og når de forbinder matematik med positive erfaringer, vil de højst sandsynligt være mere vedholdende, når de arbejder med problemløsning, og de vil være mere tilbøjelige til at tage imod vanskelige udfordringer i stedet for at give op. Ofte vil det have en selvforstærkende effekt, eftersom eksempelvis det at lykkes med at løse svære problemer kan give nye succesoplevelser og dermed bidrage til en endnu højere faglig selvtillid og en mere positiv holdning. Matematiklærere bør derfor være yderst opmærksomme på at inddrage overvejelser om sådanne følelsesmæssige aspekter i undervisningen.
Socialt engagement og myndiggørelse
Ernest peger på vigtigheden af, at elever bliver opmærksomme på matematikkens rolle i samfundet, både politisk, socialt og personligt. Ydermere skal de lære at forholde sig kritisk til den, blandt andet ved at inddrage “kritik af svar, metoder, grafer, argumenter, modeller etc.” (s. 191, vores oversættelse) i matematikundervisningen.
Matematisk kreativitet gennem problemformulering og -løsning.
Løsning af problemer i matematikundervisingen kan ofte have karakter af rutineopgaver. Men ifølge Ernest har arbejdet med matematiske problemer potentiale til at gøre matematik til et yderst kreativt fag, hvor eleverne får lov til at bruge deres fantasi, opdage nye sider af matematikken og finde på nye tilgange og metoder. Særligt det at formulere matematiske problemer er en ofte underprioriteret aktivitet i undervisningen, men her er der rige muligheder for, at eleverne kan opdage relationer mellem matematiske begreber, arbejde med matematiske modeller og inddrage mange forskellige og motiverende aspekter af deres eget liv.
En bredere påskønnelse af matematik
Særligt dette mål kan siges at være relateret til elevers beliefs, og Ernest anbefaler, at matematikundervisningen giver eleverne mulighed for at opnå en øget bevidsthed om følgende aspekter (Ernest, 2015, s. 191-192, vores oversættelse):
- At matematik er “et centralt element i kulturen, kunsten og livet, i nutiden og i fortiden, som gennemsyrer og underbygger naturvidenskab, teknologi og alle aspekter af menneskelig kultur”.
- “[M]atematikkens historiske udvikling, de sociale kontekster, hvori matematikkens begreber er opstået, samt dens symbolisme, teorier og problemer”.
- At matematik er “en unik disciplin med dens centrale grene og begreber såvel som deres sammenkoblinger, indbyrdes afhængighed og dens overordnede sammenhæng".
- “Måden, hvorpå matematisk viden etableres og valideres gennem bevisførelse såvel som bevisers begrænsninger”.
- “[E]n kvalitativ og intuitiv forståelse af mange af de store idéer inden for matematikken, herunder mønstre, symmetri, bevis, paradoks, rekursion, tilfældighed, kaos, uendelighed osv.”.
til: GYMNASIER
emne: Matematikforestillinger (Beliefs)
UDGIVET: 2024
Forfatter
Maria Kirstine Østergaard
Postdoc
DPU, Aarhus Universitet
Uffe Thomas Jankvist
Professor
DPU, Aarhus Universitet
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Referencer
- Brousseau, G. (1997). Theory of Didactical Situations in Mathematics. Kluwer.
- Ernest, P. (2015). The social outcomes of learning mathematics: Standard, unintended or visionary? International Journal of Education in Mathematics, Science and Technology, 3(3), 187–192.
- Green, T. F. (1971). The activities of teaching. McGraw-Hill.
- Grouws, D. A. (1996). Student conceptions of mathematics: A comparison of mathematically talented students and typical high school algebra students [Paper]. Annual Meeting of the American Educational Research Association, New York, NY.
- Jankvist, U. T. (2015). Changing students' images of "mathematics as a discipline". Journal of Mathematical Behavior, 38, 41–56. doi.orgdoi.org/10.1016/j.jmathb.2015.02.002
- Op’t Eynde, P., de Corte, E., & Verschaffel, L. (2002). Framing students' mathematics-related beliefs. A quest for conceptual clarity and a comprehensive categorization. I G. C. Leder, E. Pehkonen, & G. Törner (red.), Belief: A hidden variable in mathematics education? (s. 13–38). Kluwer. doi.orgdoi.org/10.1007/0-306-47958-3_2
- Pajares, M. F. (1992). Teachers' beliefs and educational research: Cleaning up a messy construct. Review of Educational Research, 62(3), 307–332. doi.orgdoi.org/10.3102/00346543062003307
- Philipp, R. A. (2007). Mathematics teachers' beliefs and affect. I F. K. Lester & D. A. Grouws (red.), Second handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics (Vol. 1, s. 257–315). Information Age.
- Rolka, K., & Roesken-Winter, B. (2015). Networking theories to understand beliefs and their crucial role in mathematics education. I B. Pepin & B. Roesken-Winter (red.), From beliefs to dynamic affect systems in mathematics education: Exploring a mosaic of relationships and interactions (s. 73–93). Springer. https://doi.org/10.1007/978-3-319-06808-4_4
- Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. I D. A. Grouws (red.), Handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics. (s. 334–370). Macmillan. doi.orgdoi.org/10.1177/002205741619600202
- Yackel E. & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27, s. 458-477. https://doi.org/10.5951/jresematheduc.27.4.0458
- Østergaard, M. K. (2022). Middle school students’ beliefs about mathematics as a discipline. [Doctoral dissertation, Aarhus University]. Aarhus University. http://dx.doi.org/10.7146/aul.462