Matematisk kommunikation og sprogbrug

At lære matematik handler om tilegnelsen af et matematisk sprog og om at udvikle matematiske begreber. Læs om, hvad forskningen siger om udviklingen af matematiske begreber, og se forslag til matematiske samtaler med børn i vuggestue og børnehave.

Ida (4 år) og Kenneth (3,5 år) sidder og leger med nogle dukker i børnehaven. Ida har fire dukker, som hun leger med, mens Kenneth har tre dukker, som han leger med. Pædagogen observerer dette og begynder at lege sammen med dem. Efter en stund spørger pædagogen de to børn om, hvem af dem som har flest dukker, og hvem af dem som har færrest dukker. Dette er Ida og Kenneth usikre på, da de ikke har så mange erfaringer med ordene 'flest' og 'færrest'.

At lære matematik er at tilegne sig det matematiske sprog

Når vi i dagligdagen italesætter vores erfaringer og omgivelser ved hjælp af matematik, kaldes det at 'matematisere'. (Kilde 1 og 2)

Vi bruger altså matematiske ord og begreber for at kommunikere de matematiske sider ved vores omverden og aktiviteter. I den indledende fortælling ser vi, at pædagogen forsøger at matematisere børnenes leg med dukkerne ved at spørge dem om, hvem som har færrest, og hvem som har flest. Det ser ud som om, børnene ikke ved det, fordi de ikke kender de matematikholdige ord, som pædagogen bruger.

På mange måder kan man sige, at det at lære sig matematik er at lære et sprog. Et sprog, som indeholder matematiske ord og begreber for at kunne sætte ord på erfaringer, idéer og handlinger. Sprog og tanke er derfor uløseligt knyttet sammen.(Kilde 3)

For at et barn kan udvikle sine (matematiske) idéer, må barnet også udvikle et (matematisk) sprog for det. Al matematiklæring handler derfor om at tilegne sig et matematisk sprog og tilhørende idéer. Denne tilegnelse foregår, når børn er i samspil med andre børn og voksne. Når vi skriver sprog her, tænker vi på sprog i bred forstand: mundtlige og skriftlige sprogudtryk, kropssprog såsom blik, fagter og bevægelser og brug af konkrete materialer. Børn anvender alle disse former for sprogbrug, når de udtrykker sig. De snakker, de tegner og skriver og bruger fingertælling, de fremlægger et givent antal klodser og forskellige geometriske former. (Kilde 4)

Læring af matematiske begreber

Alle begreber har en indholdsside og en udtryksside, som er uløselig knyttet sammen. Begrebsindhold udgøres af alle de tanker, idéer og meninger, som et barn har tilegnet sig gennem sine erfaringer. Begrebsudtryk udgøres af de sprogudtryk, barnet benytter sig af for at kommunikere tanker, idéer og meninger. (Kilde 3)

For eksempel kan et barn på fem år udtrykke sine erfaringer og idéer (det vil sige sit begrebsindhold), om begrebet 'fem' ved at:

• vise fem fingre på en hånd
• skrive talsymbolet 5 eller fem tællestreger
• skrive ordet 'fem'
• vise symbolet for fem ved hjælp af en spilleterning
• lægge fem klodser frem.

Dette eksempel illustrerer også, at der naturligt nok er individuelle forskelle i, hvilke begrebsindhold og begrebsudtryk børn og voksne har tilegnet sig.

Sprogudtryk af 1. orden og 2. orden

For at beskrive hvordan vi mennesker lærer, skelner forskningen mellem det der kaldes for tilegnelse af spontane og videnskabelige begreber, og det, at vi mennesker lærer disse begreber på forskellige måder. (Kilde 3)

Norsk forskning har bygget videre på dette og udledt, hvad der kaldes sprogudtryk af 1. orden og sprogudtryk af 2. orden. (Kilde 4)

• Tilegnelsen af sprogudtryk af 1. orden er fortolket som tilegnelse af spontane begreber. Sprogudtryk af 1. orden er udtryk, som vi bruger spontant og kommunikerer med, det vil sige de sprogformer, vi bruger for at kommunikere det meningsindhold, vi ønsker at få frem.  
• Tilegnelsen af sprogudtryk af 2. orden svarer til tilegnelse af videnskabelige begreber. Sprogudtryk af 2. orden (jf. videnskabelige begreber) er udtryk, som ikke er naturlige for os at bruge. Det er sprogudtryk, vi ikke umiddelbart forstår. Derfor er alle nye ting, som et barn skal lære, på et givent tidspunkt et sprogudtryk af 2. orden. 

Det er derfor forskelligt fra person til person, hvad der på et givent tidspunkt vil være et sprogudtryk af 1. orden, og hvad der vil være et sprogudtryk af 2. orden.

Begrebslæring bliver således den proces, barnet må igennem for at omdanne 2. ordens sprogudtryk til 1. ordens sprogudtryk. (Kilde 4)

Hvis vi i børnehaven ønsker, at børnene skal få erfaringer med nogle af vores talsymboler, fx 6, 7, 8, 9 og 10, og vi antager, at børnene ikke kender disse fra før, vil disse talsymboler da være at betragte som 2. ordens sprogudtryk for børnene, (men 1. ordens sprogudtryk for pædagogen!). Pædagogen må derfor komme børnene i møde og støtte dem i processen med at omdanne disse 2. ordens sprogudtryk til 1. ordens sprogudtryk. Dette gøres gennem et oversættelsesled. (Kilde 4)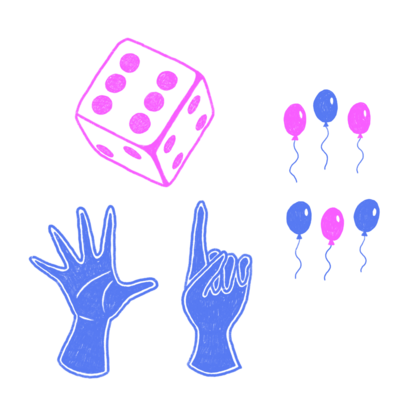 

Pædagogen oversætter mellem sprogudtrykkene, fx gennem at vise, at talsymbolet 6 symboliserer det samme antal som seks fingre, ved at:

• vise seks fingre
• lægge seks klodser frem
• sige, at en myre har seks ben
• vise en sekser på en terning.

Oversættelsesleddet består altså af de sprogudtryk, pædagogen bruger for at anskueliggøre sammenhængen mellem de forskellige sprogudtryk. Sprogudtrykkene, som pædagogen bruger, må alle være af 1. orden, altså sprogudtryk, som barnet umiddelbart forstår. Flere skridt kan være nødvendige i denne oversættelsesproces.Det at oversætte mellem sprogudtryk af 2. orden og sprogudtryk af 1. orden er specielt vigtigt i matematik, fordi matematiske begreber er abstrakte. De skal konkretiseres og eksemplificeres for børnene. Derfor må pædagogen i sit arbejde 'hele tiden' have fokus på denne oversættelse med børnene ved fx, som illustrationen viser, at oversætte antallet af øjne på terningen med talordet 'seks', et antal balloner med talordet 'seks' eller også talsymbolet 6, osv.

Udvikling af matematiske begreber

At skabe matematisk opmærksomhed hos børn i børnehaven handler også om at introducere matematiske ord og begreber ved at sætte fokus på de matematiske sider ved børnenes leg og hverdagsaktiviteter. Det kan fx ske ved, at pædagogen giver børnene erfaringer med talordene: 'en, to, tre, fire' osv og med antalsord: 'mange, få, nogen, færre, flere, flest' osv.

Læs også tema om At tælle.

Børn kommer videre i deres matematiske udvikling ved at akkumulere de matematiske erfaringer, de gør sig. Matematiklæring handler derfor om at tilegne sig begrebsindhold og begrebsudtryk knyttet til de matematiske begreber, som er relevante for børnehavebørn. Denne læringsproces stopper ikke, men fortsætter hele livet. Pædagogens opgave bliver dermed at gøre børnene opmærksomme på matematikken i deres hverdag og introducere et matematisk sprog, som sætter ord på disse erfaringer.

" Børn, som lærer at sætte ord på og begrunde deres egne matematiske idéer, ræsonnere ved hjælp af deres egne og andres matematiske forklaringer og tilkendegive begrundelser for deres svar, udvikler en dyb forståelse, som er kritisk vigtig for i fremtiden at kunne lykkes i matematik." (Kilde 5 - vores oversættelse)

Den matematiske samtale fokuserer netop på at 'sætte ord på', 'begrunde', 'ræsonnere' og 'forklare'. Det er derfor afgørende, at pædagogen lægger op til, at børnene bliver deltagere i sådanne samtaler i børnehaven.

­Det er klart, at vi her ikke kan give en fuldstændig oversigt over alle de matematiske ord, udtryk og begreber, man benytter sig af i børnehaven. Se eksempler i: Ordene har noget matematisk over sig. Hovedpointen er, at pædagogerne er bevidste om at tage det matematiske sprog i brug i mødet med børnene, i deres leg og hverdagsaktiviteter, fx ved at tale om: Matematik i eventyr.
Derfor snakker vi i flere sammenhænge om at have en matematisk samtale med børnene. Den matematiske samtale er en læringssamtale, hvor intentionen er deltagelse og læring i matematik. Se eksempler på matematiske samtaler i teksten: Leg i matematik og matematik i leg.

Den matematiske samtale sætter gang i undring og refleksion omkring matematiske spørgsmål, begreber og idéer. (Kilde 6 og 7)