At undersøge med tal og antal
At undersøge med tal og antal kan give børn begyndende erfaringer med det, der langt senere formelt kaldes statistik og sandsynlighed. Meget af den forskning, som findes om børn og deres læreprocesser knyttet til statistik, omtaler ældre børn, men der findes også forskning om børn i børnehavealderen. Arbejdet med at undersøge tal og antal på denne måde giver realistiske og forhåbentligt meningsfulde sammenhænge for børnene i at arbejde med tal og antal på en systematisk måde. Børnene bliver involveret i sammenhænge, hvor tælling kan bruges som et værktøj til at løse en (matematisk) udfordring.
For de ældre børn i dagtilbud er der mange muligheder for at undersøge fænomener ved hjælp af tal og antal. Doverborg & Samuelsson (2001) giver et eksempel, hvor børn skal undersøge, hvilke aktiviteter de deltager i i løbet af en uge. Man kan sammen med børnene lave en tabel med en oversigt over de forskellige aktiviteter, børnene har deltaget i i børnehaven i løbet af ugen med en streg ud for hver aktivitet, de har været med til, fx at tegne, sjippe, lege i borgen, lege i byggerummet osv. En tabel kan se sådan ud:
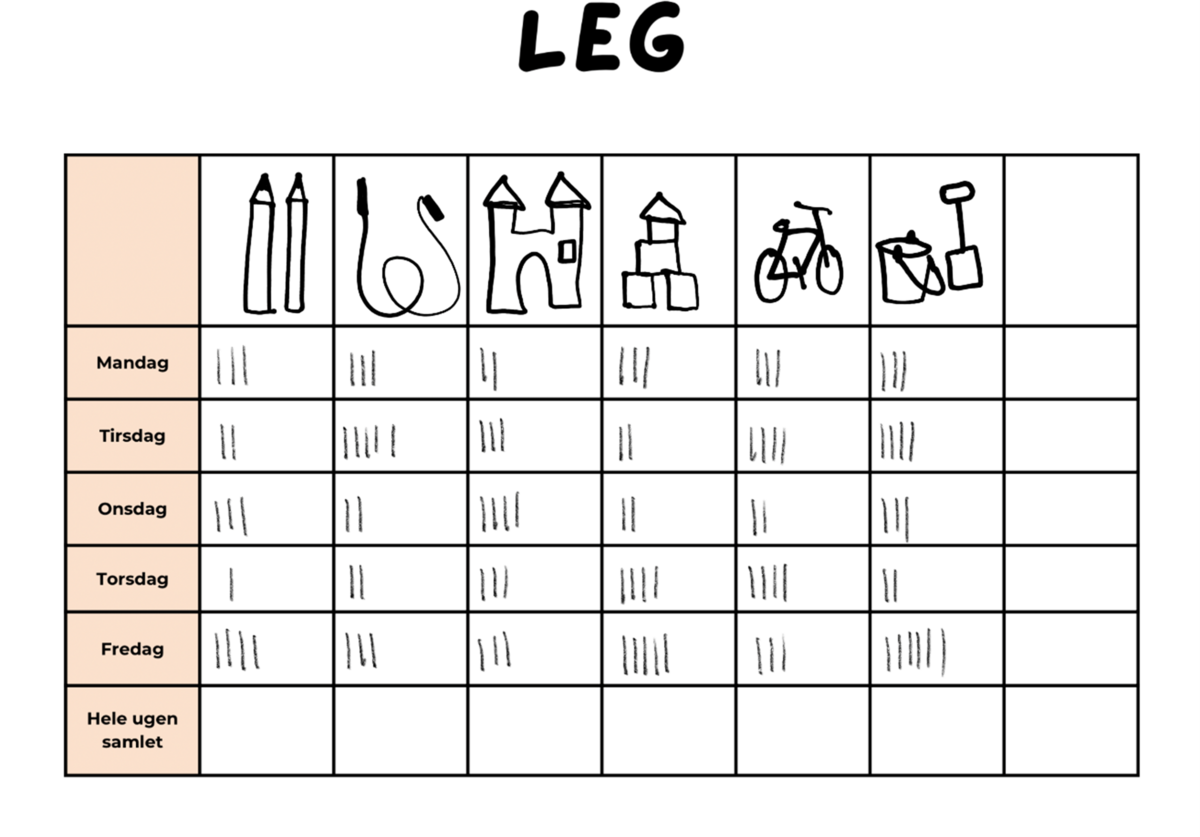
Man kan lave en fælles tabel, eller børnene kan lave hver sin tabel og så sammenligne dem bagefter, når ugen er slut. Dette kan være udgangspunkt for rige matematiske samtaler; samtaler om antallet af streger eller krydser til hver aktivitet, om antallet af forskellige aktiviteter, børnene har været med til sammen osv. I disse samtaler kan man bruge forskellige antalsord og talord som fx få, mange, nogle, færre, tre, fem, to osv. At involvere børn i en sådan aktivitet vil give børnene erfaring med at systematisere. Systematik og det at kunne systematisere er en vigtig kompetence at tilegne sig både generelt og specielt i matematik.
Hvad kræver det af børnene at deltage i sådanne undersøgelser?
Når børn skal foretage undersøgelser med tal og antal, er det en fordel, at de kan tælle – se evt. temaet ‘At tælle’. Der er forskellige principper knyttet til det at tælle, men i denne sammenhæng er det især nyttigt at kunne principperne om stabil ordning, en-til-en-korrespondance og kardinaltalsprincippet. Børnene kan sagtens deltage i undersøgelser med tal og antal, selvom de endnu ikke er sikre på disse principper. Da behøves blot lidt mere støtte fra pædagogen.
- Princippet om stabil ordning handler om, at børn skal lære talordene, og at disse kommer i en bestemt orden eller rækkefølge: en, to, tre, fire, fem osv.
- Princippet om en-til-en-korrespondance handler om, at når man skal tælle en mængde objekter, skal man knytte ét og kun ét talord til hvert objekt, som man skal tælle.
- Kardinaltalsprincippet handler om, at det sidste talord, man siger, når man tæller en mængde objekter, fortæller, hvor mange objekter der er i alt.
Principperne er uddybet i temaet ’At tælle’.
Ud over dette kræves der ingen specielle matematiske erfaringer. Det vil være en fordel, hvis børnene har erfaringer med situationer, hvor man lægger sammen og trækker fra – og her tænkes ikke på erfaringer med at regne plus- og minusstykker. For eksempel får børnene jo erfaring med at lægge sammen, hvis man udfordrer dem til at finde ud af, hvor mange gange alle børnene til sammen har tegnet i løbet af ugen, fx hvis tre børn har tegnet om mandagen, fire børn har tegnet om onsdagen og to børn har tegnet om fredagen, dvs. 9 børn i alt osv. Dette vil børnene også få flere erfaringer med gennem at deltage i denne og andre tilsvarende aktiviteter knyttet til dette tema.
At deltage i aktiviteter knyttet til dette tema vil kunne give børnene rige erfaringer med problemløsning i meningsfulde kontekster; se eksemplerne i teksterne ’At arbejde med tal og antal i praktiske situationer i daginstitutionen’ og ’Forskellige værktøjer, man kan benytte, når børn undersøger ved hjælp af tal og antal’. For et barn er et matematisk problem en opgave eller udfordring, som barnet bliver engageret i og samtidig motiveret til at finde mulig(e) løsning(er) på. Udfordringen eller opgaven må være af en sådan karakter, at barnet ikke umiddelbart ved svaret. Problemløsning er så den proces, som barnet går igennem for at løse et matematisk problem, enten alene eller sammen med andre.
Aktiviteter inden for dette tema vil også kunne skabe udgangspunkt for rige matematiske samtaler, og det giver børnene erfaringer med klassificering (efter egenskaber ved objekterne). Klassificering er det, vi gør, når vi deler fænomener, ting og situationer ind i forskellige kategorier efter bestemte kriterier. Det, som afgør klassificeringen, er de egenskaber, som er fælles, og de egenskaber, som adskiller. I eksemplet med aktiviteter i løbet af en uge klassificerer vi det, børnene laver, som forskellige aktiviteter: tegne, sjippe, lege, bygge osv. Klassificeringen repræsenteres med hver sin kolonne i tabellen ovenfor. Cursio og Folkson (1996) hævder, at hvis bare børnehavebørn får muligheden for det, så er de fuldt ud i stand til at indsamle data, registrere data, illustrere data og diskutere data. Dette viser noget af det potentiale, som arbejdet med at undersøge tal og antal i børnehaven kan have.
Hvad ved vi fra forskningen om børns erfaringer med at undersøge med tal og antal?
Meget af den forskning, som findes om børn og deres læreprocesser på dette område, er foretaget med skolebørn (fx Curcio, 1987; Jones et al., 2000; Makar & Rubin, 2009). Der er dog også nogle studier, der har undersøgt børnehavebørn og deres ræsonnementer og argumentation i forbindelse med at undersøge tal og antal. Friel, Curcio & Bright (2001) argumenterer for, at børn i børnehavealderen kan beskæftige sig med objektdiagrammer, billeddiagrammer og søjlediagrammer. Herunder eksemplificerer vi disse tre diagramtyper.


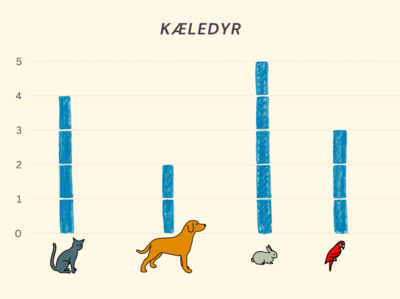
At fremstille og diskutere sådanne diagrammer kan være et udgangspunkt for rige matematiske samtaler. Søjlediagrammet bør have en enhedsinddeling, en streg for hvert objekt, så børnene kan tælle, hvor mange objekter der er i hver kategori.
English (2010) påpeger, at det er vigtigt, at børn tidligt får mulighed for at ræsonnere inden for statistik, da det kan give dem erfaring med en form for modellering. At modellere i matematik vil i store træk sige at løse situationer og problemstillinger fra omverdenen med matematik, fx med tal og diagrammer. Vi kan altså tilrettelægge situationer, hvor børnene møder et matematisk problem, som de skal løse ved at bruge den matematik, de har lært tidligere. Børnene skal også repræsentere matematikken på en måde gennem (hyppigheds)tabeller og diagrammer. Problemer, der kan løses ved hjælp af statistik, fx at kategorisere forskellige blade eller biler og finde ud af, hvor mange blade og biler der er i hver kategori, gør den matematiske udforskning meningsfuld for børnene. Et meget vigtigt element i denne sammenhæng er at tale om og blive enige om kategorierne, og hvilke egenskaber der skal gælde for objekterne inden for samme kategori. Dette kan lede til rige matematiske samtaler, hvilket det gjorde i Englishs (2010) studie.
Til overvejelse i teamet
- Hvordan kan I ellers involvere børnene i undersøgelser af tal og antal?
- Kan I komme frem til andre aktiviteter, I laver med børnene, som giver dem erfaringer med at være systematiske?
- Samtal om, hvordan børnene kan få erfaringer med tælling i aktiviteter knyttet til at undersøge tal og antal.
til: DAGTILBUD
emne: TAL OG ANTAL
UDGIVET: 2024
Forfatter
Martin Carlsen
Professor
Institutt for matematiske fag, UiA
Illustrationer og foto
Mette Bjerre
Adjunkt, ph.d.
Program for matematik- og naturfagsdidaktik, VIA University College
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Curcio, F. R. (1987). Comprehension of mathematical relationships expressed in graphs. Journal for research in mathematics education, 18(5), 382–393.
- Cursio, F. R., & Folkson, S. (1996). Exploring data: Kindergarten children do it their way. Teaching Children Mathematics, 2(6), 382-385.
- Doverborg, E., & Samuelsson, I. P. (2001). Små barn i matematikkens verden. Oslo: Pedagogisk forum.
- English, L. D. (2010). Young children’s early modelling with data. Mathematics Education Research Journal, 22(2), 24-47.
- Friel, S. M., Curcio, F. R., & Bright, G. W. (2001). Making sense of graphs: Critical factors influencing comprehension and instructional implications. Journal for Research in Mathematics Education, 32(2), 124-158.
- Jones, G. A., Thornton, C. A., Langrall, C. W., Mooney, E. S., Perry, B., & Putt, I. J. (2000). A framework for characterizing children's statistical thinking. Mathematical Thinking and Learning, 2(4), 269–307.
- Makar, K., & Rubin, A. (2009). A framework for thinking about informal statistical inference. Statistics Education Research Journal, 8(1), 82–105.