At arbejde med tal og antal i praktiske situationer i daginstitutionen

I den nederste række skulle børnene i samarbejde med hinanden selv finde ud af, hvor mange af hver frugt og grøntsag de tilsammen havde med i løbet af ugen. Børnene gjorde dette på forskellige måder. Nogle satte igen lige så mange tællestreger, som der var i kolonnen over. Andre viste antallet af frugter og grøntsager ved at tegne øjental på terninger (fx øjentallene 5, 5 og 3 eller 6, 6 og 1 for antallet 13), og nogle skrev talsymboler som fx 13. Undervejs talte pædagogen med børnene om, hvad de lavede, og om hvad deres valgte repræsentationer for antallet stod for. Sådanne samtaler kan fx tage udgangspunkt i spørgsmål som: Hvordan fandt I ud af, hvor mange streger der var tilsammen i løbet af ugen? Hvorfor valgte du at tegne øjental på en terning, Mette? Når Eva skriver de to tal, 1 og 3, forstår I så, hvad det betyder? Hvordan kan vi vise antallet otte på forskellige måder? Hvordan vil det se ud, hvis vi bruger øjental i stedet for tællestreger, når vi skal vise antallet af appelsiner i alt?

Aktiviteten kaldet ’Hvad man laver på en uge?’ blev gennemført på tilsvarende vis. Børnene brugte en tabel til at lave en oversigt over forskellige aktiviteter, som de deltog i i børnehaven i løbet af en uge. De tegnede et kryds eller en streg for hver aktivitet, de havde været med til, fx at tegne, at sjippe, at lege i borgen, at lege i puderummet, at cykle og at lege i sandkassen. Børnene lavede hver sin tabel, og så sammenlignede de dem bagefter, da ugen var omme. Dette kom der rige, matematiske samtaler ud af; samtaler om antal krydser eller streger, de havde for hver aktivitet, om antallet af forskellige aktiviteter, børnene havde deltaget i tilsammen osv. I disse samtaler blev forskellige antalsord og talord brugt, fx få, mange, nogen, færre, tre, fem, to osv. Læs mere om, hvor vigtigt det er at bruge det matematiske sprog og sætte ord på erfaringer, som børnene gør sig i teksten ’Matematisk kommunikation og sprogbrug’.

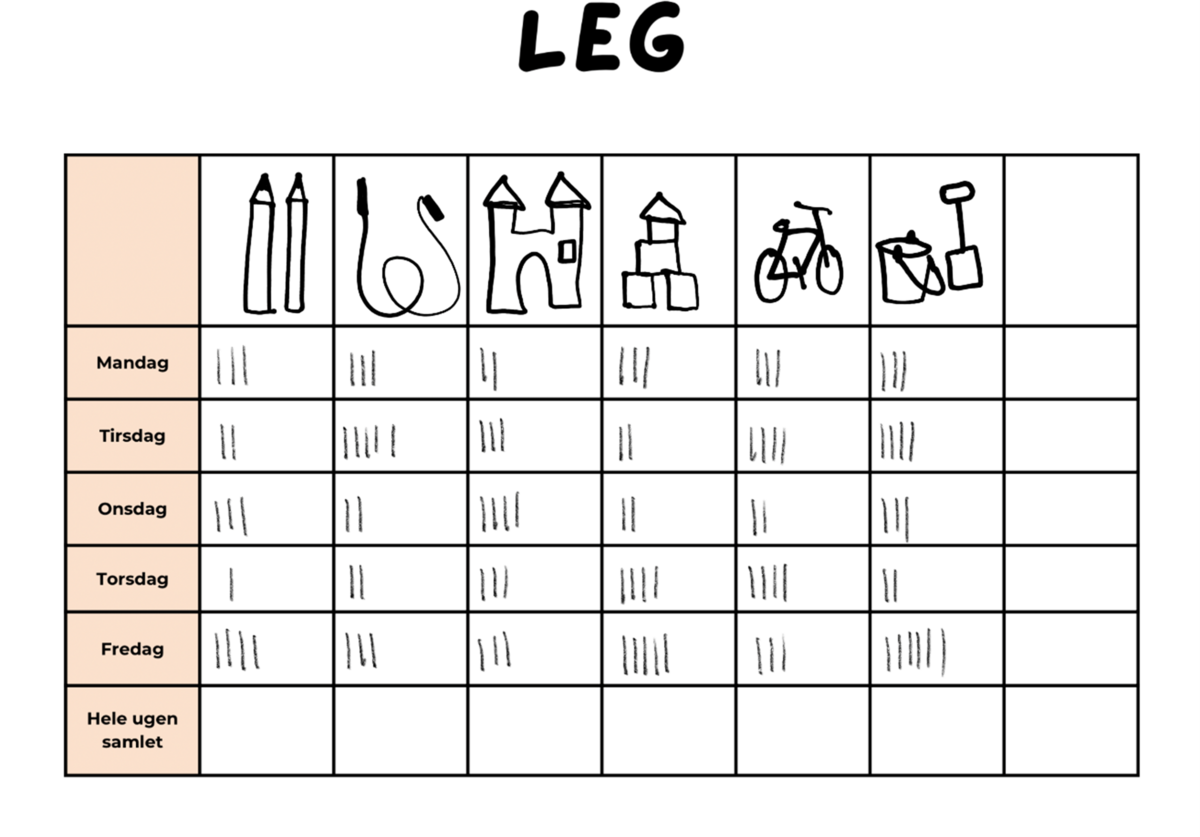
2 – ’At lave og teste terninger’

Doverborg & Samuelsson (2001) beskriver også aktiviteten ‘At lave og teste terninger’. Til denne aktivitet kan man fint bruge almindelige terninger, man har købt, men i eksemplet her lavede børnene selv terningerne af ler. Nogle blev malet sorte med røde prikker, mens andre blev malet røde med sorte prikker. Efter at have lavet terningerne blev børnene interesserede i, hvilke terninger der var ’de bedste’, dvs. fx hvilke terninger der oftest viste seks, når de kastede dem. Hvert barn, som deltog i aktiviteterne, kastede en terning 50 gange (børnene fik hjælp af en voksen til at tælle et så stort antal!). Antallet af kast blev markeret i en tabel. Som i eksemplerne med frugter og grøntsager og aktiviteter i løbet af en uge blev disse tabeller udgangspunkt for rige matematiske samtaler om antal af hvert kast, forskelle mellem antal, hvilket kast som forekom oftest osv. Helt konkrete spørgsmål kunne være: Hvilket øjental fik I flest gange? Hvilket øjental fik I færrest gange? Er der nogen øjental, I fik mange gange? Hvor mange seksere fik I i alt? Hvor mange femmere/enere/treere fik I i alt? Hvor mange flere seksere fik I end femmere? Det er godt også at stille børnene spørgsmål, der drejer sig om, at de skal forklare hinanden, hvordan de fandt ud af svarene på de foregående spørgsmål. Inspirer også gerne børnene til at stille hinanden forskellige matematiske spørgsmål. Det kan fx ske gennem en rolleleg som ’Nyhederne’, hvor et barn interviewer et andet barn om de undersøgelser, de har lavet, og de svar, de har fundet.

Som pædagog kan man også tage en samtale med børnene om forskellen mellem kast, som forekom mange gange, og kast, som forekom få gange, og at dette kan have noget at gøre med, hvordan terningerne blev lavet. Hvis de i stedet for havde brugt terninger købt i en butik, var resultatet måske blevet et andet.

3 – ’At klappe sit navn’

I forbindelse med aktiviteten ’At klappe sit navn’ fortæller Doverborg & Samuelsson (2001), at børnene først skulle klappe lige så mange gange, som der var stavelser i deres navn. De måtte altså lytte sig frem til antal klap, hvilket består i en en-til-en-korrespondance med antal stavelser i navnet – altså ét klap for hver stavelse. Børnene fik så til opgave at tage én duploklods for hver stavelse, de havde i deres navn. Børnene måtte igen benytte princippet om en-til-en-korrespondance, så de tog lige så mange klodser som antallet af stavelser i deres navn. Børnene kunne også kontrollere, at antal klodser, antal klap og antal stavelser var ens ved at benytte kardinaltalsprincippet (at det sidste talord, man siger, når man tæller en mængde objekter, fortæller, hvor mange objekter der er i alt) og finde ud af, om antallet var én, to, tre eller fire. Børnene blev så bedt om at samle deres klodser og bygge et tårn af dem foran sig, så de kunne tale om, at tårnene har forskellige længder på samme måde, som navnene har forskellige længder.

Det viste sig, at børnene byggede tårnene på forskellige måder. Der var fx tre børn, der alle havde tre stavelser i deres navn, som byggede tre forskellige tårne: Det ene barn byggede et tårn med tre klodser. Et andet barn byggede en slags pyramide med to klodser på bunden og den tredje klods på toppen. Et tredje barn lagde klodserne ved siden af hinanden og byggede således ikke noget tårn. Denne situation skabte et udgangspunkt for en samtale mellem børnene og pædagogen om, hvordan én og samme mængde kan deles op og sættes sammen på forskellige måder. Pædagogen gennemførte også en samtale med børnene, hvor de diskuterede, hvordan de kunne koble antallet af klodser med de forskellige talsymboler for antallene én, to, tre og fire, altså 1, 2, 3 og 4.

Pædagogen lod så børnene med samme antal stavelser i deres navn tage én duploklods hver med samme farve. De børn, som havde én stavelse i deres navnet, skulle fx tage en rød klods; de børn, som havde to stavelser i deres navn, skulle tage en blå klods osv. Til sidst satte de klodserne med ens farve sammen til tårn. Pædagogen og børnene talte så om, hvad det kunne betyde, fx at tårnet med blå klodser var noget højere end tårnet med røde klodser. Den matematiske samtale imellem dem indeholdt også diskussioner vedrørende, hvor mange flere klodser der var i det højeste tårn, de havde bygget, sammenlignet med det laveste; hvor mange klodser der var i det næstlaveste tårnet osv. Gennem denne aktivitet fik de deltagende børn erfaringer med princippet om en-til-en-korrespondance og kardinaltalsprincippet (at det sidste talord, man siger, når man tæller en mængde objekter, fortæller, hvor mange objekter der er i alt), og at talsymboler og antal hænger sammen. De fik også erfaringer med at bruge antalsord som flere, flest, færre og færrest og grundlæggende erfaringer med det at lægge sammen og trække fra. Tårnet af klodser i den sidste del af aktiviteten gav børnene erfaringer med en form for fysisk søjlediagram (se teksten ‘Forskellige værktøjer, man kan benytte, når børn undersøger ved hjælp af tal og antal’).