Praksis – At anvende tal og måling

Her vises, hvordan læringssporet kan realiseres i praksis. Der er konkrete eksempler på, hvordan aktiviteterne i de fire faser kan iscenesættes og udføres. Det fremhæves, hvilke faglige pointer det er centralt at behandle undervejs og i opsamlingen, og hvordan man som lærer kan støtte elevernes fælles læring i klassen med sigte på sporets læringsmål.

Læringssporet er designet til 4 til 6 timers undervisning. Det kan placeres i begyndelsen af matematikkurset, da hovedvægten er lagt på at lære en arbejdsmetode (modellering) med matematisk stof hentet fra grundskolen (måling og deling/division).

Det faglige udgangspunkt

Matematiske begreber

De matematiske begreber i ’stakitinddeling’ er kendte fra grundskolen: måling og opmærkning, enheder, multiplikation og division. Med dette udgangspunkt lærer eleverne i problemet med stakitinddeling elementer fra målbeskrivelsen for faget på niveau F, f.eks. at ’anvende tal og symboler, der repræsenterer kendte forhold, samt enkle formeludtryk i deres grundform’.

Matematiske kompetencer

Læringssporet bygger på kompetencerne modellering og problemløsning, som eleverne har mødt i grundskolen. Det nye for eleverne er, at det nu foregår i en erhvervsfaglig kontekst med konkrete materialer, og at der er et direkte anvendelsesperspektiv.

Etablering af fænomenet og det bagvedliggende problem

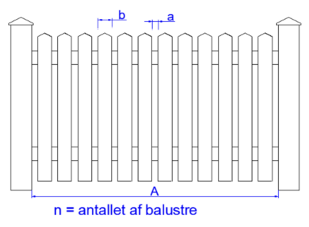
På en tur rundt på skolens område kan læreren fremvise eksempler på inddelinger. Det kan være gelænderet på balkoner, tremmer over lyskasser, sprosser i vinduer osv. Sammen får klassen identificeret problemet: 'Hvordan mon de gjorde, så der er lige meget luft mellem tremmerne?'. Eleverne skal erkende, at problemet kan løses gennem svaret på de to arbejdsspørgsmål: 

• Hvordan fordeler jeg n antal balustre/sprosser/stakitstave med lige meget luft imellem? 
• Hvordan placerer jeg balustre, så der højst/mindst er en ønsket afstand mellem balustrene?

På turen rundt på skolen opbygger eleverne et ordforråd for de enkelte elementer: 'Hedder det stave, pinde, balustre, tremmer? Luft, afstand, felter?'. Og de identificerer og beskriver det generelle fænomen, at der altid er 1 mellemrum mere, end der er balustre. Læreren kan arbejde med sprogliggørelsen af fænomenet med spørgsmål som: 'Gælder det altid at…? Gælder det også hvis…?'.

Den første matematiske modellering fra en fysisk model af problemet

I denne fase skal eleverne udvikle og beskrive en metode til løsning af inddelingsproblemet, og de skal ud fra en fysisk model beskrive modulmålet som baluster + afstand.

Det første skridt fra det konkrete problem på vej mod en generel løsning er at arbejde med fysiske modeller for problemstillingen. Mock-up'en bruges som abstraktionsmateriale ved at være forskelligt fra en reel stakit-opgave på en byggeplads. I klassen arbejder man med mock-up for at bevare forbindelsen til den ægte situation, men samtidig bevare muligheden for at eksperimentere, lave fejl reflektere og lave det om. En mock-up kan laves i træ, eller man kan bruge en lidt mere abstrakt model med papirark der skal fordeles jævnt langs en bordkant.

De to arbejdsspørgsmål, der blev identificeret på rundturen, er ikke lige nemme at løse, og løsningen af det ene kan bruges som afsæt for det andet.

Fælles læring

I fase 3 har eleverne arbejdet med at opbygge en generel forståelse for deres metode til at løse et konkret problem. En måde at rodfæste denne forståelse er ved at sammenligne og udvikle sin egen metode i dialog med de metoder, som andre på holdet har udviklet. Lad eleverne fremlægge, forklare, afprøve, diskutere og sammenligne forskellige metoder og forståelser.

En anden måde at ’trykprøve’ eller udvikle elevernes forståelse er ved at løse tilsvarende problemer. Det kan dels omfatte variationer inden for elevernes erhvervsfaglighed: Inddeling af vinduessprosser, inddeling på skrå trappegelændere i stedet for vandrette, læsning og fremstilling af arbejdstegninger el.lign.

Men læreren kan også inddrage kontekster uden for elevernes erhvervsfaglighed: Nye maskiner, tilsvarende problemer i andre fagligheder osv. Det vil styrke elevernes forståelse for det generelle i matematikken og give dem erfaring med at løse problemer i nye kontekster. Man kalder arbejdet med at sammenligne og variere for ’vandret matematisering’. Det kan man læse mere om i afsnittet Grundlag.

En af de andre metoder, eleverne kan sammenligne deres nyvundne forståelse med, er fagenes udviklede standardmetoder, og målet med undervisningen er da også, at eleverne i slutningen af forløbet har så robust en forståelse, at det kognitive gab til fagets standarder er så lille som muligt. Hensigten er, at eleverne bevarer meningen med aktiviteterne og kan se sammenhængen mellem lærerens (fagets) og deres egen metode.

Hvis ikke eleverne kommer frem til det på egen hånd, må læreren præsentere en ny – og effektiv – metode. Tricket er: Læg bredden af en baluster til afstanden mellem stolperne. Med denne metode får man et helt antal moduler – dog ét modul mere end der er brug for. Denne målte afstand divideres med modulet ’baluster + afstand’. Hvis ikke det går op, rundes op eller ned, og der divideres igen.

Men hvordan kan eleverne opdage dette trick?
En vej derhen kan være, at nogen kan det i forvejen. Det vil jo være synd at negligere, at det for nogle elever findes som eksisterende viden. Hvis ingen elever kender tricket, må man selv forsøge sig med, at få eleverne til at foreslå, at det kan være nemmere at arbejde med hele moduler. Se også sidste afsnit 'Opmærkning/Det smarte greb' i denne fase. Lige så snart idéen er på bordet, handler undervisningen om, at eleverne forklarer og argumenterer for anvendelsen. På basis af en udført handling laves beskrivelser, forklaringer og anvisninger – både sprogligt og grafisk – og evt. med en diskussion af, hvorfor det virker og hvornår.

'Den generelle anvisning' kan have varierende grader af formalisering, men vil nok bestå af følgende algoritme:

1. Beregn $A+b$ (formel symbolsk model), eller 'hold en baluster op ved en stolpe, og mål den plus afstanden mellem stolperne' (sproglig model af realistisk, uformel situation).
2. Beregn 'idealmodulet': den målte balusterbredde ($b$) plus det ønskede mellemrum ($a$).
3. Del afstanden ($A+b$) med 'idealmodulet' ($a+b$) = antal 'idealmoduler' plus 1. Vi lagde jo en ekstra baluster til, fordi der er et mellemrum ekstra og for at kunne regne i moduler.
4. Hvis ikke det går op, skal man enten runde op eller ned. Det afhænger af opgaven, og om afstanden ønskes større eller mindre end $a$.
5. Den afrundede værdi angiver antallet af moduler plus 1 og antallet af mellemrum.
6. Divider afstanden ($A+b$) med antallet af moduler plus 1.
7. Det giver den nye bredde af modulet.
8. Mærk det op kant-til-kant.

Denne anvisning er stadig en sproglig model for det konkrete problem, men den er generel, fordi den skal gælde for en hel kategori af tilsvarende problemer. Tricket med 'ét ekstra modul' dukker også op i ligningerne i fase 4. 

Generalisering: Virker det altid?

Arbejdet med at formulere en general anvisning – som fx vist i punktform ovenfor – kombineret med færdighed i at kunne udføre en stillet opgave vil være et rigeligt og tilstrækkeligt mål for mange elever på erhvervsuddannelserne. Formel notation med symboler er tilføjet de 'gode forklaringer' som støtte til den matematisk velfunderede lærer og kan evt. bruges som supplement til de elever, der kan have gavn af sådanne udfordringer.

I den sidste fase øger man abstraktionsgraden ved at koble symboler på handlinger og sammenhænge. Målet er, at eleverne meningsfuldt forstår symbolerne – både som et udtryk for de handlinger og forklaringer, som de har fortrolighed med, og som et matematisk udtryk for alle tilsvarende sammenhænge, som handlingerne er et enkelt eksempel på. Symbolernes værdi som repræsentation består i, at vi aftaler at $n$ betyder antallet af balustre uanset hvor mange balustre. Og det er underforstået at $n$ skal være et positivt heltal. Undervejs i omformninger af udtryk behøver man ikke bekymre sig om symbolernes betydning. Det er først til slut, når man igen kobler udtryk til den virkelige problemstilling, at symbolerne får en konkret betydning.

For mange elever er det en udfordring at læse en mening ind i formler og bogstavudtryk. Opgaven er her at tolke de symbolske udtryk ved hjælp af forståelsen og begreberne fra det konkrete problem – og den anden vej at udtrykke begreberne og metoderne fra problemløsningen ved hjælp af symboler og regneudtryk.

Det kan for eksempel gøres, ved at eleverne i grupper får til opgave at opstille forskellige udtryk for at beskrive afstanden mellem stolperne, $A$, hvor man samtidig lægger vægt på, at eleverne skal forklare, hvad de enkelte led står for. Det ligger ud over målene for matematikken på niveau F, at eleverne lærer at omforme algebraiske udtryk, men hvis læreren viser forskellige algebraiske udtryk på tavlen, kan eleverne deltage ved at forklare, hvordan tal og symboler kan repræsentere kendte forhold. Det er vigtigt, at eleverne får mulighed for at tillægge symbolerne mening.

Opdagelsen fra fase 1 'mellem stolperne er der altid er et mellemrum mere, end der er antal balustre' kan fx skrives på symbolform som '$n$ balustre og $n+1$ mellemrum', og så er man allerede godt på vej til at skrive afstanden mellem stolperne med symboler:

$A = n \cdot b + (n +1) \cdot a$

Klassen fællesgør forståelsen af, at $n \cdot b$ betyder 'den samlede bredde af de $n$ balustre', og ($n+1$) repræsenterer antallet af mellemrum, mens a betegner længden af mellemrummet, dvs. afstanden mellem balustrene. Det er altså et længdemål, som er angivet i f.eks. millimeter. Afstanden mellem stolperne kan også forklares ved, at der til hver baluster hører en afstand, og derudover er der en ekstra afstand. Så afstanden mellem stolperne kan også skrives som: 

$A = n \cdot (a+b) + a = n \cdot m + a$

Det kan med ord forklares som, at 'afstanden mellem stolperne er $n$ moduler gange modulstørrelsen ($a+b$) plus et ekstra mellemrum'. Her har man indført symbolet $m$ for bredden af et modul ($a+b$). Det kan give anledning til en snak om, at når man forklarer afstanden på to forskellige måder, svarer det til en omformning af den tilhørende formel.

Denne øvelse er for at lære (og træne), at matematiske handlinger – som at tælle op og sammenligne antal – kan udtrykkes som symboler og regneudtryk. Man kan fortolke sådanne regneudtryk, i dette tilfælde en formel, som en matematisk handling eller en sammenhæng, der kan udtrykkes med ord.

Det første inddelingsproblem, 'Hvor meget afstand har jeg mellem balustrene, hvis jeg skal fordele n balustre ligeligt mellem stolperne?', kan skrives som

$a = \frac{A - n \cdot b}{n + 1}$

og f.eks. forklares som 'Afstanden mellem balustrene finder man ved at trække alle balustrene fra $A$ og dividere resultatet med antallet af mellemrum ($n+1$). Der er jo netop 1 mellemrum mere end antal balustre, $n$'. Igen svarer formuleringen til en omformning af formlen.

Det næste inddelingsproblem er: 'Der må højst være $a$ afstand mellem balustrene' eller 'Der skal mindst være $a$ afstand mellem balustrene'. Hvor mange balustre skal der så bruges, og hvad er den nye afstand mellem balustrene?

Dette problem kan løses ved et smart greb! Vi har jo fastlagt, at der skal være en afstand mere end antallet af balustre, så derfor lægges en baluster til afstanden $A$ mellem stolperne, for så er der lige mange afstande $a$ som balustre $b$. En baluster og et mellemrum kan opfattes som et modul, og længden af et sådant modul giver vi symbolet $m$. Der tages altså udgangspunkt i afstanden $A + b$. Denne afstand divideres med 'idealmodulets' længde $m$, som er balusterbredden plus største/mindste acceptable afstand $a$.

$A + b = (n+1)(a+b)$

$(n+1) = \frac{A+b}{a+b} = \frac{A+b}{m}$

Her er det nødvendigt at træde ud af matematikkens verden af symboler og beregninger og tolke resultatet i forhold til opgaven.

1. Hvad er det, jeg har fundet ud af med min beregning?
2. Giver det mening, at resultatet bliver et decimaltal?

Resultatet er et antal – og antallet er ét modul mere end det nødvendige antal balustre. Derfor skal jeg bruge et heltal. Resultatet af divisionen giver ikke nødvendigvis et heltal; altså må man afrunde.

Antallet af moduler er nu ændret, altså må modulbredden også have ændret sig. Det fordrer en ny udregning: Hvad er den nye modulbredde?

Den kan opskrives som:

$\frac{\text{Afstand}+\text{baluster}}{\text{antal moduler}} = \text{den nye modulbredde}$

Eller med symboler

$\frac{A+b}{n_m}= m = (a+b)$

Der er to formål med denne øvelse. Den ene er, at det kan give eleverne en erkendelse af, at bogstaver repræsenterer noget konkret, dvs. for at læse mening ind i symbolformen. Det andet mål er, at de oplever, at løsningen på problemet 'stakitinddeling' ikke er en endelig formel, men en kombination af at måle, tælle, beregne og en afrunding op eller ned.

Gennem en snak i klassen ser eleverne, at man kan beskrive meningen i de enkelte symboludtryk med de samme hverdagsbegreber, og eleverne oplever, at der er en sammenhæng mellem de forskellige formler. Denne tilgang opfylder målet for matematik på F niveau 'at give eleven eller lærlingen grundlag for videre uddannelse'.

Der kan også formuleres åbne opgaver fra de oplysninger, man kan finde på forskellige hjemmesider. Her er nogle eksempler: