Grundlag – At anvende tal og måling

Det teoretiske grundlag for læringssporet består af matematikdidaktisk forskning inden for felterne (1) instruerende vs. konstruerende læring, (2) modellering, (3) brugen af konkrete materialer og (4) sproget i matematikundervisningen.

(1) Instruerende versus konstruerende læring

En vigtig forskel på matematik i folkeskolen og i erhvervsuddannelserne er forholdet til verden uden for skolen. Det er en klassisk udfordring både for elever og lærere i folkeskolen, når eleverne spørger 'Hvad skal jeg bruge det til?'. Der mangler kontekst og dermed mening (Hansen, 2019).

På erhvervsuddannelserne har man ikke det problem. Meningen og anvendelsen er til stede overalt og hele tiden, og de fleste elever er meget motiverede for at lære at løse problemer hurtigt og effektivt. Der kan så opstå det modsatte problem i matematiktimerne: Lærerne kommer til udelukkende at støtte erhvervsuddannelsernes primære formål – at uddanne problemløsere. Det giver sig udtryk i en stærk instruerende tilgang til undervisningen: Læreren demonstrerer en metode og eleverne opøver færdighed i metoden. I bedste fald får eleverne lejlighed til at efterprøve metoden i konkrete situationer og får feedback på deres forståelse i 'dialogen' med slutproduktet.

En undervisning baseret på færdige algoritmer, der formidles og øves, er baseret på et ønske om effektivitet og hurtighed. Dette kræver rutine. Denne tilgang har sin berettigelse i et fag, der er præget af gentagne arbejdsgange, der giver mulighed for rutine. I en faglighed baseret på en tradition med sidemandsoplæring, hvor mester og svend viser, hvad der virker, og lærlingen imiterer og øver sig, er det nærliggende at anvende denne tilgang og værdier i matematikundervisningen. 

En anden tilgang er den konstruerende. Eleverne opbygger gradvis deres egen forståelse ved en tiltagende abstraktion fra det konkrete problem til en generel forståelse af metoden (Carpenter, T.P., & Lehrer, R., 1999).

I et arbejdsmarked, der er præget af nye arbejdsgange, redskaber, problemer og opgaver, er det ikke altid tilstrækkeligt at opnå rutine. Der er det nødvendigt at være fleksibel og kunne genskabe, tilpasse og overføre metoder. Begge tilgange har deres berettigelse.

En konstruerende tilgang til algebra består af to elementer: matematisering og generalisering. De forstås her som handlinger. Det vil sige, at algebra i denne sammenhæng forstås som en proces; en måde at behandle problemer på.

Generaliseringen gennemgår forskellige forståelsesniveauer på vej mod en generel formel matematik. I en konstruktivistisk tilgang er der en særlig opmærksomhed på, at eleverne bruger deres egne konstruktioner og forklaringer. Disse forklaringer kan tage to former: modeller af realistiske uformelle situationer, f.eks. udmøntet i at eleven beskriver og forklarer sine egne handlinger, og modeller for generel formel matematik, som f.eks. udmønter sig i, at eleven giver en anvisning på, hvordan problemet kan løses generelt med ukendte størrelser.

(2) Modellering

Det er velbeskrevet i matematikdidaktisk forskning, at matematisk modellering kan være et didaktisk middel til at motivere elevers matematiklæring og til at styrke deres begrebsforståelse (Blomhøj, 2019). Derfor lægges der i læringssporet op til at arbejde med modellering af fænomener og problemstillinger, som eleverne kender til og kan forstå, eller som de kan tage til sig og gøre sig erfaringer med i undervisningen og i erhvervsfaglig praksis (Lesh & Harel, 2003). Tilgangen bygger især på RME, der står for Realistic Mathematics Education (for en generel introduktion se Bull & Blankholm, (2022)). Her tager man udgangspunkt i et realistisk, eventuelt autentisk problem, som eleverne kan gøre sig konkrete erfaringer med, og som de kan undersøge gennem konkrete handlinger. Det giver grundlag for, at eleverne gennem gradvis matematisering kan udvikle en model af det konkrete problem. Gennem fortsat matematisering, hvor man bl.a. anvender algebra, kan de konkrete modeller udvikles til modeller for, hvordan man kan forstå og løse problemerne generelt. Det er igennem denne proces, at eleverne vha. modellen opnår forståelse for den involverede matematik. I RME udpeger man fire niveauer af aktiviteter, som gennemløbes i en proces, der kaldes emergerende (i.e ”som dukker op”) modellering. De er indarbejdet i dette læringsspor og beskrives kort her (Gravemeijer, 2007):

 1. Konkret aktivitet i sammenhæng med den foreliggende opgave. Her hviler fortolkningen og løsningen af opgaven på forståelsen af, hvordan man skal handle i den konkrete kontekst. Et eksempel kan være en beregning af afstanden mellem to balustre ud fra mock-up’en uden indførelse af symboler. Dette er beskrevet først i fase 2 i praksis.

2. Henvisningsaktivitet. Den første matematiske model, som eleverne opstiller, er en model af den konkrete situation, og den refererer til aktiviteter og handlinger, eleverne har foretaget. Et eksempel på en model-af en konkrete situation, som er etableret i undervisningen, er udtrykkene med symboler til beregning af antal balustre og afstanden mellem dem som beskrevet i fase 2 i praksis.

3. Generel aktivitet, hvor modellen med dens konkrete referencer optræder som model-for en generel matematisk sammenhæng. Det er der eksempler på i fase 3 i praksis, hvor der opstilles generelle modeller til beregning af mellemrummene mellem balustrene, og som kan benyttes i mange andre kontekster.

4. Formel matematisk aktivitet, hvor fortolkning og forståelse af matematikken ikke længere kræver støtte fra konkrete situationer, der tjener som model for den matematiske sammenhæng. Det er vist i fase 4 i praksis. I en erhvervsuddannelsesmæssig sammenhæng er det op til diskussion, hvor langt man vil gå i retning af en sådan formel matematisk aktivitet.

De forskellige niveauer anvender forskellige repræsentationer. Hvor det første niveau typisk ikke vil anvende symbolsprog, er dette den dominerende repræsentationsform på det formelle niveau. På niveauerne imellem anvender man forskellige repræsentationer. Det kan være konkrete repræsentationer, diagrammer, tegninger, talt eller skrevet sprog, der sammen med en begyndende brug af symboler bruges til at udvikle algebraisk tænkning. Dette læringsspor viser et eksempel på, at det talte sprog sammen med konkrete repræsentationer kan ’bære’ en matematisering og generalisering af et praktisk problem til en generel metode.

På de forskellige niveauer kan der også foregå en ’vandret matematisering’, dvs. en bearbejdning af det matematiske udtryk, uden at man skifter op eller ned i abstraktion. Det kan f.eks. være, når læreren får eleverne til at sammenligne deres mundtlige forklaringer, når eleverne udvikler tegninger af problemet, eller når de prøver metoden af med smallere balustre eller en ændret afstand mellem stolperne. Ændring af et algebraisk udtryk for f.eks. at isolere n er også vandret matematisering.

Hensigten med vandret matematisering er, at eleverne får en bredere funderet forståelse.

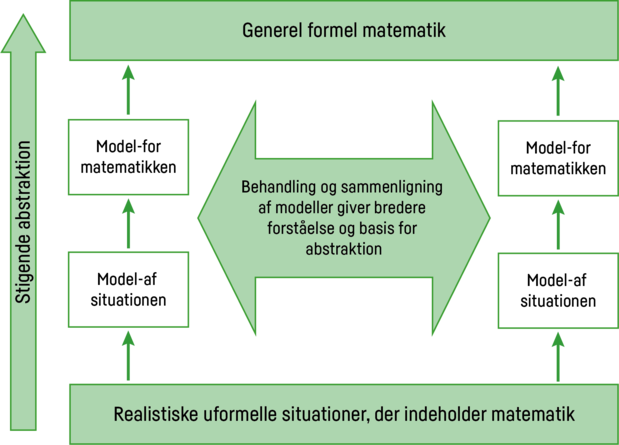
Figuren viser den emergerende modelleringsproces. Eleverne tager udgangspunkt i en realistisk situation eller et konkret problem. Gennem gradvis stigende abstraktion udvikler de formel matematik – eller de opnår en bredere funderet forståelse på det enkelte abstraktionsniveau ved at variere og sammenligne deres forståelser. De enkelte faser i læringssporet er bygget op over progressionen i matematiseringen.                     

(3) Sproget i matematikundervisningen

Sprog er samtale mellem mennesker. At sætte ord på sine tanker er med til at fastholde og udvikle dem – skrivning gør det endnu strammere. Sprog kan også opfattes som en bro til at danne relationer mellem repræsentationer; så ved at udvikle sprog og bruge sprog kan man blive mere sofistikeret i sin beherskelse af matematikkens repræsentationer og kompetent i at kunne oversætte mellem repræsentationer.

Ud over de sædvanlige repræsentationer – grafer, diagrammer og symboler – kan repræsentationer i matematik også være f.eks. konkrete materialer. Det kan både være materialer, der kommer direkte fra fagenes praksis, f.eks. brædder, fliser og mursten, og semi-didaktiserede materialer, f.eks. den mock-up af et stakit, der indgår i dette læringsspor. En situation, en handling, en fortælling eller en forklaring kan også repræsentere en matematisk sammenhæng eller et begreb (Eriksen, 2000).

Læreren kan i sin undervisning udvikle og understøtte sproglig udvikling ved f.eks. at indgå i dialog, formulere nye problemstillinger eller andre måder at betragte problemet på, stille åbne spørgsmål og give plads til elevernes spørgsmål og (mis)forståelser. God undervisning skal give eleverne mulighed for at benytte forskellige indgangsvinkler, at stille nye spørgsmål undervejs, at diskutere mulige måder at løse opgaven på og at præsentere resultater på selvstændig måde.

Åbne opgaver giver mulighed for flere tilgange, og det fordrer sprog for at skabe forbindelser. En særlig udfordring i dialogen er at være opmærksom på synsvinkel og indholdsperspektiver: Taler vi om det samme? Har vi fælles forståelse?

I arbejdet med at udtrykke sin forståelse skaber eleven mening i matematikken, og i dialogen skaber parterne en fælles forståelse mellem deres individuelle forståelser (Eriksen, 2000).  

(4) Brugen af konkrete materialer

Tone Dalvang (2006) deler brugen af konkrete materialer op i 4 trin af abstraktion:

• Det mest konkrete: Hverdagsting, der repræsenterer sig selv.
• Halvkonkret: En tegning eller en model af en ting.
• Halvabstrakt: Tingene repræsenteres i en anden og mere forenklet form, f.eks. tællestreger, diagrammer og klodser. Disse 'ikoniske' repræsentationer holder gradvist op med at ’ligne’ den konkrete ting og er i stedet udtryk for, hvad vi har ’aftalt’, at de skal repræsentere.
• Abstrakt form: Matematiske repræsentationer, symboler og formler.

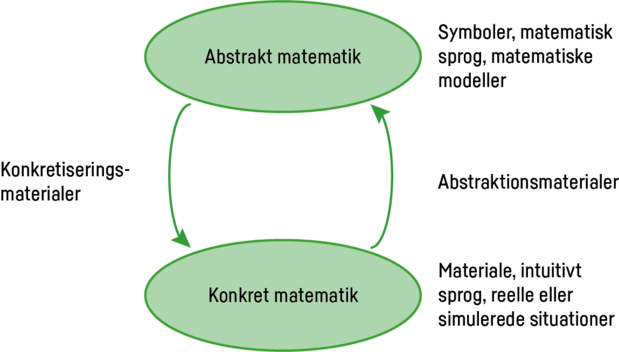
Elise Klaveness (2010) skelner mellem konkretiseringsmaterialer og abstraktionsmaterialer. Det samme materiale kan være begge dele, afhængig af om intention med det er at konkretisere noget abstrakt eller abstrahere noget konkret. Det er vigtigt, at eleverne lærer at relatere det konkrete arbejde til abstrakt matematik.