At anvende tal og måling
Introduktion
Dette læringsspor er eksemplarisk for en matematikundervisning, der tager udgangspunkt i et konkret problem, og som kan løses med en erhvervsfaglig anerkendt metode. I læringssporet vises et eksempel på, hvordan eleverne selv kan nå frem til en metode gennem en undersøgende tilgang. Eleverne kan herved opleve, at de ved brug af matematik og især algebra kan forstå grundlaget for en erhvervsfaglig metode.
En erfaren håndværker kan udvikle robuste og fleksible metoder til at løse opgaver, der minder om hinanden. En algebraisk tilgang til at udvikle disse metoder har den styrke, at forståelsen for generelle sammenhænge kan udvikles på kortere tid end gennem erfaring. Algebra er universelt, så det kan bruges i mange forskellige erhvervsfaglige sammenhæng og i mange uddannelser.
I erhvervsfaglig praksis er det vigtigt, at eleverne kan fagets standardmetoder effektivt og sikkert. Hvis de skal kunne anvende metoderne fleksibelt og i nye situationer, er det imidlertid nødvendigt, at deres færdigheder er baseret på forståelse af, hvorfor metoden virker. Det kræver forståelse af de indgående matematiske begreber og operationer, der så til gengæld også kan anvendes i mange andre situationer. Didaktisk giver det derfor god mening, at matematiklæreren venter med at demonstrere den effektive, praktiske løsning på problemet, til eleverne selv har arbejdet med at forstå og løse problemet ved hjælp af matematik.
Her benyttes problemet ’stakitinddeling’ som eksemplarisk for en problemløsningsproces, hvor eleverne guides til algebraisk tænkning ved at tage udgangspunkt i en gradvis stigende abstraktion og generalisering i en trinvis modelleringsproces.
Den faglige standardmetode til at opmåle og inddele stakitter, gelændere, fliselægning, placering af vinduesfag m.v. introduceres senere i læringssporet.
Læringsspor til Erhvervsuddannelserne udviklet af NCUM under den fælles indsats for tal og algebra.
Udgivet 2025
Forfattere på læringssporet er Mikkel Johansen, Charlotte Krog Skott, Morten Blomhøj, Thomas Kaas og Marit Hvalsøe Schou.
Mål
I problemet med ’stakitinddeling’ er der en tæt relation til den faglige praksis og en vekselvirkning mellem denne og matematiske beregninger. Eleverne skal hele tiden vurdere, hvordan et problem eller en handling kan beskrives og behandles med matematik, og hvordan deres beregninger kan omsættes til konkrete handlinger.
Det er ikke tanken, at eleverne skal udvikle en generel formel, men snarere at de kan foretage opmålinger, beregninger, opmærkninger og vurderinger samt tage beslutninger i relation til en praktisk problemstilling, hvor en korrekt løsning bl.a. vurderes af kulturelle normer for æstetik, effektivitet og præcision.
Det matematiske læringsudbytte i arbejdet med problemet består i at anvende matematikken til at gennemføre en modellering af et praktisk problem ’med sikkerhed og overblik’.
Matematisering er at omsætte et problem til matematisk sprog, så man kan anvende matematiske metoder og begreber til at løse problemet.
Målet med læringssporet er dobbelt, nemlig at:
-
eleverne gennem gradvis matematisering af et konkret problem, anvender og forstår en metode, der kan beskrives og løses delvist ved hjælp af algebra, og som derfor kan anvendes på forskellige problemer af samme type.
-
eleverne bliver i stand til effektivt, sikkert og med forståelse at anvende en matematikbaseret fremgangsmåde til løsning af et erhvervsfagligt praktisk problem. Her vist eksemplarisk ved ’stakitinddeling’.
De to mål hænger sammen, og fokus på dem må balanceres gennem forløbet. Udgangspunktet er, at eleverne forstår den erhvervsfaglige problemstilling og accepterer dens praktiske relevans, samt at de oplever, at matematik er nødvendig for at kunne beskrive og forstå problemet præcist og generelt.
Sammenhæng med læreplanen
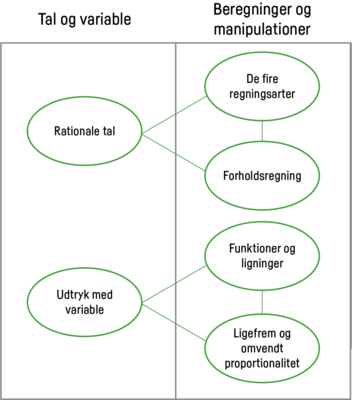
Ifølge bekendtgørelse nr. BEK nr 555 af 27/04/2022 indeholder faget matematik følgende fagområder:
Almindelige regneoperationer med tal og konkrete formeludtryk: Overslagsregning, regningsarternes hierarki, procentregning, forholdsregning (F-niveau). På D-niveau derudover almindelige regneoperationer med tal og symboludtryk, konkrete som abstrakte. På C-niveau desuden regneregler, herunder parenteser og regning med potenser og rødder.
Algebra og funktioner: Løsninger af ligninger af første grad og ligefrem proportionalitet med dertilhørende funktioner og grafisk beskrivelse (F-niveau). Derudover omvendt proportionalitet, løsning af to ligninger med to ubekendte (E-niveau). På C-niveau desuden andengradsfunktioner, eksponentielle funktioner og logaritmefunktioner med tilhørende grafiske afbildninger, regressionsanalyse samt løsning af simple uligheder.
Erhvervsuddannelsernes kernestof inden for tal og algebra er fordelt på niveauerne F, E, D og C. Fagområder, der berøres i dette læringsspor, er illustreret i figuren nedenfor.
Målet er, at eleverne oplever, at matematik er et effektivt redskab til at løse praktiske problemer, og at de gennem konkrete anvendelser kan få mening med matematikken og forståelse for den erhvervsfaglige metode.