Tilgang – At løse ligninger
I afsnittet beskrives den fagdidaktiske viden, der anvendes i læringssporet, for at støtte elevernes læring. Det drejer sig for det første om forskellige typer af ligninger og forskellige måder at opfatte en ligning på. For det andet omfatter det forskellige strategier og metoder, som eleverne kan bruge til at løse ligningerne med. For det tredje beskrives udfordringer ved brugen af de repræsentationer (modeller), som man benytter til at løse ligninger med. Og endelig for det fjerde omfatter det andre vanskeligheder, som elever oplever ved opstilling og løsning af ligninger.
Først beskrives denne viden overordnet og dernæst vises, hvordan den indgår i hver af læringssporets fire faser (se Oversigten). Afsnittet afsluttes med nogle bemærkninger om, hvordan arbejdet med løsning af lineære ligninger kan føre til andre matematiske områder, der behandles i gymnasiet.
Der er grundlæggende to retninger i læringssporet. Det ene er at fastholde og uddybe elevernes forståelse af ligninger i konkrete situationer i deres nye hverdag på gymnasiet. Her vil også andre fag kunne byde ind med situationer, der kræver, at eleverne selv kan opstille ligninger fra en given kontekst, og at de derefter kan løse dem. Den anden er at introducere den symbolske ligningsløsning, som for eksempel benyttes ved bevisførelse og i andre matematiske ræsonnementer.
Der er flere grunde til, at ligningsløsning også er vigtigt i gymnasiet, selvom matematikprogrammer i mange situationer overtager de beregninger og symbolmanipulationer, som eleverne tidligere selv måtte foretage. Brugen af matematikprogrammer kan være motiverende, fordi man får mulighed for at modellere autentiske og komplicerede hverdagssituationer, men samtidig er der en risiko for, at eleverne mister både færdigheder og forståelse for den ligningsløsning, der er nødvendig for at følge og forstå matematiske ræsonementer og beviser. Eleverne har derfor brug for et robust grundlæggende ligningsbegreb for at kunne håndtere de krav, der stilles i gymnasiets matematikundervisning.
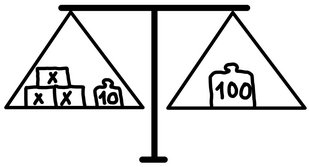
Den måde, man griber en ligning an på, afhænger i høj grad af, hvordan man opfatter den. Tager man en simpel ligning som $3x + 10 = 100$, vil nogle elever opfatte det som en betingelse, der skal være opfyldt, og hvor man må prøve sig frem, indtil man finder den rigtige værdi for x. Andre elever vil se en gammeldags vægt for sig (se billedet til højre). På den ene side har man placeret 3 ens lodder med ukendt vægt og et 10 kg lod (som vist på Figur 1). På den anden side står et 100 kg lod. Man skal altså finde ud af, hvilken vægt loddet med ukendt vægt har. Her har vi en ligevægtssituation. Man kan også tænke på ligningen som en beregning eller en funktionsmaskine: gang med 3, læg 10 til, og så skal det give 100. x kan findes ved at regne baglæns. Nogle elever vil se en sammenhæng mellem det hele, som er 100, og de enkelte dele, der består af 3 dele med en værdi, vi ikke kender endnu, og en del, som har værdien 10. Endelig vil mange elever se en relation mellem nogle tal inklusiv et ukendt x, nogle operationer og et lighedstegn. Med denne forståelse er strategien at lægge det samme til eller trække det samme fra på begge sider, gange eller dividere med det samme på begge sider og til slut ende med et udtryk ”$x = \dotsc$". Man benytter så at sige en standardalgoritme, der i den didaktiske litteratur til grundskolen kaldes fjern og isulér (ordet fjern hænger sammen med den rent fysiske fjernelse af konkrete materialer på begge sider af ”lighedstegnet”, som man gør i de indledende stadier i ligningsløsning i grundskolen). På gymnasiet omdøber man det til reducer og isolér, og her omfatter ordet reducer både det at ”gøre det samme på begge sider” og at omskrive på begge sider af lighedstegnet.
For at forstå, hvad en elev gør med en given ligning, er det altså nødvendigt at afkode, hvordan eleven ser ligningen, og selvom eleven ikke behandler ligningen, som man forventer (eller ønsker), er det ikke nødvendigvis en forkert strategi, som eleven har valgt. For eksempel kan ”gæt og tjek”-strategien føre til et bedre gæt næste gang, hvis eleven tænker over sammenhængen mellem det tal, han har sat ind, og det resultat, som kommer ud. Brugen af matematikprogrammer og numeriske og grafiske metoder til løsning af ligninger gør at ”gæt-tjek-bedre gæt” og ”aflæs og tjek” er vigtige strategier.
Ikke alle ligninger kan opfattes på de måder, som er beskrevet ovenfor. Det betyder, at ikke alle løsningsmetoder er til rådighed for eleverne. Vi ser derfor på, hvilke typer lineære ligninger man kommer ud for i gymnasiet, og hvordan de kan løses.
Forskellige typer ligninger og deres løsning
Ligninger opdeles i aritmetiske og ikke-aritmetiske ligninger. I de aritmetiske ligninger forekommer den ubekendte kun på den ene side af lighedstegnet, og for at løse dem kan man ”regne baglæns”. Et eksempel er $3(x + 4) + 2 = 29$. Her skal man finde det tal, som når man først lægger 4 til, dernæst ganger summen med 3 og lægger 2 til, så får man 29. Det betyder, at man får 27, når man ganger summen med 3, men så må summen af x og 4 være 9, og dermed må x være 5. Nogle elever har glæde af at se metoden stillet op som et diagram, som siden kan udvides til at løse fx eksponentielle ligninger (se Grundlag). Eleven skal derefter oversætte diagrammet til formel ligningsløsning som vist på Figur 2.
ㅤ

ㅤ
Med algebraisk notation kan diagrammet oversættes til:
$\begin{align*}
3(x + 4) + 2 &=29\\
3(x+4) &= 27 \quad & & \text{”det omvendte af at lægge 2 til er at trække 2 fra”}\\
x+4 &= 9 \quad & & \text{”det omvendte af at gange med 3 er at dividere med 3”}\\
x &= 5 \quad & & \text{”det omvendte af at lægge 4 til er at trække 4 fra”}\\
\end{align*}$
I meget simple aritmetiske ligninger, fx $x + 3 = 5$, har man ikke behov for at operere på den ubekendte. Det har man til gengæld i eksemplet ovenfor, og for nogle elever er det svært – ikke mindst hvis der forekommer negative tal. Disse vanskeligheder er uddybet i afsnittet Grundlag.

Det forholder sig anderledes med de ikke-aritmetiske ligninger, hvor den ubekendte forekommer på begge sider af lighedstegnet som i $3x + 20 = x +164$. Her er det ikke muligt at regne baglæns, for hvad skal man regne på? Man må derfor ty til andre metoder. I nogle tilfælde kan man benytte sig af ligevægtsmodellen som introduktion til metoden ”fjern og isolér”, hvor man ”gør det samme på begge sider (se læringssporet At løse ligninger, hvor man kan finde flere modeller, der anvendes til at arbejde med ligningsløsning i grundskolen). Her kan man opfatte ligningen som en vægt med lige meget på begge sider eller som to tændstiksituationer, hvor der er lige mange tændstikker på hver side (se Figur 3).

Metoden fjern og isolér består af en række omskrivninger af en lineær ligning. Omskrivningerne foretages ved hjælp af fjerne-strategier, og når den sidste omskrevne ligning er på formen $x = t$, hvor $t$ er et tal, er den ubekendte $x$ isoleret, og dens værdi(er) gør ligningen sand (Radford, 2022).
Ved at fjerne eller tilføje det samme på begge sider i modellen (ligningen) kan man få den på aritmetisk form. Der er et stort kognitivt spring fra de aritmetiske til de ikke-aritmetiske ligninger. Det hører sammen med opfattelsen af lighedstegnet. I det første tilfælde opfatter eleven lighedstegnet som en opfordring til at beregne noget. Man kalder det et operationelt syn på lighedstegnet. For at løse en ikke-aritmetisk ligning er man derimod nødt til at kunne se lighedstegnet som en relation mellem to størrelser. Løsningen af ligningen er det tal, der gør, at lighedstegnet gælder. Dette kalder man et relationelt syn. Man kan forklare det kognitive spring ved det, der kaldes proces-objekt-dualiteten, som er velbeskrevet i den didaktiske litteratur og udfoldet i afsnittet Grundlag. En elev med et operationelt syn på lighedstegnet vil altså se lighedstegnet som en proces. For at få et relationelt syn skal det imidlertid opfattes som et objekt, som man kan gøre noget ved – i dette tilfælde omforme til andre ækvivalente ligninger.
Mange ikke-aritmetiske ligninger kan dog ikke fortolkes inden for ligevægtsmodellens rammer; for eksempel når der forekommer negative tal. Sådanne ligninger kaldes algebraiske ligninger. Ved at arbejde med modellen og oversætte mellem model og algebraisk notation er det i mange tilfælde muligt at udvide beregningerne – og dermed slippe modellen – til at omfatte løsning af algebraiske ligninger.
Det vil være de færreste elever i gymnasiet, der har problemer med konkrete aritmetiske ligninger, hvorimod en del elever kan have udfordringer med de øvrige typer. Det er derfor godt at vide, hvilke greb man kan benytte sig af for at støtte eleverne med løsningen af denne type ligninger. I nogle tilfælde kan brugen af forskellige modeller være en hjælp. Man skal dog være opmærksom på, at nogle elever vil have svært ved at forlade modellen igen, og det kan give problemer, når eleven møder andre typer af ligninger. Når man benytter en model som fx ”vægt-modellen” til løsning af præ-algebraiske ligninger (se Grundlag), vil den ubekendte stå for vægten af et objekt, og eleven vil identificere den ubekendte som et positivt tal. Hvis eleven har svært ved at slippe den konkrete model, giver det problemer, når ligningerne indeholder negative tal, som jo ikke giver mening i modellens kontekst. Til gengæld kan modellen være med til, at eleverne ser en ligning som ”to sider, der giver samme værdi, når der indsættes en bestemt værdi for den ubekendte” – frem for den operationelle forståelse af, at her er noget, der skal regnes ud. Det kan bruges til at forankre forståelsen af, at man må operere på hele ligninger som fx ved løsning af to ligninger med to ubekendte.
Brug af forskellige repræsentationer
Inden for den matematikdidaktiske forskning er det velbeskrevet, at brugen af forskellige repræsentationer både kan støtte elevernes forståelse, men også at det kan give anledning til vanskeligheder. I læringssporet bliver der derfor lagt vægt på, at eleverne får mulighed for at arbejde med flere repræsentationer, såsom algebraisk notation, sproglige beskrivelser og grafiske repræsentationer. I mindre udstrækning trækkes der på tegninger af de modeller, som eleverne har mødt i grundskolen, fx ”regne baglæns”-diagrammet, vægt- eller tændstikmodellen.
I nogle tilfælde kan det hjælpe eleverne, at man benytter to repræsentationsformer sammen og samtidig. Eleverne har mødt grafisk ligningsløsning i grundskolen både ved løsning af én ligning og ved løsning af to ligninger med to ubekendte. Denne tilgang fravælges ofte til fordel for rent algebraiske metoder i gymnasiet, men forskningen viser, at mange elever vil drage fordel af at kunne benytte begge metoder, da den grafiske løsning kan støtte, hvis eleven går i stå under omformning af ligningen/ligningerne eller ikke er i stand til at fortolke et symbols resultat (fx ingen løsninger eller uendelig mange løsninger til et ligningssystem). Den grafiske repræsentation kan også anvendes som støtte til at læse ny mening i en ligning. For eksempel kan man af graferne se, for hvilke værdier af den ubekendte at venstre side af en ligning er henholdsvis større eller mindre end højre side. Det giver oplagt mening ved modellering, men er også relevant i en ren matematisk sammenhæng. Den grafiske repræsentation er også effektiv ved diskussion af de mulige typer af løsninger til en lineær ligning.
Løsning af ligningssystemer
Et ligningssystem består af to (eller flere) ligninger med to (eller flere) ubekendte, som skal være opfyldt på samme tid. Det er altså ikke blot ”et par ligninger”, og det er vigtigt at eleverne oplever dette. Man skal derfor være varsom med at præsentere meget simple ligningssystemer, der kan løses ved hjælp af en enkelt variabel, fx "På restauranten blev der serveret tre gange så mange burgere som pizzaer. Tilsammen blev der serveret 212 måltider. Hvor mange pizzaer blev der solgt?".
Det er vigtigt, at eleverne oplever, at ligningssystemet har relevans, og at der ikke er andre måder at løse problemet på. Man kan derfor benytte situationer, der kræver, at der indføres to variable som i dette eksempel:
Eksempel
På et museum koster entréen 280 kr. for en voksen og tre børn. To voksne og to børn skal betale 360 kr.
Hvor meget koster entréen for en voksen? Og for et barn?

Ligningssystemer kan præsenteres på flere måder: som tekstopgaver, hvor ligningerne først skal stilles op; som ligninger uden en kontekst; eller grafisk som et par af rette linjer. Ligningerne for disse rette linjer kan repræsenteres ved ligninger af typen $y = ax + b$ og på normalform $ax + by = c$. Det er vigtigt, at eleverne får mulighed for at arbejde med dem alle, og at de både benytter analytiske og grafiske metoder i løsningen af et ligningssystem og kan sammenligne både metoder og resultater. For eksempel vil nogle elever gå i stå, hvis et ligningssystem ikke giver netop én løsning. Hvis de i stedet løser den grafisk, vil de kunne se, at de to ligninger kan repræsenteres ved parallelle linjer, der eventuelt er sammenfaldne, og at det kan forklare resultatet.
Et andet rent matematisk eksempel, der kan understrege denne pointe, er:
Eksempel
Om to tal kender du deres sum og deres differens. Find tallene. Er der altid netop ét talpar som løsning på en sådan opgave?
Elever med et operationelt syn på lighedstegnet ser tegnet som en opfordring til at udføre en beregning. Elever med et relationelt syn ser lighedstegnet som et udtryk for, at hver af dets sider er ’ens’. (Radford, 2022).
Nogle kendte vanskeligheder i forbindelse med ligninger
I brugen af flere repræsentationsformer skal man være opmærksom på, at overgangen fra én repræsentationsform til en anden kan give anledning til læringsvanskeligheder for nogle elever. Det kan man opleve, når der er behov for at opstille ligninger fra en sproglig beskrivelse – en situation, der både forekommer inden for matematikken selv og på tværs af andre fag. I nogle tilfælde må man også kunne gå den anden vej og fortolke en ligning i en bestemt kontekst. Nogle elever vil i oversættelsen fra en sproglig til en symbolsk repræsentation ”oversætte ord for ord”. Et typisk eksempel er ”elev-lærer”-problemet: "Der er 6 gange så mange elever, som der er lærere på skolen (se Figur 4). Opstil et udtryk, der kan beskrive sammenhængen mellem antallet af elever og antallet af lærere". Nogle elever vil direkte oversætte sætningen ord for ord til $6 \cdot E = L$. Andre elever vil nok kunne forstå problemstillingen sådan, at der er én lærer for hver seks elever, og nogle vil måske endda tegne situationen. Men de vil alligevel ende med udtrykket $6 \cdot E = L$, fordi de 6 E’er fortolkes som et billede af den store gruppe og L’et som billedet af den lille gruppe, og lighedstegnet repræsenterer en sammenhæng mere end en ækvivalens.
Der er en række typiske fejl, som elever laver, når de løser ligninger, og som er velbeskrevet i den matematikdidaktiske litteratur. Her skal nævnes to typiske fejl, som man bør være opmærksom på. Begge fejl optræder i forbindelse med løsningsmetoden reducer og isolér, hvor eleven ”skal gøre det samme på begge sider". Det er den eneste af de løsningsmetoder, der er beskrevet ovenfor, som kan anvendes på alle lineære ligninger, og den anvendes i vid udstrækning på symbolske udtryk i bevisførelse. Derfor er det et mål, at alle elever skal lære denne metode. De to typiske fejl, som beskrives her, har begge med minustegnet at gøre. Den første fejl opstår, når eleverne ikke forbinder minustegnet med det, der står bagefter. Fejlen illustreres bedst med et eksempel:

Man kan se, at eleven ikke opfatter minustegnet som hørende til de $3x$, der står bagefter. Når man så trækker $2x$ fra på begge sider, får man $3x - 2x = 1x$ i stedet for $-3x - 2x = -5x$.
Den anden fejl opstår, når eleven vil have et led til at gå ud og derfor fjerner, dvs. trækker fra på begge sider, men ikke bemærker, at leddene har forskelligt fortegn:

Eksemplet viser, at eleven fra tredje til fjerde linje vil have $5$ til at gå ud og derfor trækker $5$ fra på begge sider. Men leddet var $-5$ på venstre side, og derfor burde eleven have lagt $5$ til på begge sider i stedet.
Det er derfor vigtigt at præsentere eleverne for opgaver, hvor den slags problemer kan opstå, så man kan få diskuteret dem med klassen.
