Tilgang – At forstå brøker

Det er centralt, at eleverne oplever behovet for at beskrive verden gennem brøker. Behovet kan fx opstå gennem arbejdet med heltalsdivision, hvor vi godt kan dele $12$ boller mellem $2$ personer, men skal vi dele $11$ boller mellem $2$ personer, opstår behovet for at kunne beskrive en mængde med brøker. Her har vi brug for en måde at beskrive den mængde, de får hver. I eksemplet fremgår det, at regnearten division er særlig vigtig i forbindelse med brøker, da det er den eneste af de fire regnearter, hvor resultatet skaber behovet for de rationale tal, når vi regner inden for de naturlige tal.

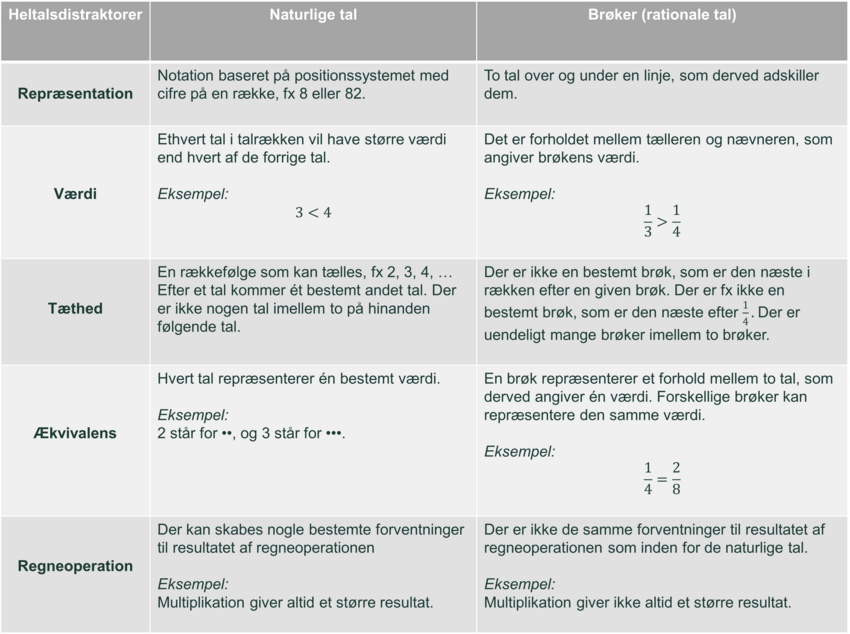
Når en klasse begynder at arbejde med at forstå brøker, er det vigtigt, at dette arbejde tager afsæt i at udvide deres talbegreb fra de naturlige tal til de rationale tal. Denne proces tager tid, og tankegangen kræver abstraktion, da elevernes tidligere erfaringer med de naturlige tal skal udbygges, men også på nogle områder ændres (se Tabel 1). I Tabel 1 vises udvalgte egenskaber ved naturlige tal, som ikke gælder for rationale tal, og som læreren derfor skal være opmærksom på, at eleverne ikke fejlagtigt kommer til at overføre – man taler i den forbindelse om heltalsdistraktorer.

Som det fremgår af Tabel 1, kan elevernes forståelse af de naturlige tal distrahere deres forståelse af brøker, men forståelsen af de naturlige tal er også med til at støtte udviklingen af brøkbegrebet. Det er derfor centralt, at eleverne har opbygget en god og fleksibel talforståelse – herunder forståelse af positionssystemet og en grundlæggende forståelse af regningsarterne (særligt multiplikation og division) inden for de naturlige tal – før arbejdet med at forstå brøker påbegyndes. Særligt har division vist sig at være et vigtigt fundament for arbejdet.

Der er en grundlæggende bevægelse i læringssporet, som går ud på, at eleverne gradvist udvikler de forskellige måder at forstå brøker. I denne bevægelse skal eleverne samtidigt blive opmærksomme på, hvordan brøker opfører sig anderledes end de naturlige tal og derved undgå de forskellige heltalsdistraktorer. Det er en proces, hvor eleverne går fra at have opbygget et talbegreb centreret i de naturlige tal til et talbegreb, der inkluderer de rationale tal.

Gennem læringssporet skal eleverne derfor arbejde med problemorienterede opgaver, der involverer forståelse og brug af brøker i forskellige situationer. Forståelse af brøker er blevet knyttet til fem grundlæggende betydninger. De betegnes som: kvotient, del-helhed, mål, forhold samt operator. Hver af de fem faser har én betydning som omdrejningspunkt, men ofte vil de andre betydninger også kunne komme i spil og støtte elevers udvikling af brøkbegrebet.

I fase 2 arbejdes med betydningen del-helhed. Del-helhed viser sig fx i forbindelse med pizzaslices og lagkagestykker. Hvis vi ser på eksemplet $\frac{3}{4}$, så inddeles 'den hele' i fire lige store dele, og herefter fjernes de tre. Igen bygges der videre på elevernes forståelse af ligedeling, men med særligt fokus på, hvad det vil sige, at delene repræsenterer lige store stykker – altså at $\frac{1}{4}$ og $\frac{2}{8}$ repræsenterer den samme størrelse. 

I fase 2 er der fokus på at undgå, at en klasse udvikler heltalsdistraktoren ’ækvivalens’ (se Tabel 1). Denne distraktor består i, at eleverne overfører deres viden om, at hvert naturligt tal står for en bestemt mængde eller størrelse, fx tre stole eller fire kopper. Inden for de rationale tal kan forskellige brøker imidlertid betegne den samme værdi. Fx angiver $\frac{1}{4}$ den samme størrelse af en kage som $\frac{2}{8}$, hvis altså brøkdelene tages af den samme kage, dvs. helhed. Denne egenskab skyldes, at en brøks værdi bestemmes af forholdet mellem dens tæller og nævner.

I fase 4 arbejdes med betydningen forhold – også kaldet ratio. Forhold er den eneste af de fem betydninger, hvor tæller og nævner ikke referer til en samlet værdi, men hvor tæller og nævner ses som to selvstændige enheder, der forholder sig til hinanden. Når vi på denne måde sammenligner værdien af brøkens tæller med værdien af dens nævner, kaldes det for en forholdsforståelse. $\frac{1}{2}$ kan fx betegne forholdet mellem mængden af havregryn og vand i havregrød. For hver deciliter havregryn skal man bruge $2$ dl vand. Forståelsen af brøker som forhold kan bl.a. bruges til at anslå værdien af brøker. Fx har $\frac{22}{34}$ en værdi, der er tæt på en halv, da nævneren er næsten dobbelt så stor som tælleren. Betydningen forhold eller ratio lægger navn til de rationale tal. Forståelsen består i at opfatte brøker som et forhold mellem to heltal, kaldet henholdsvis tæller og nævner. Hvis brøken har en værdi mindre end $1$, vil det ofte være lettest at anslå dens værdi ved at vurdere, hvor mange gange tælleren kan være i nævneren, eller ved at se på, om tælleren og nævneren består af to tal, der er tæt på hinanden. Brøken $\frac{97}{99}$ repræsenterer fx en værdi tæt på $1$. Modsat vil en stor forskel mellem tæller og nævner, såsom $\frac{2}{99}$, repræsentere en værdi tæt på $0$. Forståelsen af forhold er forbundet med de andre betydninger, særligt del-helhed og kvotient.  

I fase 4 er der særligt fokus på at undgå, at en klasse udvikler heltalsdistraktoren ’værdi’ (se Tabel 1). I fasen skal klassen arbejde med at anslå værdierne af de brøker, de bliver præsenteret for, ved at tage afsæt i en brøk og ud fra symbolerne anslå dens værdi. Det er en forudsætning, at klassen kender brøken som notation fra faserne 1-3.

I fase 5 arbejdes med den sidste betydning, hvor brøker betegner en ’operator’, der kan ændre eller skalere en størrelse. Den anvendte operation er multiplikation.

Eksempel: Der var kun $\frac{3}{4}$ af klassens $24$ elever tilbage. For at gennemføre operationen kan vi først finde $\frac{1}{4}$ af de $24$ elever ved at dividere med $4$ (nævneren) og få $6$. Derefter kan vi finde $\frac{3}{4}$ af de $24$ ved at multiplicere resultatet, altså $6$, med $3$ (tælleren). Vi kan også gøre det omvendte; først multiplicere med $3$ og så dividere med $4$. Stambrøken spiller altså også en central rolle, når en brøk betegner en operator. Klassen skal derfor gennem arbejdet med mål i fase 3 have udviklet en forståelse af, at $\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$ er det samme som $\frac{3}{4}$.

I slutningen af fase 5 kan klassen arbejde med at finde helheden, når de kender delen. Denne del af fasen kan vente til 5. klasse. Det centrale er, at klassen arbejder med at bruge brøken som en operator, der kan bruges til at ændre eller skalere en anden størrelse. I denne fase er den anden størrelse altid et heltal. Denne betydning er central i klassens arbejde med at kunne multiplicere brøker med heltal eller multiplicere to brøker.  

I fasen er der fokus på at undgå heltalsdistraktoren ’regneoperation’ (se Tabel 1). Denne distraktor dækker over, at man ikke kan have de samme forventninger til resultatet af regneoperationer med rationale tal som med naturlige tal. Multiplikation giver fx ikke altid et større resultat inden for de rationale tal.