Praksis – At forstå brøker
I denne del af teksten udfoldes læringssporet med henblik på brug i undervisning. Først omtales de tidsmæssige rammer, som sporet er tænkt indenfor. Derefter beskrives den viden og kunnen hos eleverne, som sporet bygger videre på. Til sidst uddybes hver af de fem faser, som læringssporet består af.
De tidsmæssige rammer
Det vil ofte være passende at begynde læringssporet i starten af 4. klasse, men i nogle klasser vil det give mening at starte i slutningen af 3. klasse. Det centrale er, at eleverne har opbygget en god talforståelse inden for de naturlige tal og har opbygget fleksible regnestrategier; særligt inden for regnearten division. Fase 4 og 5 bør ligge i 5. klasse.
I de fleste klasser vil det være hensigtsmæssigt at lade læringssporet strække sig over flere undervisningsforløb. Det kan fx dreje sig om to forløb á tre uger; evt. i hver sin del af et skoleår. I hvert forløb kan det være en god idé at supplere det faglige indhold med fx lege og spil.
Det faglige udgangspunkt
Forståelse af brøker bygger videre på elevers tidligere erfaringer med de naturlige tal og regning med dem. Det er vigtigt, at elever kan udvikle et sammenhængende talbegreb, hvor brøker bliver en del af deres samlede talforståelse. Selvom de naturlige tal kan distrahere eleverne i deres forståelse af brøker i form af de beskrevne heltalsdisktraktorer, er forståelsen af de naturlige tal også med til at støtte udviklingen af brøkbegrebet. Det er derfor et fokus, at eleverne har et godt fagligt udgangspunkt (som vist i oversigten).
For det første er det en forudsætning, at eleverne har en grundlæggende forståelse af, hvad det vil sige at dele i lige store dele, eller hvad det vil sige, at noget er lige stort. Der vil være elever, som mener, at figurerne i Figur 3 repræsenterer $\frac{1}{3}$, fordi de ikke har den grundlæggende forståelse for betydningen af lige store dele.
For det andet er det en forudsætning, at eleverne har en god forståelse af division med heltal. Eleverne bør bl.a. på forhånd have arbejdet med forskellige opgaver med division, hvor der opstår en såkaldt rest. Det kan fx være $\frac{25}{4}$.
For det tredje er det en forudsætning, at eleverne har en udviklet forståelse for multiplikation, hvilket naturligvis hænger sammen med division. Det er derfor vigtigt, at eleverne er kommet videre i deres forståelse af multiplikation end blot at betragte det som gentagen addition. Det centrale er, at de har en forståelse af, hvad det vil sige, at noget fx er fire gange så stort – eller at kunne skalere noget op og ned, hvor forholdet beholdes. Hvis fx siden i et rektangel bliver dobbelt så stor, skal bredden også være dobbelt så stor, hvis forholdet mellem længden af siderne skal bevares.
Den sidste forudsætning er en grundlæggende forståelse af positionstalsystemet, hvilket vil sige, at elever kan veksle ubesværet mellem $100$’er, $10$’ere og $1$’ere. De skal med andre ord forstå, at cifrenes indbyrdes rækkefølge har betydning: $32$ er ikke det samme som $23$. Derudover anser de ikke værdien af tallet $32$ som $5$, fordi de mener, at $2 + 3$ er lig med $5$. Hvis eleverne ikke har dette udgangspunkt, bør der arbejdes videre med at få opbygget disse forudsætninger, inden eleverne begynder på læringssporet.

Fase 1
Fase 1 kan fx vare omkring 6 lektioner. Fasen går ud på, at eleverne – ud fra deres forskellige forudsætninger – løser problemer med kvotient. Hensigten er, at eleverne begynder at udvikle en forståelse af behovet for de rationale tal igennem arbejdet med at løse forskellige problemer. Det centrale er, at problemerne er knyttet til en kontekst, som anskueliggør behovet for at kunne beskrive en længde eller størrelse med andet end de naturlige tal. Desuden skal problemet være ét, som eleverne let kan forestille sig, og som giver dem rige muligheder for at bruge konkrete materialer eller egne tegninger som støtte.
Fase 1
At løse problemer, der involverer at forstå en brøk som en kvotient. Det vil sige et resultat af en delingssituation – og at kunne sammenligne størrelser.
En tur i zoo
Det gennemgående scenarie i fire af faserne kan fx være en tur i zoo. Læreren sætter scenen gennem en samtale med klassen om, hvad det vil sige at være dyrepasser i zoo. I fase 1 skal dyrepasseren fodre forskellige grupper af aber med æbler. Fordelen ved at bruge billedet af æblet er, at der altid implicit vil være en indikation af, hvad det underliggende hele er.
Et eksempel på et sådant problem:
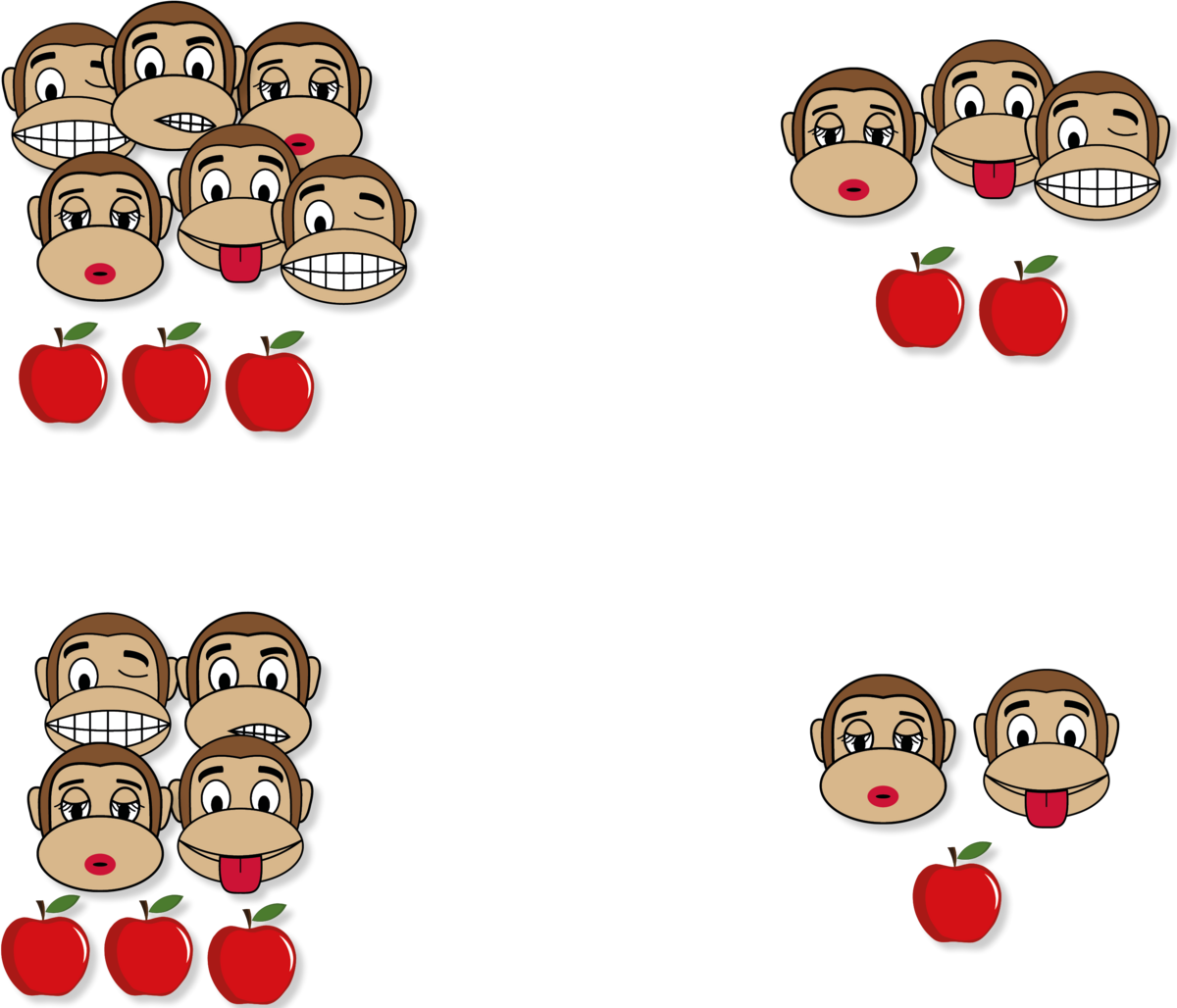
Dyrepasseren i zoo, Oskar, deler æbler ud til grupper af aber. Den første gruppe med 6 aber får 3 æbler, den næste gruppe med 3 aber får 2 æbler, den tredje gruppe med 4 aber får 3 æbler, og den sidste gruppe med 2 aber får 1 æble (se Figur 4). Da han har delt alle æblerne ud, opdager han et ekstra æble i sin pose. Hvilken gruppe af aber skal have det ekstra æble? Hvad vil være mest retfærdigt?
Læreren har illustreret de forskellige grupper med aber og tildelte æbler på tavlen. Det er altså betydningen af en kvotient, der tages afsæt i. Eleverne arbejder herefter på løsninger gennem tegninger og diskussion i grupperne. Herefter samler læreren op på løsningerne og diskuterer dem med klassen. Det må meget gerne gøres gennem de forskellige tegninger, som forskellige grupper har lavet. Hvordan viser vi den mængde æbler, de forskellige aber har fået? Hvordan kan vi inddele æblerne forskelligt (se Figur 5)? Hvilken gruppe skal have det ekstra æble, for at det bliver mest retfærdigt? Hvordan kan vi dele hvert æble op? Lærerne introducerer herefter brøken som en måde at beskrive de forskellige mængder på. Når 3 aber skal dele 2 æbler, får de fx $\frac{2}{3}$ æble hver. Det kan være, at del-helhed naturligt kan blive inddraget i samtalen, når de forskellige tegninger samles.
Vi kan lave en næste runde med klassen, hvor det diskuteres, om der er en bedre fordeling af æblerne. Hvordan skulle dyrepasserne have fordelt æblerne til at begynde med, så det var mere retfærdigt? Hvis vi beholder grupperne? Hvis vi laver grupperne om? Hvordan skriver vi brøker, som betegner den mængde æbler, som hver abe kan få? Vi kan evt. samle arbejdet op ved at gå modsat og skrive brøken $\frac{2}{5}$ på tavlen og bede eleverne tegne eller fortælle en historie, som passer til denne brøk.
Det centrale er bl.a. at give eleverne mulighed for at erfare, at når nævneren bliver større, bliver den mængde, brøken angiver, mindre.

Fase 2
I fase 2, der strækker sig over ca. 6 lektioner, skal eleverne arbejde med betydningn del-helhed som en måde at forstå det forhold, brøken beskriver. Særligt er der fokus på at skabe erfaringer med ækvivalente brøker $\frac{1}{2}=\frac{2}{4}$. Altså at $\frac{1}{2}$ repræsenterer den samme værdi som $\frac{2}{4}$, det vil sige det konstante forhold mellem tæller og nævner – med andre ord at arbejde med at forstå begreberne ”forlænge” og ”forkorte”. De danske navne på de to begreber kan forvirre forståelsen, idet det lyder som om, at brøken bliver kortere eller længere i processen.
Forståelsen af ækvivalens er central, når der skal opbygges et solidt brøkbegreb, der sikrer, at eleverne (senere) kan oparbejde fleksible strategier i regningen af brøker. Fx er den forståelse central, når vi arbejder med at finde fællesnævner, eller når vi skal omskrive til brøk til procent, fx $\frac{1}{2}=\frac{50}{100}=50\%$.
Fase 2
At forstå brøker som en del af en helhed med særligt fokus på ækvivalente brøker (brøker er ækvivalente, hvis de repræsenterer den samme størrelse, fx $\frac{4}{8}=\frac{1}{2}$).
Slangerne i zoo
Et eksempel på et sådant problem er følgende opgave, der viderefører scenariet fra zoologisk have:
Den zoologiske have har en særlig art slanger, som er grønne og sorte. Slangerne i zoo skifter nogle gange ham, men denne sjældne art skifter ikke bare ham, den skrifter også til et nyt mønster, da den synes, det er sjovest. Reglen for alle mønstre er, at slangen altid er lige så sort og grøn som før, selvom mønsteret er nyt.
Læreren sætter en 'slangestrimmel' på $48$ cm op på tavlen. Den ene halvdel af strimlen er farvet grøn, og den anden er farvet sort. En 'slangestrimmel' kan laves af en kassebon eller af noget andet papir. Bredden kan fx være $8$ cm (alternativt kan man lave slangestrimlerne om til $36$ cm eller $24$ cm og bredden mellem $4$ og $8$ cm).
Klassen starter med en samtale om, hvor stor en del af slangen der er grøn, og hvor stor en del der er sort. Herefter viser læreren en ny slange, der er inddelt i fjerdedele, hvor hver anden er sort og grøn. Samtalen fortsætter: Hvor stor en del af slangen er nu farvet grøn? Sort? Hvordan kan vi skrive det? Er slangen mere eller mindre grøn, hvis vi sammenligner med den ovenover?
Eleverne placeres i grupper med slangestrimler på $48$ cm. De bliver bedt om at lave et nyt slangemønster, så slangen er halv sort og halvt grøn.
Der samles op på tavlen, hvor alle slanger hænges op. Hvordan ved vi, at de er halvt grønne? Hvordan har grupperne lavet mønsteret?
Det centrale er herefter, at de forskellige brøkdele skrives og tælles, så fx $\frac{1}{16}+\frac{1}{16}+\cdots+\frac{1}{16}=\frac{8}{16}$ skrives op med samme systematik som $\frac{1}{4}+\frac{1}{4}=\frac{2}{4}$.
Aktiviteten kan her fortsætte individuelt med slanger på $24$ cm. Hvordan kan vi lave nye mønstre, hvor halvdelen er farvet grøn? (Husk at skrive en brøk i hvert af de farvede felter)
Opsamlende samtale på tavlen. Er de store slanger og de små slanger lige grønne? Eller er den store mest grøn?
Aktiviteten kan evt. fortsætte med andre benspænd, såsom at $\frac{1}{4}$ af slangen er grøn, $\frac{1}{4}$ gul og $\frac{1}{2}$ blå. Eller med krav om, at der skal være felter, som udgør $\frac{1}{12}$ af slangen.
Det væsentlige er samtalen: Hvornår fylder de farvede felter lige meget? Hvorfor er alle slangerne lige grønne? Hvordan kan det være, at $\frac{1}{2}$ er det samme som $\frac{2}{4}$? Og $\frac{3}{6}$? Hvordan kan vi se det på brøken? Kan vi finde på andre?
Herefter arbejdes der i sporet videre med andre brøker som fx $\frac{1}{3}, \frac{2}{6}, \frac{3}{9}$.
Det vigtige er bl.a. at give eleverne mulighed for at:
- opdage det konstante forhold mellem tæller og nævner, når vi arbejder med ækvivalente brøker.
- opbygge en begyndende forståelse af at forkorte og forlænge en brøk.


Fase 3
Fase 3 kan fx vare to uger (8 lektioner). Fasen tager afsæt i, at eleverne – ud fra deres forskellige forudsætninger – løser problemer med at måle ved brug af stambrøker (der er en tæt sammenhæng til del-helhed, hvor vi sammenligner delen med helheden). Det vigtige er, at der skabes en situation, hvor stambrøken bruges som en enhed til at måle med, hvorefter brøker sættes ind som længder på tallinjen (altså længden fra 0) for til sidst at betragte brøken som et punkt på tallinjen. Elevers brug af tallinjen inden for brøker kræver, at de videreudvikler deres forståelse af repræsentationen. I arbejdet med de naturlige tal har opmærksomheden været på tallenes rækkefølge og indbyrdes placering – altså at vi fortløbende kan tælle frem og tilbage på linjen. I arbejdet med placering af brøker skal opmærksomheden i højere grad rettes mod, hvad vi betragter som det hele, der herefter skal deles. Fx kan vi finde $\frac{3}{4}$ ved at dele længden mellem 0 og 1 i fire og herefter tælle eller måle sig frem ved at se på $\frac{1}{4}, \frac{2}{4}$ pg $\frac{3}{4}$. Der bruges således en del-helhed-forståelse til at finde delen, altså stambrøken, som vi bruger til at måle med, så der bygges videre på denne forståelse fra fase 2.
Fase 3
At kunne identificere og bruge stambrøken som en måleenhed til at finde størrelsen af en længde.
Skilte til pytonslanger i zoo
En zoo vil lave nye skilte, som passer til deres pytonslanger. De vil derfor måle længden af de forskellige slanger, så de kan lave skilte, der fortæller og viser, hvor lange de forskellige slanger er.
Læreren har klippet kasseboner ud i forskellige længder og starter med at hænge slangen Gunnar op på væggen eller tavlen.
Starten af lektionen handler om, hvordan vi kan måle den lange slange Gunnar. Hvordan måler vi den?
Gunnar måles sammen på klassen, fx ved at en elev kommer op til tavlen og måler med en meterlineal (Gunnar skal være 1 meter lang). Herefter hænger læreren den lidt længere slange, Ursula, op på tavlen (Ursula er $1\frac{1}{3}$ meter). Klassen starter med at diskutere, hvor lang den cirka er, og om den er over eller under en meter. Hvordan beskriver vi en længde, som er mere end 1 meter? Hvor meget er den længde i forhold til en meter? Alle grupper får den sidste længde af Ursula, som vi ikke kender ($\frac{1}{3}$ meter), sammen med en meter. Det vil sige, at de får en strimmel, som er den længde, Ursula er længere end Gunnar. I gruppen diskuteres: Hvordan kan vi beskrive den længde? Hvor lang er den sammenlignet med en meter? Læreren samler op og taler om, hvordan vi ved, at længden er $\frac{1}{3}$ – få gerne elever op og vise på tavlen. Det vil sige, at eleverne fortsætter med at arbejde med symbolsproget fra fase 2. Det er vigtigt, at der meget nøjagtigt vises, hvordan vi lægger $\frac{1}{3}$ efter hinanden, så vi viser, at der er tre på den samlede meter.
Læreren begynder på et skilt, hvor der står: 'Gunnar 1 meter, Ursula $1\frac{1}{3}$ meter'. Herefter får grupperne to nye slanger: Mikkel og Asbjørn. Hvor lange er de? (Mikkel er $\frac{1}{4}$ meter, og Asbjørn er $\frac{1}{5}$ meter). Det kan fx gøres, ved at eleverne ser, hvor mange gange Mikkel kan ligge inde i Gunnar. Grupperne arbejder på at finde længden på de sidste slanger og skriver brøken. Læreren får hver gruppe til at præsentere deres bud på skilte med længden på slangerne, og hvordan de er nået frem til slangernes forskellige mål.
Herefter præsenterer læreren den helt nye slange, som zoo netop har købt. Den hedder Siv (den er $\frac{2}{5}$ meter). Herefter diskuterer eleverne i gruppen, hvor lang den nye slange er, og laver skiltet færdigt. Herefter taler de med en af de andre grupper: Er de enige om længden på slangerne? Opsamlingen skal fokusere på Siv. Hvordan kan vi finde ud af, hvor lang hun er? Igen måles der, hvor mange gange Siv kan være inde i Gunnar, men det går ikke præcist op... Hvordan kan vi lave en mindre enhed, som går op, og samtidig finde ud af, hvor lang Siv er? Et forslag kan være at folde Siv på midten og måle med denne længde – eller se på længden, der er for meget over 1 meter, når vi deler den op. Kan vi bruge den viden? Siv er vanskeligere at finde længden på, da hendes længde ikke er en stambrøk. I næste del af fasen laves en tallinje på en meter, der går fra $0$ til $2$, hvor længden på de forskellige slanger skrives ind som nedenfor:
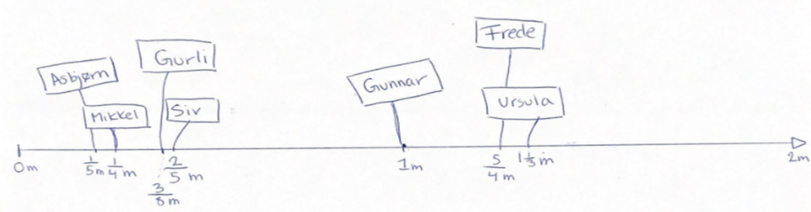
Arbejdet fortsætter med at formidle slangernes længde, ved at eleverne arbejder selvstændigt med nye slanger på en tallinje på et stykke papir. Tallinjen skal være $24$ centimeter lang og gå fra $0$ til $2$. Eleverne får oplysninger om nye slanger, som de skal lave og sætte ind på tallinjen. Fx er Gurli $\frac{3}{8}$ meter, og Frede er $\frac{5}{4}$ meter. Det centrale er her, at eleverne starter med at finde stambrøken og bruger den til at finde frem til forskellige længder. Fx ved en slange, som er $\frac{3}{8}$ meter, findes $\frac{1}{8}$ meter ved inddeling, og herefter 'tælles' frem til $\frac{3}{8}$ meter. Det vil sige $\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}$. Brøkerne, der arbejdes med, kan med fordel have tallene $2$ til $12$ i nævnere, hvor $7$ og $11$ i første omgang undlades. Fasen tager afsæt i den kendte repræsentation af slangen fra fase 2 og bygger videre med at få opbygget forståelsen af at kunne angive en længde gennem en brøk, som kan placeres på en tallinje.
Til slut sætter læreren to slanger op på tavlen over og under tallinjen og spørger, om vi kan finde en slange, der ligger imellem de to slanger. Hvor lang kunne den slange være?
Efter at grupperne har arbejdet med dette problem, tager læreren den mellemste slange og den længste slange og spørger igen: Kan vi finde længden på en ny slange, der er kortere end den længste, men længere end den korteste? Gennem dette arbejde arbejdes med en ny forståelse af tallenes ’tæthed’ – og dermed arbejdes med at overkomme denne distraktor.
Det centrale er bl.a. at give eleverne mulighed for at:
- erfare, hvordan stambrøken optræder i notationen.
- opdage, at tælleren angiver antallet af stambrøker.
- opbygge viden om, hvor mange stambrøker der går på en hel, fx $\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{4}{4}=1$.




Fase 4
I denne fase arbejdes med forholdet mellem tæller og nævner. Fasen kan fx strække sig over 4 lektioner.
Fase 4
At kunne anslå størrelsen på brøkerne gennem arbejdet med forholdet/ratioen mellem tæller og nævner.
Sortering af fisk i akvarium
Det følgende problem viderefører scenariet fra zoologisk have:
Dyrepasseren Sandra skal sortere fiskene i det store akvarium. Hun har fået at vide, at hun først skal sortere alle fiskene. De fisk, som er længere end en halv meter, skal i det ene akvarium, og de fisk, som er under en halv meter, skal i det andet. Fiskene er målt til:
$\frac{3}{8}m, \frac{16}{31}m, \frac{14}{25}m, \frac{5}{9}m, \frac{8}{5}m, \frac{1}{4}m,\frac{24}{49}m$
Eleverne taler med hinanden om, hvilke fisk der skal i hvilket akvarium, og læreren samler op på aktiviteten: Kan I finde en smart måde at se, om en brøk er over eller under en halv meter? Er der andre måder? Hvordan er måderne ens og forskellige? Scenariet kan føres videre:
Da Sandra er supergod til at sortere fiskene, bliver hun sat til at sortere fisk til tre nye akvarier. Fiskene, som er bittesmå, kommer i det første akvarie, så de ikke bliver spist. De skal altså være tæt på $0$ meter lange. De kæmpestore fisk, som er tæt på $1$ meter, kommer i det sidste akvarium. Mens de fisk, som er midt imellem – altså omkring en halv meter – kommer i det midterste akvarium. Fiskene er målt til:
$\frac{87}{88}m, \frac{13}{24}m, \frac{3}{17}m, \frac{10}{21}m, \frac{25}{49}m, \frac{1}{20}m,\frac{2}{5}m, \frac{2}{3}m, \frac{7}{9}m$
Læreren introducerer opgaven ved fx at tage afsæt i fisken, som er $\frac{2}{3}m$, og stiller spørgsmål som: Hvad tænker vi? Hvor skal Sandra putte fisken hen? Er den tættest på $0$, $1$ eller en halv meter?
Her kan det være en idé at stille spørgsmålet: Ved vi, hvilke brøker der er præcis midt imellem $\frac{1}{2}$ og $1$ meter? Netop i brøken $\frac{3}{4}$ er forskellen mellem tæller og nævner $1$, så hvis vi ræsonnerer ud fra blot forskellen, så kan vi konkludere, at brøken er tættest på $1$. Eller kan vi det? Eleverne skal altså argumentere imod denne generalisering. Alternativt kan vi tegne længderne $\frac{2}{3}, \frac{3}{4}$ og $\frac{7}{8}$ ind på en tallinje og herefter vurdere brøkernes værdi. Det centrale er, at vi ikke kan anslå værdien af brøken ved blot at trække tæller og nævner fra hinanden.
Eleverne arbejder herefter med at sortere fiskene. Læreren samler op på tavlen: Hvordan fandt I ud af, hvor fiskene skulle være? Hvilke strategier brugte I? Hvilke var lette og hvorfor? Hvilke var sværere og hvorfor?
Bagefter kan der arbejdes videre generelt med at placere forskellige brøker efter værdi.
Det centrale er bl.a. at give eleverne mulighed for at:
- erfare, at forholdet mellem tæller og nævner angiver værdien af brøken.
- erfare, at det ikke blot er forskellen mellem tæller og nævner, som er central, men at nævnerens (eller tællerens) værdi også har en betydning, når vi vurderer brøkens størrelse. Det vil sige, at $\frac{87}{88}$ og $\frac{2}{3}$ er ikke lige store, blot fordi der i begge er $1$ i forskel mellem tæller og nævner.

Fase 5
Fase 5 strækker sig over én til to uger (4-8 lektioner). Fasen handler om, at en klasse skal opbygge et brøkbegreb, så de kan operere på en mængde eller en størrelse – altså betydningen operator. Klassen kan fx arbejde med, hvor meget $\frac{3}{4}$ er, når det hele er $24$ (fx antal elever i klassen). Der opstår naturlige sammenhænge mellem del-helhed og det at finde ud af, hvad en stambrøk udgør for at finde det hele.
Første del af fasen tager afsæt i at kunne tage en stambrøk af en mængde – det vil sige at kunne tage $\frac{1}{2}$ eller $\frac{1}{3}$ af fx $12$ bolsjer (svarende til at multiplicere $12$ med $\frac{1}{2}$ eller $\frac{1}{3}$). Alle elever i klassen sidder med bunker af $12$ centicubes.
Fase 5
At kunne bruge brøken som en operator til at tage en del af en mængde – altså brøken opererer på en anden størrelse.
Farver på papegøjerne
Et forslag til en opstart kan være følgende:
Scenen er stadig sat i zoologisk have – men nu ved papegøjerne. Læreren tegner otte lige store fugle på tavlen, hvor $\frac{1}{4}$ af fuglene er blå, og resten er røde.
Klassen starter med en samtale om, hvor mange af fuglene der er blå. Hvordan kan vi vide det? Herefter fortsætter scenen ved, at vi går til et nyt papegøjebur, som vises på tavlen. I det nye bur er der 12 optegnede fugle, som endnu ikke er farvelagte. Læreren læser, at på skiltet til buret står der, at kendetegnet ved denne papegøjeart er, at $\frac{1}{3}$ af papegøjerne bliver født helt gule, mens resten bliver født helt røde. Herefter taler eleverne med deres makker om: Hvor mange papegøjer inde i buret skal være gule? Og røde?
Der samles op på tavlen, og det diskuteres, hvordan vi finder $\frac{1}{3}$, og hvordan vi kan være sikre på, at det netop er en $\frac{1}{3}$, vi har fundet. Et videre eksempel på en opgave kunne være:
På skiltet ved det næste papegøjebur står der, at $\frac{1}{2}$ af fuglene er helt røde, $\frac{1}{3}$ er helt blå, og $\frac{1}{6}$ er helt hvide. Hvor mange papegøjer kan det være, der er i buret?
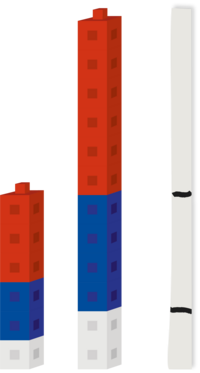
Eleverne arbejder herefter i grupper. De får centicubes i de tre farver og forsøger at komme med forskellige løsninger, som kan passe. Når der samles op på elevernes arbejde, kan det være en god idé at sætte centicubes sammen til forskellige stænger, hvor farverne er samlet, så den enkelte stang har den samme rækkefølge af farver; fx rød, blå og hvid. Stængerne vil således tydeligt vise, at der skaleres op og ned. Forholdet mellem farverne er dermed den samme på tværs af stængerne. Vi kan eventuelt tage en bred elastik og klippe den af i den længde, der passer til det mindste tårn. På elastikken markeres med tuschstreg $\frac{1}{2}, \frac{1}{3}$ og $\frac{1}{6}$ af elastikken. Eleverne kan eventuelt også lave hver deres egen elastik. Når vi strækker i elastikken så den passer med længden på et af de andre tårne, vil vi se tuschstregerne også passer til dem. Elastikken er en konkret operator, som kan tage tuschstreg $\frac{1}{2}, \frac{1}{3}$ og $\frac{1}{6}$ af alle længder.
I næste del af denne fase arbejdes med ægte brøker, som ikke er stambrøker.
Et eksempel på en opgave kan være:
En dag har dyrepasseren, Sandra, glemt at lukke døren ind til buret, og $\frac{2}{5}$ af papegøjerne er fløjet ud af buret. Der er 20 fugle tilbage i buret, så der er en del fugle, som er fløjet ud.
Eleverne kommer i grupper og skal forsøge at finde ud af, hvor mange fugle der er fløjet bort. Hver gruppe får 20 fugle som centicubes. Herefter samles op på klassen. Hvordan kan vi finde ud af, hvor mange fugle der er væk? Den videre opgave kan være:
Næste dag tænker dyrepasseren: ”Jeg må hellere lade døren stå åben ind til buret, så de fugle, som er fløjet bort, kan komme hjem og flyve ind i buret”. Desværre får flere af fuglene lyst til at flyve ud, så $\frac{3}{4}$ flyver nu ud tidligt om morgenen.
Eleverne arbejder i grupper med at finde ud af, hvor mange fugle der er tilbage, når dyrepasseren kommer for at fodre dem. Eleverne arbejder selv med opgaver, hvor der skal tages forskellige brøkdele af mængder. Denne del af arbejdet er også knyttet til en erfaring om, at den størrelse eller mængde, som en brøk repræsenterer, afhænger af den størrelse eller mængde, som brøkdelen tages af. Samtidig lægges der grunden til den videre forståelse af, at multiplikation ikke altid giver et større resultat. I slutningen af fasen kan der evt. arbejdes med at regne den anden vej.
En sådan opgave kan være:
Direktøren for den zoologiske have bliver meget sur på dyrepasseren, da han ser, der kun er fire fugle tilbage i buret. Han spørger: ”Hvor mange fugle har vi mistet?”. Dyrepasseren tænker sig længe om og siger så: ”Vi har stadig $\frac{1}{4}$ af papegøjerne, så det er jo ikke så galt”. Har dyrepasseren ret?
Det centrale i denne fase er bl.a. at give eleverne mulighed for at opdage:
- at en brøkdel af noget ikke er konstant, men det afhænger af den helhed, som eleverne tager brøken fra.
- at stambrøken er central, når eleverne skal finde andre brøkdele.