At dividere flercifrede tal
Introduktion
Dette læringsspor retter sig mod elevers udvikling af strategier til at dividere flercifrede, naturlige tal. Det er tænkt til mellemtrinnet, fx med start i 4. klasse. Set i forhold til stofområdet ’tal og algebra’ i grundskolen vedrører det tal og regnestrategier, som vist på figur 1 herunder.
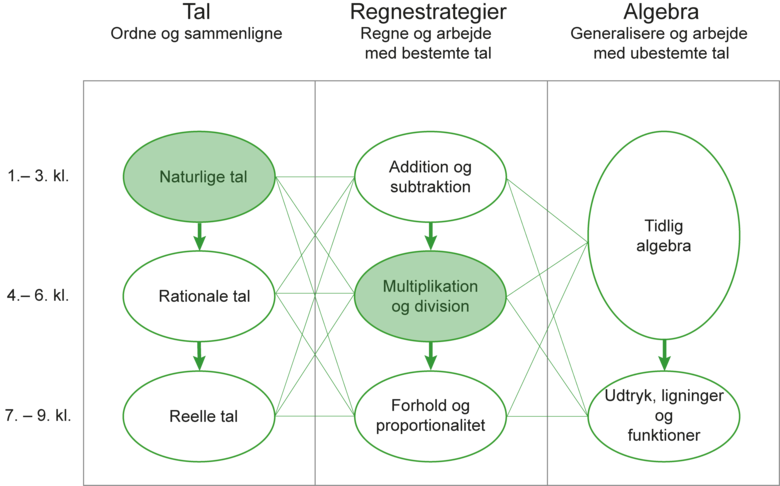
Læringsspor til grundskolen udviklet af NCUM under den fælles indsats for tal og algebra.
Udgivet 2025
Forfattere på læringsssporet er Thomas Kaas, Charlotte Krog Skott, Morten Blomhøj og Marit Hvalsøe Schou.
En strategi til at dividere flercifrede naturlige tal vedrører den måde, man håndterer dividend og divisor med henblik på at finde frem til resultatet (Hickendorff et al., 2019).
Mål
Læringssporets har to overordnede mål, som hænger sammen:
-
Det skal bidrage til, at eleverne udvider deres forståelser for egenskaber ved flercifrede, naturlige tal og regningsarten division.
-
Det skal gøre eleverne i stand til at dividere flercifrede tal fleksibelt.
Elever, der er kommet langt i forhold til mål 1, forstår bl.a., at de kan opdele flercifrede tal på forskellige måder og udnytte opdelingerne til division. De ved fx, at de kan opdele tallet $784$ i $700 + 84$ eller i $700 + 70 + 14$ og tænke divisionen $784 : 7$ som $700 : 7 + 84 : 7$ eller som $700 : 7 + 70 : 7 + 14 : 7$.
Elever, der er kommet langt i forhold til mål 2, kan bl.a. dividere firecifrede tal med etcifrede og enkelte tocifrede tal – ved at bruge papir og skriveredskaber som hjælpemidler. De råder over et repertoire af forskellige strategier til sådanne beregninger, de kan vælge en strategi, der er hensigtsmæssig i et givent problem, og de kan foretage beregninger rimeligt effektivt. Hvis de skal beregne $1248 : 8$, kan det fx være, at de bruger opdelinger og tænker: $1248 : 8 = 800 : 8 + 400 : 8 + 48 : 8 = 100 + 50 + 6 = 156$.
Hvis de skal beregne $792 : 8$, kan det derimod være, at de først beregner $800 : 8$ og derefter ’kompenserer’ ved at beregne $100 - 8 : 8 = 99$.
De to mål hænger sammen på den måde, at elevernes forståelser er en forudsætning for, at de kan multiplicere flercifrede tal fleksibelt. Omvendt udvikles deres forståelser igennem arbejdet med at multiplicere fleksibelt.
At dividere fleksibelt vil sige at have et bredt repertoire af strategier til division og at kunne vælge og tilpasse en (eller flere) af disse strategier til en bestemt situation eller beregning (Hickendorff et al., 2019).
At dividere effektivt vil sige at kunne dividere uden fejl, og at beregningerne ikke er (for) tidskrævende (National Research Council, 2001).