Praksis – At dividere flercifrede tal
De tidsmæssige rammer
I de fleste klasser vil det være passende at begynde læringssporet i 4. klasse.
I de fleste klasser vil det være hensigtsmæssigt at lade læringssporet strække sig over flere undervisningsforløb. Det kan fx dreje sig om to forløb á 3 uger på tværs af to skoleår, fx 4. klasse og 6. klasse.
Opdelingen mellem de to forløb kan være efter fase 2 eller efter fase 3. Hvis opdelingen er efter fase 3, vil det være en god idé at gentage dele af 3. fase, sådan at det nye forløb begynder med yderligere fokus på udvikling af fleksible og effektive strategier.
I hvert forløb kan det være en god idé at supplere det faglige indhold med øvelser, fx i form af lege og spil, der giver eleverne mulighed for fortsat at få rutine i division med mindre tal.
Det faglige udgangspunkt
Division af flercifrede tal bygger videre på tidligere undervisning, især på elevers tidligere arbejde med multiplikation. Oversigten viser lidt mere specifikt fire forudsætninger, som læringssporet bygger på.
For det første er det en forudsætning, at eleverne har kendskab til situationer, der vedrører division med mindre tal, herunder både ligedelingsdivision og målingsdivision. I forbindelse med ligedeling kan det fx dreje sig om $4$ børn, der skal dele $12$ karameller lige. Hvor mange karameller får de hver? I forbindelse med måling kan det fx dreje sig om, at karamellerne skal puttes i poser. Der skal være $4$ karameller i hver pose. Hvor mange poser bliver der? I temaet om etcifrede beregninger på matematikdidaktik.dk er disse situationer omtalt yderligere.
For det andet er det en forudsætning, at eleverne tidligere har arbejdet (lidt) med strategier til multiplikation af flercifrede tal. Denne forudsætning giver eleverne gode muligheder for at løse divisionsproblemer med sekventielle strategier. Om divisionsproblemet til højre kan de fx tænke: 'Hvor mange gange kan $4$ ’være inde i’ $48$? Jeg ved, at $10$ gange $4$ er $40$… Hvis jeg tager $4$ én gang mere kommer jeg op på $44$… og én gang mere, så bliver det $48$. Altså $12$ poser i alt'.
For det tredje er det en forudsætning, at eleverne har prøvet at opdele tal. Denne forudsætning giver eleverne gode muligheder for at løse divisionsproblemer med opdelingsstrategier. Om divisionsproblemet med de 48 æbler kan de fx tænke: 'Jeg kan dele $48$ op i en bunke med $40$ og en bunke med $8$. Jeg kan først finde det antal poser, jeg skal bruge til den ene bunker, og bagefter det antal, jeg skal bruge til den anden bunke'.
For det fjerde er det en forudsætning, at eleverne er nogenlunde fortrolige med addition og subtraktion. Eleverne kan få brug for at addere eller subtrahere i forbindelse med alle strategierne. Hvis eleverne fx begynder at løse problemet med de 48 æbler ved at tænke, 'jeg begynder med $5$ poser, så jeg på den måde får klaret $20$ af æblerne', så har de brug for at beregne $48 - 20$ for at beregne, hvor mange æbler der er tilbage.
Du skal putte 48 æbler i poser.
Der skal være 4 æbler i hver pose.
Hvor mange poser får du brug for?
Fase 1
Den første fase kan fx vare en uge (4 lektioner) og handler primært om, at eleverne – ud fra deres forskellige forudsætninger – løser divisionsproblemer, som de får præsenteret mundtligt af læreren. Problemerne bør være knyttet til en kontekst, som eleverne kan forestille sig, og som giver dem rige muligheder for at bruge konkrete materialer eller egne tegninger som støtte. Desuden skal problemerne være så tilpas udfordrende for eleverne, at de giver en grund til at lede efter ’smarte’ måder eller genveje til løsninger. Den type udfordring får eleverne typisk, hvis problemet kræver division af et to- eller trecifret tal med et etcifret tal, uden at læreren på forhånd har fortalt, hvordan opgaven kan løses.
Et karakteristisk eksempel på et sådan problem er opgaven fra 'Lige store grupper' med målingsdivison:
Fase 1
At løse hverdagsproblemer, der involverer flercifret division med støtte i konkrete materialer og tegninger.
Forældremøde på skolen
Vi skal holde forældremøde på skolen. Der kommer $84$ forældre. Ved hvert bord kan der sidde $6$ forældre. Hvor mange borde får vi brug for? (Bearbejdet efter Treffers, 1991).
Læreren kan fx sætte scenen ved at fortælle om et forældremøde, der skal afholdes på en skole, om de forældre, som havde meldt, at de vil deltage – og om, hvordan der nu skulle gøres klar til forældremødet med bl.a. bordopstilling. Han kan evt. tegne et bord med seks stole for at antyde, hvordan eleverne selv kan lave skitser, når de efterfølgende skal arbejde med problemstillingen.
Eleverne arbejder herefter alle i smågrupper med problemet, fx 15-20 minutter. Det er godt, hvis alle grupper – eller stort set alle – når til et bud på resultatet. De grupper, der bliver hurtigt færdige, kan evt. arbejde med udvidelser af opgaven. Hvad nu, hvis der havde været $114$ forældre? Undervejs observerer læreren, hvilke strategier eleverne bruger, og han støtter og udfordrer dem, fx ved at komme med forslag, der ligger i forlængelse af elevernes egne tanker.
En elevgruppe begynder arbejdet med at tegne firkanter for borde, lægge $6$ centicubes på hvert ’bord’ og tælle. ’Et bord, $6$ forældre, to borde, $12$ forældre, tre borde…’. Læreren anerkender eleverne fremgangsmåde, men siger også, at der godt nok er langt op til $81$. Han spørger, om det kan være en idé for dem at tælle flere borde ad gangen, fx $2$ borde ad gangen.
Som beskrevet under Tilgang kan det tænkes, at eleverne bruger mange forskellige strategier til at nå frem til resultatet. En efterfølgende fælles samtale i klassen fokuserer netop på at dele disse fælles strategier, så eleverne får mulighed for at reflektere over flere forskellige måder at tænke division på. I disse samtaler er det primært lærerens opgave, at de forskellige strategier bliver tydelige for klassen. Han kan støtte refleksionerne ved at reformulere og præcisere nogle af elevernes forklaringer og evt. ved at illustrere idéerne med konkrete materialer, tegninger og talsymboler.
En elevgruppe forklarer, hvordan de har lavet bunker med $6$ centicubes i hver. De har brugt $6$-tabellen og holdt regnskab med antallet af bunker.
Læreren tegner deres forklaring som til højre på tavlen.
Det kan være en fordel, hvis læreren på baggrund af sine observationer af elevernes arbejde har valgt en rækkefølge, grupperne skal fortælle i. Nogle grupper har brugt mere sofistikerede og effektive strategier end andre.
En af grupperne har udnyttet, at $10$ borde svarer til $60$ personer, fordi $10 \cdot 6=60$. Læreren lader denne gruppe præsentere deres arbejde senere end gruppen, der har bygget på deres kunnen om $6$-tabellen. Han illustrerer deres beskrivelse som tegningen til højre.
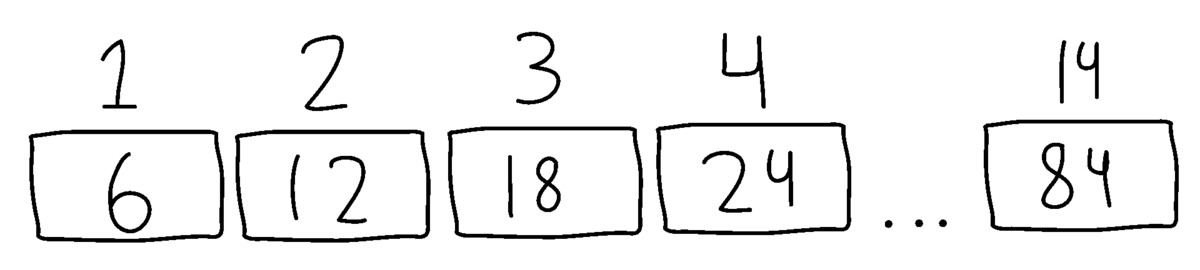

I fase 1 fortsætter klassen arbejdet med flere fortalte divisionsproblemer. De arbejder i en vekslen mellem iscenesættelse af problemet, selvstændigt arbejde i små grupper og fælles samtaler i klassen. Den følgende problemstilling vedrører en målingssituation på samme måde som den første, men derefter veksler læreren problemerne, så de også kommer til at vedrøre ligedelingsdivision. Problemerne kan fx være:
Læreren vil lave kaffe til de $84$ forældre. Alle skal have mulighed for at få én kop kaffe. Hver kande giver $7$ kopper. Hvor mange kander skal hun lave?
Ved hvert bord får de $6$ forældre en pakke med pebernødder. Der er $96$ pebernødder i hver pakke. Hvor mange er der til hver forældre, hvis de deler dem lige?
Senere ved forældremødet skal forældrene deles i nye grupper, der skal snakke om årets hyttetur. Der skal være $4$ forældre i hver gruppe. Hvor mange grupper bliver der?
Fase 2
I 2. fase introducerer læreren tallinjen og ’skålene’ som repræsentationer for divisionssituationer. Hensigten er, at disse repræsentationer skal kunne støtte elevernes udvikling af strategier og forståelse af egenskaber ved de naturlige tal og division. Samtidig kan tallinjen og skålene støtte overgangen til matematisk symbolsprog.
I introduktionen er det vigtigt, at både tallinjen og skålene bliver tæt forbundet med elevernes egen tænkning – de to repræsentationer skal netop hjælpe eleverne med at bringe deres tænkning på symbolsk form. I sammenhæng med problemet med bordene til forældremødet kan introduktionen fx foregå, når en gruppe forklarer, hvordan de har løst problemet. Eksemplet herunder antyder, hvordan en sådan introduktion kan begynde.
Fase 2
At dividere flercifrede tal med støtte i tegninger og talsymboler.
Borde og tallinjen
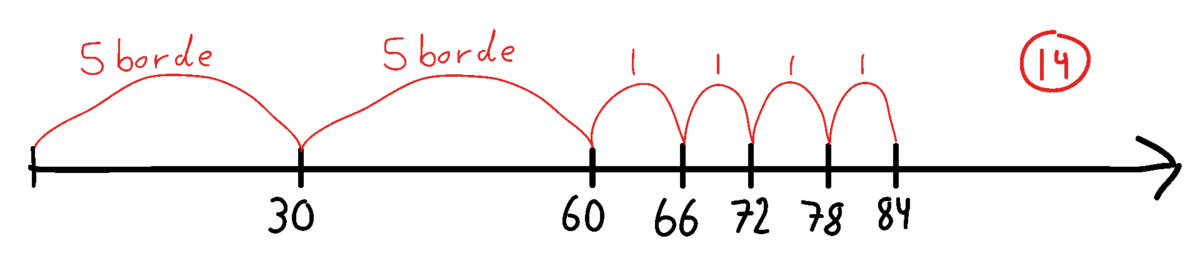
Lise: Vi tog først $5$ borde. Det passer til $30$ forældre. Så tog vi $5$ borde mere. Det er $60$ forældre. Til sidst tog vi bare $1$ bord ad gangen, til vi kom op på $84$ forældre. Det blev $14$ borde i alt.
Lærer: Aha. Jeg vil lige være helt sikker på, at jeg forstår, hvad I mener. Jeg vil prøve at vise det, I siger, på en tallinje (se tegningen til højre). Så må I alle sammen holde øje med, om I er enige i, at jeg har forstået det rigtigt…
Lærer: Kan I se, hvad min tegning viser? Er I enige i, at den viser det, Lise sagde?
På tilsvarende måder kan skålene introduceres. Det kan fx være i sammenhæng med situationen, hvor $6$ forældre skal dele $96$ pebernødder.
Skåle og pebernødder
Noah: Vi tænkte, at der i hvert fald kan blive $10$ til hver, så vi begyndte med at dele $10$ ud. Det blev $60$… og så er der kun $36$ tilbage.
Læreren griber forklaringen og illustrerer den som til højre.
Efterfølgende fortsætter klassen med at ligedele de resterende $36$ (pebernødder) mellem de $6$ (forældre).

Det er også en del af fase 2, at klassen arbejder med sammenhængen mellem forskellige divisionssituationer og det tilhørende regneudtryk, altså fx at udtrykket $84 : 6$ kan beskrive den situation, hvor nogle lærere skal finde ud af, hvor mange borde der skal bruges til $84$ forældre (når der kan sidde $6$ forældre ved hvert bord). I den forbindelse kan det være hensigtsmæssigt at få eleverne til (også) at bevæge sig den modsatte vej. 'Hvilket problem kan høre til udtrykket $114 : 6$?'. En sådan opgave kan give læreren indsigt i, om eleverne kan koble mellem det matematiske udtryk og en omverdenssituation, og om eleverne både kan forbinde udtrykket med målingssituationer og ligedelingssituationer.
Når eleverne kan forbinde divisionsudtryk som $115 : 5$, $224 : 6$, $224 : 7$ osv. med situationer, som de kan ’tænke igennem’’, kan der i undervisningen også – indimellem – indgå opgaver, der er givet i rent symbolsprog (og ikke nødvendigvis med en tilhørende iscenesættelse). Det er dog vigtigt, at læreren løbende kontrollerer, om eleverne kan forbinde forskellige situationer med dem.
Fase 3
Denne fase handler primært om, at eleverne fortsat skal udvikle deres strategier til division, så de bliver bedre til at dividere fleksibelt og effektivt. Eleverne får mulighed for en sådan udvikling, når de ser, afprøver og reflekterer over hinandens strategier med lærerens støtte. Lærerens opgave er bl.a. at fremhæve centrale pointer om division. Disse pointer knytter sig primært til de tre typer af strategier, der er beskrevet under Tilgang. Det er altså pointer, at man kan dividere direkte eller indirekte, og at man kan bruge sekventielle strategier, opdelingsstrategier og kompensationsstrategier; men det er ikke hensigten, at eleverne skal kende disse begreber.
Eksemplerne herunder viser, hvordan læreren kan fremhæve pointer vedrørende strategier til division.
Fase 3
At dividere flercifrede tal fleksibelt med støtte i tegninger og talsymboler.
Eksempel om direkte og indirekte divison
Eleverne har arbejdet med forældremødeproblemet, der er forbundet med divisionen $84 : 6$. Mange elever har brugt indirekte division, men der er også nogle elever, der har brugt direkte division. Læreren fremhæver dette:
Lagde I mærke til, at gruppen med Lise begyndte med $6$ borde og talte op til $84$ forældre… men gruppen med Ole begyndte med de $84$ forældre og talte nedad (viser tegninger på tavlen). De nåede frem til det samme resultat. Det kunne se ud som om, at man kan begynde i hver sin ende? Er det rigtigt? Hvorfor?
Eksempel om opdeling
Eleverne har arbejdet med deling af pebernødder, der er forbundet med divisionen $96 : 6$. Mange grupper har i deres løsninger brugt forskellige opdelinger af $96$. Læreren fremhæver dette:
Jeg lagde mærke til, at mange af jer først tog nogle af pebernødderne. Gruppen med Liva sagde fx: 'Vi deler først $60$ ud. Så er der $36$ tilbage' (viser tegning på tavlen). Det ser ud som om, at I har delt $96$ op i $60$ og $36$, som I har delt ud. Hvorfor valgte I lige $60$? Kunne I også have valgt at dele op på en anden måde? Kunne I også have delt op, hvis det var $200$ pebernødder? Eller $300$? Kan man altid dele tal op? Hvorfor?
Eksempel om kompensationsstrategi
Eleverne har arbejdet med divisionen $96 : 6$. En gruppe har tegnet skåle for at løse problemet. I deres præsentation fortæller de, at de faktisk kunne nøjes med at tænke $48 : 3$.
Hvis vi deler halvdelen af pebernødderne op i halvdelen af skålene, så ved vi jo, at der kommer lige så mange i de sidste skåle, siger de.
Klassen er enige i dette argument, og læreren spørger: 'Okay, kan I bruge samme fidus, hvis det er $20$ pebernødder til $4$ personer? Hvad med $30$ pebernødder til $6$ personer? Kan man altid bare tage halvdelen af tallene, når man dividerer?'
I nogle klasse opstår de forskellige strategier blandt eleverne. I andre klasser må læreren tage initiativ til, at eleverne kommer til at se, bruge og forstå strategier til division.
Et andet fokuspunkt i fasen er, at eleverne i større og større grad begynder at vælge strategier, der er tilpassede netop de problemer, de skal løse, og de tal, der indgår i dem. For en elev, der ved, at $100 \cdot 5 = 500$, kan det i divisionen $515 : 5$ fx være hensigtsmæssigt at vælge en opdelingsstrategi og dele $515$ op i $500$, $10$ og $5$. Det betyder dog ikke, at det altid er hensigtsmæssigt at opdele trecifrede tal i $100$´ere, $10$´ere og $1$´ere. I divisionen $168 : 6$ kan det fx være hensigtsmæssigt for den samme elev at opdele $168$ i $60$, $60$ og $48$. Eleverne får mulighed for at udvikle denne side af deres fleksible tænkning, når klassen sammen – med lærerens støtte – afprøver og diskuterer forskellige strategier til det samme divisionsproblem.
Fase 4
Fokus i denne sidste fase er på brug af matematisk symbolsprog i forbindelse med beregninger og omskrivninger. Hidtil har eleverne støttet til sig til konkrete materialer, egne tegninger, tallinjen, skålene og evt. talsymboler. Et af målene i læringssporet er, at eleverne gradvist slipper de konkrete og billedlige repræsentationer og vænner sig til at ’tænke i’ matematisk symbolsprog med talsymboler, regnetegn og lighedstegn.
Som en overgang til almindelige regneudtryk kan det for nogle elever være en fordel, hvis læreren viser en af de skrivemåder, der er præsenteret under Fase 4 i Tilgang. Det er en god idé, hvis introduktionen foregår, så den er tæt knyttet til elevernes tænkning. Den kan fx foregå i forlængelse af en forklaring fra en elev, der har gennemført en division med en opdelingsstrategi:
Fase 4
At dividere flercifrede tal fleksibelt med støtte i regneudtryk.
Fra skåle til symbolsprog
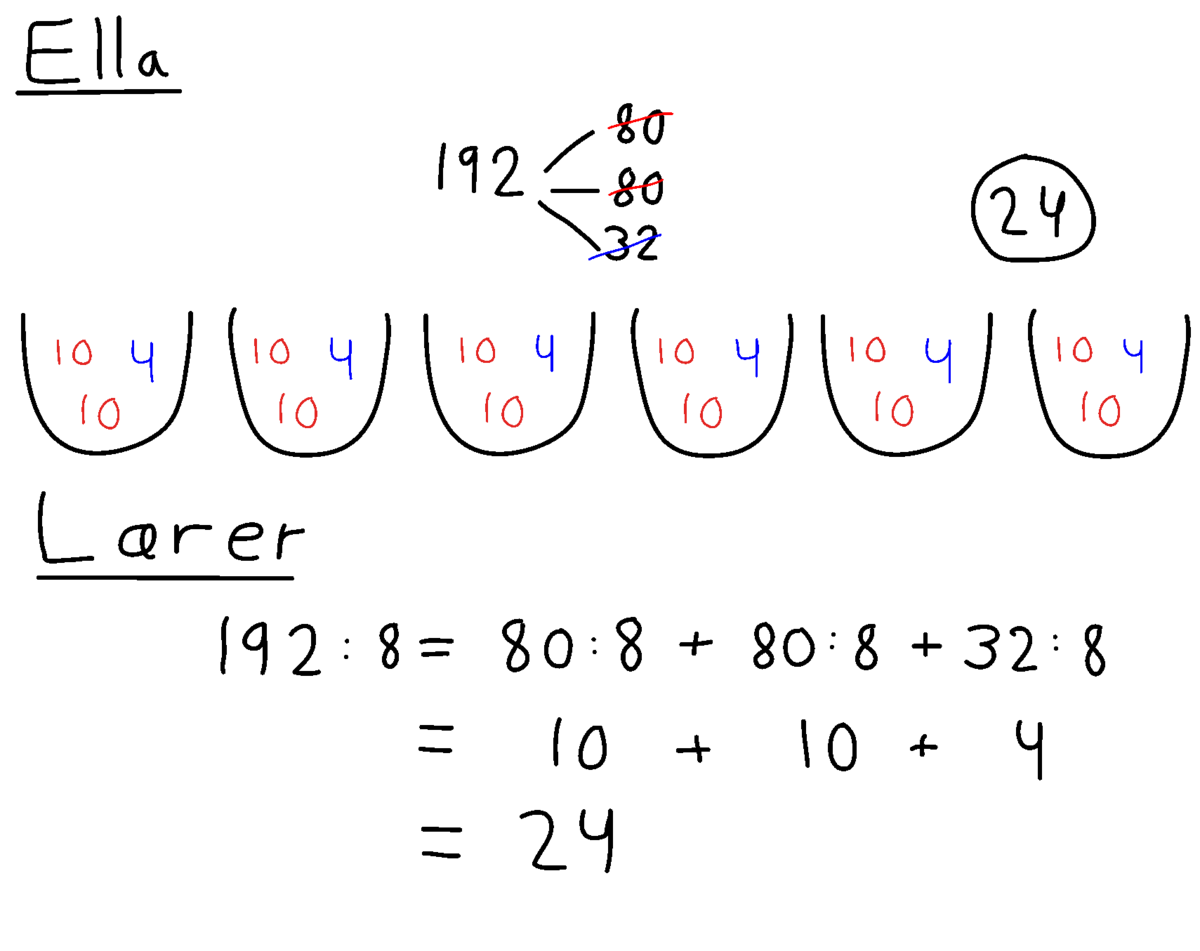
Ella: Vi løste $192 : 8$ med skålene. Vi delte $192$ op i $80 + 80 + 32$. Så kunne vi først give $10$ til hver. Det gjorde vi to gange. Så var der $32$ tilbage. Så kunne de få $4$ hver. Det bliver $24$ i alt.
(Eleven tegner som til højre, mens hun fortæller)
Lærer: Fint. Din tegning viser flot, hvordan I har tænkt. Måske behøver I ikke længere at tegne skålene, når I dividerer på den måde, du har fortalt? I kan også skrive det sådan (se tegning til højre).
Kan I se, hvordan jeg har skrevet, at I delte op i $80$, $80$ og $32$? Hver bunke delte I lige mellem $8$… eller man kan sige, at hvert tal dividerede I med $8$.
Det næste eksempel viser en introduktion til den anden skrivemåde, der er vist under Fase 4 i Tilgang. Denne introduktion ligger i forlængelse af en forklaring fra en elev, der har gennemført en division med en målingsstrategi:
Fra tallinje til symbolsprog
William: Vi tænkte på tallinjen, da vi løste $192 : 8$. Vi tog lidt ad gangen. Først $10$ gange $8$. Det er $80$. Så $10$ gange $8$ igen. Så kommer vi op på $160$. Så var der $32$ tilbage. Det passer med $4$ gange $8$.
(Eleven tegner som til højre, mens han fortæller)
Lærer: Fint. Din tegning viser flot, hvordan I har tænkt. Jeg vil vise jer en anden skrivemåde, som I kan bruge til at vise den samme måde at tænke på.
(Læreren tegner som til højre).
Kan I se, hvordan jeg har skrevet, at I først tog $10$ gange $8$, og at det blev $80$? Hvorfor tror I, at jeg har skrevet $112$? Hvad sker der i resten af det, jeg har skrevet?

Brug af matematisk symbolsprog bør ikke være begrænset til de viste metoder og skrivemåder. Med en kompensationsstrategi til beregningen af $192 : 8$ kan beregningen fx komme til at se sådan ud: $192 : 8 = 200 : 8 - 8 : 8 = 25 - 1 = 24$.
I praksis kan det ikke forventes, at alle elever i en klasse på samme tid er klar til at foretage de skift i brugen af repræsentationer, som læringssporet lægger op til. Nye måder at repræsentere på kan introduceres, efterhånden som ’passende situationer’ opstår (og i den rækkefølge, læringssporet omtaler), men det betyder ikke, at ’gamle måder’ skal droppes. Det er en mulighed, at eleverne sideløbende bruger forskellige måder at repræsentere på, og at nye måder løbende sammenlignes med måder, der tidligere er opstået i undervisningen.