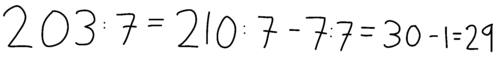Tilgang – At dividere flercifrede tal
Grundlæggende er der to bevægelser i læringssporet. Den ene går ud på, at eleverne gradvist udvikler fleksible måder at dividere på. Den anden går ud på, at eleverne gradvist udvikler deres måder at repræsentere den tænkning, de knytter til måderne. De to bevægelser foregår samtidigt over tid.
Udgangspunktet for de to bevægelser er elevernes arbejde med hverdagsproblemer, der involverer flercifret division. Man kan kategorisere sådanne hverdagsproblemer i fire typer multiplikative situationer:
- Lige store grupper
- Sammenligninger
- Rektangulære mønstre
- Kombinationer
ㅤ
Her er eksempler på hverdagsproblemer til hver af de fire situationer. I de situationer, hvor det giver mening, er eksemplerne er opdelt i ligedelingsdivision og målingsdivision:
Lige store grupper
Ligedelingsdivision: $6$ børn vil dele en klase med vindruer, så de får lige mange hver. Der er $84$ vindruer i klasen. Hvor mange vindruer kan børnene få hver?
Målingsdivision: Der kommer $84$ forældre til et forældremøde. Der kan sidde $6$ forældre ved hvert bord. Hvor mange borde bliver der brug for?
Rektangulære mønstre
Ligedelingsdivision eller målingsdivision: En terrasse med form som et rektangel består af $108$ (rektangulære) fliser. Terrassen har $9$ rækker. Hvor mange fliser er der i hver række?
Sammenligninger
Ligedelingsdivision: Victor har $84$ glaskugler. Han har $6$ gange så mange glaskugler som Alma. Hvor mange glaskugler har Alma så?
Målingsdivision: Victor har $84$ glaskugler, og Alma har $6$ glaskugler. Hvor mange gange så mange glaskugler har Victor i forhold til Alma?
Kombinationer
Ligedelingsdivision eller målingsdivision: Victor kan lave $48$ forskellige sæt tøj af sine forskellige bukser og bluser. Han har $8$ forskellige bluser. Hvor mange forskellige bukser har han?
En multiplikativ situation er et problem fra elevernes hverdag, som kan løses med multiplikation og/eller division (Verschaffel, Greer & De Corte, 2007).
Ligedelingsdivision vedrører multiplikative situationer, hvor multiplikanden er ukendt. Man kan løse problemer med ligedelingsdivision ved at ’dele ud, så alle får lige meget’. Det kan fx være et beløb, der skal deles lige mellem et antal personer.
Målingsdivision vedrører multiplikative situationer, hvor multiplikatoren er ukendt. Man kan løse problemer med målingsdivision ved at ’måle, hvor mange gange en størrelse kan være i en anden størrelse’. Det kan fx handle om, hvor mange bøger med en bestemt bredde, der kan stå på en hylde med en bestemt længde.
Fase 1
I fase 1 af læringssporet arbejder eleverne med et udvalg af de fire multiplikative situationer. Det er især vigtigt for det følgende arbejde, at de løser hverdagsproblemer af typen ’lige store grupper’ – både som ligedelingsdivision og måledivision. Eleverne løser hverdagsproblemerne med strategier, som de selv finder på, og med støtte i konkrete repræsentationer, tegninger og evt. talsymboler.
Man kan fx forestille sig, at nogle elever løser problemet med målingsdivision under eksemplet med ’Lige store grupper’ ved at:
- lave bunker med $6$ centicubes i hver og bruge $6$-tabellen til at holde regnskab med, hvornår de kommer til $84$.
- tegne borde, hvorpå de skriver ’$6$’. De bliver ved med at tegne, og addere, indtil summen når op på $84$.
- udnytte, at $10 \cdot 6$ er $60$, og at $10$ borde derfor giver plads til $60$ forældre. Derefter siger de ’$11$ borde giver plads til $66$ forældre, $12$ borde til $72$ forældre, osv.’ Måske skriver de noter for at huske antallene.
Tilsvarende kan man forestille sig nogle elever løse problemet med ligedelingsdivision under eksemplet med 'Lige store grupper' ved at:
- finde $84$ centicubes, som de fordeler i $6$ bunker. Måske deler de ud én ad gangen, måske uddeler de to eller tre ad gangen til hver af de $6$ bunker.
- tegne $6$ cirkler, der repræsenterer de seks børn, og sætter streger i cirklerne, indtil der $84$ streger i alt.
- udnytte, at $6 \cdot 10$ er $60$, og at $60$ vindruer derfor giver $10$ til hver. Derefter siger de, at der er $24$ vindruer tilbage, fordi $84 - 60$ er $24$. ’Så kan de få $4$ mere, for $4 \cdot 6$ er $24$’… Måske skriver de noter for at huske antallene.
Fase 1
At løse hverdagsproblemer, der involverer flercifret division med støtte i konkrete materialer og tegninger.
Der kommer 84 forældre til et forældremøde. Der kan sidde 6 forældre ved hvert bord. Hvor mange borde bliver der brug for?
6 børn vil dele en klase med vindruer, så de får lige mange hver. Der er 84 vindruer i klasen. Hvor mange vindruer kan børnene få hver?
Fase 2
I fase 2 introducerer læreren på baggrund af hverdagsproblemerne i fase 1 to repræsentationer, som eleverne kan bruge til at støtte deres tænkning. Den ene repræsentation er en åben tallinje (se læringssporet ’At subtrahere flercifrede tal’). Den anden repræsentation kalder vi ’skåle’.
Den åbne tallinje
Tallinjen er især egnet til at støtte tænkning, der er knyttet til problemer med målingsdivision. Eksemplerne herunder viser, hvordan den åbne tallinje kan bruges til at støtte tænkning knyttet til problemstillingen om bordene til forældremødet:
Her gives to eksempler på, hvordan den åbne tallinje kan bruges til at løse divsionsproblemet $84 : 6$.

De øverste buer viser $14$ ’hop’ á $6$. De nederste tal viser den samlede sum af $6$´ere. Resultatet er $14$.

De øverste buer viser et ’hop’ på $10 \cdot 6$ og et hop på $4 \cdot 6$. De nederste tal viser den samlede sum af $6$´ere. Resultatet er $14$.
Skåle
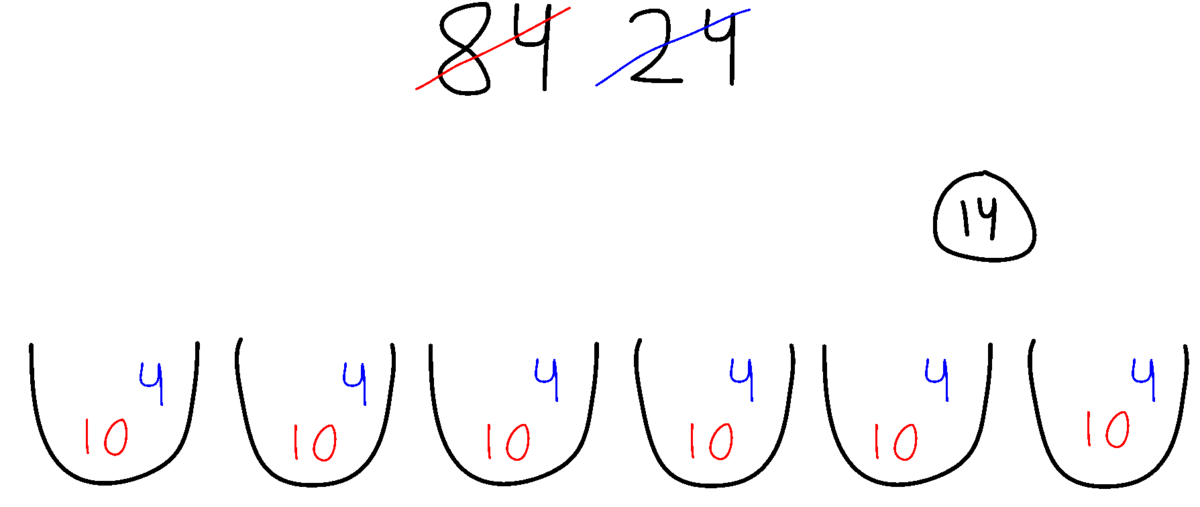
Repræsentation med skålene er især egnet til at støtte tænkning, der er knyttet til problemer med ligedelingsdivision. Eksemplet herunder viser, hvordan elever kan støtte sig til denne repræsentation for at løse ligedelingsproblemet under eksemplet med ’Lige store grupper’. Skålene repræsenterer det antal, der skal dele vindruerne (divisoren), og tallene repræsenterer det antal, der skal deles (dividenden).
Nedenunder ses et eksempel på at bruge skåle som repræsentation for at løse $84 : 6$. Først er der delt $10$ (vindruer) ud til hver (person). Der er $24$ tilbage. Nu kan hver (person) få $4$. Resultatet er $14$.
Fase 2
At dividere flercifrede tal med støtte i tegninger og talsymboler.
I fase 2 er det hensigten, at eleverne dividerer flercifrede tal med støtte i disse repræsentationer. Samtidig skal de påbegynde deres udvikling af strategier til division.
I løbet af fasen fokuserer undervisningen i mindre grad på hverdagsproblemer og i højere grad på multiplikation i en ren matematisk kontekst. Repræsentationerne gør det muligt, at eleverne i princippet kan tælle sig frem til resultatet af en division, men samtidig åbner det for, at de kan ’skyde genveje’ ved at anvende andre strategier end tælling.
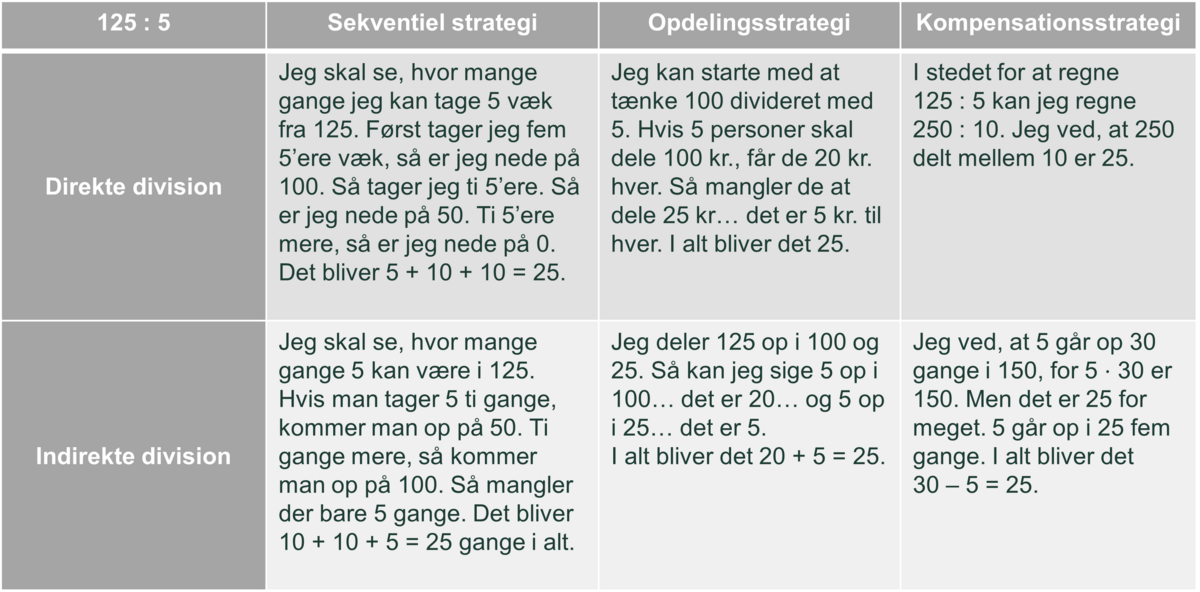
De strategier til division, som en klasse i fællesskab kan udvikle i læringssporet, kan generelt opdeles i tre typer (Hickendorff et al., 2019).
Fælles for de tre typer er, at division enten kan tænkes som direkte division eller som indirekte divison.
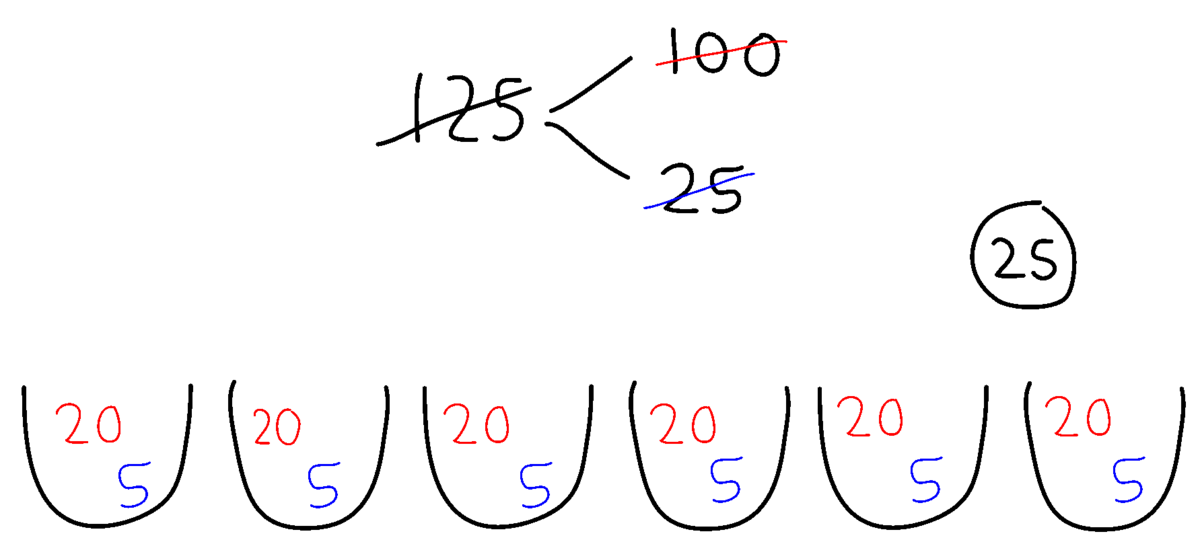
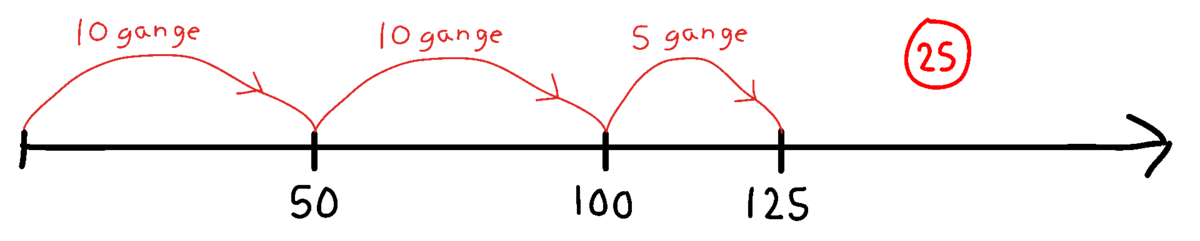
Tabellen herunder giver et overblik over de tre typer strategier med udgangspunkt i eksemplet $125 : 5$, og illustrationerne viser eksempler på, hvordan indirekte divison med en sekventiel strategi kan forbindes med tallinjen, og hvordan direkte division med en opdelingsstrategi kan forbindes med skålene.
I direkte division er udgangspunktet dividenden. I beregningen af 84 : 6 er der fx tale om direkte division, hvis en elev tænker, ’84 (vindruer) skal deles mellem 6 (personer)’, eller: ’Der er 84 borde. Jeg skal se, hvor mange gange jeg kan tage 6 fra 84.’'
I indirekte multiplikation er udgangspunktet divisoren. I beregningen af 84 : 6 er der fx tale om indirekte multiplikation, hvis en elev tænker: ’Jeg skal se, hvor mange gange 6 kan være i 84’.
I en sekventiel strategi er tænkningen baseret på gentagen subtraktion, hvis eleven bruger direkte division, og på gentagen addition, hvis eleven bruger indirekte multiplikation.
I en opdelingsstrategi er tænkningen baseret på opdelinger af dividenden.
En kompensationsstrategi involverer tilpasning af antallene og/eller beregningerne.
Fase 3
I fase 3 udvikler eleverne fortsat deres strategier til division, således at de efterhånden kan dividere mere og mere fleksibelt. Det implicerer, at de kommer til at råde over et repertoire af forskellige strategier, og at de i enhver beregning med division overvejer, hvilken af de strategier, de råder over, det vil være smartest for dem at vælge. Samtidig er det hensigten, at eleverne – efterhånden som de hver især er klar til det – skal udvikle måder at repræsentere deres tænkning på. De behøver fx ikke nødvendigvis at tegne tallinjer, selv om de stadig forestiller sig tallinjen, når de løser målingsproblemer.
Fase 3
At dividere flercifrede tal fleksibelt med støtte i tegninger og talsymboler.
Fase 4
I fase 4 er det idéen, at eleverne bliver opfordret til helt at slippe tallinjen og skålene, efterhånden som de ikke længere har brug for dem. Det betyder, at eleverne ’skubbes til’ gradvist at bruge regneudtryk og omskrivninger som støtte for deres tænkning. I den forbindelse er det vigtigt at være opmærksom på, at eleverne i en klasse næppe på samme tid er klar til et skifte fra at tænke med støtte i billedlige repræsentationer til at tænke med støtte i regneudtryk og omskrivninger. Skiftet bør komme, når den enkelte elev ikke længere har behov for de billedlige repræsentationer. På den anden side foretager den enkelte elev formentlig ikke et sådant skifte på eget initiativ. Der er behov for, at læreren introducerer regneudtryk som måder at symbolisere elevernes matematiske tænkning på. Eleverne må have mulighed for at skabe mening i regneudtrykkene og for selv at bruge sådanne måder at symbolisere dem på.
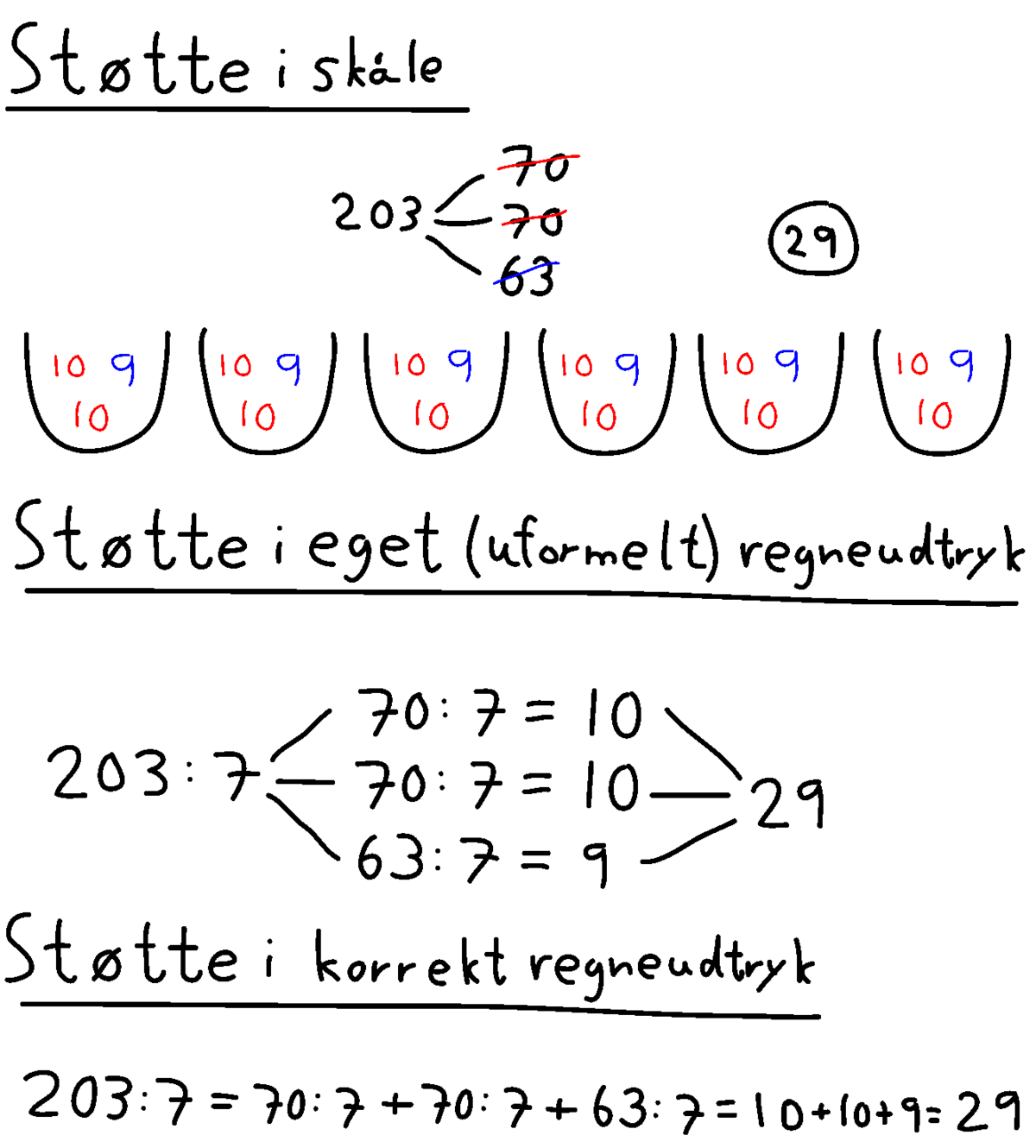
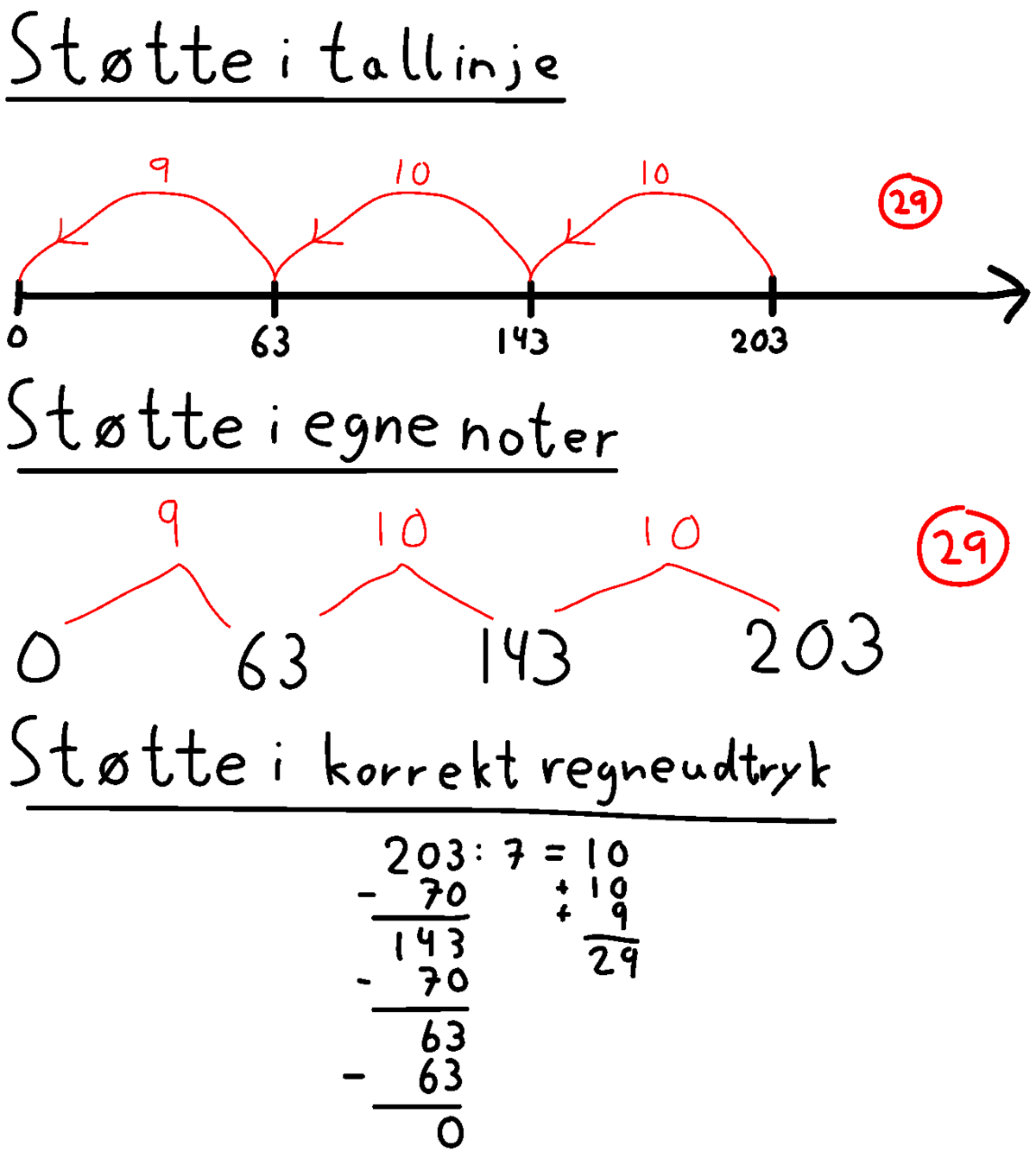
I begyndelsen kan elevernes regneudtryk fungere som en slags ’forlænget hukommelse’ for dem. De er ikke nødvendigvis sammenhængende og overholder ikke nødvendigvis formelle regler. Læreren kan guide eleverne til gradvist at skrive regneudtryk, der afspejler deres egen tænkning, og hvor de matematiske tegn er brugt rigtigt. De følgende to eksempler antyder, hvordan elevernes brug af ’skåle’ og tallinjer gradvist – med læreres støtte – kan udvikle sig til brug af regneudtryk.
Eksempel (203 : 7):
Eksempel (203 : 7):
Fase 4
At dividere flercifrede tal fleksibelt med støtte i regneudtryk.
Regneudtrykkene nederst i eksemplerne herover viser eksempler på såkaldte talbaserede metoder, der kan bruges i enhver division med flercifrede tal. Den ene metode skrives vandret. Den bygger på en opdelingsstrategi. Dividenden (203) opdeles i ’$10$ gange divisoren’ ($70$) så mange gange, det kan lade sig gøre.
Den anden metode skrives lodret. Den bygger på en sekventiel strategi. Der foretages så mange hop á ’$10$ gange divisoren’ ($70$), som det kan lade sig gøre.
Eksemplerne herover illustrerer, hvordan metoden med den vandrette skrivemåde er forbundet med ligedelingsdivision, og metoden med den lodrette skrivemåde er forbundet med målingsdivision. Efterhånden som en af metoderne bliver en del af elevernes repertoire af strategier til division, kan man dog opleve, at de forskellige måder at tænke division på ’smelter’ sammen, sådan at eleverne, afhængigt af problemstillingen, tænker målingsdivision og ligedelingsdivision sammen med begge repræsentationer og skrivemåder. På tilsvarende vis kan man opleve, at eleverne varierer mellem at tænke direkte og indirekte division i forbindelse med begge metoder.
I læringssporet er det hensigten, at enten den ene eller den anden metode kommer til at udgøre en del af elevernes repertoire af strategier. For læreren er det dog vigtigt at være opmærksom på, at metoden ikke fremstår som en opskrift, der er afrevet fra eleverne forståelse, men snarere som et produkt, der ligger i naturlig forlængelse af en sekventiel strategi eller en opdelingsstrategi.
En metode udgør ikke et afsluttende mål for læringssporet. Som tidligere beskrevet er målene derimod, at eleverne kommer til at dividere fleksibelt på grundlag af forståelse. Elever, der råder over et stort repertoire af strategier, de forstår, og som vælger en strategi, der er hensigtsmæssig for dem i et givent divisionsproblem, opfylder derfor i højere grad målene end en elev, der konsekvent vælger en bestemt metode.
Eksemplet til højre med divisionsstykket $203 : 7$ viser et regneudtryk, der bygger på en kompensationsstrategi.
Cifferbaserede metoder indgår ikke i læringssporet.
En metode til division er en på forhånd fastlagt strategi og skrivemåde, der kan bruges til division generelt.
I cifferbaserede metoder deler man fx 83 op i 8 og 3 uden at tænke på, at 8 repræsenterer antal tiere.
I talbaserede metoder ser man derimod på den værdi cifrene repræsenterer, fx ses 8 i 83 som 80 (Hickendorff et al., 2019).