Du er her: Forside Tal og algebra At anvende formler Praksis – At anvende formler

Praksis – At anvende formler

Afsnittet viser, hvordan læringssporet kan realiseres i praksis ved at give konkrete eksempler på, hvordan aktiviteterne i de fire faser kan iscenesættes og udføres. Det fremhæves, hvilke faglige pointer det er centralt at behandle undervejs og i opsamlingen, og hvordan man som lærer kan støtte elevernes fælles læring i klassen for at realisere sporets læringsmål. Som gennemgående eksempel arbejdes der med begreber inden for byggeri, men idéerne kan direkte overføres til andre erhvervsfaglige områder. Når man vælger emne, er det naturligvis vigtigt, at det indeholder en del formler til beregning af forskellige størrelser.

De tidsmæssige rammer

Undervisningsforløbet er beregnet til at vare 4-6 timer. Man kan vælge at bygge flere af sine forløb op på samme måde.

Faglige forudsætninger

Det forudsættes, at eleverne har mødt formler i folkeskolen, f.eks. formlen til at beregne arealet af en trekant eller formlen for omkredsen af en cirkel. Eleverne har oplevet formler i matematikundervisningen, men det er langt fra sikkert, at viden om formler er velfunderet hos alle elever. Tværtimod kan der være få – eller ingen – af eleverne på et hold, der sikkert kan vælge mellem flere formler, og som kan beregne korrekt med formlerne. Og måske endnu vigtigere så er det nok de færreste elever, der har et bevidst forhold til formler eller strategier for, hvordan man kan arbejde med at forstå en formel.  

Det forudsættes også, at eleverne kender nogle enkelte enheder for længde (f.eks. cm, m og km), vægt (f.eks. g og kg) og rumfang (f.eks. ml, liter, m3), samt at eleverne har prøvet at regne med og omregne mellem sådanne enheder. Man må dog forvente, at mange elever ikke har opnået sikkerhed i at regne med forskellige enheder og omregne mellem dem.

Fase 1

At afdække elevernes forudsætninger og viden

Undervisningen starter med et fokus rettet mod elevernes forforståelse. Eleverne skal aktivere deres matematiske viden fra grundskolen. Lærerens rolle er at aktivere og introducere så mange forståelser, eksempler og repræsentationer som muligt. Denne aktivering foregår ved, at eleverne i deres eget sprog forklarer, tegner og giver eksempler på formler, elementerne i dem, og hvor de bruges.

Vendekort med førfaglige ord

Som en forberedelse til undervisningen kan man som lærer finde 10 førfaglige ord, som man bruger i sin undervisning om et bestemt matematikfagligt ord eller begreb, og som man har erfaring med, at eleverne ikke kender, eller som de har en skæv forståelse af eller måske ligefrem misforstår. Det kan f.eks. være 'fortynde', 'svingning', 'balance', 'runde af', 'positiv' el.lign.

Lav nu vendekort på karton. På kortene skrives matematiske førfaglige ord.

I tilfældige grupper af 3-4 skal eleverne vende et kort og f.eks.:

  1. prøve at forklare, hvad det førfaglige ord betyder, uden at sige selve ordet, men med et eksempel på, hvornår og hvordan det bruges i praksis. Denne praksis kan enten være hentet fra erhvervsuddannelsen eller fra hverdagslivet.

  2. prøve at komme med et eksempel på, hvornår og hvordan ordet bruges i matematik.

  3. vende to kort og (hvis det er muligt) forklare, hvordan de har noget med hinanden at gøre. 

Formålet er at aktivere og udvide elevernes forforståelse for bestemte ord og begreber.

Elevernes forståelser, associationer, eksempler etc. kan fællesgøres i klassen ved hjælp af ’isbjergmodellen’ på tavlen, hvor læreren skriver ord over vandoverfladen. Eleverne udfylder isbjergmodellen under vandoverfladen med alle deres forståelser, associationer og eksempler. Dernæst strukturerer læreren indholdet ved at kategorisere elevernes input efter, om det er praktiske eksempler, beregningseksempler eller repræsentationer (grafer, geometriske konstruktioner og lignende). Læs mere om Isbjergmodellen i afsnittet Grundlag.

Ordkendskabskort

Fagord er en anden slags ord end førfaglige ord. Fagord har en specifik og defineret betydning i matematik.

Her skal eleverne i tilfældige grupper af 2-3 fremstille ordkendskabskort for et givet begreb, der skal indeholde følgende: definition, eksempel, undtagelse (det er ikke…), evt. formel og association.

Ordkendskabskortene hænges op i klassen til gallerivandring. Man skal ikke præsentere sine kort – i stedet skal alle elever gå rundt i 10 minutter og læse og diskutere de andre elevers kort. På baggrund af diskussionen laver grupperne en ny version af deres kort, eller eleverne laver individuelle noter.

Som afslutning på fase 1 kan man tage isbjergmodellen op igen og få skrevet flere ting på, som eleverne har fundet frem til i de seneste aktiviteter.

Fase 2

At genkende og gøre rede for formler og de størrelser og enheder, der indgår i dem

Denne fase bygger videre på de koblinger og associationer, som eleverne har lavet i fase 1, og her bliver fokus yderligere rettet mod formler. I undervisningen lægges der vægt på at genkende og gøre rede for formlerne og de symboler, der indgår i dem, og deres enheder.

Man kan evt. anvende begrebskort, hvor nogle af kortene indeholder formler og størrelser fra formler.

Et eksempel fra sygeplejeuddannelsen på et isbjerg over begrebet ’styrke’ (Møller & Tørring, 2022).

Begrebskort

Eleverne får i grupper af 3 udleveret en stak begrebskort med ord og begreber hentet fra matematikken, erhvervsuddannelsen og fra hverdagen og skal forklare, hvad der er på kortet, og hvordan kortene passer sammen. Det kan f.eks. give anledning til følgende sætninger, hvor ordene fra kortene er angivet i [ ] :

"[Bredden] skal man have for at kunne beregne [Areal]" eller "[Højden] er den stiplede linje på [tegningen af trekanten]". Det er vigtigt allerede her at få inddraget formler. Her kunne en forklaring være: "Der er [½] i formlen, for når man finder [Areal] af en trekant, er det halvdelen af en firkant".

Forklaringerne på sammenhængene kan nogle gange blive lidt kluntede eller søgte – det er okay. Det vigtigste er, at eleverne gør sig umage for at finde sammenhænge og forklaringer på sammenhænge.

Man kan også arbejde videre med ordkendskabskortene fra fase 1, hvor der igen er større fokus på formlerne og på, hvordan man fx kan omforme dem. I eksemplet på billedet har læreren valgt nogle kategorier ud fra elevernes input fra tidligere.

Det kan føre til en diskussion af formlen for arealet af en trekant. Læreren kan stille spørgsmål som:

  • Hvilke størrelser indgår i formlen? Hvad står bogstaverne for?

  • Hvilke enheder har de forskellige størrelser?

  • Hvad for nogle kan variere? Og hvilke er konstante?

  • Hvordan vil trekanten se ud, hvis man holder $b$ konstant?

  • Hvis man kender højden og arealet, hvordan regner man så bredden (eller grundlinjen) ud?

  • Hvad sker der med arealet af trekanten, hvis vi gør højden dobbelt så stor?

Nogle elever vil være glade for, at der bruges tal undervejs, men målet er, at eleverne bliver trygge ved formeludtrykket.

Fase 3

At fortolke og forklare formler fra erhvervsfag og matematik og at koble formler til andre repræsentationer af de samme sammenhænge

I denne fase handler det om koblingen til andre af erhvervsuddannelsernes repræsentationer. I undervisningen arbejdes der med at tolke og forklare forskellige typer repræsentationer af konkrete situationer. Repræsentationerne er på den ene side erhvervsfagets traditionelle repræsentationer af matematiske sammenhænge som maskinindstillinger, brugsanvisninger, sikkerhedsforskrifter, displays på maskiner eller apps, portaler og lign., der laver beregninger på basis af indtastede værdier, fx trekantberegnere. På den anden side kan der også være tale om matematiske repræsentationer: grafer, diagrammer, tabeller m.m. og selvfølgelig formler! Lærerens rolle er at støtte eleverne i at strukturere og formalisere deres forklaringer. I nogle tilfælde vil det være relevant at lade nogle elever selv prøve at opstille simple formler ud fra en konkret erhvervsfaglig situation.

Repræsentationerne er ’mellemstationer’ mellem problemet og løsningen, så elevernes fortolkning og forklaring på fx en graf kan være, hvordan man bruger den til løse et konkret problem. Man kan tolke grafen som et udtryk for en beregning, og man kan forklare, hvad grafen betyder for løsningen af et konkret problem. Nogle elever kan måske tolke grafen som en bestemt type formel.

Eleverne har brug for at kende og kunne bruge bestemte matematiske teknikker, såsom at lave ’sildeben’, tegne en graf og aflæse på den. Disse færdigheder bliver også trænet i denne fase. Man kan find inspiration til undervisningsmaterialer af denne type i grundskolebøger og på internettet, men forbindelsen til erhvervsuddannelseskonteksten må lærerne på EUD selv udvikle.

Tolke repræsentationer

Herunder gives et eksempel på, hvordan elever kan arbejde med at tolke repræsentationer. Eksempelt tager udgangspunkt i beregning af omdrejningstallet via en formel online, men det er op til eleverne selv at kunne fortolke og forklare de resultater, som computeren ender med at give.

At undersøge matematikken bag skærmen

www.fagteori.dk/beregn_omdrejningstallet.html

  • Lav en tabel, hvor du indsætter forskellige skærehastigheder og de tilhørende omdrejningstal. 

  • Vis derefter sammenhængen mellem skærehastighed og omdrejningstal med en graf.

  • Forklar grafen. Fx hvor meget stiger omdrejningstallet, når skærehastigheden stiger med…?

  • Kan man finde en formel, der beregner omdrejningstallet n for en diameter D?

Fremstille repræsentationer og generalisere ud fra dem

I denne aktivitet er der fokus på at udvikle elevernes forståelse af generalitet.

Lad eleverne lave grafer ud fra målinger, aflæsninger og eventuelt beregninger, fx af fortyndinger eller prisudviklinger. Disse repræsentationer afspejler en konkret situation, og det diskuterer man med eleverne. Herefter spørger man ind til, hvordan det vil se ud i andre men lignende situationer? Hvordan kan man generalisere ud fra en graf? Her vil udsagn fra eleverne som "Der sker det samme hver gang", eller "Det virker altid", eller "Hvis det fortsætter sådan, så sker det", indikere, at eleverne begynder at tænke generelt. Hvis muligheden viser sig, kan man inddrage formler, der kobler til en given graf, og diskutere, hvordan formlen er et udtryk for en generalisering. Man kan tage aktiviteten med at undersøge matematikken bag skærmen op igen og se på forskellige værdier af D. Hvordan beregnes omdrejningstallet generelt?

Opstille simpel formel fra en erhvervsfaglig situation

Figuren viser en tegning af en brændespand, som smede laver på deres grundforløb. Her kommer formler som omkreds, areal og rumfang godt i spil. Konkret handler det om at finde målene på de elementer, der skal klippes ud, og som tilsammen giver en brændespand.

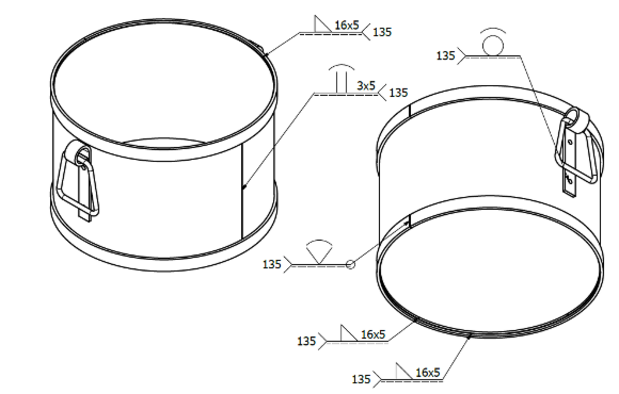
Man starter med at regne på målene fra arbejdstegningen. Man bruger færdige formler for cirklen (som bund) og den krumme overflade af en cylinder (som resten af spanden).

Herefter kan man tale med eleverne om, hvordan disse formler kan være opstået? Den krumme del kunne man jo klippe op og folde ud, så det giver et rektangel. Hvordan finder man arealet af det? Hvad er højden og bredde? Hele vejen igennem regner man på de kendte tal.

Med støtte kan nogle af eleverne måske selv opstille en formel for det samlede overfladeareal efter at have lavet beregninger på en brændespand med givne mål.

Man kan prøve at beskrive spandens overfladeareal, efter den er klippet op og foldet ud til et rektangel. Højden af rektanglet er den samme som højden af spanden, $h$, og bredden af rektanglet er det samme som omkredsen af spanden. Så hvis vi kender diameteren, $d$, bliver omkredsen $\pi \cdot d$, og så kan man finde arealet som $A_{cylinder} = h \cdot \pi \cdot d$. 

Figuren viser, hvordan man klipper en cylinder op, folder den ud og får et rektangel. Overfladearealet af cylinderen er det samme som arealet af rektanglet.

Nu har brændespanden jo en cirkulær bund, så man skal lægge arealet af en cirkel med diameter $d$ til. Bunden har arealet $A_{bund} = \pi \cdot \frac{d^2}{4}$. Hvis man vil regne arealet af hele brændespanden ud, skal de to arealer $A_{cylinder}$ og $A_{bund}$ lægges sammen, og så har man faktisk ’bygget’ en helt ny formel: 

$A_{spand} = h \cdot \pi \cdot d + \pi \cdot \frac{d^2}{4}$

Det er slet ikke alle elever, som vil kunne komme igennem de argumenter, der er gennemgået her, og så bruger man i stedet den færdige formel til beregning af materialeforbruget.

Fase 4

At anvende formler fleksibelt og med mening til problemløsning i forskellige sammenhænge

I denne fase drejer det sig om at bruge eksisterende formler. Eleverne skal opdage og løse problemer ved hjælp af de matematiske redskaber, som de har opbygget forståelse for i fase 1, 2 og 3. Lærerens rolle er at støtte og udfordre eleverne i at reflektere over, hvor de befinder sig i processen, og om hvorvidt resultaterne i de enkelte trin giver mening for dem. Herigennem opdager eleverne (forhåbentlig) også, at de formler, der kan bruges til at løse problemer, som ligner hinanden, også minder meget om hinanden.

Der er mange ting, man skal have styr på, for at anvende formler rigtigt, og det kan nemt gå galt. Man kan se eksempler på elever, der vælger den forkerte formel til en given situation, sætter forkerte tal ind, omformer forkert, opstiller formlerne forkert i forhold til en given kontekst, bruger forkerte enheder, misforstår resultatet osv. En af de ting, der kan gøre det svært at arbejde med formler, er, at man kan opfatte dem på flere helt forskellige måder. Typisk vil man i erhvervsuddannelserne bruge formler som en input-outputmaskine – en slags opskrift til at regne noget ud. Man indsætter tal på de forskellige symbolers pladser og regner resultatet ud. Men sommetider skal en formel opfattes som en ligning, hvor man godt nok stadigvæk skal sætte tal på symbolernes pladser, men nu er det nødvendigt at omforme udtrykket (rykke rundt på det), før man får isoleret den størrelse, der er brug for. Hvis man i trekantens arealformel kender grundlinje og areal, kan man finde højden ved at omforme formlen $A = \frac{1}{2} \cdot h \cdot g$ til $h = \frac{2 \cdot A}{g}$.

En anden måde at forstå formler på er som en tekst, man kan læse og forstå. Når man læser $A = \frac{1}{2} \cdot h \cdot g$, betyder det, at man kan ”se”, at det må være arealet af en trekant, fordi $h \cdot g$ jo er arealet af en firkant, og når vi kun tager halvdelen, må det være en trekant. I forbindelse med fx modellering opfattes formler sommetider som et blueprint – altså en slags arbejdstegning af det, man modellerer. Det kan være formlen for arealet af en husgavl, der består af et rektangel og en trekant, så man kan ”bygge” sin egen formel:

$A_{gavl} = h \cdot b + \frac{1}{2} \cdot h \cdot b$

Her skal man være opmærksom på, at sådanne formler ofte bygger på særlige forudsætninger, som her at ”højden” af rektanglet og trekanten er den samme.

En anden udfordring er, at eleverne kan komme til at identificere en formel med det begreb, som formlen henviser til. Fx vil nogle elever sige, at formlen $A = \frac{1}{2} \cdot h \cdot g$ ER en trekant i stedet for at opfatte formlen som en måde at beregne arealet af en trekant. Misforståelsen kan opstå, hvis eleverne – hver gang de hører om trekanter – ser eller bruger formlen for arealet.

Man kan møde en anden type misforståelse i forbindelse med formlen $A = \frac{1}{2} \cdot h \cdot g$; nemlig at det er arealet af en retvinklet trekant. Eleven har måske flere gange set, at formlen kommer fra opdelingen af et rektangel med bredden $g$ og højden $h$ i to trekanter langs diagonalen. Det giver jo netop to retvinklede trekanter, som hver har arealet $A = \frac{1}{2} \cdot h \cdot g$. For at komme den misopfattelse til livs kan man lave følgende figur med to parallelle linjer, der har afstanden $h$:

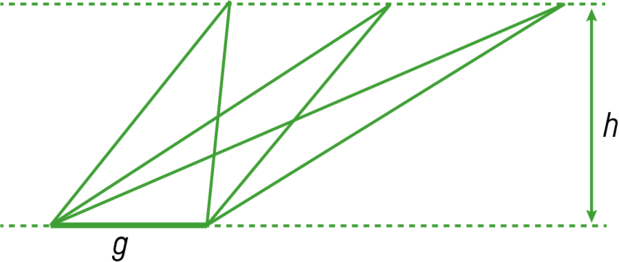
Dermed kan man vise, hvordan alle trekanter med den viste grundlinje og øverste vinkelspidst på den øverste linje må have samme areal $A = \frac{1}{2} \cdot h \cdot g$. De har jo samme grundlinje og samme højde, og så viser formlen, at de må have samme areal! Her ser man formlen som en sammenhæng mellem $h$ og $g$, og når ingen af dem ændrer sig, forbliver arealet også det samme.

Mange elever har faste meninger om, hvordan en bestemt formel skal se ud. Det er formlens udseende, der gør den til en særlig formel. Sommetider handler det om de bogstaver (symboler), man bruger. Når det drejer sig om funktioner, synes mange, at de variable skal hedde x og y. Hvis man i stedet bruger andre navne, kan elever have svært ved at genkende formlen. Et andet problem kan knytte sig til den rækkefølge, man skriver tingene op i. For eksempel vil nogle elever se arealformlen for en trekant skrevet på to forskellige måder $A = \frac{1}{2}h \cdot g$ og $A= \frac{h \cdot g}{2}$ som to forskellige formler – for er det nu også det samme at gange med $\frac{1}{2}$ og dividere med $2$? I undervisningen er det derfor en god idé at variere måden, man skriver tingene op på, og bruge forskellige symboler for den samme størrelse. Selvfølgelig er det også en pointe, at elever lærer de gældende konventioner for, hvilke symboler man bruger i forskellige kontekster. 

Der findes endnu flere forståelser af formler, og for at blive en god formelbruger er det nødvendigt, at man kan veksle mellem dem. Det står der mere om i afsnittet Grundlag. I de tidligere faser er der allerede blevet arbejdet med flere af forståelserne i aktiviteterne med begrebskortene og ordkendskabskort. I denne fase laver eleverne aktiviteter, hvor de skal bruge forskellige forståelser og veksle mellem dem.

For at bevare overblikket og kontakten mellem det erhvervsfaglige problem og matematikken arbejder eleverne i undervisningen med gradvis matematisering og modellering af situationer og problemer fra erhvervsuddannelsen, så de kan løses ved hjælp af formler.

1. Matematisering af et problem

Først skal problemet identificeres:

Hvis spæret er 20 cm højt med en hældning på 40 grader, hvor højt er så det lodrette snit ude for enden af spærudhænget? Hvor mange brædder skal der sidde på undersiden af spærudhænget?

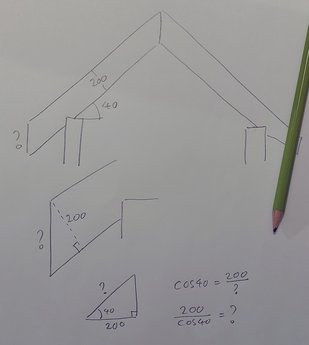
Derefter laver man en skitse med de oplysninger, man kender.

Gradvist identificerer og isolerer man den størrelse, der skal bestemmes, og udvælger den formel, der kan anvendes. I dette tilfælde har man en retvinklet trekant, hvor en vinkel og en katete er kendt, og hvor man skal bestemme hypotenusen – så kan cosinus bruges.

Resultatet bliver 261 mm, og det stemmer godt overens med de øvrige mål. Tallet skal være (lidt) større end bredden på spærplanken på 200 mm. Hvis det er muligt, kan man afprøve resultatet i praksis.

Hele processen kan skrives op i punktform:

  1. Formuler problemet.
  2. Lav en skitse.
    1. Her sker en idealisering og strukturering af problemet.
  3. Lav et diagram.
    1. Dvs. der tilføjes enheder og værdier til de dele af skitsen, man kender. Desuden skrives ’x’ eller ’?’ ved de længder, vinkler, værdier, man ikke kender.
  4. Udvælg korrekt formel.
  5. Oversæt fra diagram til formel ved at indsætte kendte værdier fra skitsen i formlen.
  6. Beregn.
  7. Valider resultatet.
    1. Dels valideres slutresultatets størrelse (hav fokus på elever, der fx siger: ”Lommeregneren skriver, at den håndvask skal være 16 m2 stor”!).
    2. Dels valideres den relevante nøjagtighed (hav fokus på elever, der siger: ”Vi skal bruge 3,401246 meter lægte”).
    3. Dels valideres den relevante enhed (hav fokus på elever, der fx skriver, at man har 4.386.700 kubikmillimeter sand).
  8. Implementer.
    1. Hvis det er muligt at prøve resultatet af i praksis, er der ikke noget så tilfredsstillende som at få bekræftet, at beregninger, opmærkning og tilskæring faktisk passer i praksis.
    2. Der er også god læring i at vurdere omfang og konsekvens af (manglende) præcision i forhold til erhvervsfaglige standarder.

I de næste aktiviteter arbejder eleverne med de forskellige forståelser af formler.

2. En formel forstået som en opskrift

Hvis man sætter ’de rigtige’ værdier ind i stedet for bogstaverne, får man ’det rigtige’ resultat ud i den anden ende. Denne forståelse relaterer til lighedstegnet som en ’operator’ – altså som noget, man skal gøre.

Man vælger en erhvervsfaglig situation, som de studerende kender, og som kan beskrives med en formel, samt passende mål, der skal sættes ind.

Målene med denne aktivitet er, at eleverne skal lære:

  • at identificere de rigtige værdier i en problemstilling (er trekanten 25 cm bred eller 25 cm høj?)
  • at udvælge den rigtige formel
  • at koble talværdien med en enhed (er enheden 10 meter, sekunder eller m/s?)
  • at indsætte tallene på rette sted i formlen
  • at vælge og bruge hjælpemidler hensigtsmæssigt
  • at vurdere beregningsresultatet matematisk (er der regnet rigtigt?)
  • at vurdere beregningsresultatet som en hensigtsmæssig løsning i forhold til problemet
  • evt. at bruge enheder som en støtte til at vurdere resultatet
  • at opstille et eksperiment eller en handling, der kan validere resultatet (kan det være rigtigt, at arealet af håndvasken er 16,5 m2?)

Her gives nogle aktiviteter, der kan udfordre eleven og vise, at formler kan forstås på andre måder end en opskrift:

3. Formler forstået som blueprint

I fase 3 arbejdede eleverne fx med en brændespand. I den proces, hvor man opstiller en formel for det samlede overfladeareal, ser man formlen som et blueprint – altså som en anvisning af, ’hvordan man gør’. I aktiviteten fra fase 3 er argumenterne for at kunne opstille en formel for brændespandens overfladeareal $A_{spand} = h \cdot \pi \cdot d + \pi \cdot \frac{d^2}{4}$ gennemgået.

4. At arbejde med en formel som en ligning

Ligninger er matematiske udtryk med et ’$=$’, der kan omformes ved hjælp af nogle bestemte regler. Fx kan man gange med det samme tal eller det samme udtryk på begge sider af lighedstegnet.

Aktiviteter, der understøtter denne forståelse, hører egentlig ikke til i dette læringsspor, da det hører under emnet ’omformning af ligninger’. Her kommer alligevel et eksempel på, hvordan man kan arbejde med omformninger af formler.

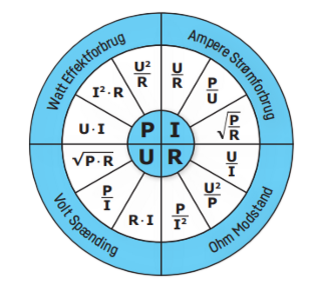
Elektrikernes Effekthjul er et godt eksempel på, hvordan formler skrives i erhvervsuddannelser, og hvordan man kan arbejde med sammenhængen mellem formlerne vha. omformninger, dvs. hvor formlerne forstås som ligninger.

Man kan komme fra formlen for effekt til formlen for spænding ved følgende omformninger, der alle kan findes i effekthjulet:

$\textbf{P} = \textbf{U} \cdot \textbf{I} \Leftrightarrow \frac{\textbf{P}}{\textbf{I}} = \frac{\textbf{U} \cdot \textbf{I}}{\textbf{I}} \Leftrightarrow \frac{\textbf{P}}{\textbf{I}} = \textbf{U}$

  • Prøv at vise, hvorfor $\textbf{R} = \frac{\textbf{U}^2}{\textbf{P}}$
  • Prøv at vise, hvorfor $\textbf{U} = \sqrt{\textbf{P} \cdot \textbf{R}}$
  • Prøv at vise, hvorfor $\textbf{I} = \sqrt{\frac{\textbf{P}}{\textbf{R}}}$
  • Prøv at vise, hvorfor $\textbf{P} = \textbf{I}^2 \cdot \textbf{R}$
  • Hvad sker der med $\textbf{P}$, når $\textbf{R}$ bliver dobblet så stor? 3 gange så stor?

I det sidste spørgsmål skal man forstå formlen som en relation mellem to variable, P og R, lidt som om den var en funktion.

Elektrikerens Effekthjul.

5. At skifte fleksibelt mellem forståelserne

Den sidste aktivitet involverer flere forskellige opfattelser eller forståelser af formler. For at kunne lave opgaverne er det derfor vigtigt, at man kan skifte fleksibelt mellem dem. Det ene øjeblik skal man kunne læse mening ind i formlen, som om den var en tekst; det næste skal man kunne sætte tal ind, som var den en input-outputmaskine; så skal man skrive om på udtrykket, som om den var en ligning; og måske skal man også kunne sige noget om, hvordan de variable i formlen ændrer sig sammen, som om formlen beskrev en relation.

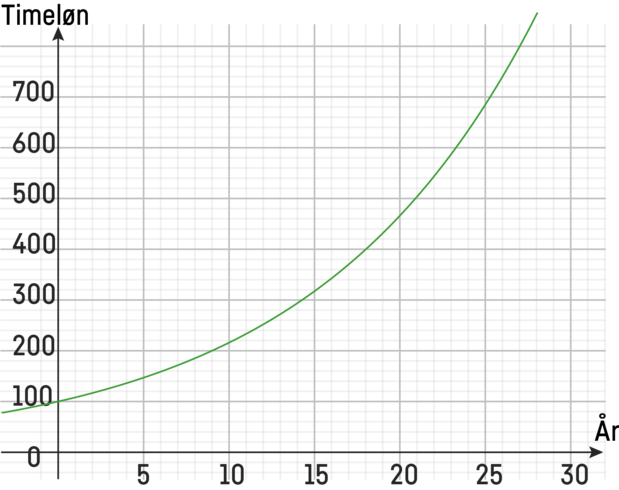
Figuren viser en model for, hvordan prisen for en håndværkertime i byggeriet kan antages at have udviklet sig over de senest tre årtier, hvor $L$ er timelønnen og $t$ er antallet af år, der er gået.

Efter hvert spørgsmål skal du prøve at sætte ord på, hvordan du har brugt formlen:

$L = 100 \cdot (1 + 0,08)^t$

  1. Hvor mange procent stiger timelønnen hvert år?
  2. Hvad er timelønnen efter 5 år?
  3. Forklar, hvorfor grafen stiger mere og mere pr. år. Prøv at se på formlen, eller vis det med nogle beregninger.
  4. Hvor mange år går der, før din timeløn er fordoblet? Løs gerne på flere måder.
  5. Hvornår vil timelønnen være 1400 kr. ifølge modellen? Er det realistisk?
Revideret 02.04.2025
-
Clemens Merker