Grundlag – At anvende formler

Forståelsen af algebra og formler

Formler er færdiglavede 'opskrifter' skrevet i matematikkens sprog som generelle sammenhænge. Formler er en fast del af alle fags ’værktøjskasse’ til at løse problemer.

Problemerne med brugen af formler i undervisningen og i erhvervsfagene kan bestå i, at elever vælger den forkerte formel til en given situation, sætter forkerte tal ind, omformer forkert eller opstiller formlerne forkert i forhold til en given kontekst (Kieran, 1992).

Når man arbejder med symbolske udtryk, kan der være mange ting på spil. Der er for eksempel stor forskel på følgende to situationer, hvor man ser på udtrykket for arealet af en cirkel $A=\pi \cdot r^2$. I den ene slags situation 1) kender man værdien af $r$, som indsættes, hvorefter man beregner $A$. I den anden slags situation 2) kender man arealet $A$ og skal bestemme, hvilken radius $r$ der så er i cirklen.

Ifølge Janvier (1996) er det i den første slags situation, at udtrykket for cirklens areal er en formel. Han definerer: En formel er to symbolske udtryk forbundet med et ”=”-tegn, der kun kræver direkte beregninger med kendte tal – altså hvor man sætter ind og regner ud.

Bruger man derimod udtrykket $A=\pi \cdot r^2$ som i situation 2), er det i stedet en ligning, for her skal der først en omformning til, dvs. man regner på ukendte tal, før radius kan bestemmes ved direkte beregninger. Forskningen viser, at denne situation er meget sværere for eleverne. I Janviers definition er det er altså afgørende, hvad man gør ved det symbolske udtryk, for at det opfylder kravet til at være som en formel. 

Et andet bud på en mere operationel definition findes i Schou og Bikner-Ahsbahs (2022), der giver en noget bredere definition af en formel, som tager hensyn til, at formler kan opfattes og behandles på forskellige måder:

En formel består af to symbolske udtryk forbundet med et ”=”-tegn, der udtrykker, at noget er ens i en given kontekst. Nogle af de algebraiske symboler refererer til mål, som stammer fra denne kontekst, og de kan enten være faste eller variable og enten kendte eller ukendte.

Her skal man bemærke ordet ”kontekst”. Med denne definition er et regneudtryk en formel, når den refererer til noget i denne kontekst. Konteksten kan være en konkret situation på byggepladsen, hvor elementerne i formlen f.eks. kan referere til nogle afstande, der skal måles op, til en geometrisk illustration af f.eks. en cirkel eller til tænkte situationer om fx økonomi.

I Schou og Bikner-Ahsbahs definition lægges vægt på, at en formel er et udtryk for en sammenhæng i en kontekst. Denne forståelse for formler er valgt i dette læringsspor, da det arbejder med, at eleverne både skal forstå de matematiske sammenhænge og de konkrete kontekster. Undervisningen har som mål, at formlerne skal være et redskab til at danne bro mellem disse to verdener.

I arbejdet med formler kan eleverne have forskellige opfattelser af formler:

En formel kan være en opskrift. Hvis man sætter de rigtige værdier ind i stedet for bogstaverne, får man det rigtige resultat ud i den anden ende. Denne forståelse relaterer til lighedstegnet som en ’operator’.

En formel kan være en ligning. Ligninger er matematiske udtryk, der kan omformes ved hjælp af nogle bestemte regler. F.eks. kan man gange med det samme udtryk på begge sider af lighedstegnet. Hvis man multiplicerer ligningen $A = \frac{1}{2}hb$ med 2 på begge sider $2 \cdot A = 2 \cdot \frac{1}{2} \cdot h \cdot b = h \cdot b$, er ligningen stadig sand. 

Når man isolerer en bestemt variabel i en formel, kan der være tidspunkter, hvor formlerne nok er sande uden nødvendigvis at være meningsfulde. Det betyder, at man foretager regneoperationer, uden at resultatet kan valideres i forhold til konteksten. Det er ikke til at vide, om de enkelte mellemregninger er rigtige i forhold til det foreliggende problem. Man må stole på, at de er rigtige i forhold til de algebraiske regneregler.

En formel kan være en relation. Hvis $P = U \cdot I$, så er $2 \cdot P=2 \cdot U \cdot I$. Denne opfattelse relaterer til forståelsen af lighedstegnet som et udtryk for ’balance’. Det, der står på den ene side, er det samme som det, der står på den anden side. Hvis begge sider bliver dobbelt så store, balancerer relationen stadigvæk. Hvis $P$ bliver dobbelt så stor, så bliver $U$ det også, hvis $I$ ikke ændrer sig.

En formel kan være et blueprint. Det vil sige som en anvisning af, ’hvordan man gør’. F.eks. skal du ’bare’ tage radius og gange med $2$ og gange med $\pi$, så har du omkredsen af en cirkel.

En formel kan opfattes som en identitet. Elever kan opfatte, at $A$ i formlen $A = \frac{1}{2} \cdot h \cdot g$ er arealet (selve trekanten). Det er faktisk ikke arealet, men en måde blandt flere at beregne størrelsen af arealet på. 

En formel kan opfattes som at have et bestemt udseende. Den opfattelse kan komme til udtryk, hvis eleverne opfatter $A = \frac{1}{2} \cdot h \cdot b$ eller $ A = h \cdot \frac{1}{2} \cdot b$ eller $\frac{1}{2} \cdot h \cdot b = A$ som tre forskellige formler (Schou og Bikner‑Ahsbahs, 2022).

En vigtig skelnen:

• På den ene side kan man omforme en formel. Det er det, man gør, når man bruger de grundlæggende regneregler, fx for at isolere et bestemt led i formlen. Det kaldes også at manipulere formlen.
• På den anden side kan man lave om på en formel. Formlen for rumfanget af en prisme er volumen = grundflade gange højde. Med symboler er formlen $V = G \cdot H$. Denne formel kan laves om, så $G$ for grundflade erstattes med et andet udtryk. Hvis grundfladen er en trekant, kan man skrive $\frac{1}{2} \cdot h \cdot g$ i stedet for $G$. Så ser formlen for rumfang sådan ud: $V = \frac{1}{2} \cdot h \cdot g \cdot H$.
  Bemærk, at der både indgår et stort $H$ og et lille $h$. Det er fordi, der både er en højde ($H$) i prismet og en højde ($h$) i trekanten. At læse formlen kræver forståelse for, hvad de enkelte dele af formlen betyder, og lige her skal man passe særligt på! 

Algebraisk tænkning

Det er ikke algebraisk tænkning at udregne $2 \cdot 11=\text{__}$. Det er ikke algebraisk tænkning at gange med $2 \cdot 11$ på begge sider af lighedstegnet i udtrykket $\frac{14}{2 \cdot 11} = x$. Det er heller ikke algebraisk tænkning at sætte værdier ind i en formel for at få et resultat, f.eks. at indsætte $r = 8$ i formlen $r^2 \cdot \pi = A$ for at få resultatet $201$. Det kræver ikke algebraisk tænkning, men en anden slags tænkning; nemlig kendskab til værdier og enheder, hvor man kan tænke over ’Hvad betyder $r$?’ og ’Hvilken værdi har $\pi$?’.

Derimod har algebraisk tænkning et fokus på brugen af regneregler samt at kunne regne med ubekendte. Når man fx dividerer med $r^2$ på begge sider af lighedstegnet i udtrykket for cirklens areal, så man får en ny formel, der fortæller, hvordan man bestemmer værdien af $\pi$, så er det et eksempel på algebraisk tænkning. Her foretager man en regneoperation (at dividere med $r^2$ på begge sider) uden at nå frem til et resultat, der kan valideres i forhold til den meningsfulde opgave. Dette kaldes for evnen til at kunne rumme ’mangel på meningsfuld afslutning’ (på engelsk: acceptance of ‘Lack of Closure (ALC)’ (Janvier, 1996)). Man har altså evnen til at kunne rumme og håndtere beregninger, hvor man ikke kan vide, om de enkelte trin er rigtige og giver mening i forhold til det foreliggende problem. Man må stole på, at mellemregningerne er rigtige i forhold til de algebraiske regneregler.

Den matematiske diskurs

Dette læringsspor er baseret i et fagsyn om, at matematik er en social konstruktion.

I dette fagsyn eksisterer matematiske begreber ikke ’i sig selv’, men kun som 'aftaler' mellem mennesker, kaldet en diskurs. At kunne matematik er at kunne begå sig i denne særlige diskurs.

Diskursen består af 3 dele:

1. Særlig terminologi: veldefinerede fagord og begreber 
2. Visuelle hjælpemidler: talsymboler, tegninger, grafer, tabeller, symboler
3. Endorsed narratives – altså accepterede matematiske fortællinger: teoribygninger, definitioner, aksiomer, beviser, men også lokale resultater af matematisk aktivitet

I afsnittet om sproglighed omtales dette som ’efter-faglige’ ord og modeller, hvor eleverne efter en undersøgelse og italesættelse udvikler egne forklaringer og begreber, som alle involverede forstår og kan bruge.

Ifølge Anna Sfard (2008) er et hovedformål med matematik at producere narrativer: fortællinger og forklaringer, der kan blive accepterede og anerkendte som værende sande: ”The overall goal of mathematizing is to produce narratives that can be endorsed, labeled as true, and become known as ‘mathematical facts’”.

4. Derudover består en diskurs også af ’rutiner’, dvs. etablerede metoder til at behandle problemer, kaldet objekt-rutiner, og rutiner i, hvordan man ræsonnerer og begrunder med matematik. Det kalder man meta-rutiner.

Nu kan eleverne ikke bare blive enige om, at $2 + 2 = 5$. Deres fortællinger skal også afstemmes med de allerede anerkendte matematiske fortællinger, der f.eks. står i formelsamlinger og opslagsværker. Pointen er, at eleverne først udvikler deres egen forståelse og derefter anerkender de fælles forklaringer som værende ’også sande’. Lærerens rolle er at repræsentere den etablerede matematik og samtidig anerkende elevernes forståelse som værende ’også valide’ som udtryk for elevernes forståelse.

Begrebsdefinition og begrebsbilleder

David Tall og Shlomo Vinner (1981) har udviklet en teori om, hvordan elever udvikler forståelse for matematiske begreber. Deres teori bygger på den konstruktivistiske idé om, at viden ikke modtages passivt, men opbygges aktivt af det enkelte individ. I deres teori indfører de ’kognitive begrebsbilleder’, der er elevens samlede sum af beskrivelser og forestillinger til et givet matematisk begreb. Disse indre mentale billeder indeholder erfaringer og associationer til processer, repræsentationer og viden om egenskaber ved begrebet. En elev kan f.eks. have erfaringer med begrebet multiplikation fra matematikbogen i folkeskolen, fra materialekalkulation, fra tasterne på en lommeregner, lægning af fliser eller tagsten og eventuelt fra situationer, hvor der skulle multipliceres med tal mindre end 1 eller med negative tal. Nogle af begrebsbillederne kan være forkerte eller mangelfulde, men det samlede kognitive matematiske begrebsbillede vil udvikle og ændre sig, efterhånden som eleven arbejder med begrebet multiplikation i undervisningen.

Hvis man beder elever om at forklare begrebet multiplikation, vil de fleste komme med nogle subjektive forklaringer, tegninger eller eksempler på udregninger. Disse betegnes som personlige begrebsdefinitioner.

Når et større antal personer bliver enige om en bestemt samlet fælles definition af et begreb, kaldes det for en formel begrebsdefinition. Det er f.eks. de formler og forklaringer, man kan finde i formelsamlinger og matematikbøger. Man kan benytte begrebskort til at udvikle elevernes begrebsbilleder (Højgaard & Johansen, 2022).

Begrebskort og ordkendskabskort hjælper elever med at blive opmærksomme på nye begrebers betydninger. Det er nødvendigt, at eleverne får lov til at beskrive og forklare begreberne med egne og førfaglige ord (Weeks et al., 2013).

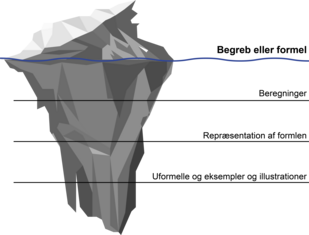
Elevernes begrebsbilleder kan så italesættes, struktureres og fællesgøres, så de forskellige begrebsbilleder kan sammenlignes, udfordres og generaliseres henimod den formelle begrebsdefinition. Et godt redskab til denne struktureringsproces er Isbjergmodellen.

Isbjergmodellen

Isbjergmodellen er en metafor for, at der ligger meget forståelse bag – eller under – et formelt begreb. Idéen bag modellen er, at en god, robust forståelse af begrebet bygger på et solidt fundament af viden, erfaringer og associationer, som udgør den del af isbjerget, der ligger under vandoverfladen. Dette fundament kan have forskellige udtryk og være mere eller mindre formelt; det kan være eksempler, citater, forklaringer, tegninger, diagrammer eller enheder, der hører til begrebet.

Isbjergmodellen kan anvendes som værktøj til at sikre, at eleverne får mulighed for at trække på deres egne erfaringer (Webb, Boswinkel og Dekker, 2008).