Tilgang – At anvende formler
Tilgangen i dette læringsspor er, at eleverne skal arbejde med at skabe forbindelser mellem deres intuitive forståelse af erhvervsfaglige fænomener på den ene side og på den anden side brugen af matematiske beregninger og formler, som anvendes i sådanne sammenhænge. Eleverne skal opdage, undersøge og beskrive konkrete situationer for gradvist at kunne strukturere og sammenfatte deres viden, så de kan forstå og anvende formler i relation til sådanne situationer.
Relationer og koblinger
At forstå noget er at kunne sætte ord på og at have associationer og repræsentationer knyttet til fænomenet. Når det gælder en formel, drejer det sig om at kunne læse mening ind i den ved at sætte formlen og de størrelser, der indgår i den, meningsfuldt i relation til noget andet. På erhvervsuddannelserne er det i høj grad i relation til noget uden for matematikken. På erhvervsuddannelserne er eleverne også motiverede for at koble deres skolelæring specifikt til deres valgte erhvervsfaglighed. Læreren kan derfor med fordel bruge elementer hentet fra erhvervsuddannelsen og lægge vægt på koblinger mellem disse elementer og matematikken.
Eksempel på oplæg til dialog om koblinger mellem omverden og matematik
”Vil det være meningsfuldt at bruge formlen for rumfanget af en cylinder til at beregne rumfanget af en træstamme? Den er jo tykkere i den ene ende end i den anden.” (kobling nr. 1)
”Måske kunne man bruge gennemsnittet af arealet i toppen og arealet i bunden af træstammen? Eller man kunne måle omkredsen på midten af stammen?" (kobling nr. 2)
En træstamme, som er skåret af i begge ender, er vel det samme som en keglestub? Det er der formler for.” (kobling nr. 3)
”Gad vide, om de forskellige beregninger, hvor vi bruger forskellige formler – cylinderen med gennemsnitsdiameter og keglestubben – vil føre til samme resultat?”
På denne måde kan man lægge op til en matematisk undersøgelse, der har en tæt forbindelse til den konkrete problemstilling.

Undervisningen i dette læringsspor baserer sig på Piagets teori om, at forståelse er at have opbygget et ’skema’. Tilgangen i undervisningen er at afdække elevernes skema, så eleverne får mulighed for at strukturere elementerne i skemaet og at kvalificere skemaet. Det gør man dels ved at tilføje flere teknikker, processer, erfaringer og repræsentationer til skemaets delelementer og dels ved at forbinde elementerne i skemaet, så eleverne bliver bedre til at vurdere og anvende det, som skemaet handler om – i dette tilfælde gælder det formler.
Det samlede skema for forståelse af et matematisk begreb består både af elementer i skemaet og forbindelserne mellem dem. Teknisk indsigt og færdighed i at beregne resultater er to af mange elementer, der indgår i skemaet. Et eksempel er forståelse for, at en graf kan udtrykke den samme sammenhæng mellem størrelser, som en formel kan, så det er vigtigt at etablere forbindelsen mellem elementerne ’graf’ og ’beregningsresultat’. Hvis formlen bruges som en funktion af én variabel, kan vi ud fra grafen finde de resultater, som vi ellers ville have brugt formlen til at beregne i det interval, grafen dækker.
For at finde ud af, hvad eleverne ved, kan og forstår omkring formler i almindelighed og en given formel i særdeleshed, kan man benytte forskellige aktiviteter, der kan give både lærer og elever relevant indsigt i, hvad eleverne ved om formler.
Det mest simple er at bede eleverne om at komme med frie associationer til en matematisk formel. Det kan fx være formlen
$A = \frac{1}{2} \cdot h \cdot b$,
som de allerfleste nok kan genkende. Det vil nok give en række ord og måske også nogle erfaringer med brug af formlen. Dem kan man så supplere med relevante ord og begreber, som læreren ønsker inddraget.
Det er et selvstændigt formål med øvelsen at få eleverne til at flytte deres fokus fra selve formlen og beregning af en trekants areal til at se på, hvilke begreber der indgår i eller har forbindelse til formlen. Det næste skridt er derfor at fokusere på forbindelserne imellem de forskellige begreber, der er kommet på tavlen. Det sker ikke af sig selv, men kan støttes, ved at læreren udvælger 5-10 begreber og skriver dem på et ’begrebskort’. Derefter bliver eleverne bedt om at beskrive, hvordan begreberne kan forbindes med en sætning.
Læreren kan støtte elevernes arbejde med at finde associationer og samtidig undersøge elevernes forståelse af et begreb ved fx at spørge:
- Kan du komme med et eksempel?
- Hvor bruger man den?
- Hvornår har du brugt den formel?
- Hvordan bruger man den formel?
- Hvordan kan det se ud?
- Hvad betyder de enkelte bogstaver?
- Hvilke enheder bruger man?
Den omvendte tilgang er ’ordkendskabskort’, hvor forbindelserne er givet på forhånd. Læreren skriver formlen, det drejer sig om, op i midten – her er det arealformlen for en trekant. Udenom skrives forskellige kategorier, der har forbindelse til formlen, fx eksempler, definitioner, egenskaber, modsætninger, undtagelser, repræsentationer osv. Her er valgt ’Det er ikke…’, ’Hvad er det?’, ’Hvor kan man bruge den?’ og ’Egenskaber’. Læreren kan på forhånd have lavet kort med mulige svar på, eller man kan lade eleverne selv udfylde tomme kort, som de derefter placerer under de rigtige kategorier.
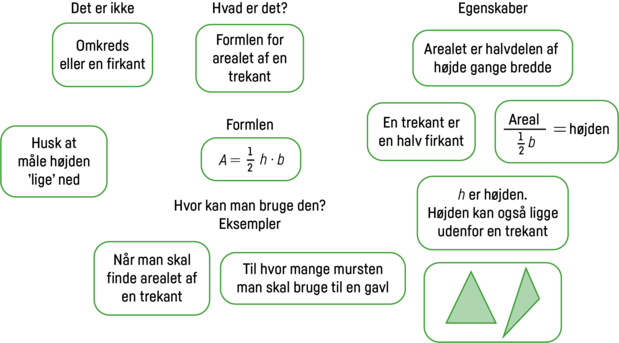
Endnu et ordkendskabskort
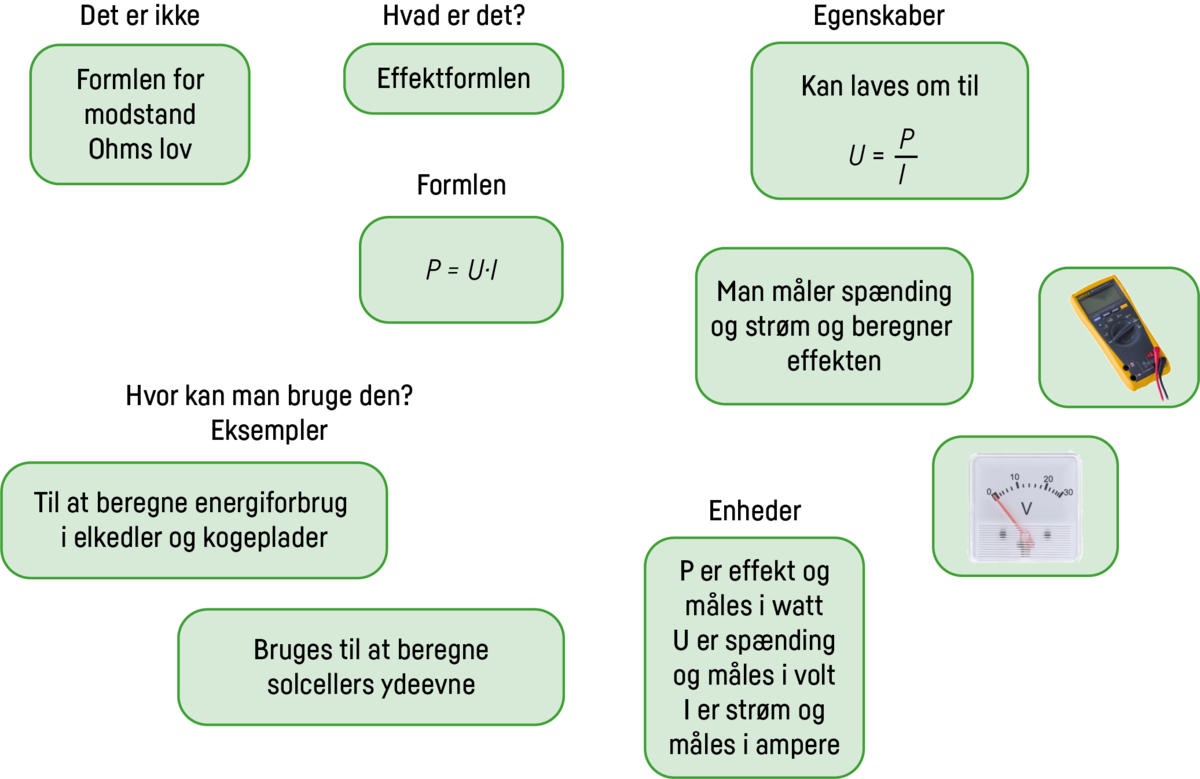
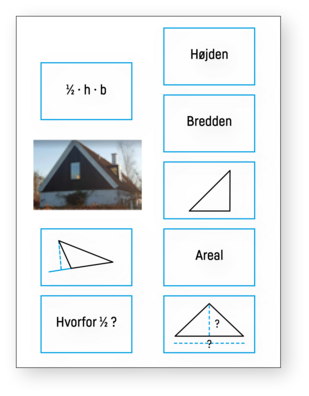
Begrebskort og ordkendskabskort hjælper elever med at blive opmærksomme på nye begrebers betydninger. Det er nødvendigt, at eleverne får lov til at beskrive og forklare begreberne med egne og førfaglige ord, for at de kan opdage forskellene på f.eks. stofmængde, volumen, styrke i en fortynding eller blandingsforhold, volumen og koncentration i en betonmix (Bull & Blankholm, 2021).
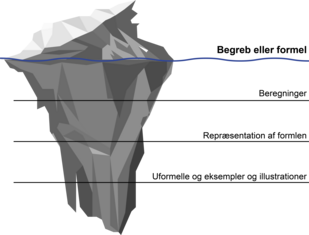
’Isbjergmodellen’ kan bruges til at afdække, hvad der relaterer sig til en formel. Det begreb, som formlen indgår i, kan man tænke på som toppen af isbjerget, der stikker op over havoverfladen. I undervisningen bruger man isbjergmodellen til at samle op og strukturere de associationer og den viden, eleverne har om et givet matematisk begreb, og den eller de formler, som beskriver det. På figuren er begrebet skrevet i den del af isbjerget, der rager op over vandoverfladen. Under vandoverfladen ligger elevernes kendskab og associationer for begrebet, som med lærerens hjælp er organiseret i tre niveauer: Underst er de uformelle situationer, eksempler og anvendte redskaber placeret. I midten ligger repræsentationer for de erfaringer og situationer, eleverne kender; diagrammer, tegninger og grafer. Og øverst lige under ’vandoverfladen’ placeres formler og beregninger.
Begrebskort, ordkendskabskort og isbjergmodellen kan både bruges til formler, som eleverne er blevet introduceret til i grundskolen, og til nye problemstillinger, som eleverne ikke har forudsætninger for at kende på forhånd. Det kan fx være trigonometriske formler, formlen for skærehastighed eller lignende. Begrebskort, ordkendskabskort og isbjergmodellen kan f.eks. bruges på sammenhængen mellem hældning og højde på en stige og på udtryk for og sammenhænge mellem de forskellige elementer i bølgers bevægelse. I afsnittet Praksis er vist et eksempel på en isbjergmodel om ’styrke’ fra sygeplejeuddannelsen.
Sprog i matematikundervisningen
Læreren skal være opmærksom på arbejdet med førfaglige ord til beskrivelse af situationerne.
Førfaglige ord kan defineres som ord, faglærere forudsætter at studerende kender til og kan forklare. Det kan være ord som ’modstand’, ’stejl’, ’øge’, ’positiv’. For en elev med et ringe udviklet sprog eller med dansk som andetsprog kan betydningen af en vending som ’4 går op i 12’ være ukendt og få eleven til at kigge op i loftet med et undrende udtryk. Det kan give problemer, hvis eleverne mangler eller ikke forstår førfaglige ord. De førfaglige ord har en implicit matematisk betydning, mens fagbegreber kan defineres som matematiske begreber med en eksplicit definition, der tit vil være formuleret vha. simplere matematiske begreber.
Derudover har man fagord. Fagord har den fordel, at de er præcist beskrevet og kan formidle præcise budskaber. I denne sammenhæng kan det være Pythagoras' sætning, decimaltal, kvadratmeter, formel, tangens osv. Der skal arbejdes med koblingen mellem førfaglige ord og fagbegreber.
Gennem undersøgelser og italesættelse udvikler eleverne egne forklaringer og begreber, som alle involverede forstår og kan bruge. Herved udvikler eleverne ’efter-faglige’ ord og modeller.
Man skal også være opmærksom på hjemmelavede ord og vendinger. I undervisningen hører man sommetider hjemmelavede ord, begreber, remser eller lignende, der et udtryk for en bestemt forståelse eller en reference til læringsprocessen. Det kan f.eks. være ’at krydsgange’ eller ’at-dividere-med-en-brøk-er-det-samme-som-at-gange-med-den-omvendte’. Den slags remser kan være en del af resultatet af en læreproces, men de må aldrig stå alene.
En anden type vendinger og begreber opstår i klassen og bliver accepteret som matematikrelaterede. Det kan være ’Peters metode’, ’brøkvinklen og decimalvinklen’ (i arbejdet med at lære trigonometri), eller når tallet π omtales som ’rundt-om-tallet’ for cirklen.
Et mål for undervisningen er, at eleverne får indlejret førfaglige ord og fagord i deres aktive ordforråd, og at de er trygge og kompetente i at udvikle egne begreber, som kan understøtte deres tænkning og kommunikation. Undervisningen i dette læringsspor handler om at koble matematikken – nemlig formlerne i formelsamlingen – både til erhvervsfaglige problemer og situationer og til elevernes erfaringer og forforståelser med matematik. Herefter kan formlerne komme i anvendelse til løsning af konkrete problemstillinger. Dette foregår i fire faser med hvert sit fokus:
-
Først afdækkes elevernes forskellige forudsætninger og viden om det konkrete erhvervsfaglige emne og de formler, der knytter sig hertil.
-
Dernæst har undervisningen fokus på at genkende og gøre rede for formlerne og de størrelser og enheder, der indgår i dem.
-
Så undervisning med fokus på forskellige repræsentationer fra erhvervsfagene og matematikken, herunder formlerne og deres sammenhænge. Eventuelt opstilling af simple formler ud fra en anden repræsentation eller kontekst.
-
Til slut en undervisning, hvor formlerne i deres forskellige repræsentationsformer anvendes til problemløsning. Undervejs er der fokus på de forskellige forståelser af formlerne, der er nødvendige for at kunne løse de givne opgaver.
De nævnte aktiviteter kan også bruges til at træne ikke-matematiske førfaglige og faglige ord og begreber fra erhvervsfaget: f.eks. frihøjde, mellemskære, rette af, stik, murskifte, strege op, sværte af, grunde osv.
Faglæreren introducerer og bruger disse ord i sin værkstedsundervisning, men der skal en aktiv indsats til for at få eleverne til at gøre ordene til deres egne og at de skaber deres egen forståelse for ordene, og her kan matematiklæreren være en stor hjælp.