Gode matematikopgaver
Om en matematikopgave er god afhænger naturligvis af elevens og klassens forudsætninger, men i lige så høj grad af læringspotentialet i opgaven. Læs om, hvordan man som lærer kan støtte, at læringspotentialet i opgaverne realiseres for flest mulige elever.
Matematisk aktivitet starter med en opgave – uden opgaver, ingen matematisk aktivitet. Opgaven kan være mere eller mindre 'let' for en given elev, og vi bruger da også typisk opgaver til at evaluere elevers matematiske viden og kunnen (eller kompetence). Handling og formulering kan indskrænke sig til at aktivere paratviden under tidspres – fx ved en eksamen eller test – eller de kan involvere mere avanceret matematisk aktivitet, som udvikler ny viden hos eleverne. En opgave kan også være så bredt formuleret, at den skal præciseres eller omformuleres for at kunne løses.
Se eksempler på dette i Tre slags matematiske opgaver.
Det gælder i høj grad for projektopgaver. Både praktiske og mere teoretiske opgaver kan motivere en kombination af 'opsøgning af viden' (fx i en lærebog, eller på nettet), kommunikation med andre og selvstændige forsøg på at udvikle en løsning med kendte teknikker.
Om en matematikopgave er 'god' i en undervisningsmæssig sammenhæng med en given elevgruppe, afhænger af, hvor meget eleverne kan lære af at arbejde med den. Her er 'meget' selvfølgelig upræcist, men også utilstrækkeligt: Det er normalt ikke ligegyldigt, hvad eleverne lærer. Udbyttet af at arbejde med en given opgave afhænger også af elevernes forkundskaber. Samme opgave kan være god i én sammenhæng og irrelevant i en anden.
Se eksempler på dette i Matematiske aktiviteter
Det er et centralt element ved tilrettelæggelse af undervisning, at man som lærer tager stilling til, hvilke opgaver eleverne skal arbejde med, hvad der er læringspotentialet ved udvalgte opgaver, og hvordan man som lærer kan støtte, at læringspotentialet ved opgaverne realiseres for flest mulige elever.
Læringspotentiale
En opgaves læringspotentiale for en given elevgruppe er den matematiske viden og kunnen, som elevgruppen kan udvikle ved at arbejde med opgaven. Dette potentiale kan ikke bestemmes teoretisk, men må afprøves i praksis. I den forstand er matematikundervisning en eksperimentel aktivitet, hvor opgaven er en central del af hypotesen: Vi stiller en given opgave, fordi vi tror, at eleverne kan lære noget (ofte noget bestemt!) af at løse den.
Kendskab til opgaver, der i en given sammenhæng har højt læringspotentiale, er en helt central del af matematiklærerens viden. Selv erfarne lærere kan selvfølgelig blive overraskede over, hvor meget eller lidt eleverne lærer af en opgave. Det gælder i særlig grad problemopgaver og projektopgaver, hvor læringspotentialet kan være højt, men hvor risikoen for at 'ramme forkert' (fx opgaven viser sig at være for svær) er større. Men at stille sådanne opgaver rummer også langt større muligheder for, at læreren selv lærer noget (fx om hvad eleverne er i stand til), og dermed på sigt for, at eleverne lærer mere.
En opgave om differens af tocifrede tal
Hvordan afhænger udbyttet af arbejdet med en opgave af eleverne og af måden læreren bruger den på?
For at blive klogere på det, vil vi se på et eksempel fra praksis. Lektionen, som blev gennemført med en 4.-klasse, handlede om én opgave. (Det stammer fra en "offentlig lektion" gennemført af den japanske matematiklærer Hiroshi Tanaka på en skole i Lyngby-Taarbæk Kommune den 24. november 2015. (Kilde 1)).
Vi giver først en formulering af opgaven for voksne:
(*) Tag to cifre, og skriv to tal med dem. Hvad kan du sige om differencen af tallene?
Denne formulering af opgaven er selvfølgelig for abstrakt for en 4.-klasse. Vi forenkler lidt, hvad der faktisk blev gjort i den omtalte lektion. Opgaven 'stilles' på flg. måde:
En elev bliver (foran hele klassen) præsenteret for 10 kort, der hver viser ét af cifrene 0,1,2, … ,9, og skal så vælge to af kortene – fx 2 og 7.
Læreren spørger nu: Hvilke tal kan vi skrive med 2 og 7?
Eleven svarer straks: 27 og 72.
Hvilket af tallene er størst?
Svaret kommer umiddelbart: 72.
Hvad sker der, når vi trækker det mindste tal fra det største?
Dette er en typeopgave for eleverne, som med større eller mindre lethed svarer: 45.
På tavlen skrives:

Læreren hæfter sig ikke særligt ved resultatet, men kalder en anden elev op og beder om det samme. Eleven vælger 2 og 4, og på tavlen skrives:
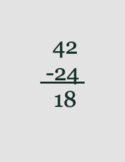
Sådan fortsættes en tid, og flere regnestykker af ovenstående type kommer på tavlen; læreren skriver dem pænt op ved siden af hinanden. På denne måde involveres eleverne i handlinger, som er relevante for opgaven (*), uden denne er formuleret i sin abstrakte form. Læreren stiller efter et (efter hans vurdering, passende) antal handlinger spørgsmålet: "Lægger i mærke til noget?" Eleverne bliver bedt om at tale med sidemanden, og skrive forslag ned. Læreren går rundt mellem bordene og iagttager, hvad de skriver. Når alle har skrevet noget, beder han udvalgte elever om at sige (til hele klassen), hvad de har skrevet ned.
To hypoteser går igen:
- Resultatet (under stregen) er et tal i 9-tabellen
- Resultatet er det tal i 9-tabellen, som fås ved at gange differencen mellem cifrene med 9.
Særlig det sidste er svært at formulere og forstå. Men til sidst har vi disse to formuleringer, som valideres ved at se på flere af eksemplerne på tavlen. Her ender lektionen – ovenstående tog faktisk 45 minutter at gennemføre i en 4.-klasse.
Vi lægger mærke til to ting:
- At arbejdet med en problemopgave sagtens kan omfatte løsning af adskillige typeopgaver. Her drejer det sig om subtraktioner af tal, som er udfordrende for mange elever: Cifrene kan ikke bare trækkes fra hinanden hver for sig – i hvert fald gør ingen elever det.
- Arbejdet med regneeksemplerne giver mulighed for at sammenligne forskellige regnemetoder; så det er en del af opgavens læringspotentiale. Men den centrale udfordring i (*) er at formulere og validere en hypotese, som for eleverne er både overraskende og lidt svær at forholde sig til. Valideringen er i den beskrevne lektion kun induktiv, dvs. man slutter noget generelt fra konkrete eksempler. Passer det i alle eksempler, vi kan finde på, tror vi på hypotesen.
Men man kunne – selv i en 4.-klasse – også gå videre ved at se nærmere på hvordan subtraktionerne foretages. Måske kan nogle elever, evt. med hjælp fra læreren, formulere forklaringer, der tager udgangspunkt i konkrete regnemetoder, fx:
$72 − 27 = 70 + 2 − 20 − 7 = 70 − 20 − 5 = 5 ⋅ 10 − 5 = 5 ⋅ 9$
Mere generelt: hvis man skriver de to tal op vha. 'tiere' og 'enere' og håndterer dem hver for sig, så ser vi, at forskellen (her $5$) af sig selv dukker op to gange – nemlig dels som $5⋅10$, dels som noget, der skal trækkes fra ($5$). Selv uden parentesregning (mere præcist, den distributive lov: $5⋅10−5=5⋅(10−1)$) kan eleverne måske se, at resultatet altid bliver cifrenes differens ganget med 9. Læreren kan institutionalisere sådanne forklaringer med eller uden input fra eleverne – uden elevbidrag kan det dog være mere tvivlsomt, hvad eleverne får ud af det.
Opgaven har altså, for så vidt angår valideringen, stort læringspotentiale, som afhængigt af elevernes forudsætninger kan realiseres på forskellige måder. Samme opgave har været brugt i gymnasial undervisning. (Kilde 2)
Eleverne lykkes på forskellig måde med at validere hypotesen ved at opstille og bruge en algebraisk model:
$(10a + b) − (10b + a) = 9 (a−b)$
hvor $a, b ∈$ {$0,1,..,9$} og $a > b$. Her er læringspotentialet altså hovedsageligt algebraisk modellering af et aritmetisk fænomen, som fører til et generelt bevis. Også i andre sammenhænge, fx i erhvervsuddannelsernes arbejde med positionssystemer, kunne opgaven være relevant. Den har, som de fleste problemopgaver, også mere eller mindre oplagte varianter, fx med tal, der har flere cifre end to.
Se tema om Positionssystemer til erhvervsuddannelserne.
Eksemplet illustrerer en vigtig pointe: Realiseringen af en opgaves læringspotentiale afhænger ikke kun af opgaven og elevgruppen. Det afhænger også af, hvordan den 'bruges' i undervisningen – mere præcist: hvad læreren gør for at 'styre' (fx igangsætte) de forskellige dele af elevernes matematiske aktivitet.
Læs også:
- de fem typer af situationer, hvor læreren 'styrer' aktiviteterne i Situationer i matematikundervisningen
- strukturen i ovenstående eksempel som lektionsplan i To slags matematikundervisning
TIL OVERVEJELSE I FAGTEAMET
-
Hvor henter jeg normalt (idéer til) opgavemateriale? (Jf. idéerne ovenfor)
-
Hvordan bedømmer jeg relevansen af opgavematerialet for de elever og det undervisningsmæssige indhold, jeg arbejder med nu?
-
Hvordan kan jeg sparre med kolleger om brug og udvikling af opgaver i min egen undervisning – her og nu, og måske på længere sigt?
-
Hvordan finder jeg en balance mellem den nødvendige træning af basale matematiske teknikker, og nødvendigheden af at udvikle mine elevers kritiske og selvstændige stillingtagen til egne og andres løsninger?
-
Har jeg et arsenal af opgaver, som kan bruges til lejlighedsvis undervisning efter strukturen som eksemplificeres i Tabel 3?
Hvordan kan dette 'arsenal' (videre)udvikles, jf. spørgsmål 1-3 ovenfor?
til: GRUNDSKOLE, ERHVERVSSKOLE, GYMNASIE
emne: UNDERVISNINGSPLANLÆGNING
UDGIVET: 2022
Forfatter
Carl Winsløw
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Lauritsen, H. (2015). Japansk inspiration til matematik. Folkeskolen (5. nov. 2015).
- Winsløw, C. (2019). Undersøgelsesbaseret matematikundervisning. Lokaliseret 01.11.21 på: https://emu.dk/sites/default/files/2020-12/MERIA-bogen.pdf s. 27-29